Geometry Section 9 7 EXAMPLE 1 Identify dilations

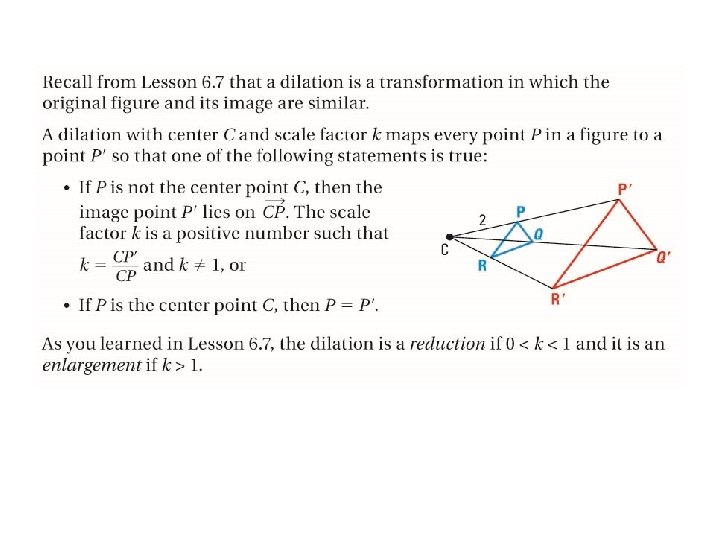
Geometry Section 9. 7

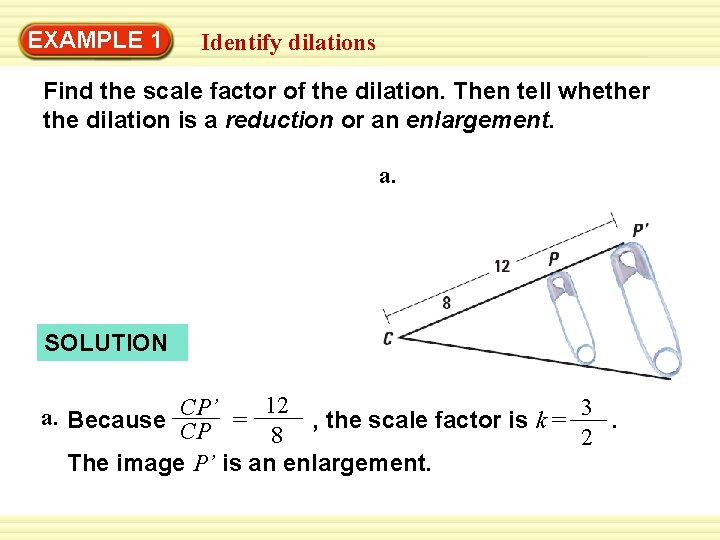
EXAMPLE 1 Identify dilations Find the scale factor of the dilation. Then tell whether the dilation is a reduction or an enlargement. a. SOLUTION a. Because CP’ = 12 , the scale factor is k = 3. CP 8 2 The image P’ is an enlargement.

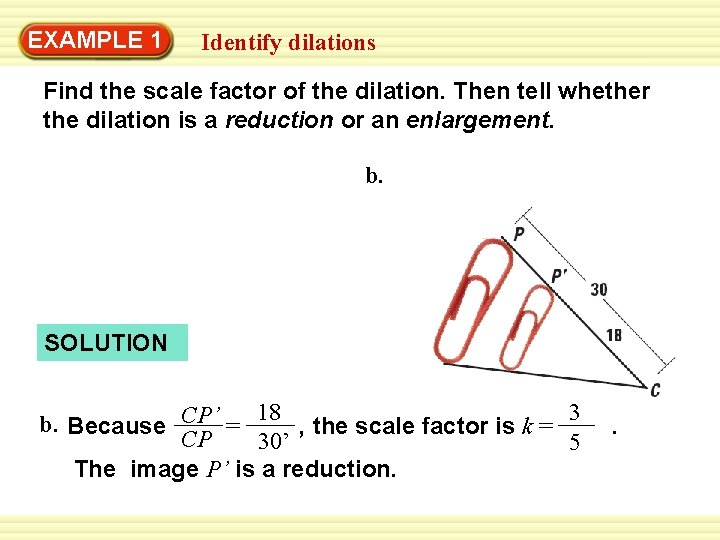
EXAMPLE 1 Identify dilations Find the scale factor of the dilation. Then tell whether the dilation is a reduction or an enlargement. b. SOLUTION b. Because CP’ = 18 , the scale factor is k = 3 CP 30’ 5 The image P’ is a reduction. .

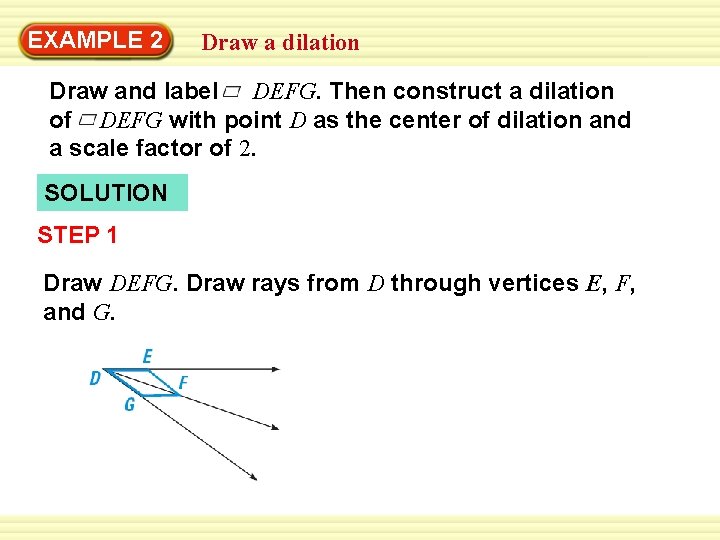
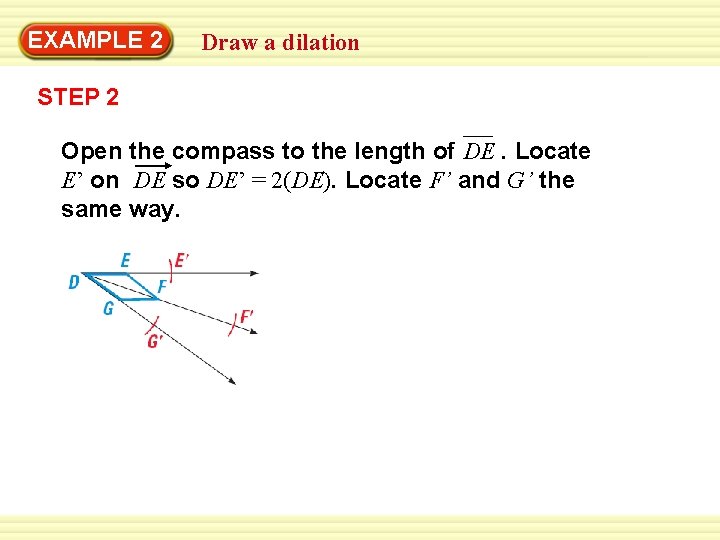
EXAMPLE 2 Draw a dilation Draw and label DEFG. Then construct a dilation of DEFG with point D as the center of dilation and a scale factor of 2. SOLUTION STEP 1 Draw DEFG. Draw rays from D through vertices E, F, and G.

EXAMPLE 2 Draw a dilation STEP 2 Open the compass to the length of DE. Locate E’ on DE so DE’ = 2(DE). Locate F’ and G’ the same way.

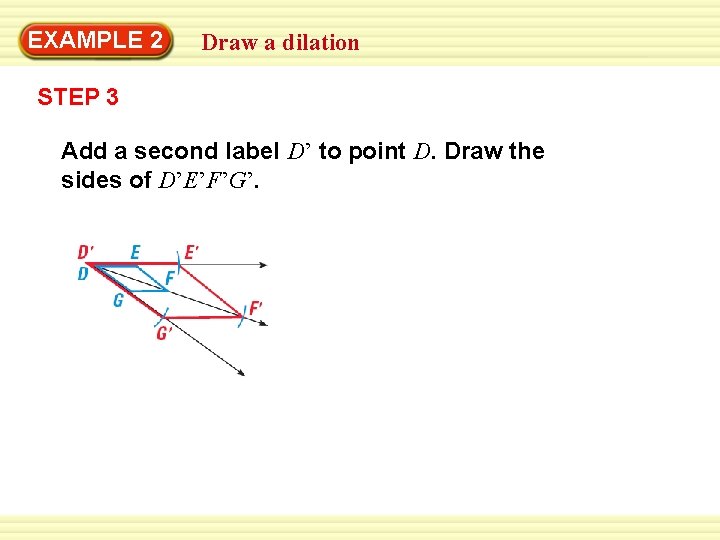
EXAMPLE 2 Draw a dilation STEP 3 Add a second label D’ to point D. Draw the sides of D’E’F’G’.

Assignment 1 of 2 • #3 -13 odd, page 629

EXAMPLE 3 Scalar multiplication [ Simplify the product: 4 3 0 1 2 – 1 – 3 ] SOLUTION [ 4 3 0 1 2 – 1 – 3 ][ [ = = 4(3) 4(0) 4(1) ] 4(2) 4(– 1) 4(– 3) 12 0 ] 4 8 – 4 – 12 Multiply each element in the matrix by 4. Simplify.

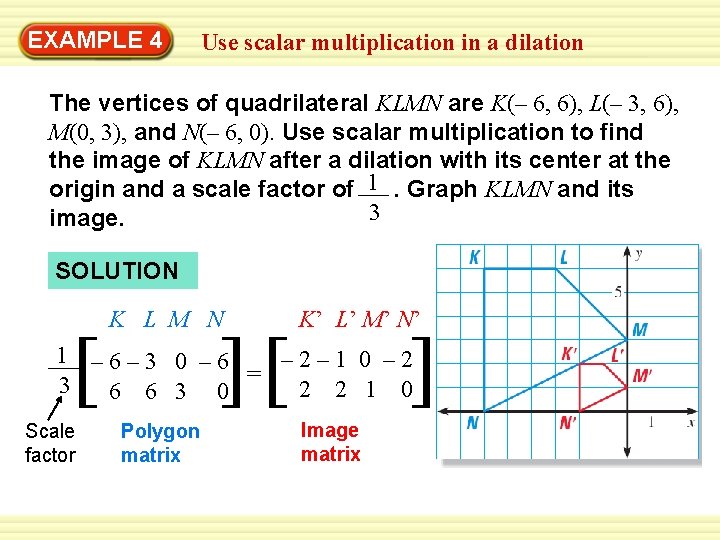
EXAMPLE 4 Use scalar multiplication in a dilation The vertices of quadrilateral KLMN are K(– 6, 6), L(– 3, 6), M(0, 3), and N(– 6, 0). Use scalar multiplication to find the image of KLMN after a dilation with its center at the origin and a scale factor of 1. Graph KLMN and its 3 image. SOLUTION [ K L M N ][ K’ L’ M’ N’ ] 1 – 6– 3 0 – 6 – 2– 1 0 – 2 = 3 2 2 1 0 6 6 3 0 Scale factor Polygon matrix Image matrix

EXAMPLE 5 Find the image of a composition The vertices of ABC are A(– 4, 1), B(– 2, 2), and C( – 2, 1). Find the image of ABC after the given composition. Translation: (x, y) (x + 5, y + 1) Dilation: centered at the origin with a scale factor of 2 SOLUTION STEP 1 Graph the preimage ABC on the coordinate plane.

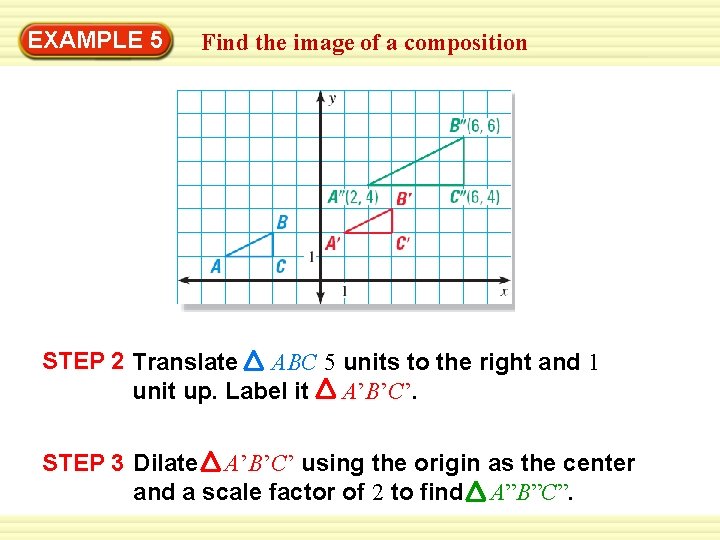
EXAMPLE 5 Find the image of a composition STEP 2 Translate ABC 5 units to the right and 1 unit up. Label it A’B’C’. STEP 3 Dilate A’B’C’ using the origin as the center and a scale factor of 2 to find A”B”C”.

Assignment 2 of 2 • #15 -25 odd, pages 629 & 630