Geometry Section 10 1 EXAMPLE 1 Identify special

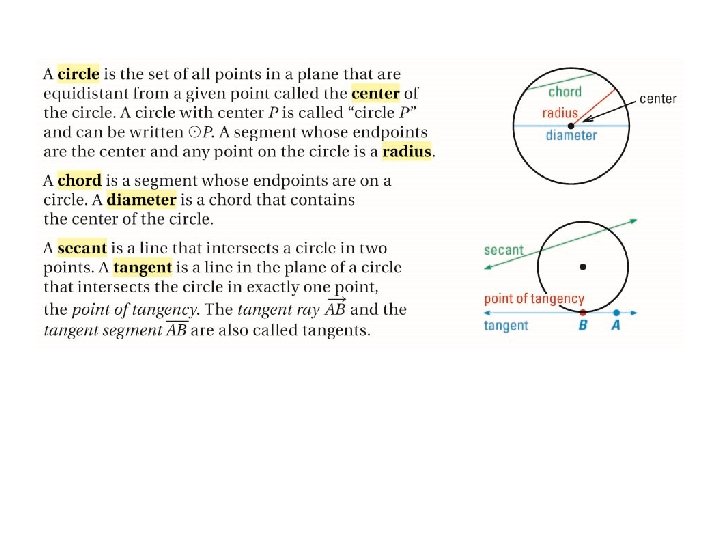
Geometry Section 10. 1

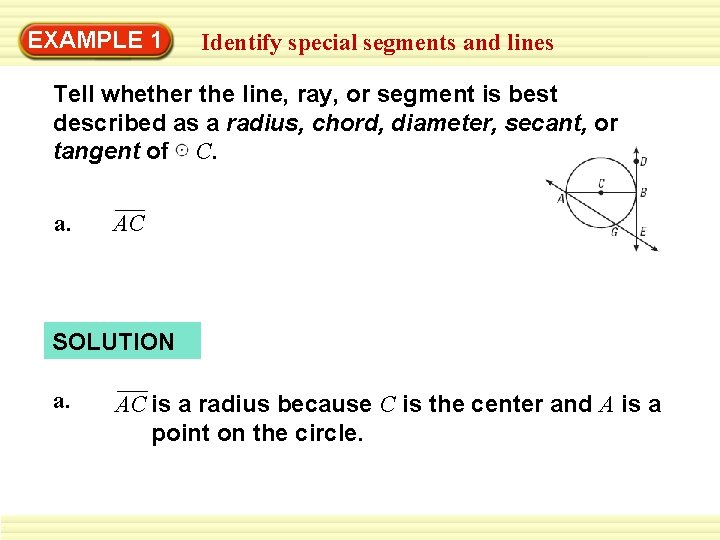
EXAMPLE 1 Identify special segments and lines Tell whether the line, ray, or segment is best described as a radius, chord, diameter, secant, or tangent of C. a. AC SOLUTION a. AC is a radius because C is the center and A is a point on the circle.

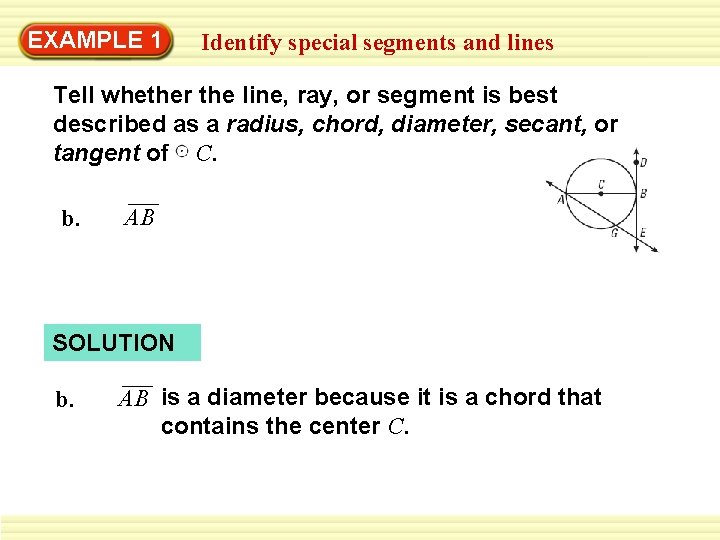
EXAMPLE 1 Identify special segments and lines Tell whether the line, ray, or segment is best described as a radius, chord, diameter, secant, or tangent of C. b. AB SOLUTION b. AB is a diameter because it is a chord that contains the center C.

EXAMPLE 1 Identify special segments and lines Tell whether the line, ray, or segment is best described as a radius, chord, diameter, secant, or tangent of C. c. DE SOLUTION c. DE is a tangent ray because it is contained in a line that intersects the circle at only one point.

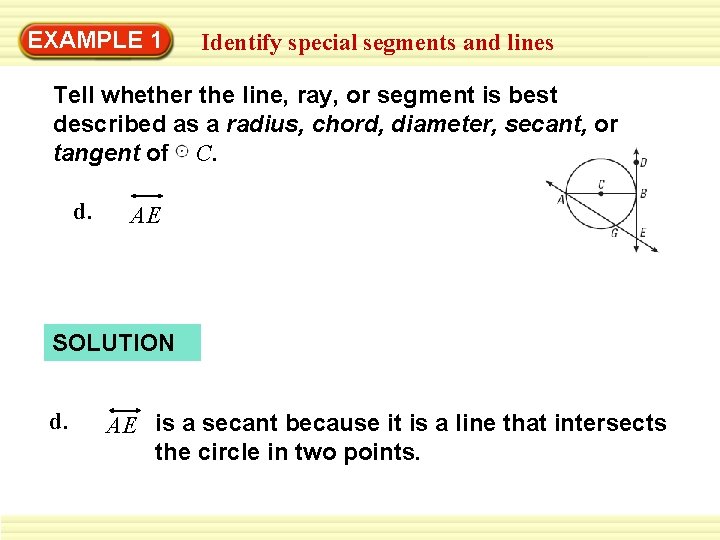
EXAMPLE 1 Identify special segments and lines Tell whether the line, ray, or segment is best described as a radius, chord, diameter, secant, or tangent of C. d. AE SOLUTION d. AE is a secant because it is a line that intersects the circle in two points.

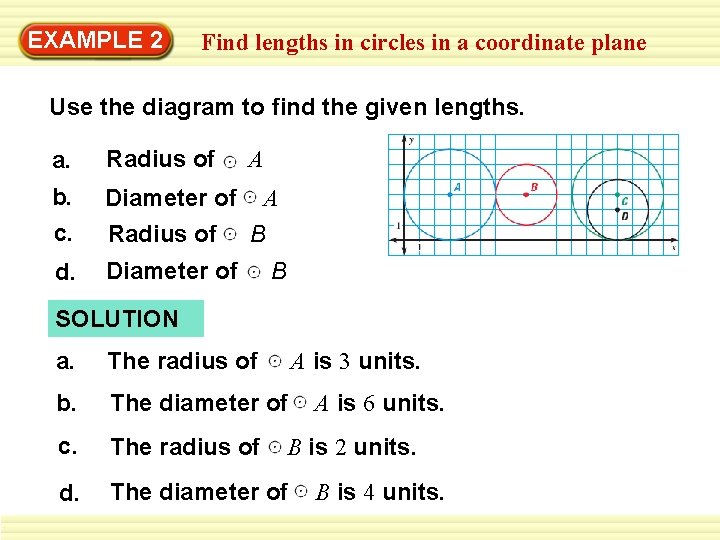
EXAMPLE 2 Find lengths in circles in a coordinate plane Use the diagram to find the given lengths. a. Radius of b. c. Diameter of d. Diameter of Radius of A A B B SOLUTION a. The radius of A is 3 units. b. The diameter of c. The radius of d. The diameter of A is 6 units. B is 2 units. B is 4 units.

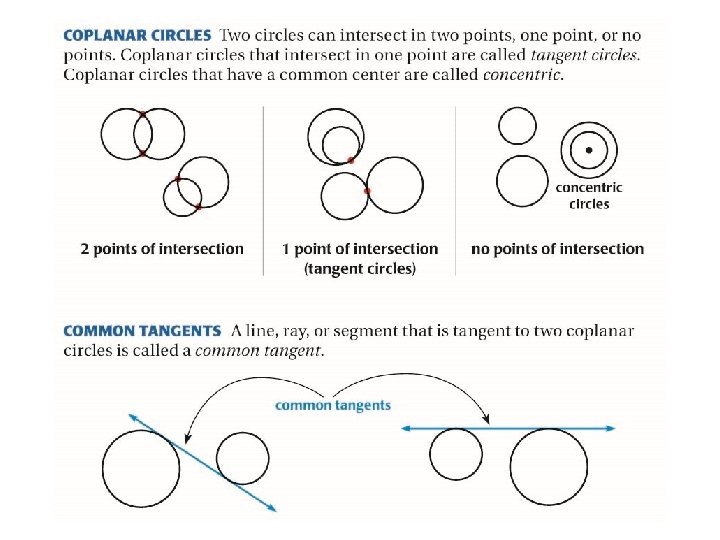
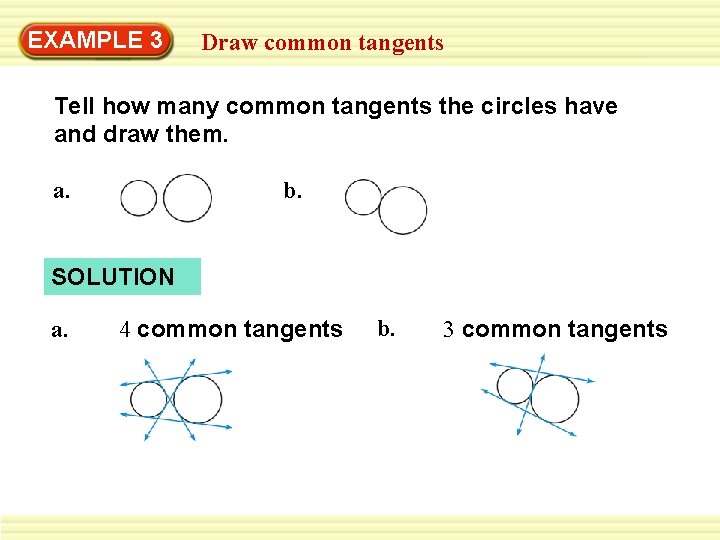
EXAMPLE 3 Draw common tangents Tell how many common tangents the circles have and draw them. a. b. SOLUTION a. 4 common tangents b. 3 common tangents

EXAMPLE 3 Draw common tangents Tell how many common tangents the circles have and draw them. c. SOLUTION c. 2 common tangents

Assignment 1 of 2 • #3 -10 all, 13 -17 odd, page 655

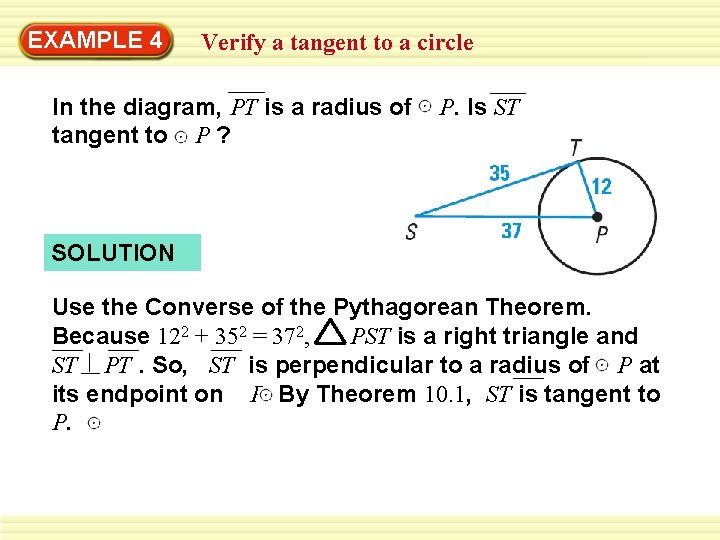
EXAMPLE 4 Verify a tangent to a circle In the diagram, PT is a radius of tangent to P ? P. Is ST SOLUTION Use the Converse of the Pythagorean Theorem. Because 122 + 352 = 372, PST is a right triangle and ST PT. So, ST is perpendicular to a radius of P at its endpoint on P. By Theorem 10. 1, ST is tangent to P.

EXAMPLE 5 Find the radius of a circle In the diagram, B is a point of tangency. Find the radius r of C. SOLUTION You know from Theorem 10. 1 that AB BC , so ABC is a right triangle. You can use the Pythagorean Theorem. AC 2 = BC 2 + AB 2 Pythagorean Theorem (r + 50)2 = r 2 + 802 r 2 + 100 r + 2500 = r 2 + 6400 100 r = 3900 r = 39 ft. Substitute. Multiply. Subtract from each side. Divide each side by 100.

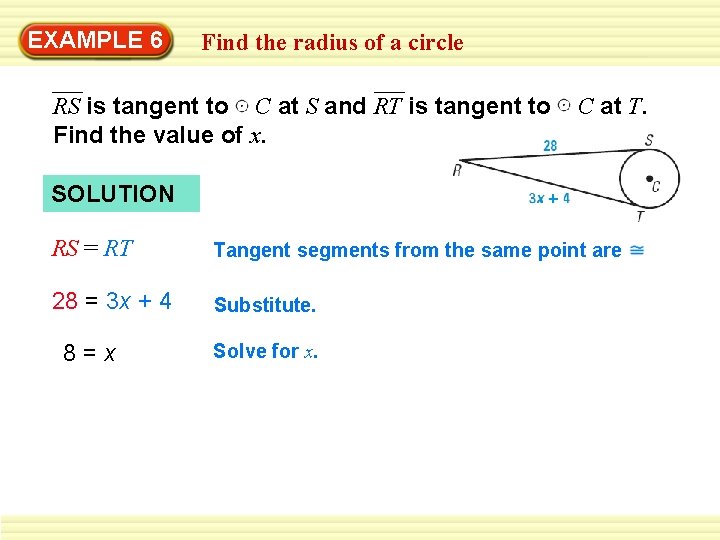
EXAMPLE 6 Find the radius of a circle RS is tangent to C at S and RT is tangent to Find the value of x. C at T. SOLUTION RS = RT Tangent segments from the same point are 28 = 3 x + 4 Substitute. 8=x Solve for x.

Assignment 2 of 2 • #19 -25 odd, page 656