Geometry Many slides adapted from Octavia Camps and

Geometry (Many slides adapted from Octavia Camps and Amitabh Varshney)

Goals • Represent points, lines and triangles as column vectors. • Represent motion as matrices. • Move geometric objects with matrix multiplication. • Refresh memory about geometry and linear algebra

Vectors • Ordered set of numbers: (1, 2, 3, 4) • Example: (x, y, z) coordinates of pt in space.

Vector Addition v V+w w

Scalar Product av v

Inner (dot) Product v w The inner product is a SCALAR!

Points Using these facts, we can represent points. Note: (x, y, z) = x(1, 0, 0) + y(0, 1, 0) + z(0, 0, 1) x = (x, y, z). (1, 0, 0) z = (x, y, z). (0, 0, 1) y = (x, y, z). (0, 1, 0)

Lines • Line: y = mx + a `d • Line: sum of a point and a vector P = P 1 + `d (where`d is a column vector) P 1 P 2 • Line: Affine sum of two points P = 1 P 1 + 2 P 2, where 1 + 2 = 1 P 1 Line Segment: For 0 £ 1, 2 £ 1, P lies between P 1 and P 2 • Line: set of points equidistant from the origin in the direction of a unit vector.

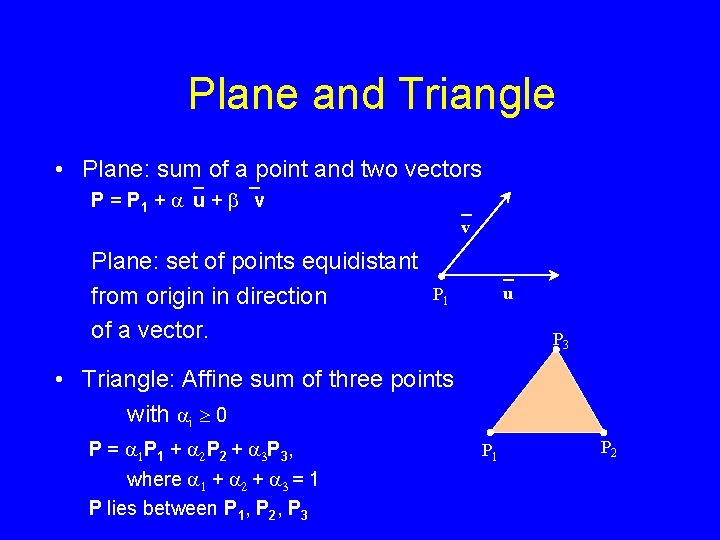
Plane and Triangle • Plane: sum of a point and two vectors P = P 1 + `u + b` v Plane: set of points equidistant from origin in direction of a vector. `v P 1 `u P 3 • Triangle: Affine sum of three points with i ³ 0 P = 1 P 1 + 2 P 2 + 3 P 3 , where 1 + 2 + 3 = 1 P lies between P 1, P 2, P 3 P 1 P 2

Generalizing. . . Affine Sum of arbitrary number of points: Convex Hull P = 1 P 1 + 2 P 2 + … + n. Pn, where 1 + 2 + … + n = 1 and i ³ 0

Normal of a Plane: sum of a point and two vectors P = P 1 + `u + b`v P - P 1 = `u + b`v `v P 1 `u If`n is orthogonal to`u and`v (n =`u ´`v ) : T T T `n · (P - P 1) = `n ·`u + b`n ·`v = 0`n `v P 1 `u

Implicit Equation of a Plane T `n · (P - P 1) = 0 a x x 1 Let`n = b P= y P 1 = y 1 c z z 1 Then, the equation of a plane becomes: a (x - x 1) + b (y - y 1) + c (z - z 1) = 0 `v P 1 `u `n ax+by+cz+d=0 `v P 1 `u Thus, the coefficients of x, y, z in a plane equation define the normal.

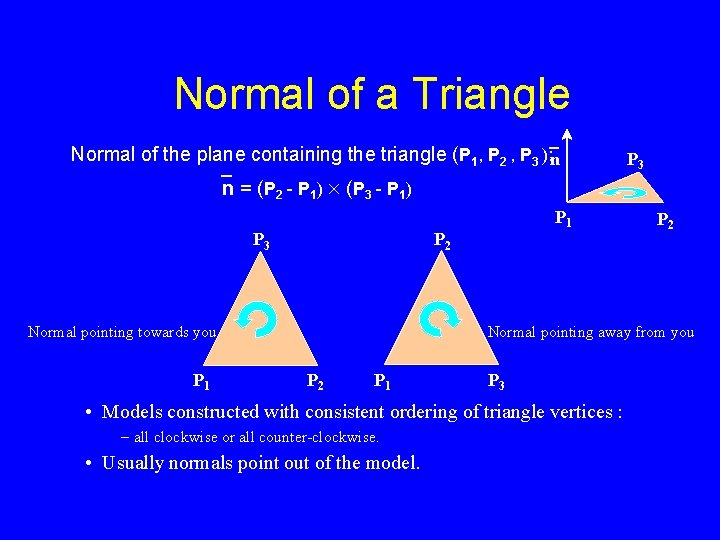
Normal of a Triangle Normal of the plane containing the triangle (P 1, P 2 , P 3 `n ): `n = (P 2 - P 1) ´ (P 3 - P 1) P 3 P 2 Normal pointing towards you P 1 P 3 P 2 Normal pointing away from you P 2 P 1 P 3 • Models constructed with consistent ordering of triangle vertices : - all clockwise or all counter-clockwise. • Usually normals point out of the model.

Normal of a Vertex in a Mesh `nv = (`n 1 +`n 2 + … +`nk) / k = å`ni / k = average of adjacent triangle normals • `nv • `nk or better: `nv = å (Ai `ni) / (k å (Ai) ) = area-weighted average of adjacent triangle normals • `n 3 • `n 1 • `n 2

Geometry Continued • Much of last classes’ material in Appendix A

Matrices Sum: A and B must have the same dimensions

Matrices Product: Identity Matrix: A and B must have compatible dimensions

Matrices • Associative T*(U*(V*p)) = (T*U*V)*p • Distributive T*(u+v) = T*v + T*v

Matrices Transpose: If A is symmetric

Matrices Determinant: A must be square

Euclidean transformations

2 D Translation P’ t P

2 D Translation Equation ty P P’ t y x tx

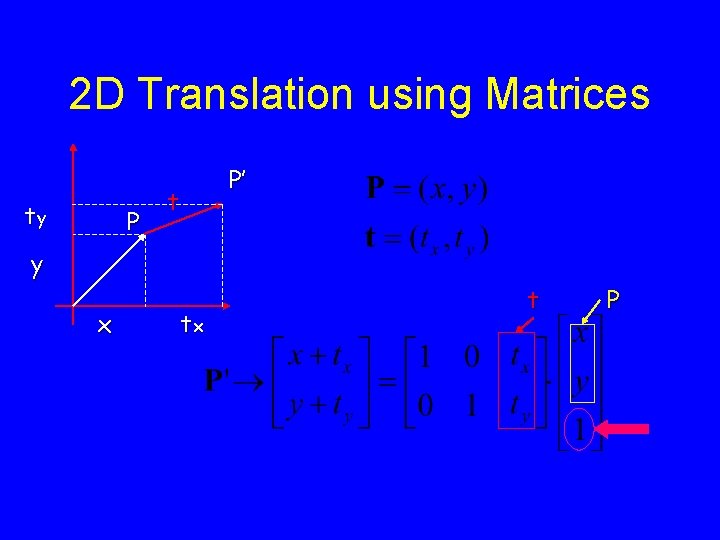
2 D Translation using Matrices ty P P’ t y x tx t P

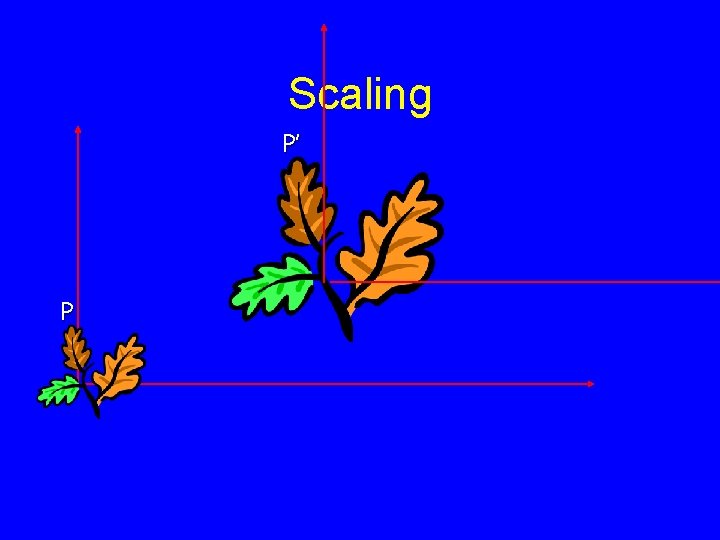
Scaling P’ P

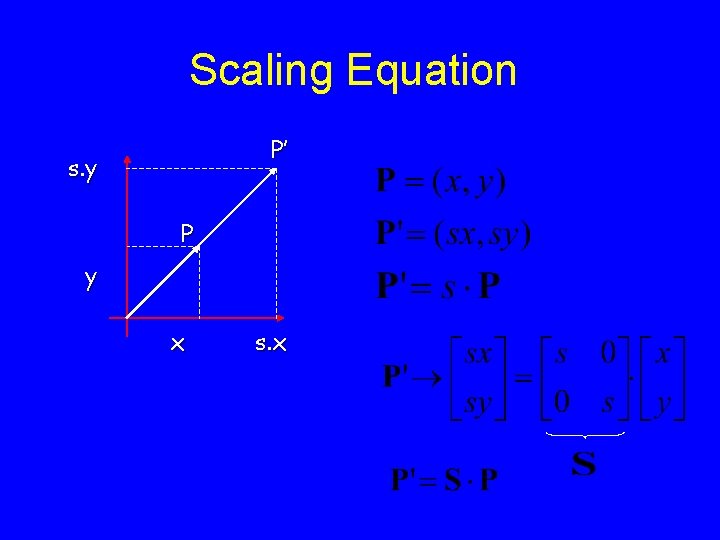
Scaling Equation P’ s. y P y x s. x

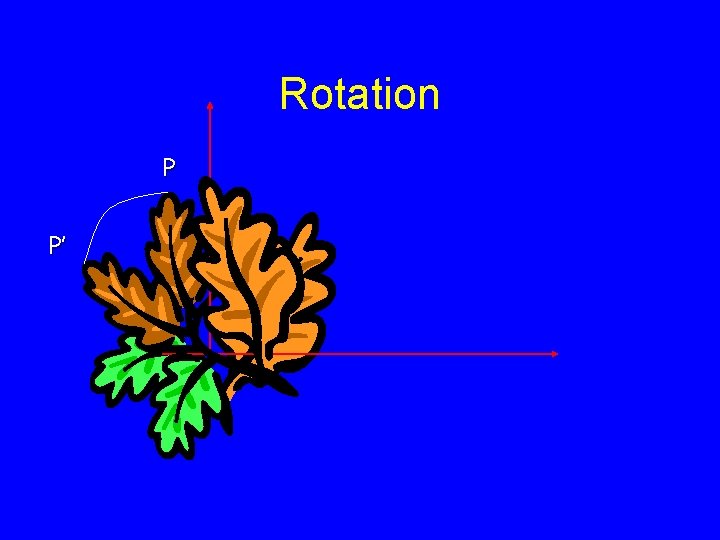
Rotation P P’

Rotation Equations Counter-clockwise rotation by an angle Y’ P’ P y X’ x

Degrees of Freedom R is 2 x 2 4 elements BUT! There is only 1 degree of freedom: The 4 elements must satisfy the following constraints:

Transformations can be composed • Matrix multiplication is associative. • Combine series of transformations into one matrix. (example, whiteboard). • In general, the order matters. (example, whiteboard). • 2 D Rotations can be interchanged. Why?

Rotation and Translation ( cos -sin tx sin cos ty 0 0 )( ) x y 1 1 Rotation, Scaling and Translation ( a -b tx b a ty 0 0 1 )( ) x y 1

Rotation about an arbitrary point • Can translate to origin, rotate, translate back. (example, whiteboard). • This is also rotation with one translation. – Intuitively, amount of rotation is same either way. – But a translation is added.

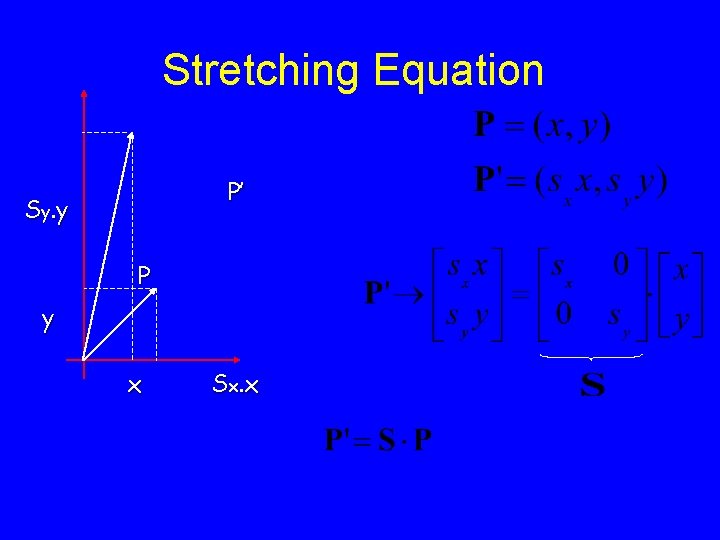
Stretching Equation P’ Sy. y P y x Sx. x

Linear Transformation SVD

Affine Transformation

Viewing Position • Express world in new coordinate system. • If origins same, this is done by taking inner product with new coordinates. • Otherwise, we must translate.

Simple 3 D Rotation about z axis. Rotates x, y coordinates. Leaves z coordinates fixed.

Full 3 D Rotation • Any rotation can be expressed as combination of three rotations about three axes. • Rows (and columns) of R are orthonormal vectors. • R has determinant 1 (not -1).

3 D Rotation + Translation • Just like 2 D case

3 D Viewing Position • Rows of rotation matrix correspond to new coordinate axis.

Rotation about a known axis • Suppose we want to rotate about u. • Find R so that u will be the new z axis. – u is third row of R. – Second row is anything orthogonal to u. – Third row is cross-product of first two. – Make sure matrix has determinant 1.