Geometry Lesson 5 2 Use perpendicular bisectors Learning

Geometry Lesson 5 -2 Use perpendicular bisectors

Learning Target • You will use perpendicular bisectors to solve problems.

Do we remember? ? • Do we remember what the word perpendicular means? • Do we remember what the word bisect or bisector means? • We will put them together to get a line that is cut in half and a right angle.

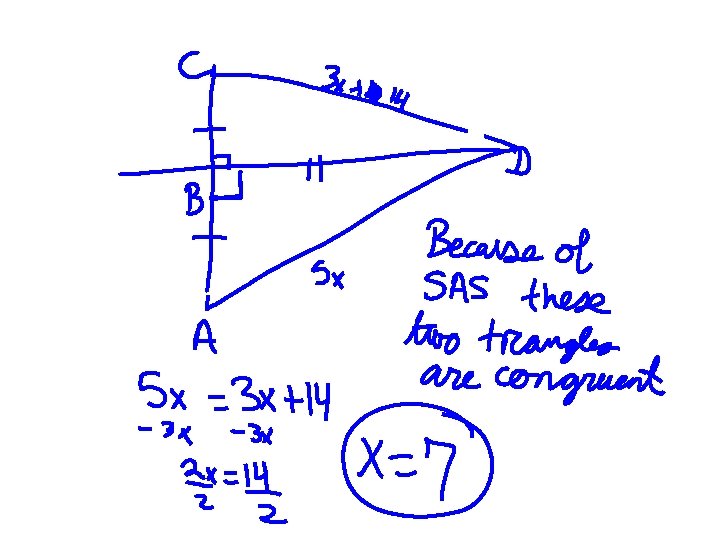
Perpendicular bisectors and angle bisectors • Perpendicular bisector: A perpendicular bisector of a triangle is a line, segment, or ray that passes through the midpoint of the side and is perpendicular to the side. • Theorem 5. 2: If AB is the perpendicular bisector of CD, then AC is congruent to AD. A C B D E • Theorem 5. 3: If CE = ED, then E lies on the perpendicular bisector of CD.

LOOK AT PAGE 303 EXAMPLE 1 • WHAT DOES PERPENDICULAR BISECTOR MEAN? • SO WHAT DOES THAT MEAN ABOUT CD AND AD? • SO HOW DO WE SOLVE THIS? • TRY PAGE 304 GUIDED PRACTICE #1 -2

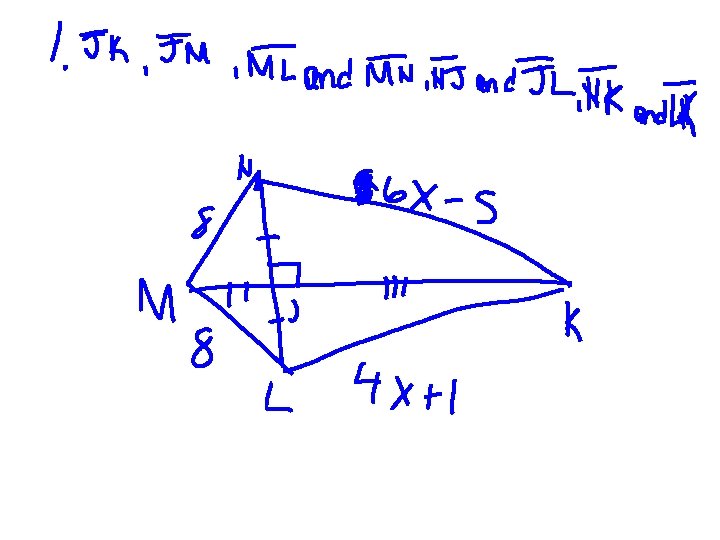
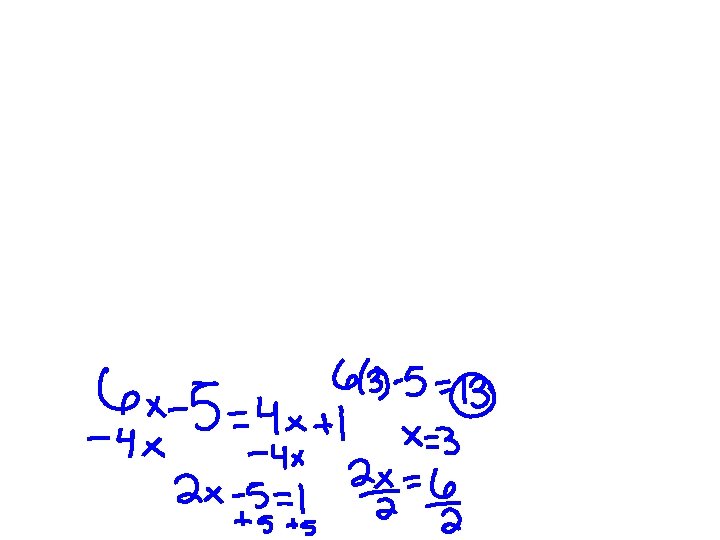
Perpendicular bisectors and angle bisectors (cont’d) • Concurrent Lines: Three or more lines that intersect at a common point. • Point of concurrency: point of intersection of concurrent lines. • Circumcenter: The point of concurrency of the perpendicular bisectors of a triangle.

Concurrency of perpendicular bisectors of a triangle • Says the perpendicular bisectors of a triangle intersect at a point that is equidistant from the vertices of the triangle. – We will draw this picture

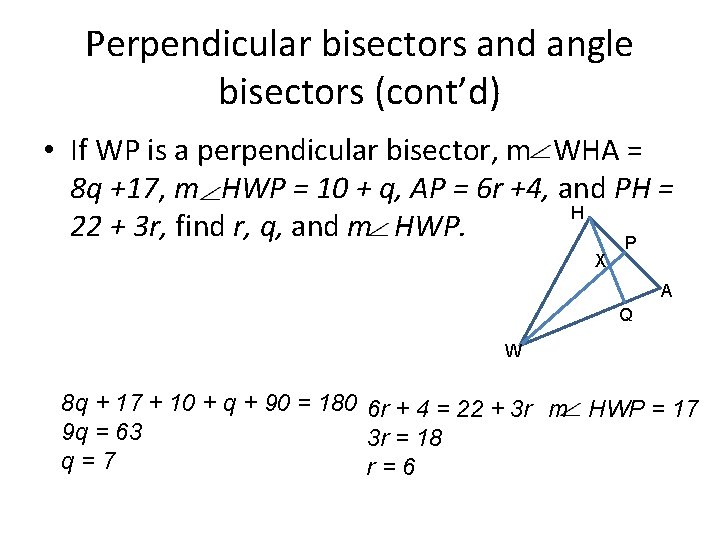
Perpendicular bisectors and angle bisectors (cont’d) • If WP is a perpendicular bisector, m WHA = 8 q +17, m HWP = 10 + q, AP = 6 r +4, and PH = H 22 + 3 r, find r, q, and m HWP. P X A Q W 8 q + 17 + 10 + q + 90 = 180 6 r + 4 = 22 + 3 r m HWP = 17 9 q = 63 3 r = 18 q=7 r=6

Circumcenters • Acute triangles: it is in the triangle • Obtuse: it is outside of the triangle • Right: it is on the triangle

Together • Page 306 # 3, 11, 13, 17, 20

Homework • Page 306 -307 # 4 -16 even