Geometry Lesson 2 8 Proving Angle Relationships Objective

Geometry Lesson 2 – 8 Proving Angle Relationships Objective: Write proofs involving supplementary angles. Write proofs involving congruent and right angles.

Postulate 2. 10 Protractor Postulate l Given any angle, the measure can be put into one-to-one correspondence with real numbers between 0 and 180.

Postulate 2. 11 Angle Addition Postulate

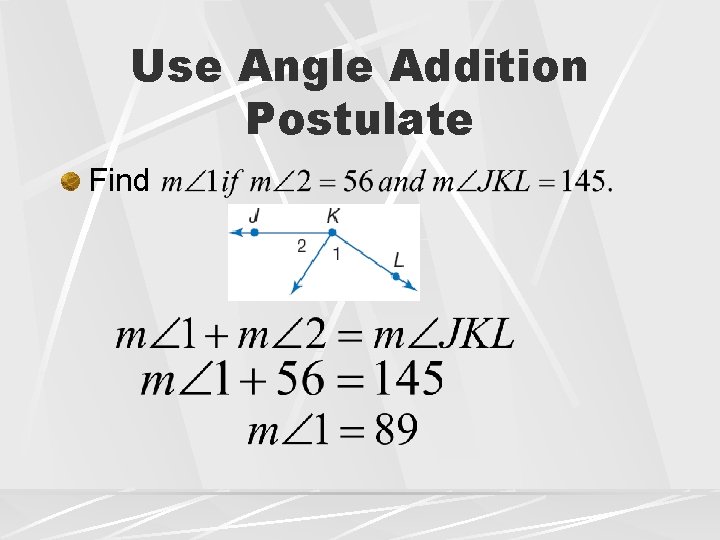
Use Angle Addition Postulate Find

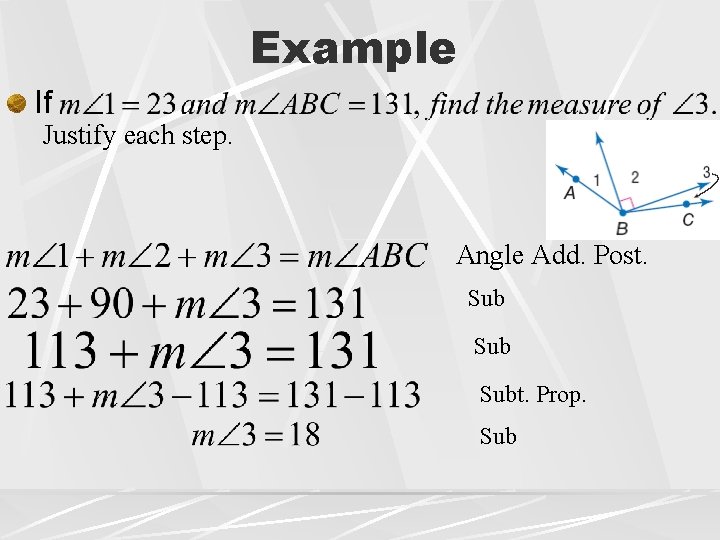
Example If Justify each step. Angle Add. Post. Sub Subt. Prop. Sub

Theorems Supplement Theorem l If two angles form a linear pair, then they are supplementary angles. Complement Theorem l If the noncommon sides of two adjacent angles form a right angle, then the angles are complementary angles.

Example Angles 6 & 7 form a linear pair. Justify each step. Supplement Thm. 3 x + 32 + 5 x + 12 = 180 8 x + 44 - 44 = 180 - 44 8 x = 136 Sub Subt. Prop. Sub Division Prop. x = 17 Sub

Properties of Angle Congruence Reflexive l Symmetric l Transitive l

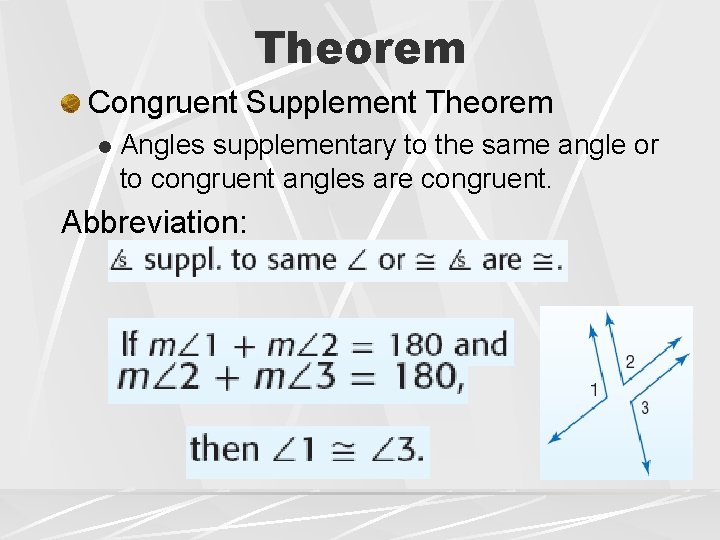
Theorem Congruent Supplement Theorem l Angles supplementary to the same angle or to congruent angles are congruent. Abbreviation:

Theorem Congruent Complements Theorem l Angles complementary to the same angle or congruent angles are congruent. Abbreviation

Prove that the vertical angles 2 and 4 are congruent. Given: Prove:

Theorem 2. 8 Vertical Angle Theorem l If two angles are vertical angles, then they are congruent.

Prove that if DB bisects

Right Angle Theorems Theorem 2. 9 l Perpendicular lines intersect to form 4 right angles Theorem 2. 10 l All right angles are congruent. Theorem 2. 11 l Perpendicular lines from congruent adjacent angles.

Theorem 2. 12 l If two angles are congruent and supplementary, then each angle is a right angle. Theorem 2. 13 l If two congruent angles form a linear pair, then they are right angles.

Homework Pg. 154 1 – 4 all, 6, 8 – 14, 45 - 48 all