Geometry II Further Theorems Solutions Practice Questions 11

  • Slides: 13
Download presentation
Geometry II: Further Theorems Solutions: Practice Questions 11. 2 CHAPTER 11

Geometry II: Further Theorems Solutions: Practice Questions 11. 2 CHAPTER 11

11 1. (i) Practice Questions 11. 2 What more do you need to know

11 1. (i) Practice Questions 11. 2 What more do you need to know in the diagram on the right in order to prove congruency by: ASA? | BAC| = | ACD| (ii) SAS? |AD| = |BC|

11 2. Practice Questions 11. 2 From the information in the diagram, can you

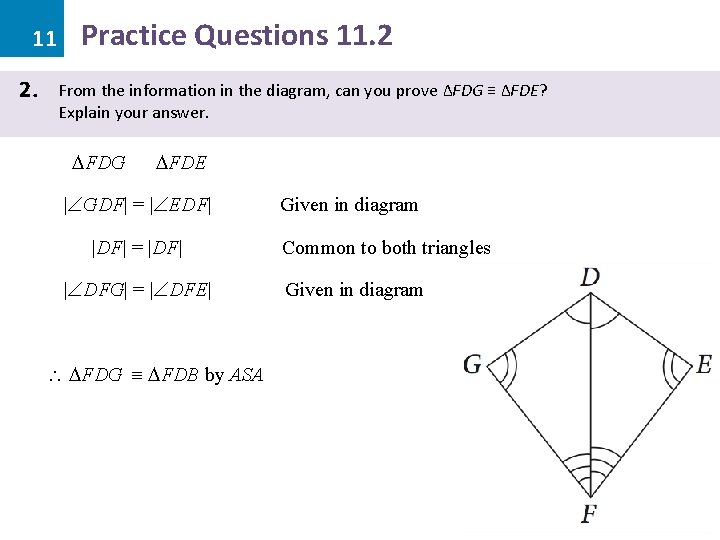
11 2. Practice Questions 11. 2 From the information in the diagram, can you prove ΔFDG ≡ ΔFDE? Explain your answer. FDG FDE | GDF| = | EDF| |DF| = |DF| | DFG| = | DFE| FDG FDB by ASA Given in diagram Common to both triangles Given in diagram

11 3. Practice Questions 11. 2 State whether ΔABC and ΔAED are congruent. Justify

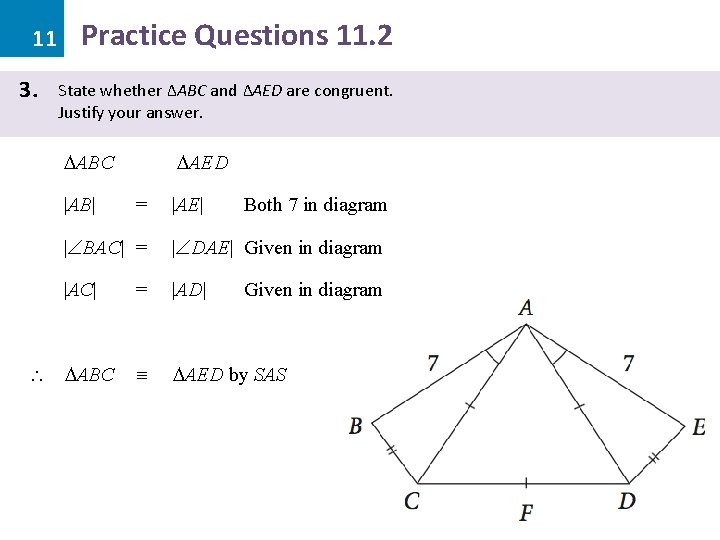
11 3. Practice Questions 11. 2 State whether ΔABC and ΔAED are congruent. Justify your answer. ABC |AB| AED = |AE| Both 7 in diagram | BAC| = | DAE| Given in diagram |AC| = |AD| AED by SAS ABC Given in diagram

11 4. Practice Questions 11. 2 Is there enough information to prove the two

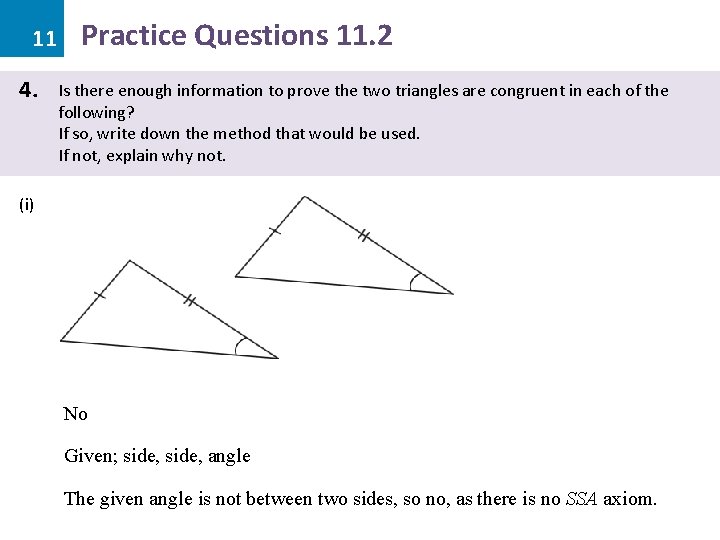
11 4. Practice Questions 11. 2 Is there enough information to prove the two triangles are congruent in each of the following? If so, write down the method that would be used. If not, explain why not. (i) No Given; side, angle The given angle is not between two sides, so no, as there is no SSA axiom.

11 4. Practice Questions 11. 2 Is there enough information to prove the two

11 4. Practice Questions 11. 2 Is there enough information to prove the two triangles are congruent in each of the following? If so, write down the method that would be used. If not, explain why not. (ii) Yes ; SAS

11 4. Practice Questions 11. 2 Is there enough information to prove the two

11 4. Practice Questions 11. 2 Is there enough information to prove the two triangles are congruent in each of the following? If so, write down the method that would be used. If not, explain why not. (iii) Yes ; RHS

11 4. Practice Questions 11. 2 Is there enough information to prove the two

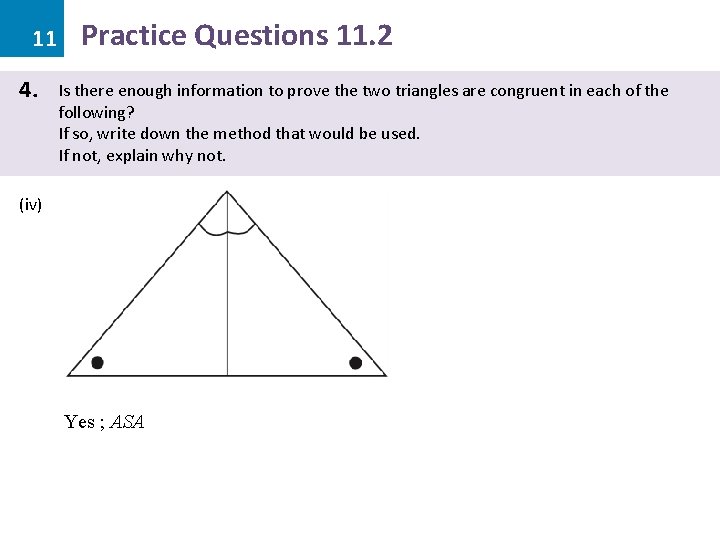
11 4. Practice Questions 11. 2 Is there enough information to prove the two triangles are congruent in each of the following? If so, write down the method that would be used. If not, explain why not. (iv) Yes ; ASA

11 4. Practice Questions 11. 2 Is there enough information to prove the two

11 4. Practice Questions 11. 2 Is there enough information to prove the two triangles are congruent in each of the following? If so, write down the method that would be used. If not, explain why not. (v) Yes ; SSS

11 4. Practice Questions 11. 2 Is there enough information to prove the two

11 4. Practice Questions 11. 2 Is there enough information to prove the two triangles are congruent in each of the following? If so, write down the method that would be used. If not, explain why not. (vi) No Given ; Angle, Angle No AAA axiom

11 4. Practice Questions 11. 2 Is there enough information to prove the two

11 4. Practice Questions 11. 2 Is there enough information to prove the two triangles are congruent in each of the following? If so, write down the method that would be used. If not, explain why not. (vii) Yes ; RHS

11 4. Practice Questions 11. 2 Is there enough information to prove the two

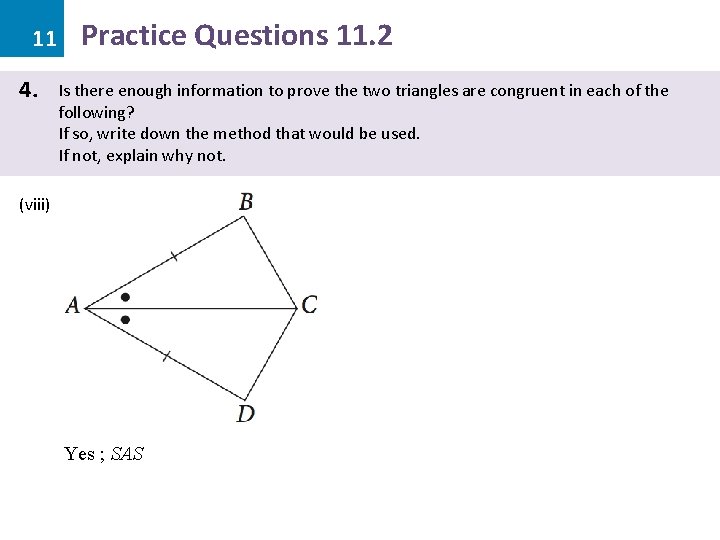
11 4. Practice Questions 11. 2 Is there enough information to prove the two triangles are congruent in each of the following? If so, write down the method that would be used. If not, explain why not. (viii) Yes ; SAS

11 5. Practice Questions 11. 2 An architect is designing a window in a

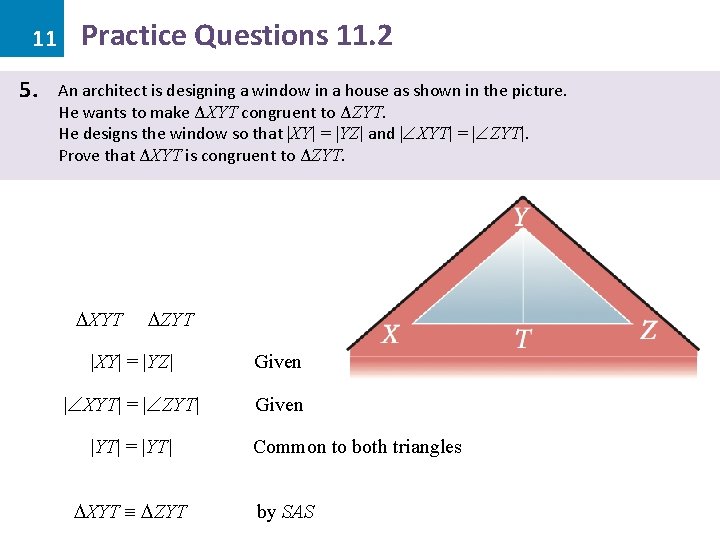
11 5. Practice Questions 11. 2 An architect is designing a window in a house as shown in the picture. He wants to make ΔXYT congruent to ΔZYT. He designs the window so that |XY| = |YZ| and | XYT| = | ZYT|. Prove that ΔXYT is congruent to ΔZYT. XYT ZYT |XY| = |YZ| Given | XYT| = | ZYT| Given |YT| = |YT| XYT ZYT Common to both triangles by SAS