Geometry Construction 1 Construct a segment congruent to

Geometry

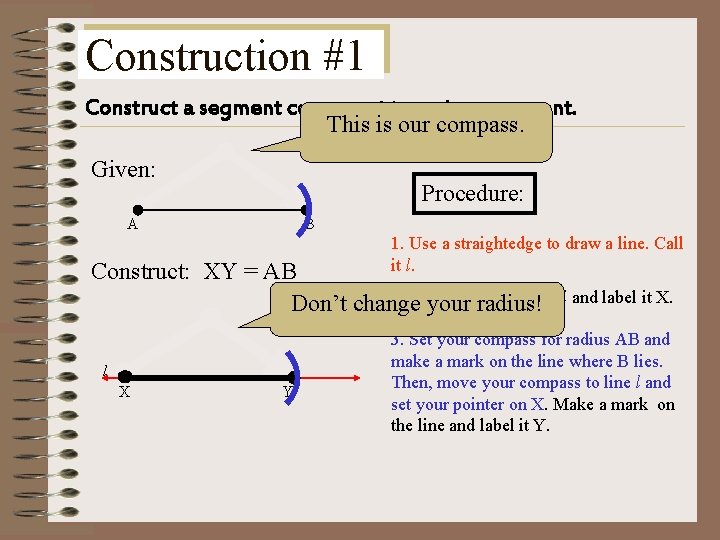
Construction #1 Construct a segment congruent to a given segment. This is our compass. Given: Procedure: A B 1. Use a straightedge to draw a line. Call it l. Construct: XY = AB 2. Choose point on l and label it X. Don’t change yourany radius! l X Y 3. Set your compass for radius AB and make a mark on the line where B lies. Then, move your compass to line l and set your pointer on X. Make a mark on the line and label it Y.

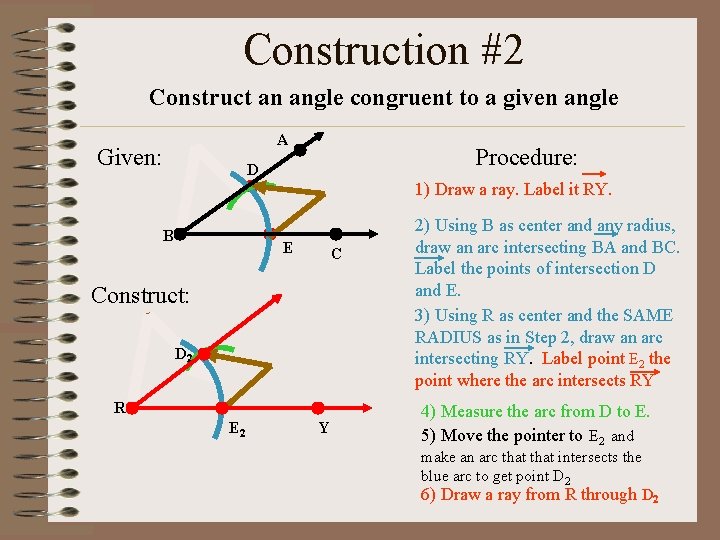
Construction #2 Construct an angle congruent to a given angle A Given: Procedure: D 1) Draw a ray. Label it RY. B E C Construct: D 2 R E 2 Y 2) Using B as center and any radius, draw an arc intersecting BA and BC. Label the points of intersection D and E. 3) Using R as center and the SAME RADIUS as in Step 2, draw an arc intersecting RY. Label point E 2 the point where the arc intersects RY 4) Measure the arc from D to E. 5) Move the pointer to E 2 and make an arc that intersects the blue arc to get point D 2 6) Draw a ray from R through D 2

Construction #3 How do I construct a Bisector of a given angle? A Given: Z X B Procedure: 1. 2. Y C Using B as center and any radius, draw and arc that intersects BA at X and BC at point Y. 2. Using X as center and a suitable radius, draw and arc. Using Y as center and the same radius, draw an arc that intersects the arc with center X at point Z. 3. Draw BZ.

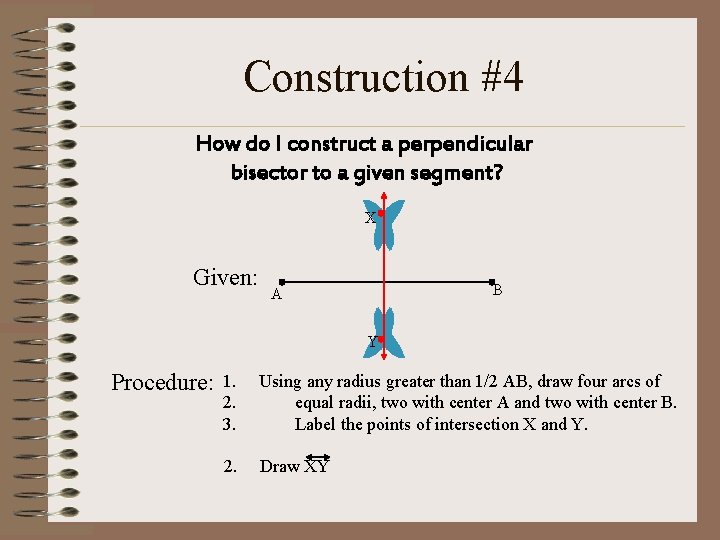
Construction #4 How do I construct a perpendicular bisector to a given segment? X Given: B A Y Procedure: 1. 2. 3. Using any radius greater than 1/2 AB, draw four arcs of equal radii, two with center A and two with center B. Label the points of intersection X and Y. 2. Draw XY

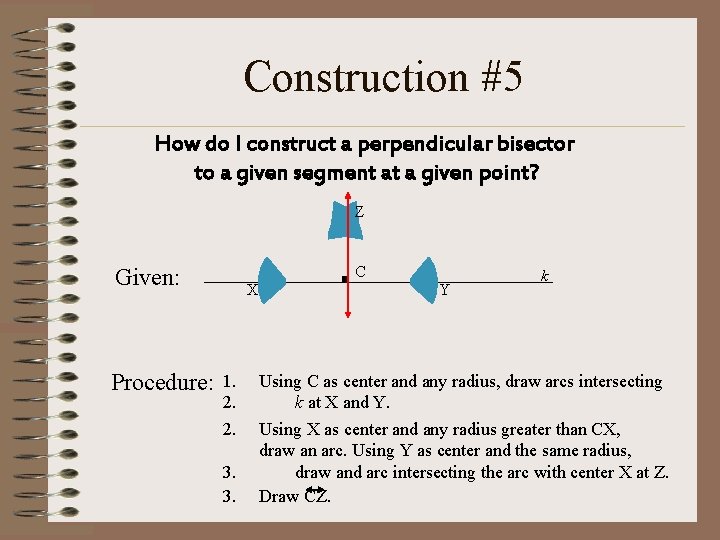
Construction #5 How do I construct a perpendicular bisector to a given segment at a given point? Z C Given: Procedure: X 1. 2. 2. 3. 3. Y k Using C as center and any radius, draw arcs intersecting k at X and Y. Using X as center and any radius greater than CX, draw an arc. Using Y as center and the same radius, draw and arc intersecting the arc with center X at Z. Draw CZ.

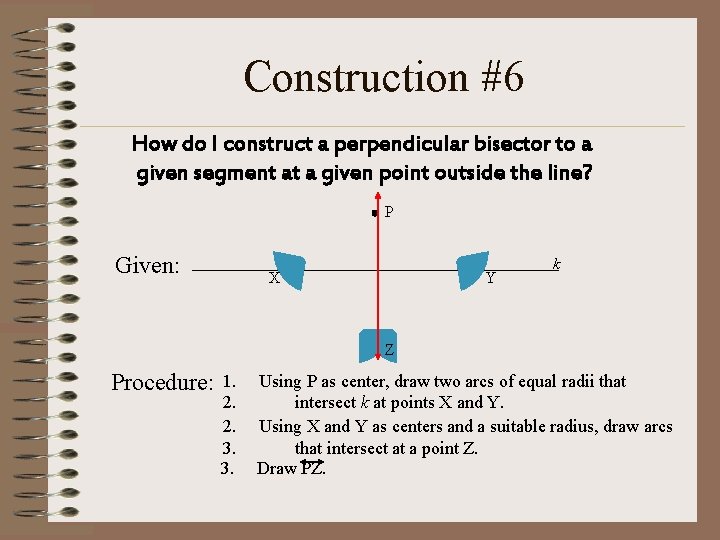
Construction #6 How do I construct a perpendicular bisector to a given segment at a given point outside the line? P Given: X Y k Z Procedure: 1. 2. 2. 3. 3. Using P as center, draw two arcs of equal radii that intersect k at points X and Y. Using X and Y as centers and a suitable radius, draw arcs that intersect at a point Z. Draw PZ.

Construction #7 How do I construct a line parallel to a given line through a given point? P 1 Given: Procedure: A l B k 1. Let A and B be two points on line k. Draw PA. 2. 3. 4. At P, construct <1 so that <1 and <PAB are congruent corresponding angles. Let l be the line containing the ray you just constructed.

Concurrent Lines If the lines are Concurrent then they all intersect at the same point. The point of intersection is called the “point of concurrency”

What are the 4 different types of concurrent lines for a triangle? Concurrent Lines Point of Concurrency I. Perpendicular bisectors ØCircumcenter II. Angle bisectors ØIncenter III. Altitudes ØOrthocenter IV. Medians ØCentriod Circumcenter Incenter SP Orthocenter SP SP Centroid SP

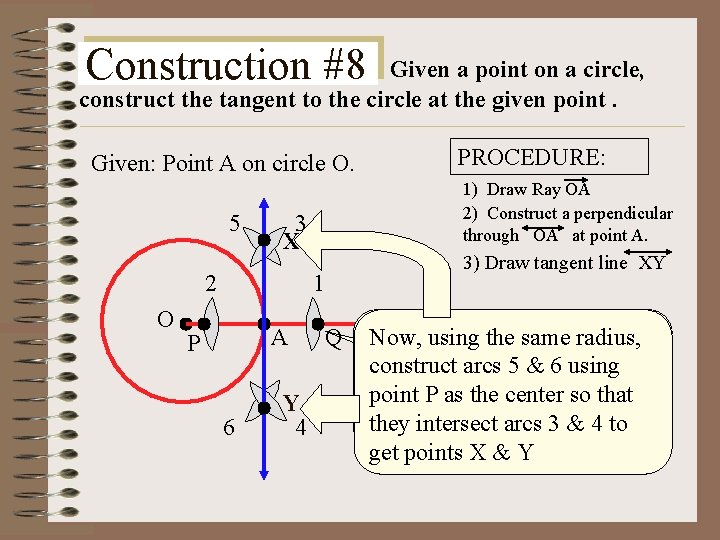
Construction #8 Given a point on a circle, construct the tangent to the circle at the given point. Given: Point A on circle O. 5 O 1) Draw Ray OA 2) Construct a perpendicular through OA at point A. 3 X 2 3) Draw tangent line XY 1 A P 6 Y 4 PROCEDURE: Q Construct arcs & 4 using Now, using the 3 same radius, point Q asarcs the center and any construct 5 & 6 using Construct 1 and 2 that suitable radius (keep this point P as thearcs center so using any suitable radius) they intersect arcs 3 & 4 to A as. Xthe getand points & center Y

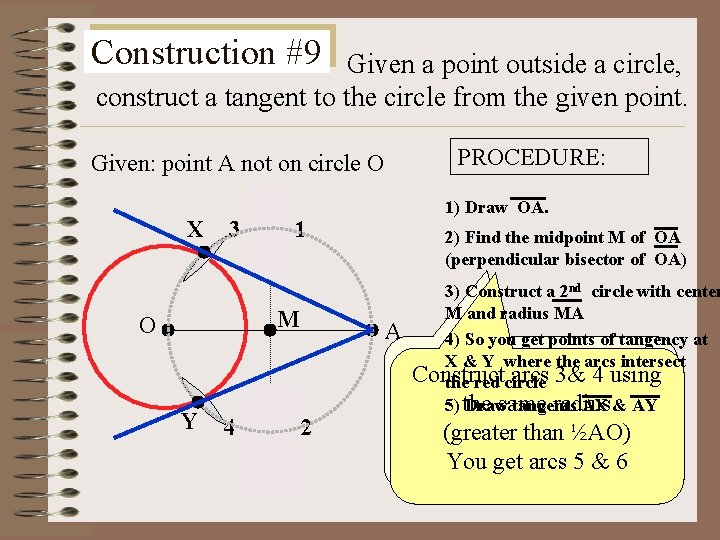
Construction #9 Given a point outside a circle, construct a tangent to the circle from the given point. Given: point A not on circle O X 3 1 M O Y 4 2 PROCEDURE: 1) Draw OA. 2) Find the midpoint M of OA (perpendicular bisector of OA) 3) Construct a 2 nd circle with center M and radius MA A 4) So you get points of tangency at X & Y where the arcs intersect Construct arcs 1& 2 using Construct arcs 3& 4 using the red circle a suitable radius greater 5) the Draw tangents AX & AY same radius than ½AO½AO) (greater ( keep Youthis getradius arcs 5 for & 6 the next step)

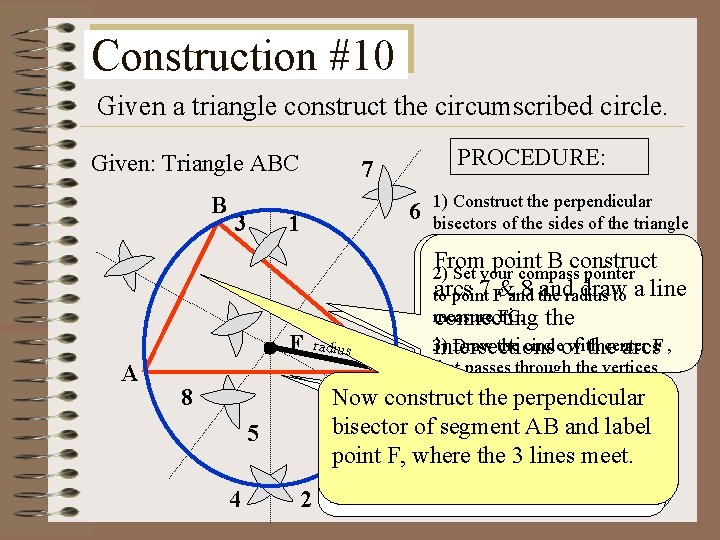
Construction #10 Given a triangle construct the circumscribed circle. Given: Triangle ABC B 3 6 1 F A radius 8 5 4 PROCEDURE: 7 2 1) Construct the perpendicular bisectors of the sides of the triangle and label the point of intersection F. Bisect From point segment B construct BC; Using 2) Set your compass pointer ato arcs radius 7 F&and greater 8 the andradius draw thanto a line point measure FC. the 1/2 BC connecting from point C 3) Draw the arcs circleof construct intersections 5 with & thecenter 6 arcs. F , C that passes through the vertices A, B, & C Now construct the perpendicular bisector of segment and a 3 label Bisectpoint segment AC; AB Using From A construct arcs & where theconnecting 31/2 AC lines meet. radius greater than from 4 point and F, draw a line the point C construct intersections of thearcs 1 & 2

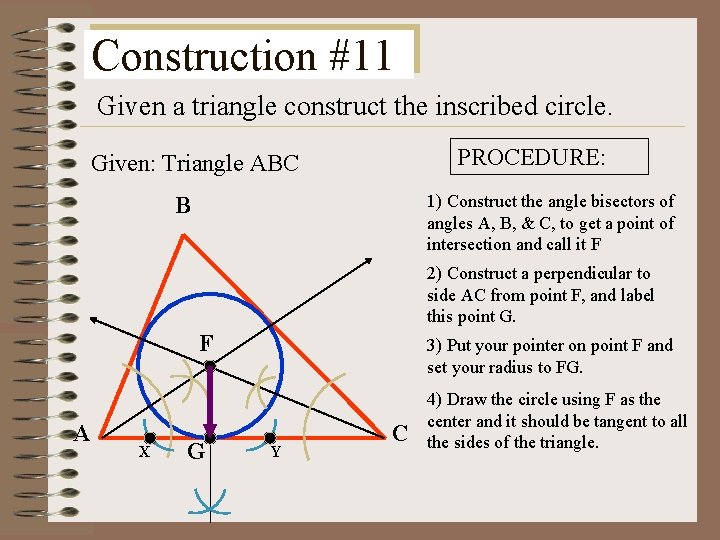
Construction #11 Given a triangle construct the inscribed circle. PROCEDURE: Given: Triangle ABC 1) Construct the angle bisectors of angles A, B, & C, to get a point of intersection and call it F B 2) Construct a perpendicular to side AC from point F, and label this point G. F A X G 3) Put your pointer on point F and set your radius to FG. Y C 4) Draw the circle using F as the center and it should be tangent to all the sides of the triangle.

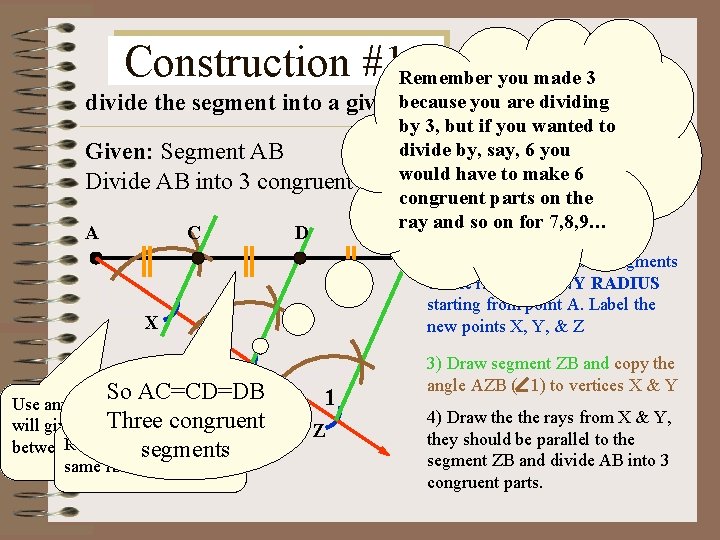
Construction #12 Given a segment, Remember you made 3 youofare dividing parts. divide the segment into a givenbecause number congruent Given: Segment AB Divide AB into 3 congruent A C D by 3, but if you wanted to divide by, say, 6 you PROCEDURE: would have to make 6 parts. congruent parts on RAY the from 1) Construct ANY raypoint and A sothat’s on for not 7, 8, 9… AB B 2) Construct 3 congruent segments on the ray using ANY RADIUS starting from point A. Label the new points X, Y, & Z X Y So AC=CD=DB Use any suitable radius that Three congruent will give some distance keep the between. Remember the pointssegments same radius!! 1 Z 3) Draw segment ZB and copy the angle AZB ( 1) to vertices X & Y 4) Draw the rays from X & Y, they should be parallel to the segment ZB and divide AB into 3 congruent parts.

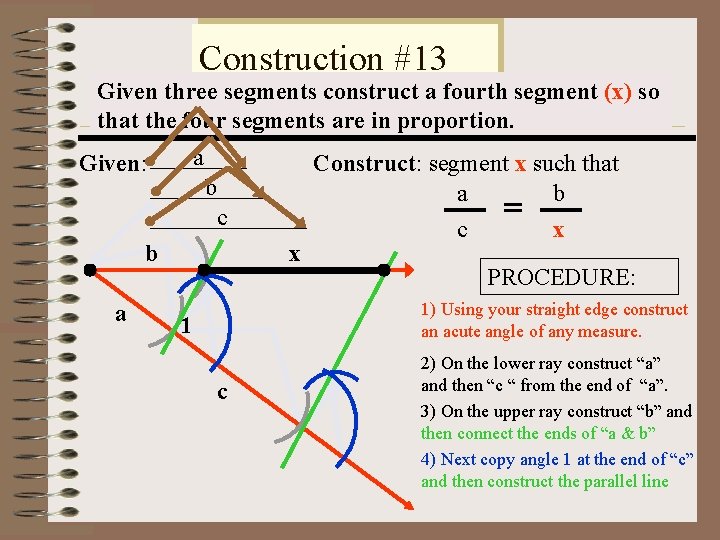
Construction #13 Given three segments construct a fourth segment (x) so that the four segments are in proportion. a Given: b c x b a Construct: segment x such that a b c x PROCEDURE: 1) Using your straight edge construct an acute angle of any measure. 1 c 2) On the lower ray construct “a” and then “c “ from the end of “a”. 3) On the upper ray construct “b” and then connect the ends of “a & b” 4) Next copy angle 1 at the end of “c” and then construct the parallel line

Construction #14 Given 2 segments construct their geometric mean. Mark off 2 arcs from Y. a Keep the same radius and that: Given: Construct: segment x such sure radius b Make mark offto 2 set more arcs from a your x to. X, more thancrossing 1/2 NM then: xfirst two. b Mark 2 arcs from M. on Keep the same Mark off 2 equal distances either radius and. Omark 2 more arcs orange segment is xoff the PROCEDURE: of point using any radius andfrom N, 9 7 3 The 1 side Q K then crossing the first two. geometric mean between the bisect this new segment 1) Draw a ray and mark off a+b. the bperpendicular bisector PQpoint M. lengths. Draw of a and 2) Bisect a+b (XY) and label 6 5 through point O from O to M, X Y 3) Construct M (I used the distance the circle with center M N a O but b remember any and radius = will MY do) (or MX) X 8 10 2 4 P L 4) Construct a perpendicular where segment “a” meets segment “b” (point O)

The Meaning of Locus If a figure is a locus then it is the set of all points that satisfy one or more conditions. The term “locus” is just a technical term meaning “a set of points”. So , a circle is a locus. Why? ? Because it is a set of points a given distance from a given point.

What can a locus be? ? Remember it is a SET OF POINTS so if you recall the idea of sets from algebra it is possible for a set to be empty. So a set could be: A. The empty set. (no points fit the condition or conditions) B. A single point. C. Two points, three points…. D. An infinite set of points. (like a line, circle, curve, …)

Examples of a Locus in a Plane

Locus Problems