Geometry Chord Lengths Section 6 3 Geometry Mrs

Geometry Today’s Standards • MM 2 G 3. Students will understand the properties of

Geometry Using Chords of Circles • A point Y is called the midpoint of

Geometry Theorem 6. 5 – covered already • In the same circle, or in

Ex. 4: Using Theorem 6. 5 Geometry D • You can use Theorem 6.

Geometry Theorem 6. 6 • If one chord is a perpendicular bisector of another

Geometry Ex. 5: Finding the Center of a Circle • Theorem 6. 6 can

Geometry Ex. 5: Finding the Center of a Circle • Step 2: Draw the

Geometry Ex. 5: Finding the Center of a Circle • Step 3: The perpendicular

Geometry Theorem 6. 7 • If a diameter of a circle is perpendicular to

Geometry Theorem 6. 7 Proof If diameter is to a Chord Then BE DE

Geometry Theorem 6. 8 • In the same circle, or in congruent circles, two

Geometry Theorem 6. 8 Proof (forwards): If 2 chords are Then AB = AC

Geometry Theorem 6. 8 Proof (reverse): If AB = AC Then 2 chords are

Geometry Practice • 11 -3 Study Guide • 11 -4 Practice – skip problems

Geometry Ex. 7: Using Theorem 6. 8 AB = 8; DE = 8, and

Slides: 16

Download presentation

Geometry Chord Lengths Section 6. 3 Geometry Mrs. Spitz Spring 2005 Modified By Mr. Moss, Spring 2011

Geometry Today’s Standards • MM 2 G 3. Students will understand the properties of circles. • a. Understand use properties of chords, tangents, and secants as an application of triangle similarity. • d. Justify measurements and relationships in circles using geometric and algebraic properties.

Geometry Using Chords of Circles • A point Y is called the midpoint of if . Any line, segment, or ray that contains Y bisects.

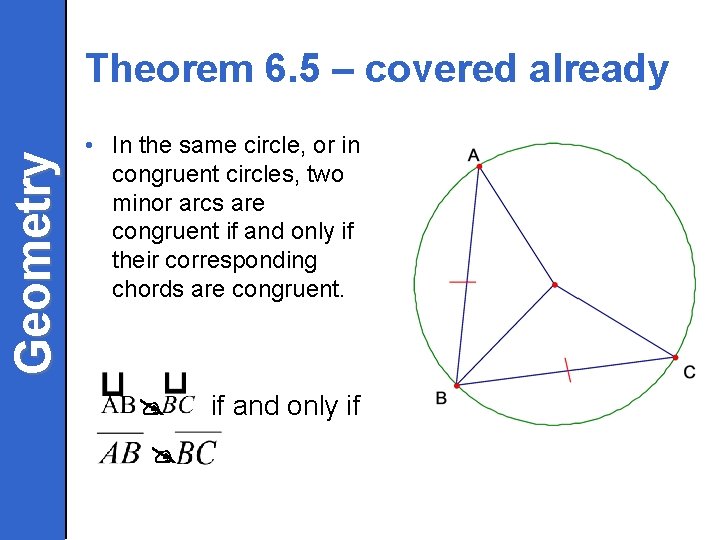
Geometry Theorem 6. 5 – covered already • In the same circle, or in congruent circles, two minor arcs are congruent if and only if their corresponding chords are congruent. if and only if

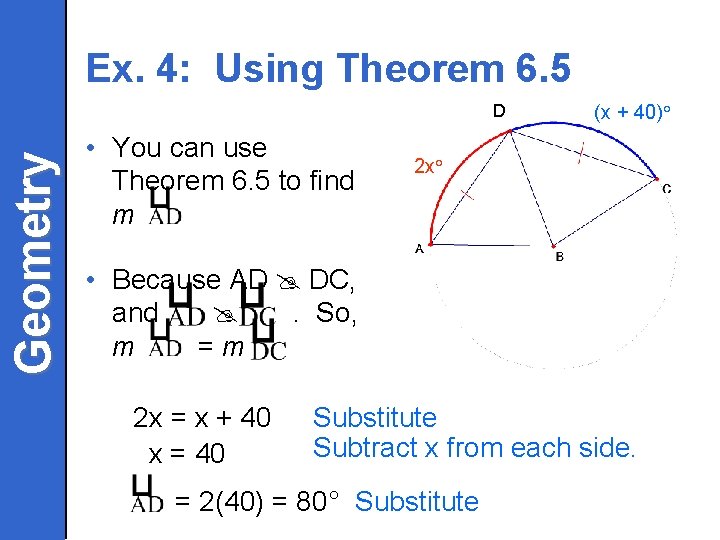
Ex. 4: Using Theorem 6. 5 Geometry D • You can use Theorem 6. 5 to find m (x + 40)° 2 x° • Because AD DC, and . So, m =m 2 x = x + 40 x = 40 Substitute Subtract x from each side. = 2(40) = 80° Substitute

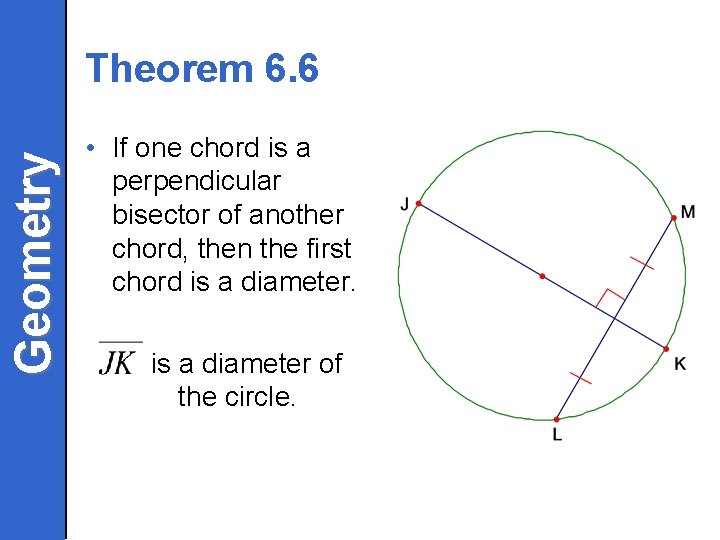
Geometry Theorem 6. 6 • If one chord is a perpendicular bisector of another chord, then the first chord is a diameter of the circle.

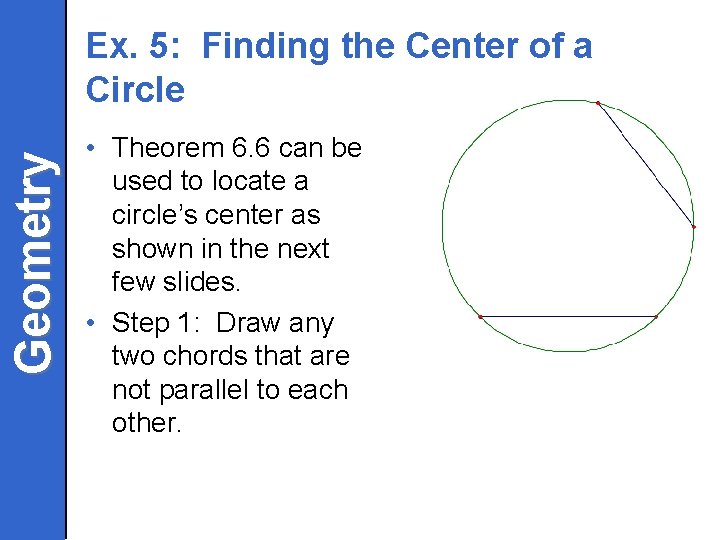
Geometry Ex. 5: Finding the Center of a Circle • Theorem 6. 6 can be used to locate a circle’s center as shown in the next few slides. • Step 1: Draw any two chords that are not parallel to each other.

Geometry Ex. 5: Finding the Center of a Circle • Step 2: Draw the perpendicular bisector of each chord. These are the diameters.

Geometry Ex. 5: Finding the Center of a Circle • Step 3: The perpendicular bisectors intersect at the circle’s center.

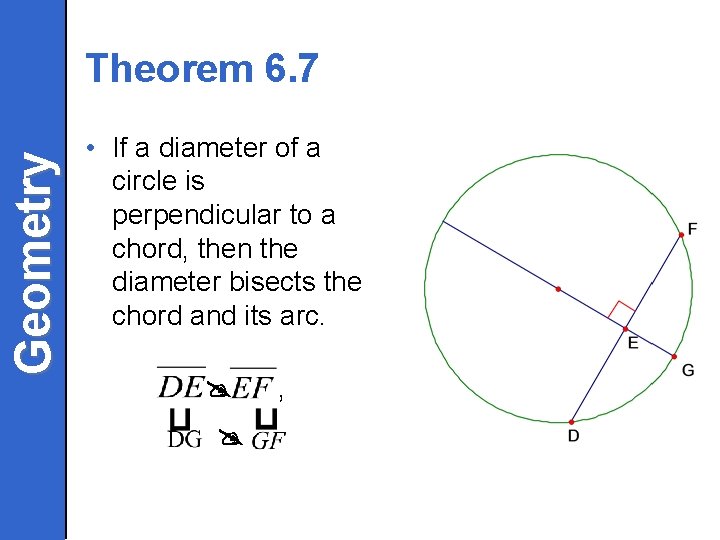
Geometry Theorem 6. 7 • If a diameter of a circle is perpendicular to a chord, then the diameter bisects the chord and its arc. ,

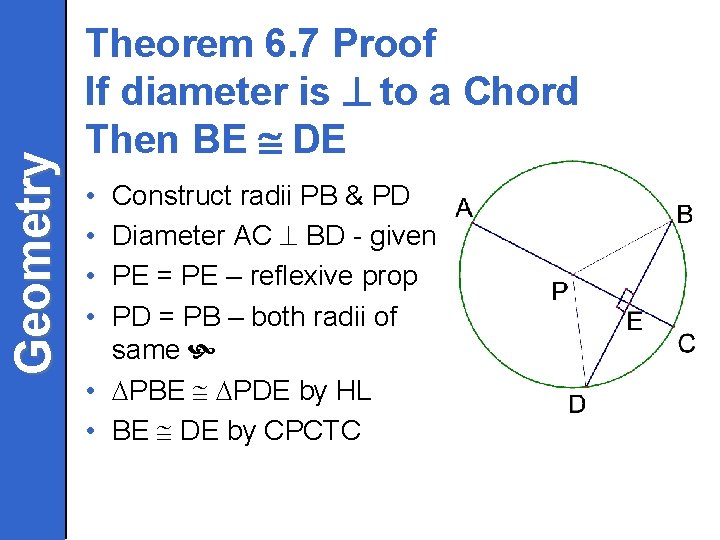
Geometry Theorem 6. 7 Proof If diameter is to a Chord Then BE DE • • Construct radii PB & PD Diameter AC BD - given PE = PE – reflexive prop PD = PB – both radii of same • PBE PDE by HL • BE DE by CPCTC

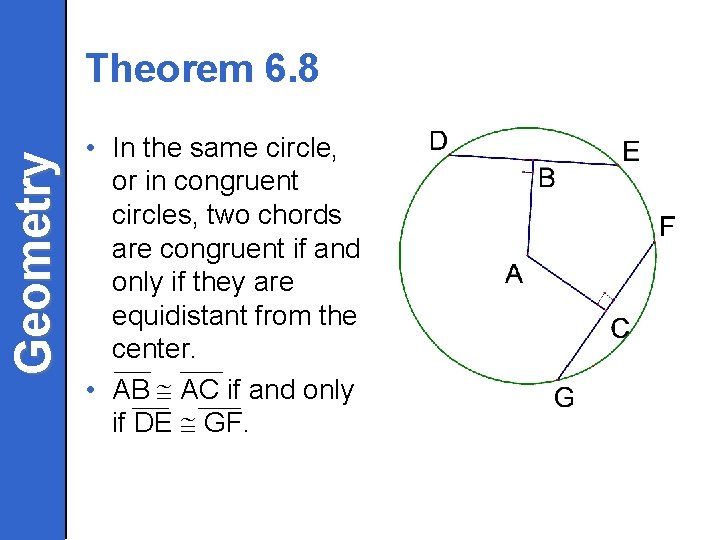
Geometry Theorem 6. 8 • In the same circle, or in congruent circles, two chords are congruent if and only if they are equidistant from the center. • AB AC if and only if DE GF.

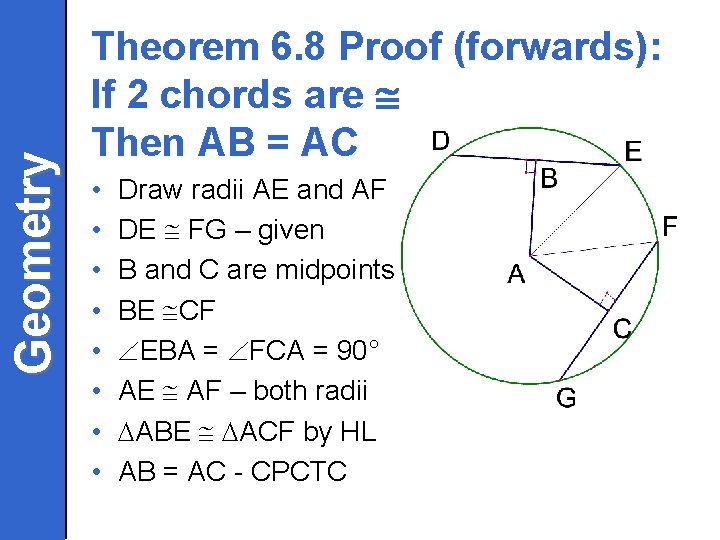
Geometry Theorem 6. 8 Proof (forwards): If 2 chords are Then AB = AC • • Draw radii AE and AF DE FG – given B and C are midpoints BE CF EBA = FCA = 90° AE AF – both radii ABE ACF by HL AB = AC - CPCTC

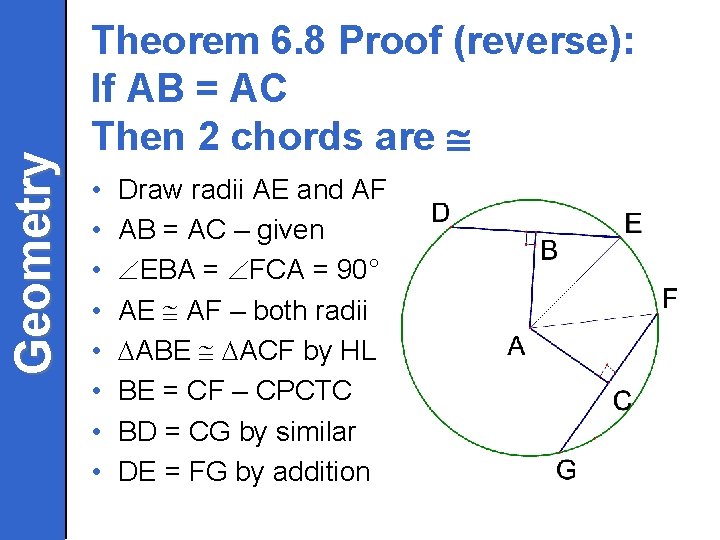
Geometry Theorem 6. 8 Proof (reverse): If AB = AC Then 2 chords are • • Draw radii AE and AF AB = AC – given EBA = FCA = 90° AE AF – both radii ABE ACF by HL BE = CF – CPCTC BD = CG by similar DE = FG by addition

Geometry Practice • 11 -3 Study Guide • 11 -4 Practice – skip problems 1 & 2 • HW: Pg 201, # 1 – 13 all

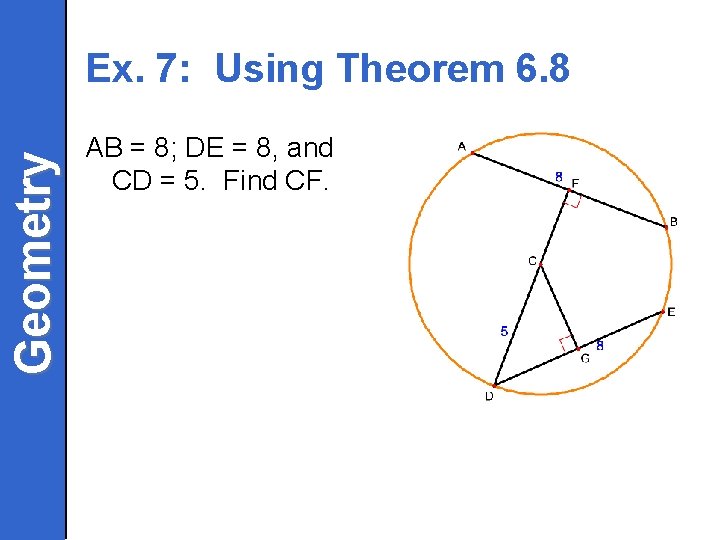
Geometry Ex. 7: Using Theorem 6. 8 AB = 8; DE = 8, and CD = 5. Find CF.