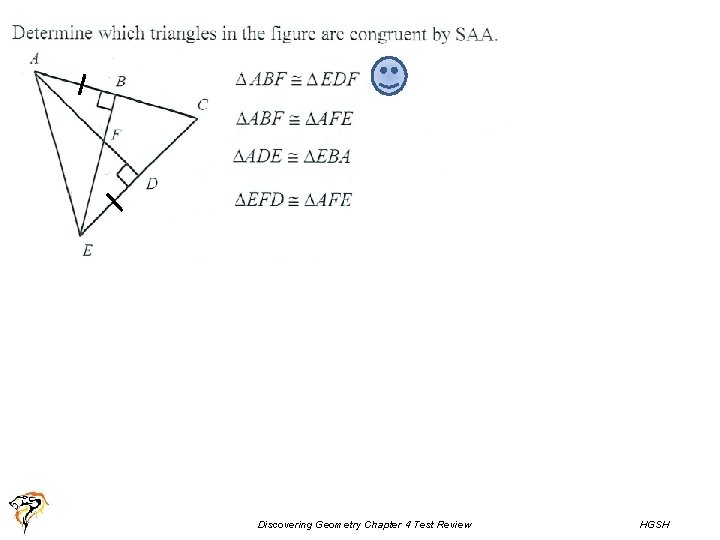
GEOMETRY CHAPTER 4 TEST REVIEW Discovering Geometry Chapter

A A 1 2 4 S 3 1 and 2 are Vertical Angles. 3

BC = (8 X +3) YZ = (7 X +5) Because of the way

Triangle Sum Conjecture B = 180° – (60° + 45°) B = 75° 45°

50° 65° By the Triangle Exterior Angle Conjecture x= 50° + 65° x= 115°

By the Triangle Inequality Conjecture, the sum of two of the legs has to

55° 45° 110° B C 88° 180° By the Triangle Exterior Angle Conjecture x

AD CD ADB CDB and BD is common to both triangles. Therefore we have

4 cm, 15 cm, 20 cm 12 cm, 11 cm, 20 cm 5 cm,

Discovering Geometry Chapter 4 Test Review HGSH

100° By the Isosceles Triangle Conjecture, the base angles of this Isosceles triangle are

20 ft. By the Converse of the Isosceles Triangle Conjecture The Triangle is an

Segment BD, the Angle Bisector of Isosceles Triangle ABC, is also the perpendicular bisector

By the Converse of the Isosceles Triangle Conjecture, the Triangle is an Isosceles, but

Slides: 19

Download presentation

GEOMETRY CHAPTER 4 TEST REVIEW Discovering Geometry Chapter 4 Test Review HGSH

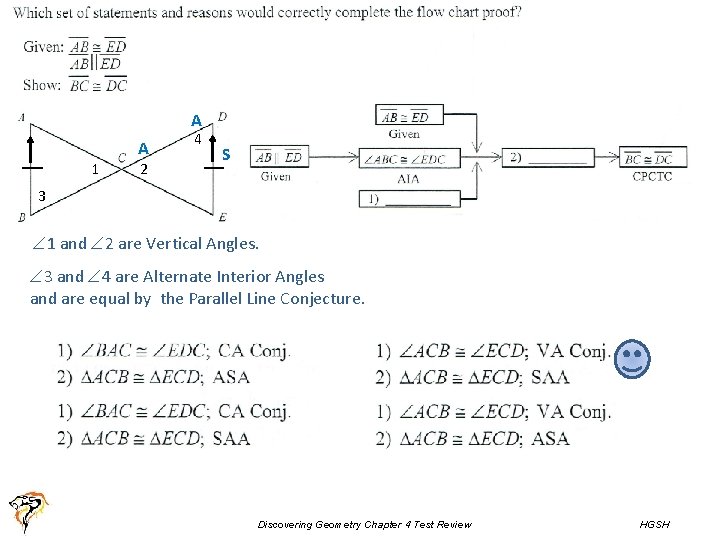
A A 1 2 4 S 3 1 and 2 are Vertical Angles. 3 and 4 are Alternate Interior Angles and are equal by the Parallel Line Conjecture. Discovering Geometry Chapter 4 Test Review HGSH

BC = (8 X +3) YZ = (7 X +5) Because of the way the triangle congruence is written A and X are corresponding angles C and Z are corresponding angles BC and YZ are corresponding, So: BC = YZ 8 x + 3 = 7 x + 5 , subtract 7 x x+3 = 5 x=2 , subtract 3 Discovering Geometry Chapter 4 Test Review HGSH

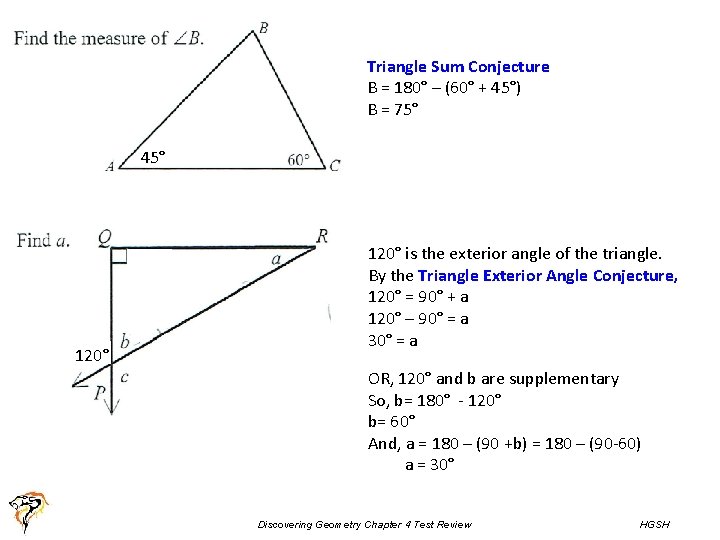
Triangle Sum Conjecture B = 180° – (60° + 45°) B = 75° 45° 120° is the exterior angle of the triangle. By the Triangle Exterior Angle Conjecture, 120° = 90° + a 120° – 90° = a 30° = a OR, 120° and b are supplementary So, b= 180° - 120° b= 60° And, a = 180 – (90 +b) = 180 – (90 -60) a = 30° Discovering Geometry Chapter 4 Test Review HGSH

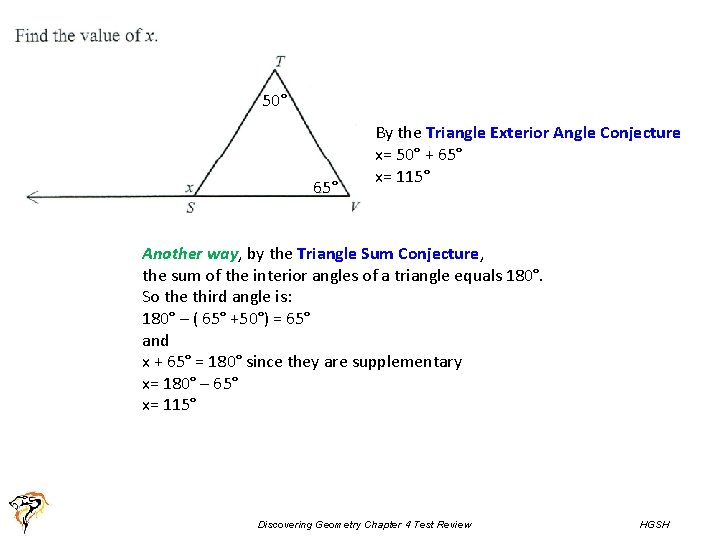
50° 65° By the Triangle Exterior Angle Conjecture x= 50° + 65° x= 115° Another way, by the Triangle Sum Conjecture, the sum of the interior angles of a triangle equals 180°. So the third angle is: 180° – ( 65° +50°) = 65° and x + 65° = 180° since they are supplementary x= 180° – 65° x= 115° Discovering Geometry Chapter 4 Test Review HGSH

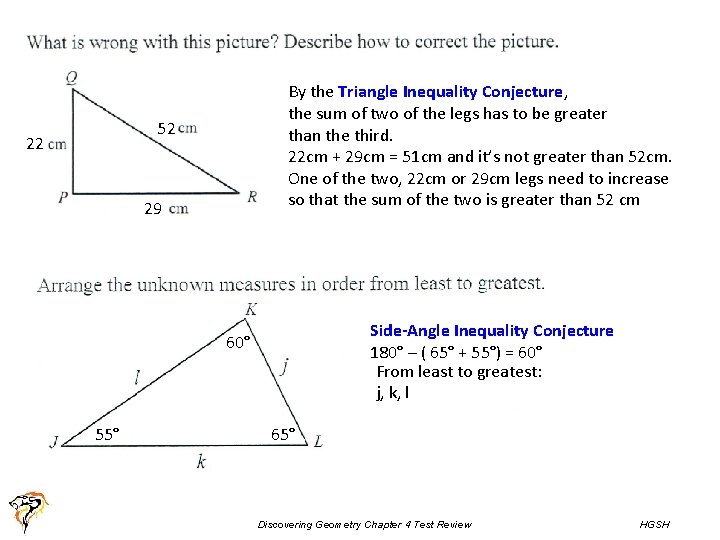
By the Triangle Inequality Conjecture, the sum of two of the legs has to be greater than the third. 22 cm + 29 cm = 51 cm and it’s not greater than 52 cm. One of the two, 22 cm or 29 cm legs need to increase so that the sum of the two is greater than 52 cm 52 22 29 Side-Angle Inequality Conjecture 180° – ( 65° + 55°) = 60° From least to greatest: j, k, l 60° 55° 65° Discovering Geometry Chapter 4 Test Review HGSH

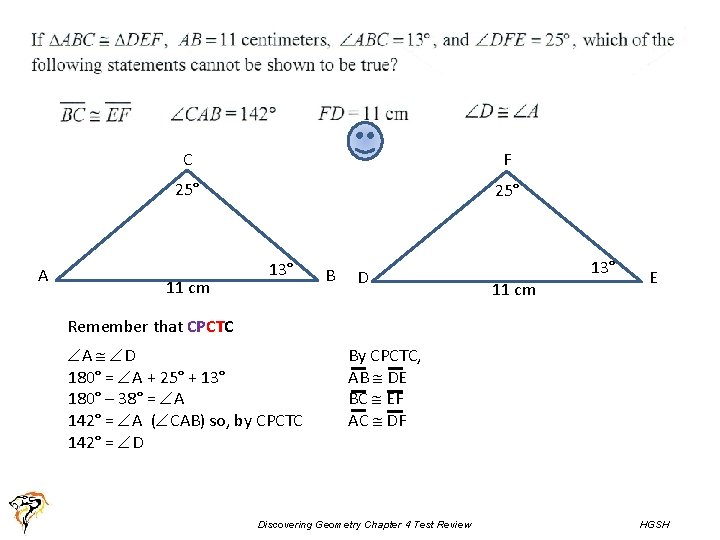
C F 25° z A 11 cm 13° B D 13° 11 cm E Remember that CPCTC A D 180° = A + 25° + 13° 180° – 38° = A 142° = A ( CAB) so, by CPCTC 142° = D By CPCTC, AB DE BC EF AC DF Discovering Geometry Chapter 4 Test Review HGSH

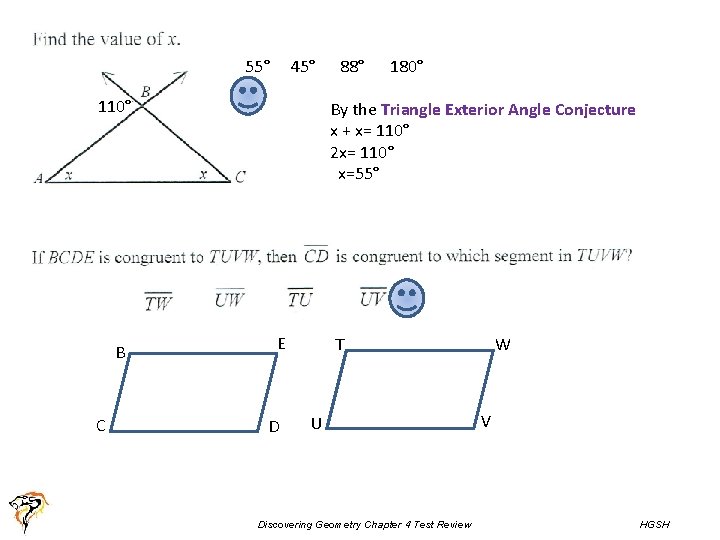
55° 45° 110° B C 88° 180° By the Triangle Exterior Angle Conjecture x + x= 110° 2 x= 110° x=55° E D W T U Discovering Geometry Chapter 4 Test Review V HGSH

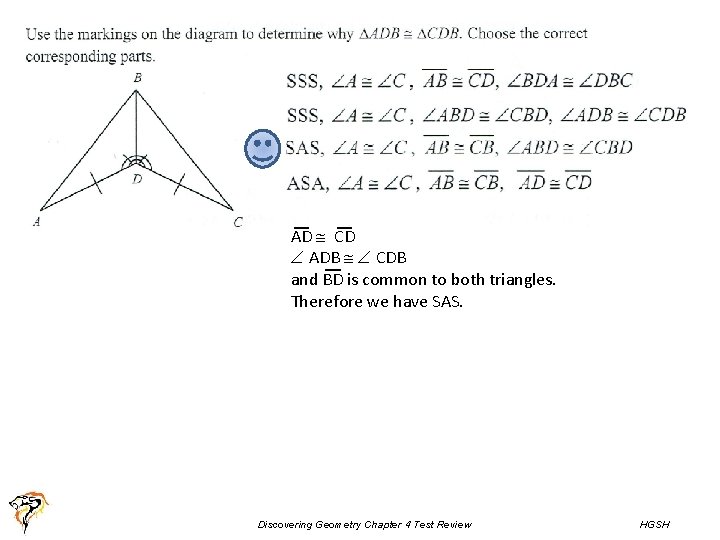
AD CD ADB CDB and BD is common to both triangles. Therefore we have SAS. Discovering Geometry Chapter 4 Test Review HGSH

4 cm, 15 cm, 20 cm 12 cm, 11 cm, 20 cm 5 cm, 10 cm 14 cm, 5 cm, 20 cm 101° x=79°; y=101° x=22°; y=101° x=79°; y=68° x=22°; y=79° Because the Triangle is an Isosceles Triangle, the base angles are equal. So, then y = 180° – 101° (Supplementary Angles) y=79° Therefore, 2 y+x= 180° 2(79°) + x = 180° – 158° = 22° Discovering Geometry Chapter 4 Test Review HGSH

Discovering Geometry Chapter 4 Test Review HGSH

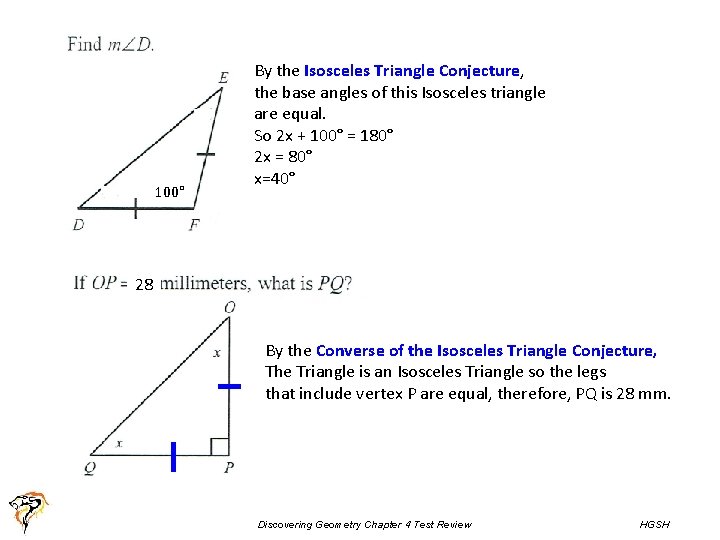
100° By the Isosceles Triangle Conjecture, the base angles of this Isosceles triangle are equal. So 2 x + 100° = 180° 2 x = 80° x=40° 28 By the Converse of the Isosceles Triangle Conjecture, The Triangle is an Isosceles Triangle so the legs that include vertex P are equal, therefore, PQ is 28 mm. Discovering Geometry Chapter 4 Test Review HGSH

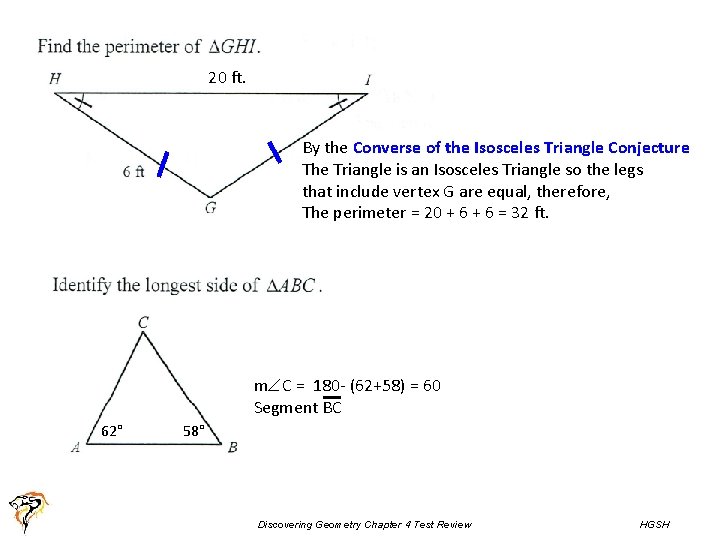
20 ft. By the Converse of the Isosceles Triangle Conjecture The Triangle is an Isosceles Triangle so the legs that include vertex G are equal, therefore, The perimeter = 20 + 6 = 32 ft. m C = 180 - (62+58) = 60 Segment BC 62° 58° Discovering Geometry Chapter 4 Test Review HGSH

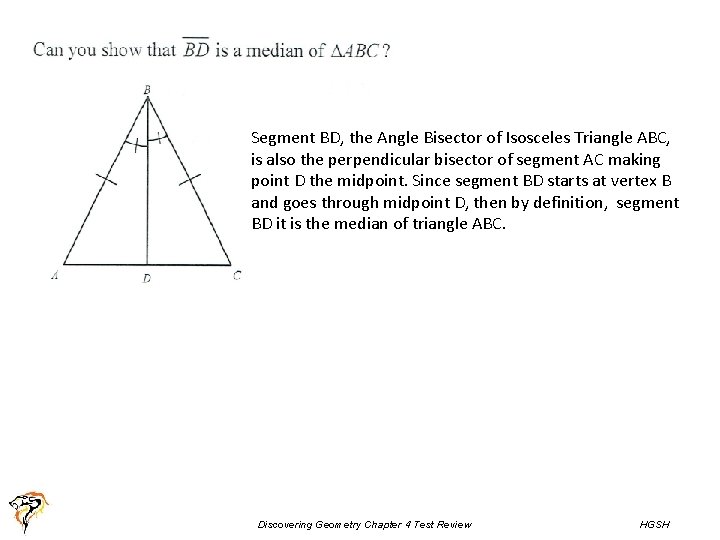
Segment BD, the Angle Bisector of Isosceles Triangle ABC, is also the perpendicular bisector of segment AC making point D the midpoint. Since segment BD starts at vertex B and goes through midpoint D, then by definition, segment BD it is the median of triangle ABC. Discovering Geometry Chapter 4 Test Review HGSH

By the Converse of the Isosceles Triangle Conjecture, the Triangle is an Isosceles, but since the base angles are 60°, then by the Triangle Sum Conjecture, 60 + x = 180, So x = 60, therefore making the triangle an equiangular, equilateral triangle. Therefore, 3 y = 33 yards. y = 11 yds. 16 in 15 in 17 in Discovering Geometry Chapter 4 Test Review HGSH

Discovering Geometry Chapter 4 Test Review HGSH