Geometry Chapter 2 2 2 ANALYZE CONDITIONAL STATEMENTS

Geometry Chapter 2 2 -2 ANALYZE CONDITIONAL STATEMENTS

Warm-Up • With a partner, come up with your own example of a statement that describes a pattern. It can be described in words, such as in example 1, or with a sequence of numbers. • I will select groups to share their statements with the class.

2 -2: Analyze Conditional Statements Objective: Students will be able to analyze and write conditional statements, identifying the hypothesis and conclusion. Agenda – Conditional Statements Definitions/Examples Converse Inverse Contrapositive Biconditional Statements

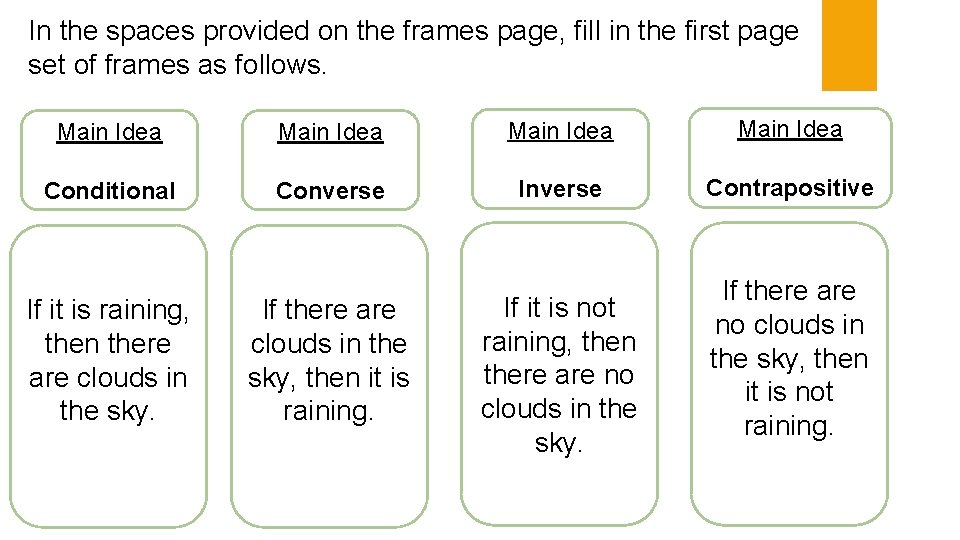
Logical Statements In the spaces provided on the Frame page, fill in the following Key Topic: Logical Statements Is about… Writing sentences using hypothesis and conclusions.

Conditional Statements A conditional statement is a logical statement that has two parts, a hypothesis and a conclusion. A conditional statement is typically written in “If-Then” form, where the “If” part contains the hypothesis, and the “Then” part contains the conclusion. Example: If it is raining, then there are clouds in the sky. Hypothesis Conclusion

Frames Page: Fill in the first main on idea with “Conditional Statement”, then fill in the essential details with the previous example. Main Idea Conditional If it is raining, then there are clouds in the sky. Main Idea

Related Statements Any conditional statement can be re-written in the following ways: The converse – Switches the hypothesis and conclusion of the conditional statement. The inverse – States the opposite (negation) of the hypothesis and conclusion. The contrapositive – States the opposite (negation) of the hypothesis and conclusion that the converse gives.

In the spaces provided on the frames page, fill in the first page set of frames as follows. Main Idea Conditional Converse Inverse Contrapositive If it is raining, then there are clouds in the sky. If there are clouds in the sky, then it is raining. If it is not raining, then there are no clouds in the sky. If there are no clouds in the sky, then it is not raining.

Verifying Statements Conditional statements, along with all of their alternate statements, can be true or false. To show that any of these statements are true, you must show that the conclusion is true every time the hypothesis is true. To show that any of them are false, you must provide a counterexample for each one.

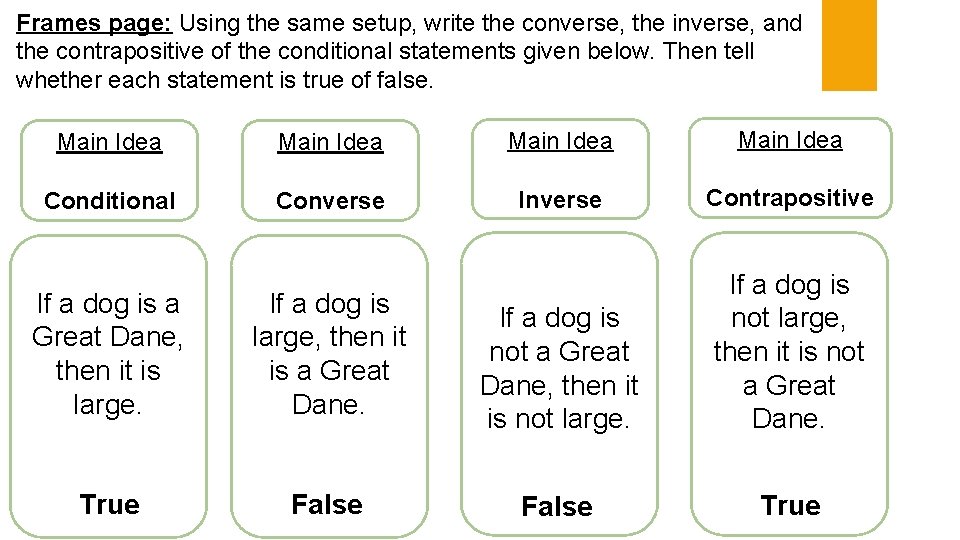
Frames page: Using the same setup, write the converse, the inverse, and the contrapositive of the conditional statements given below. Then tell whether each statement is true of false. Main Idea Conditional Converse Inverse Contrapositive If a dog is not a Great Dane, then it is not large. If a dog is not large, then it is not a Great Dane. False True If a dog is a Great Dane, then it is large. If a dog is large, then it is a Great Dane. True False

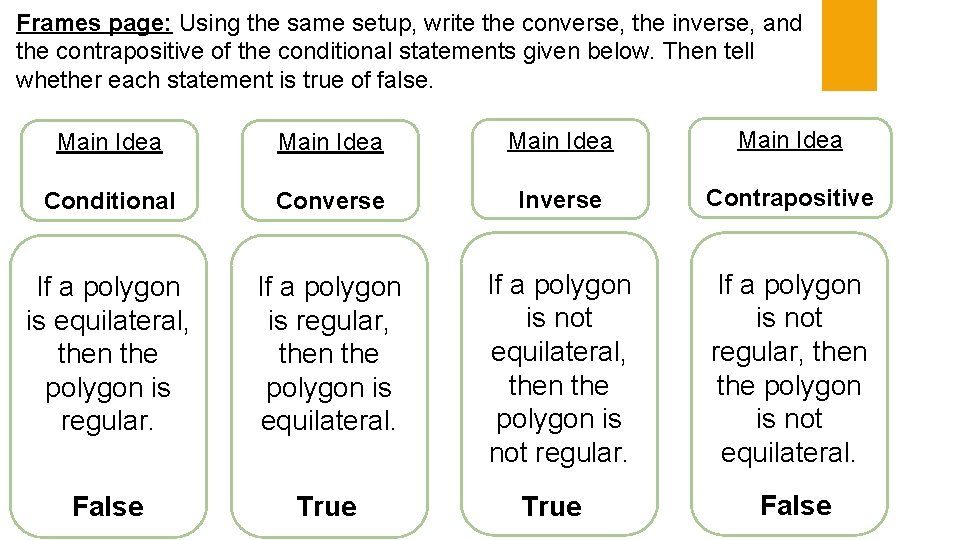
Frames page: Using the same setup, write the converse, the inverse, and the contrapositive of the conditional statements given below. Then tell whether each statement is true of false. Main Idea Conditional Converse Inverse Contrapositive If a polygon is equilateral, then the polygon is regular. If a polygon is regular, then the polygon is equilateral. If a polygon is not equilateral, then the polygon is not regular. If a polygon is not regular, then the polygon is not equilateral. False True False

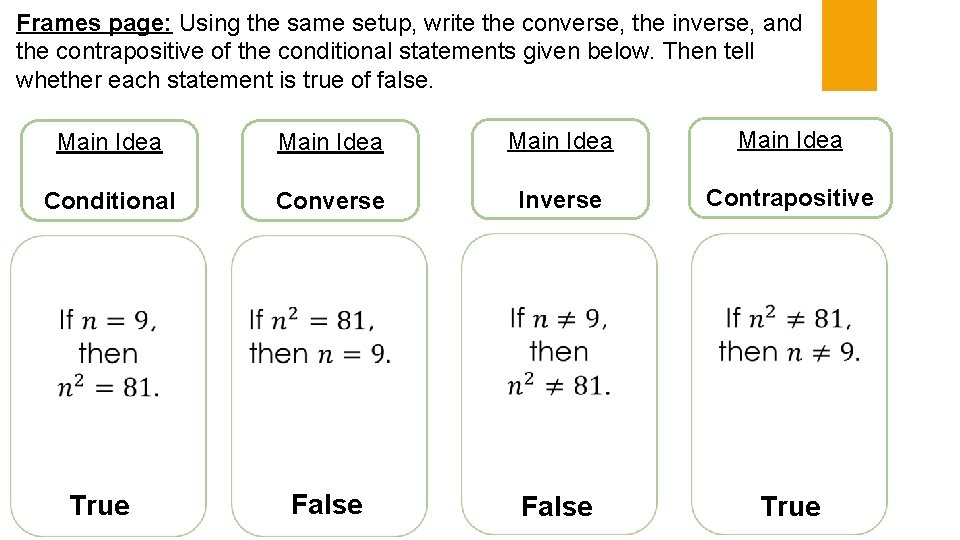
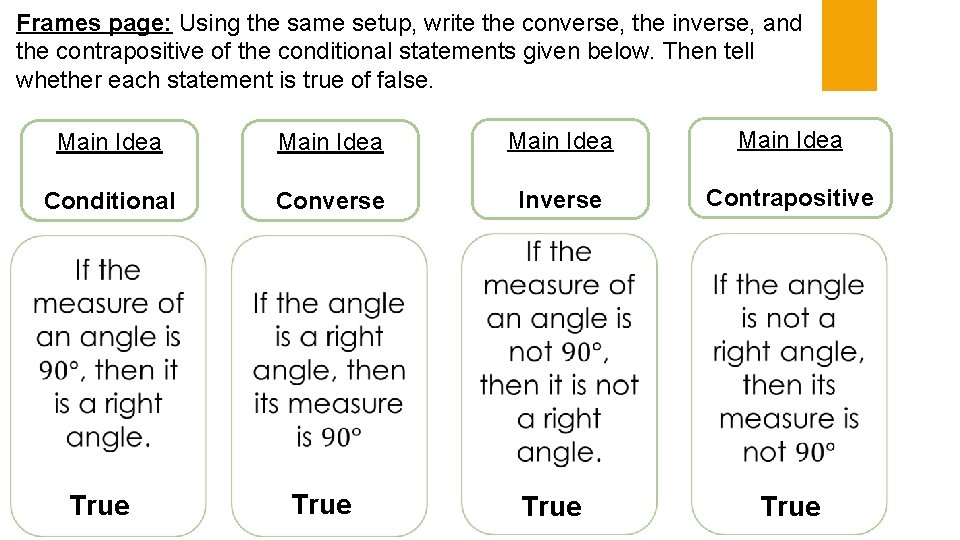
Frames page: Using the same setup, write the converse, the inverse, and the contrapositive of the conditional statements given below. Then tell whether each statement is true of false. Main Idea Conditional Converse Inverse Contrapositive False True

Frames page: Using the same setup, write the converse, the inverse, and the contrapositive of the conditional statements given below. Then tell whether each statement is true of false. Main Idea Conditional Converse Inverse Contrapositive True

Equivalent Statements Based off your findings from examples 1 -3, can you make a conjecture about how each of the statements ended up being true or false? You should have noticed that the and its Conditional statement Contrapositive are either both true or both false. Also, both the Converseand the In general, when two statements are both true or false, they are called Equivalent Statements. Inverse are either both true or both false.

Biconditional Statements

HW 2 -2 Pg. 74 – 76 #’s 1 -5, 7 -13, 19 -29 (EC) 16 -18