Geometry Chapter 10 10 2 FIND ARC MEASURES














- Slides: 33

Geometry Chapter 10 10 -2: FIND ARC MEASURES

Find Arc Measures Objective: Students will be able to use angle measures to find measures for arcs of circles. Agenda Central Angle Arcs Measures of Arcs Congruent Arcs

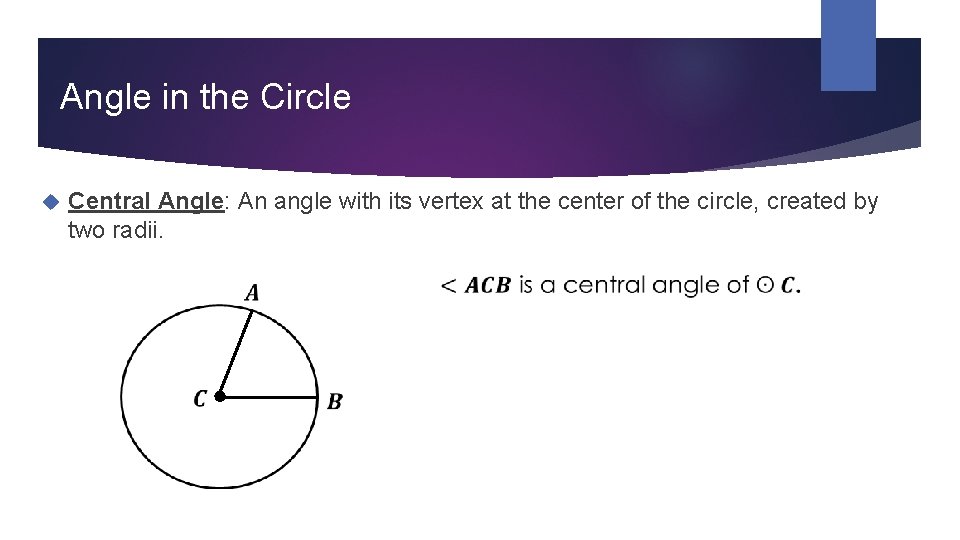
Angle in the Circle Central Angle: An angle with its vertex at the center of the circle, created by two radii.

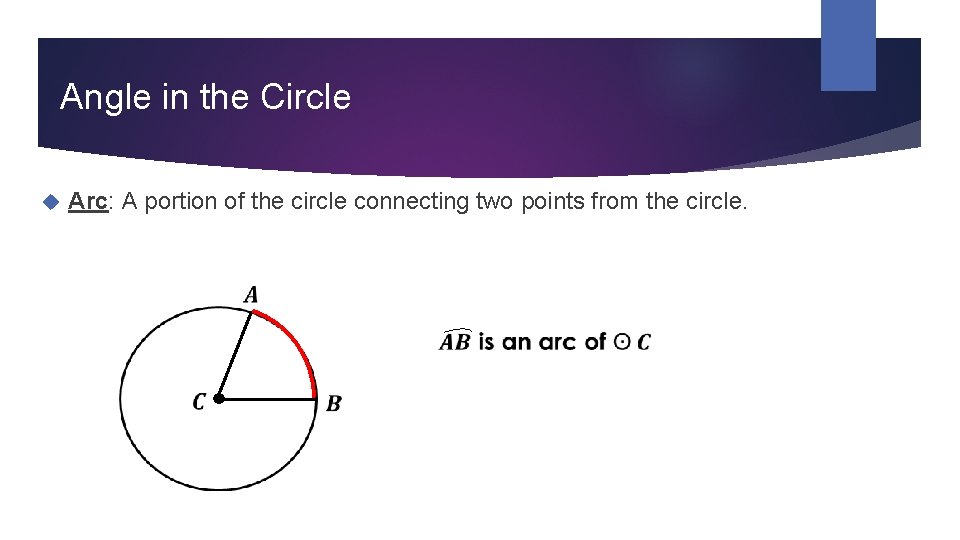
Angle in the Circle Arc: A portion of the circle connecting two points from the circle.

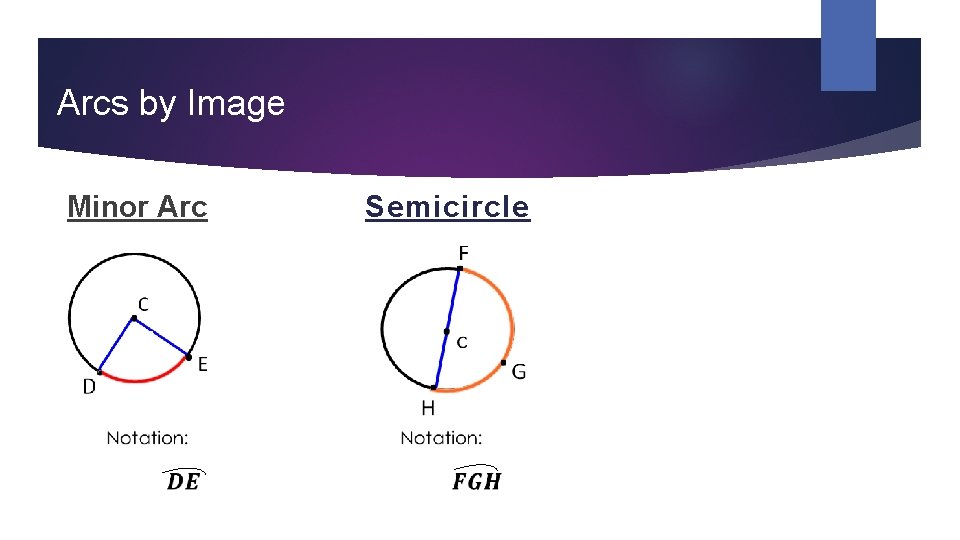
Types of Arcs Minor Arc: The shortest arc connecting two points.

Arcs by Image Minor Arc

Types of Arcs Minor Arc: The shortest arc connecting two points. Semicircle: An arc that connects two points on opposite sides of the circle (i. e. the points of the diameter).

Arcs by Image Minor Arc Semicircle

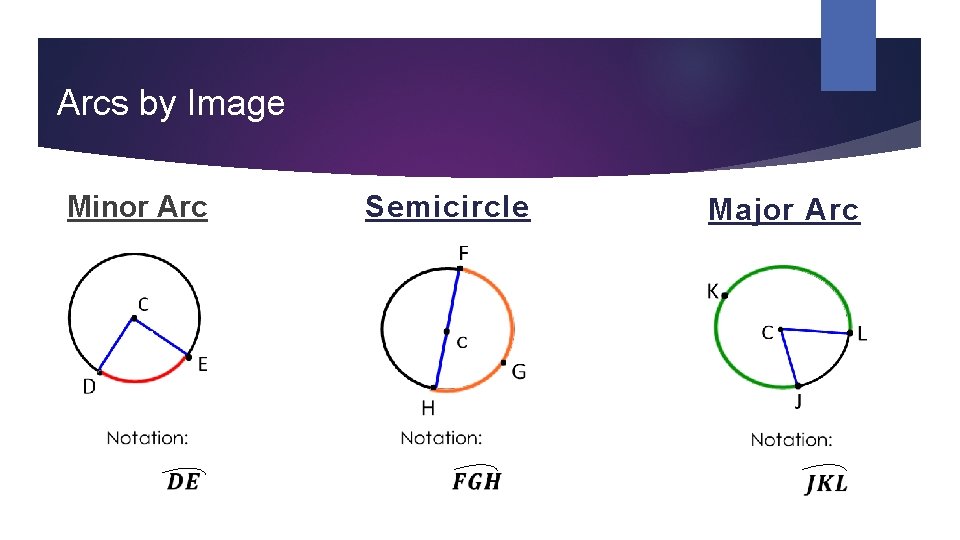
Types of Arcs Minor Arc: The shortest arc connecting two points. Semicircle: An arc that connects two points on opposite sides of the circle (i. e. the points of the diameter). Major Arc: The longest arc connecting two points.

Arcs by Image Minor Arc Semicircle Major Arc

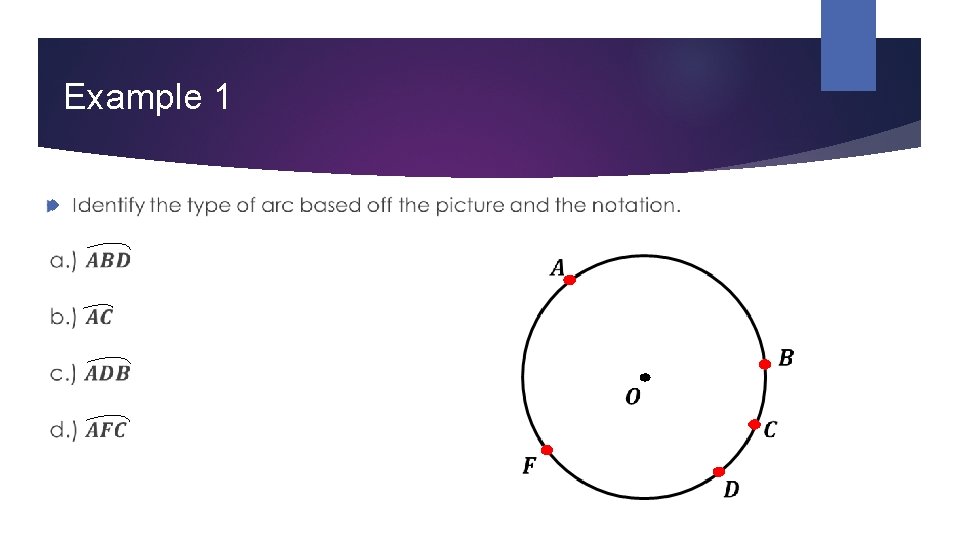
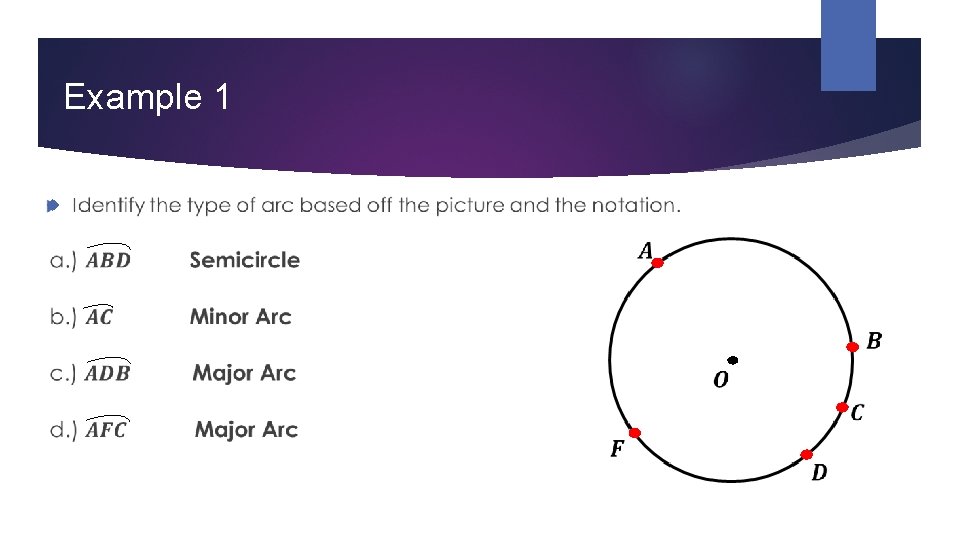
Example 1

Example 1

Measures of the Arcs Example

Measures of the Arcs Example

Measures of the Arcs Example

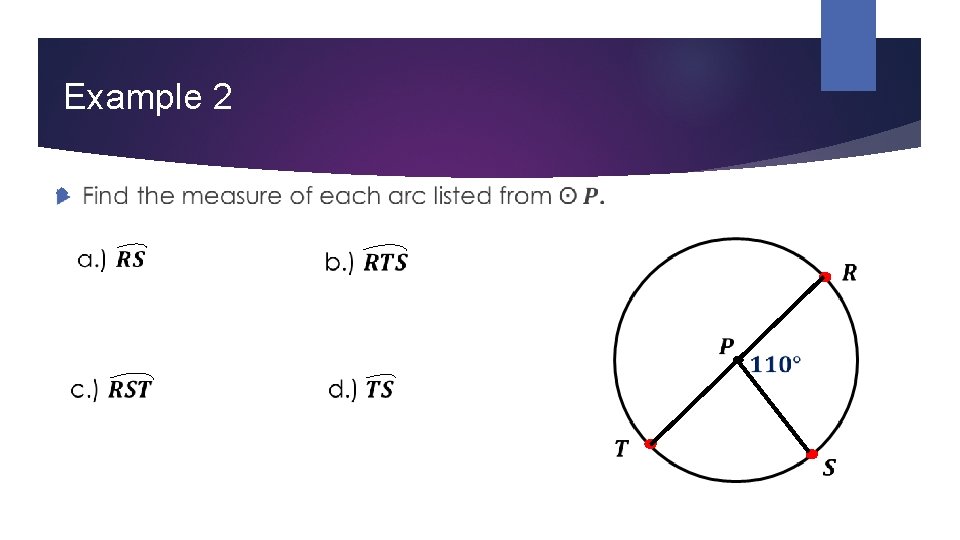
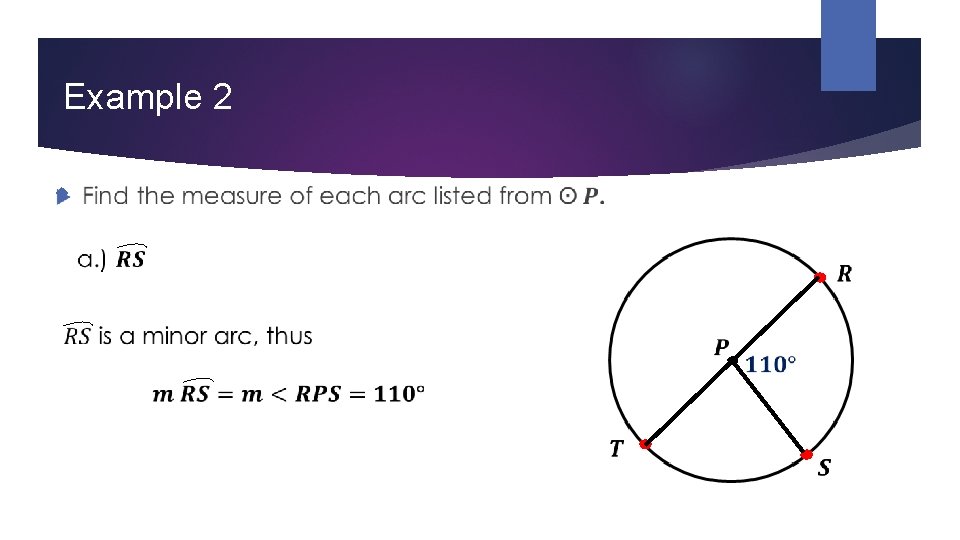
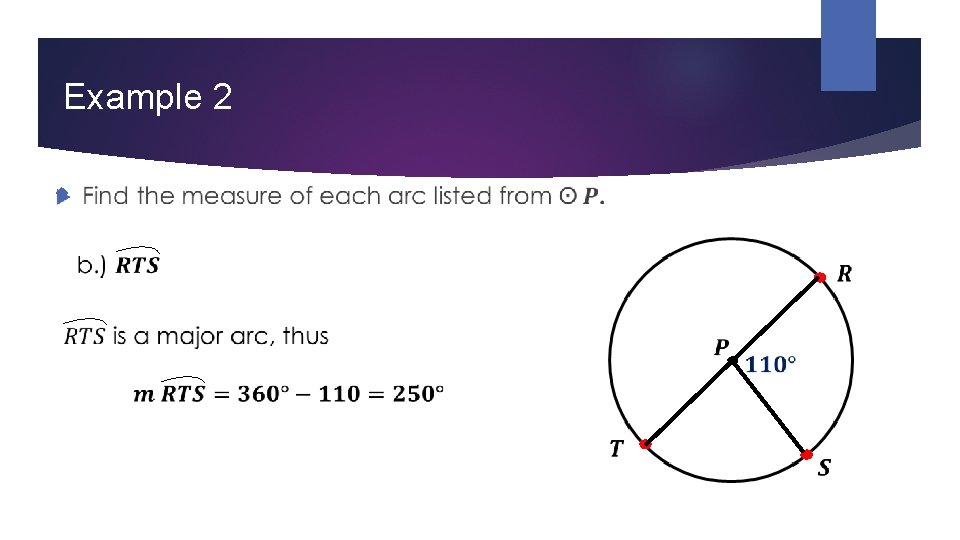
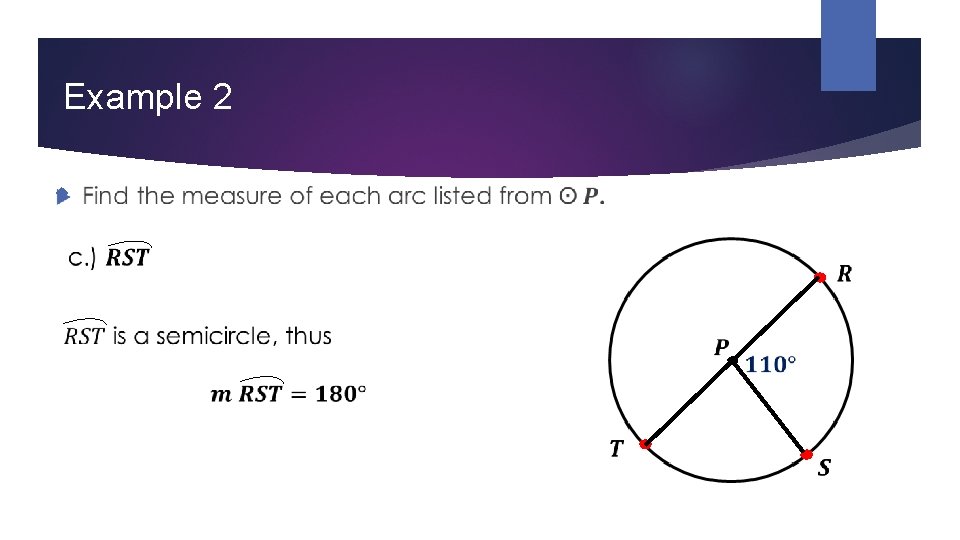
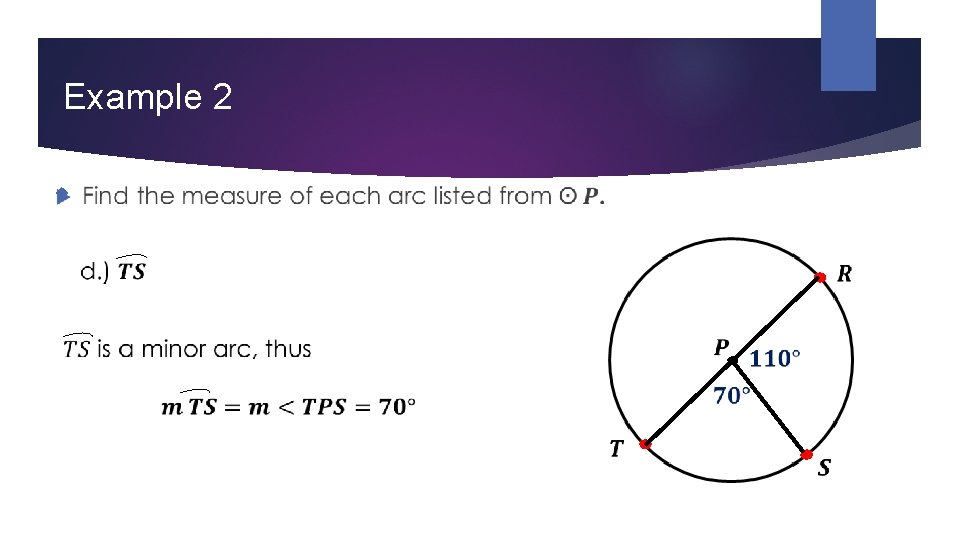
Example 2

Example 2

Example 2

Example 2

Example 2

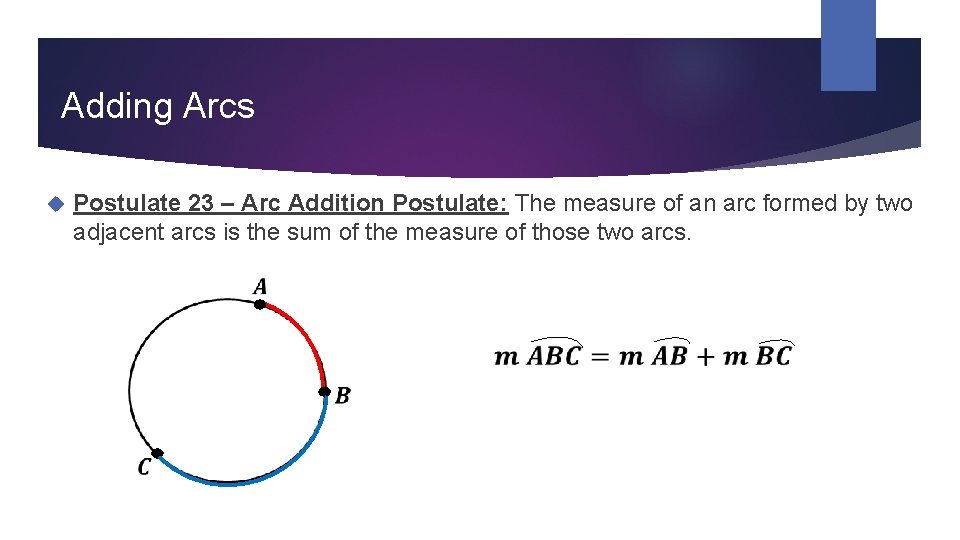
Adding Arcs Postulate 23 – Arc Addition Postulate: The measure of an arc formed by two adjacent arcs is the sum of the measure of those two arcs.

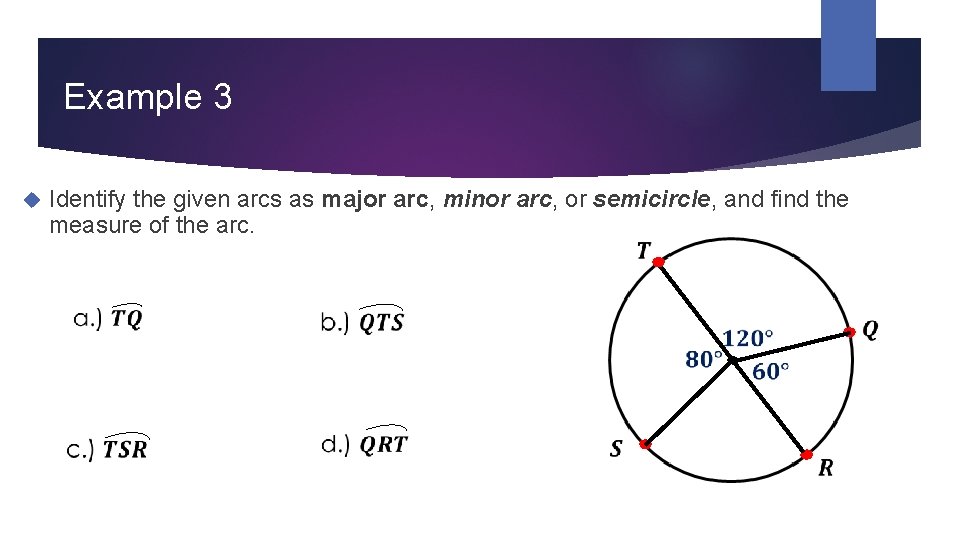
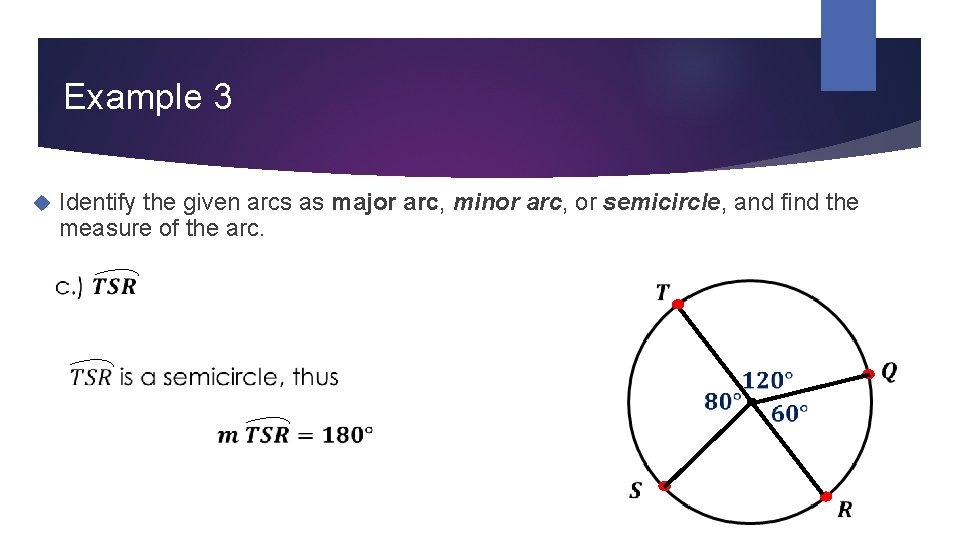
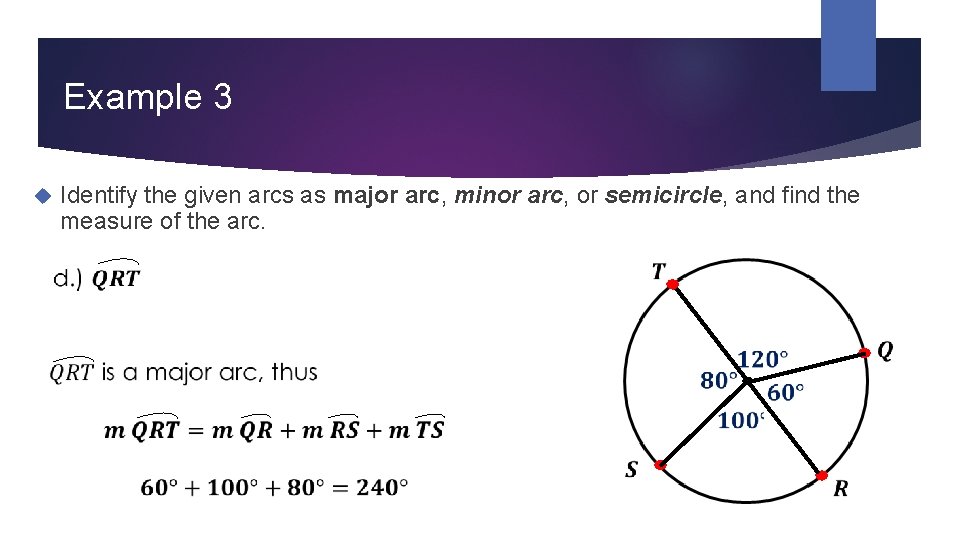
Example 3 Identify the given arcs as major arc, minor arc, or semicircle, and find the measure of the arc.

Example 3 Identify the given arcs as major arc, minor arc, or semicircle, and find the measure of the arc.

Example 3 Identify the given arcs as major arc, minor arc, or semicircle, and find the measure of the arc.

Example 3 Identify the given arcs as major arc, minor arc, or semicircle, and find the measure of the arc.

Example 3 Identify the given arcs as major arc, minor arc, or semicircle, and find the measure of the arc.

Congruent Arcs Circles are congruent if they have the same radius. Two arcs are congruent arcs if they have the same measure and they are arcs of the same circle, or if they are arcs of congruent circles.

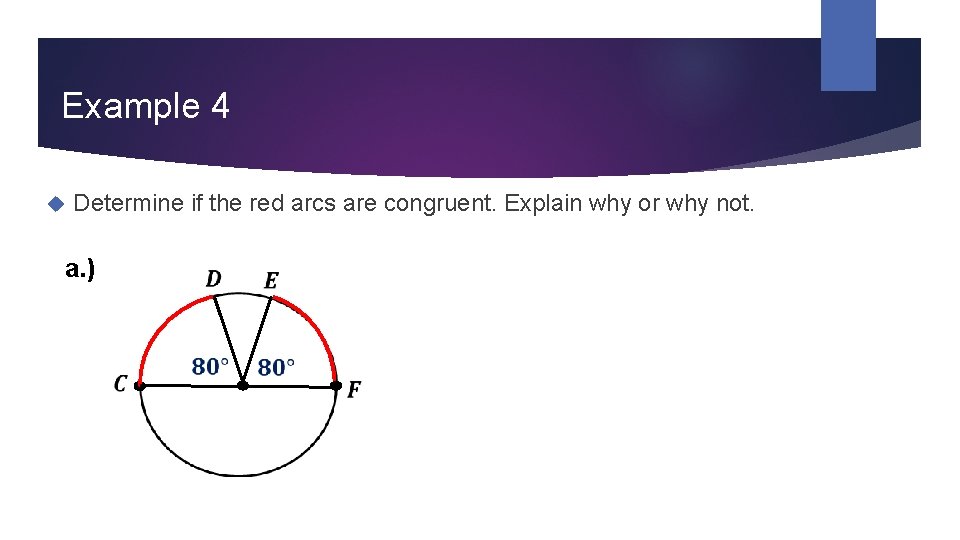
Example 4 Determine if the red arcs are congruent. Explain why or why not. a. )

Example 4 Determine if the red arcs are congruent. Explain why or why not. a. )

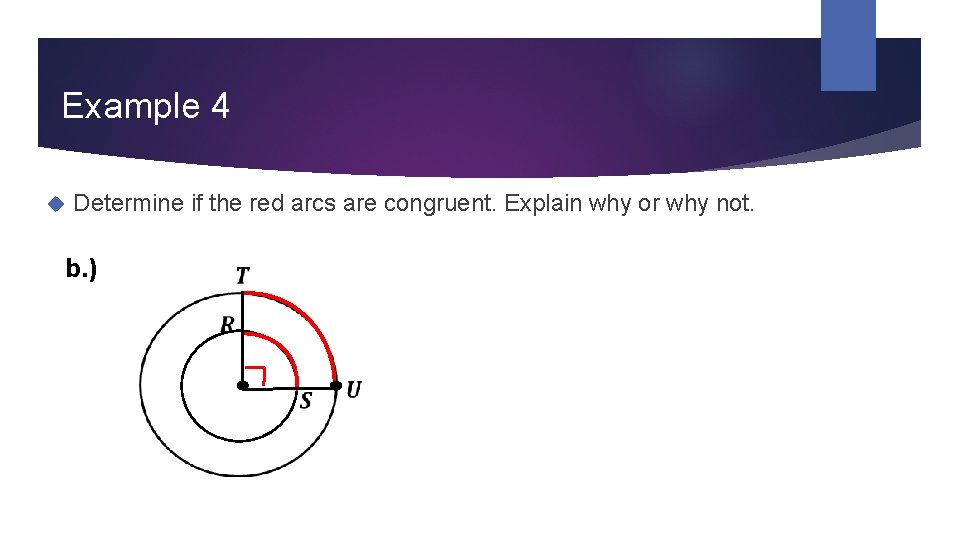
Example 4 Determine if the red arcs are congruent. Explain why or why not. b. )

Example 4 Determine if the red arcs are congruent. Explain why or why not. b. )

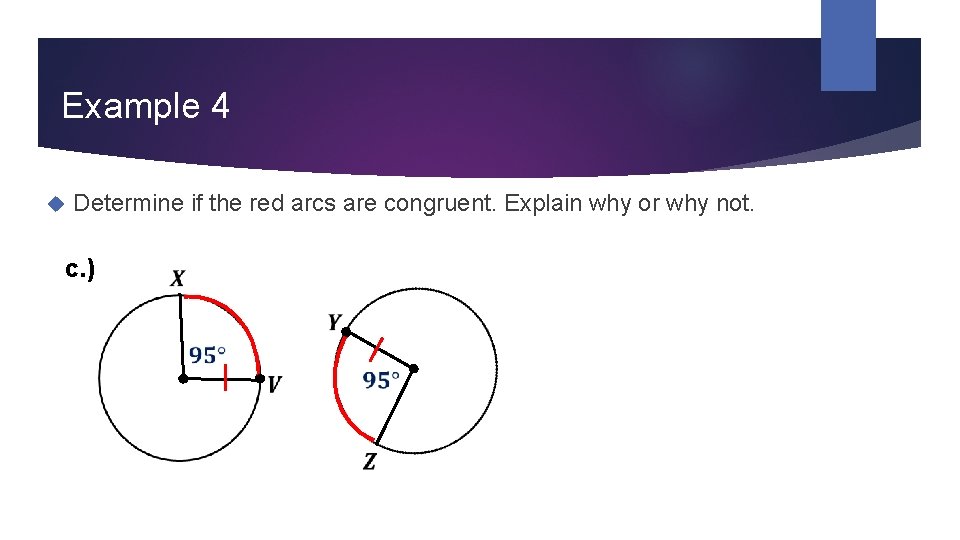
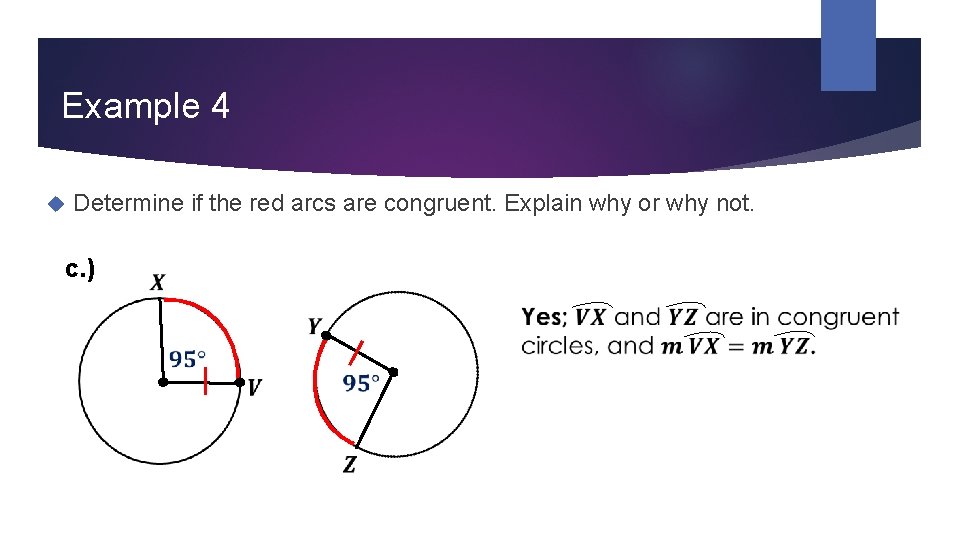
Example 4 Determine if the red arcs are congruent. Explain why or why not. c. )

Example 4 Determine if the red arcs are congruent. Explain why or why not. c. )