GEOMETRY Area Surface Area Perimeter Volume Area The

GEOMETRY Area, Surface Area, Perimeter, Volume

Area • The number of square units to cover the surface of a geometric figure • Think: covering the floor of a room with carpet • Different area formulas for different shapes A = 100 sq. units • Always written in terms of units squared or square units (units 2)

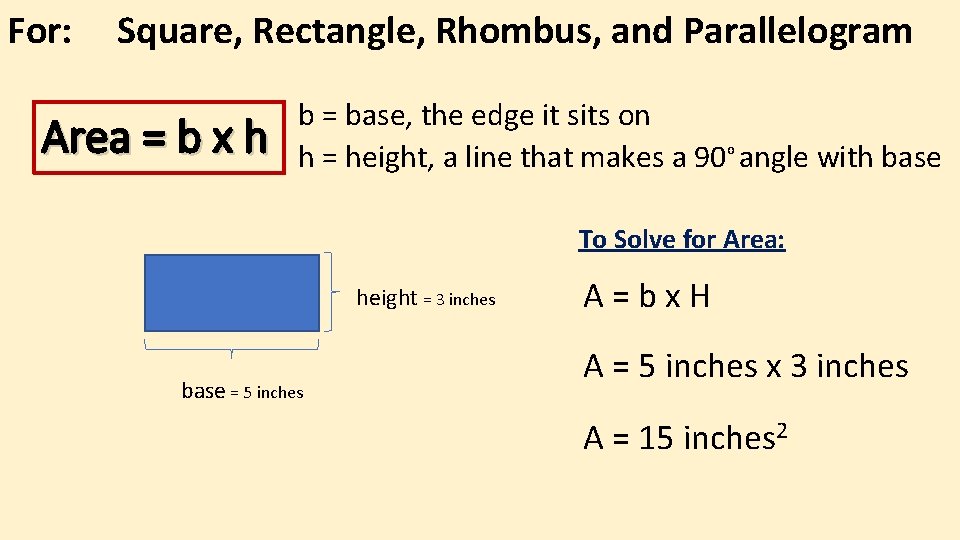
For: Square, Rectangle, Rhombus, and Parallelogram Area = b x h b = base, the edge it sits on h = height, a line that makes a 90 o angle with base To Solve for Area: height = 3 inches base = 5 inches A=bx. H A = 5 inches x 3 inches A = 15 inches 2

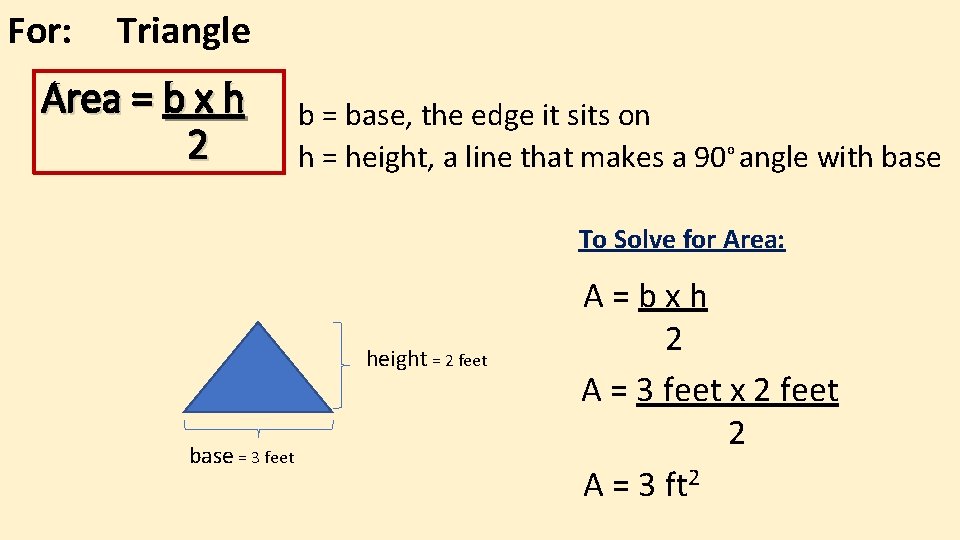
For: Triangle Area = b x h 2 b = base, the edge it sits on h = height, a line that makes a 90 o angle with base To Solve for Area: height = 2 feet base = 3 feet A=bxh 2 A = 3 feet x 2 feet 2 A = 3 ft 2

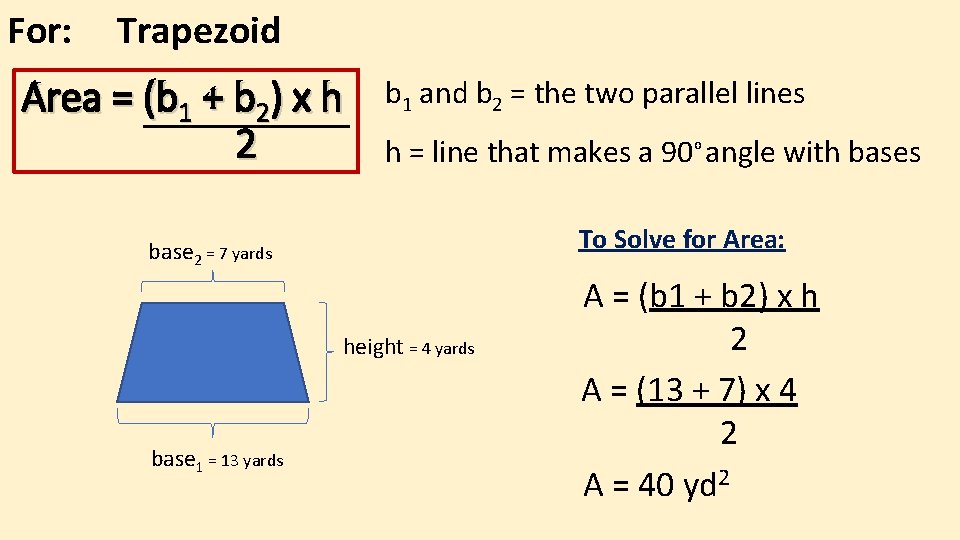
For: Trapezoid Area = (b 1 + b 2) x h 2 b 1 and b 2 = the two parallel lines h = line that makes a 90 o angle with bases To Solve for Area: base 2 = 7 yards height = 4 yards base 1 = 13 yards A = (b 1 + b 2) x h 2 A = (13 + 7) x 4 2 A = 40 yd 2

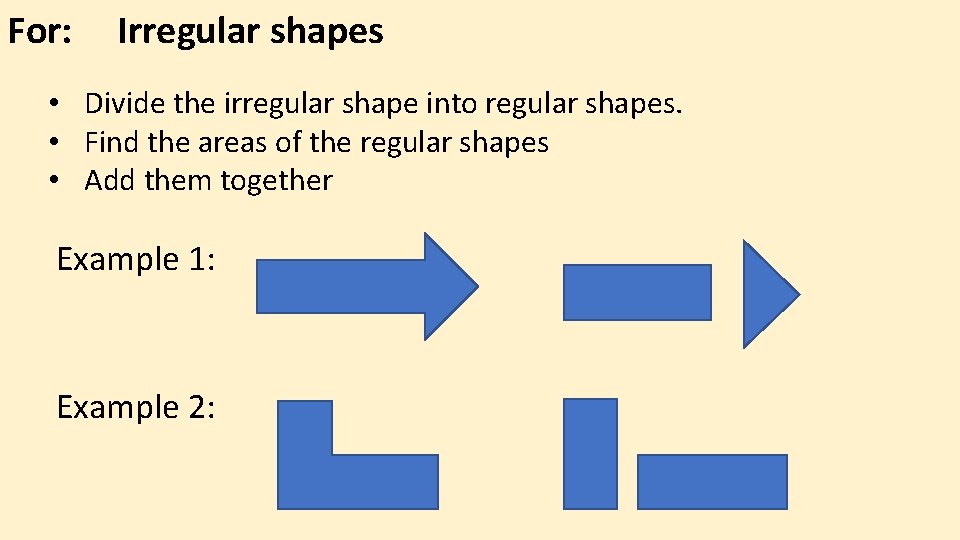
For: Irregular shapes • Divide the irregular shape into regular shapes. • Find the areas of the regular shapes • Add them together Example 1: Example 2:

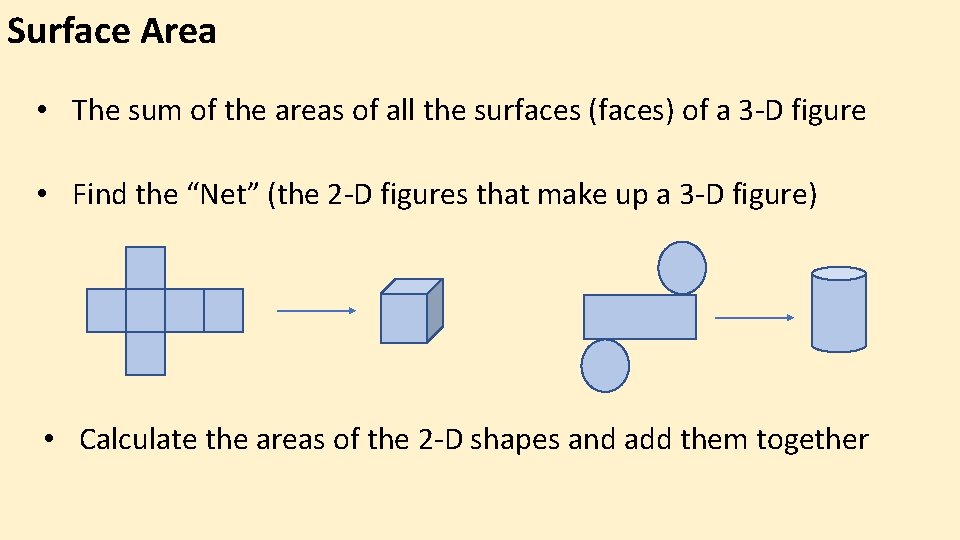
Surface Area • The sum of the areas of all the surfaces (faces) of a 3 -D figure • Find the “Net” (the 2 -D figures that make up a 3 -D figure) • Calculate the areas of the 2 -D shapes and add them together

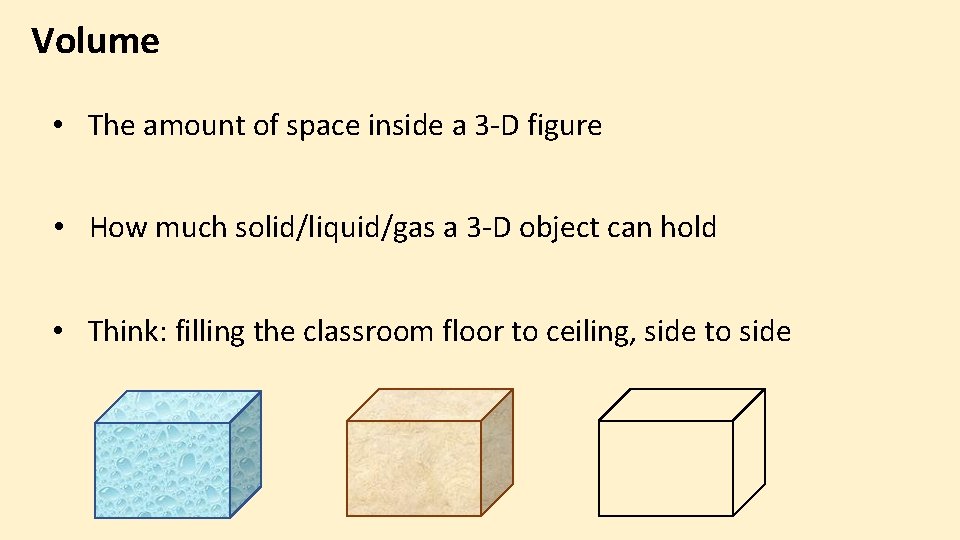
Volume • The amount of space inside a 3 -D figure • How much solid/liquid/gas a 3 -D object can hold • Think: filling the classroom floor to ceiling, side to side

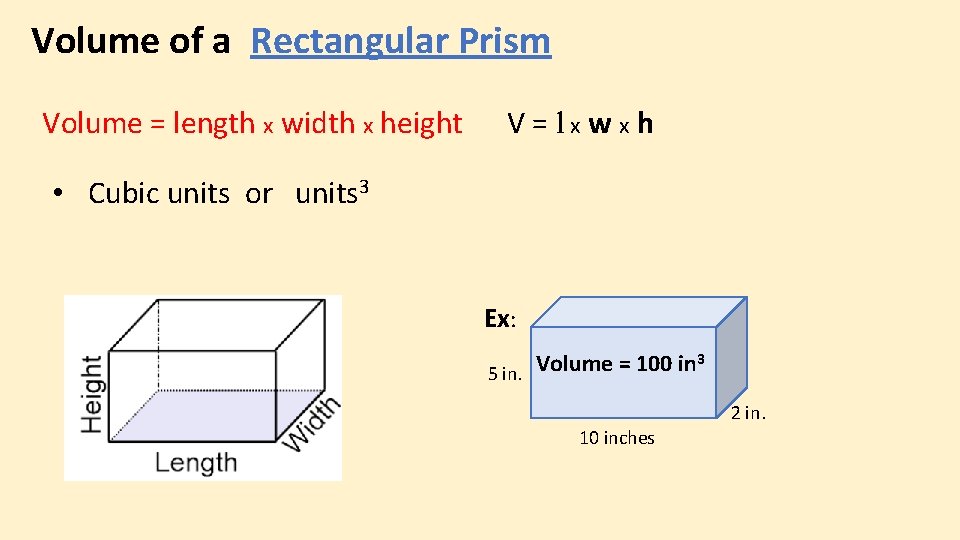
Volume of a Rectangular Prism Volume = length x width x height V=lxwxh • Cubic units or units 3 Ex: 5 in. Volume = 100 in 3 2 in. 10 inches

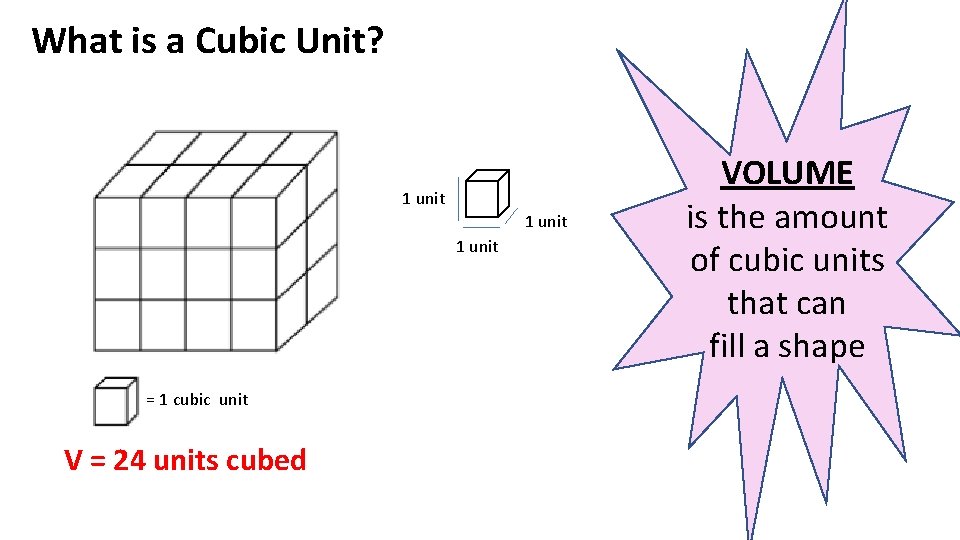
What is a Cubic Unit? 1 unit = 1 cubic unit V = 24 units cubed VOLUME is the amount of cubic units that can fill a shape

Practice EX 1: EX 2: EX 3: 5. 5 yds 4 ft 14 yards 3 yds 2 ft 3 ft V = 24 feet 3 V = 231 yards 3 V = 1 inch 3