Geometry 9 5 Inscribed Angles Inscribed Angles The

Geometry 9. 5 Inscribed Angles

Inscribed Angles The vertex is on the circle n The sides of the angle: n § Are chords of the circle § Intercept an arc on the circle Inscribed angle Intercepted Arc

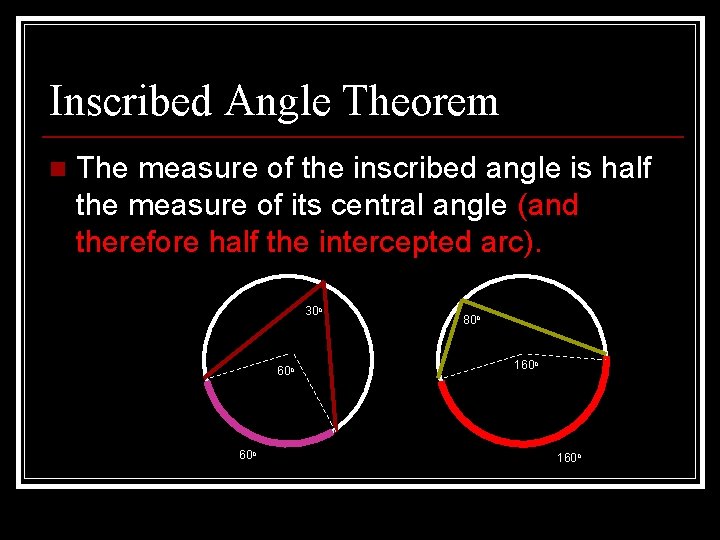
Inscribed Angle Theorem n The measure of the inscribed angle is half the measure of its central angle (and therefore half the intercepted arc). 30 o 60 o 80 o 160 o

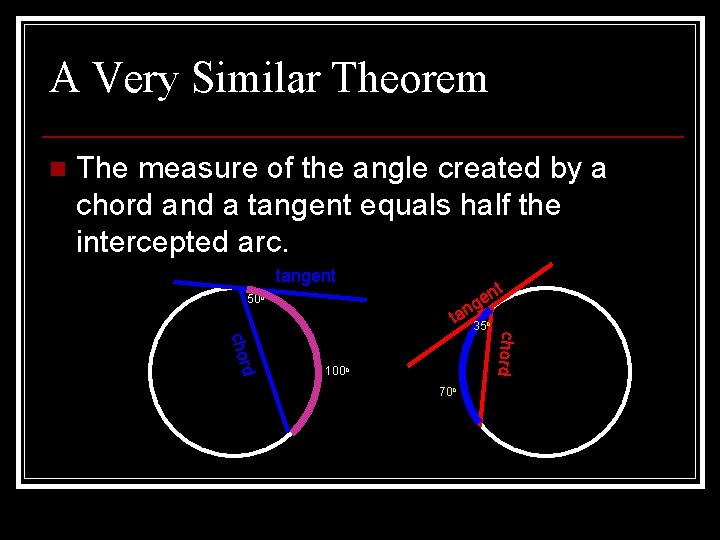
A Very Similar Theorem n The measure of the angle created by a chord and a tangent equals half the intercepted arc. tangent 50 o d chord nt e g n a t 35 o 100 o 70 o

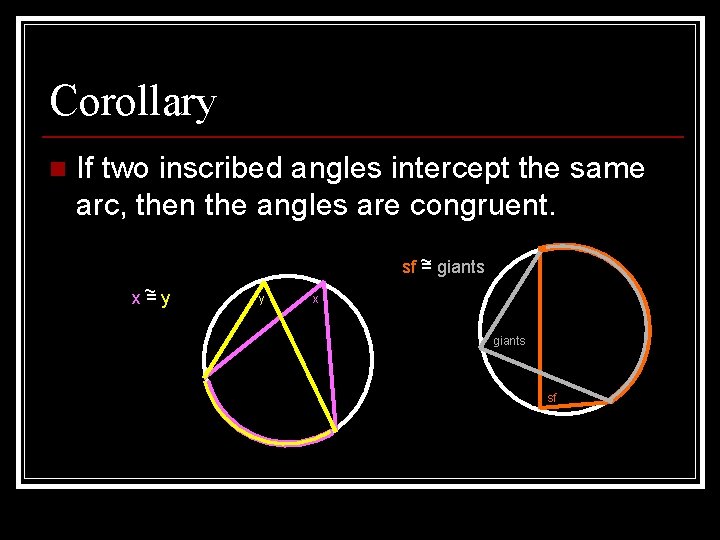
Corollary n If two inscribed angles intercept the same arc, then the angles are congruent. ~ giants sf = x~ =y y x giants sf

Corollary n If an inscribed angle intercepts a semicircle, then it is a right angle. Why? 180 o eter diam 90 o

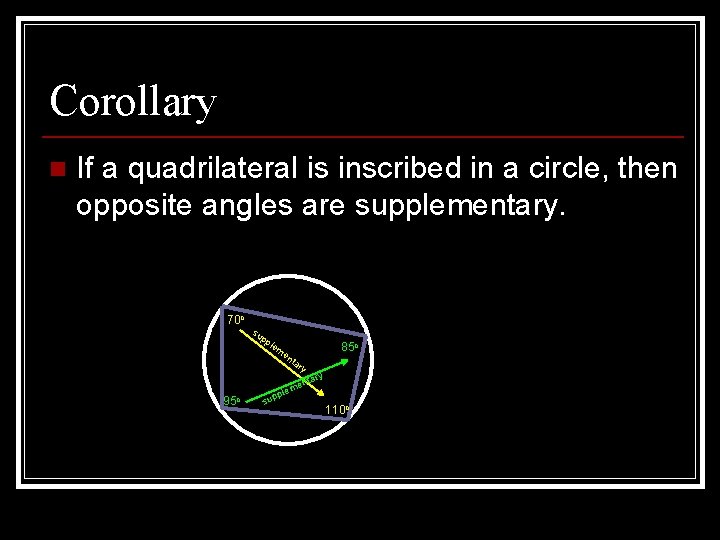
Corollary n If a quadrilateral is inscribed in a circle, then opposite angles are supplementary. 70 o su pp lem 85 o en ta 95 o ry ary nt me ple sup 110 o

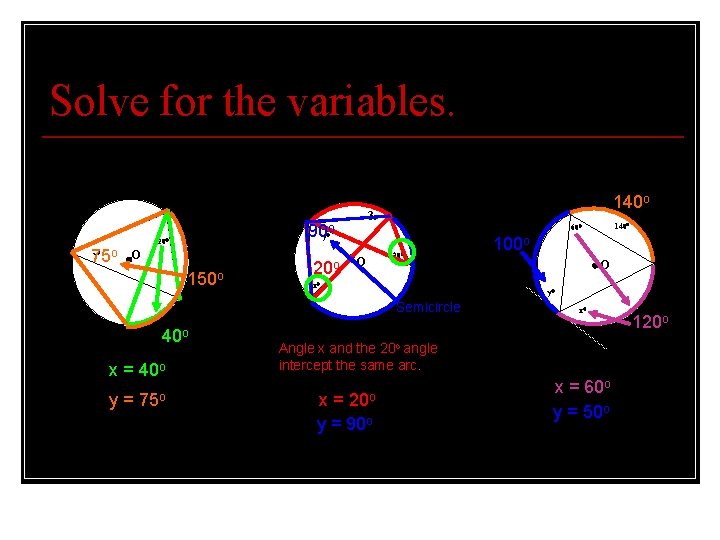
Solve for the variables. 1. 140 o 2. 75 o y 3. 90 o 20 110 O 150 o 20 o O 20 x 40 o x = 40 o y = 75 o 100 o O y Semicircle x 140 60 y x Angle x and the 20 o angle intercept the same arc. x = 20 o y = 90 o x = 60 o y = 50 o 120 o

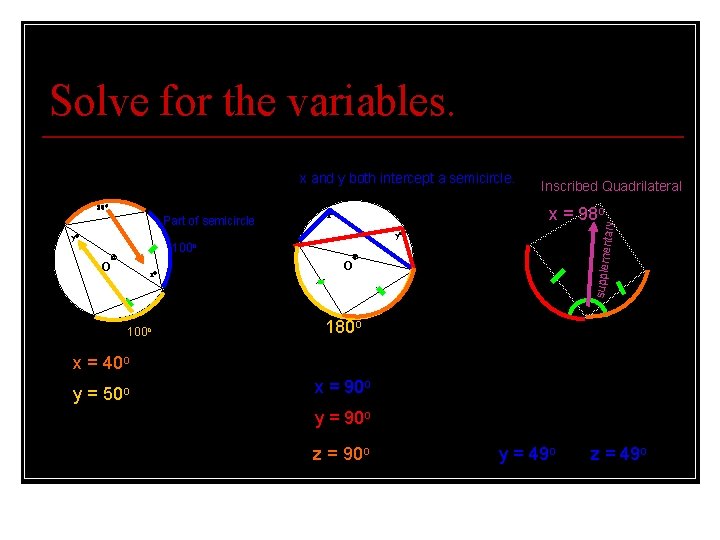
Solve for the variables. 5. 80 Part of semicircle x and y both intercept a semicircle. 6. x = 98 x o x y y 100 o O x O O z 100 o 180 o x = 40 o y= Inscribed Quadrilateral 50 o y suppleme ntary 4. 82 z y + 82 o + z = 180 o y + z = 98 o x = 90 o y = 90 o z = 90 o The red and orange arcs are congruent (they have congruent chords). Thus, y and z are congruent angles (they intercept the red and orange arcs). y = 49 o z = 49 o

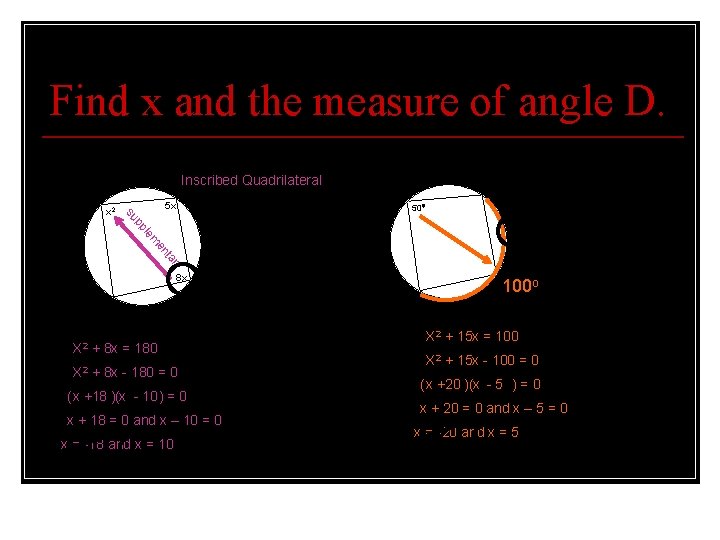
Find x and the measure of angle D. 7. Inscribed Quadrilateral A 5 x B 4 x A B 50 pp su x 2 8. If x is negative, this angle would have a negative value. ry ta en m le 15 x 8 x D X 2 + 8 x = 180 X 2 + 8 x - 180 = 0 If x is negative, this angle would have a negative value. ( x +18 )(x - 10 ) = 0 x + 18 = 0 and x – 10 = 0 x = -18 and x = 10 C 100 o C D x 2 X 2 + 15 x = 100 X 2 + 15 x - 100 = 0 ( x +20 )(x - 5 ) = 0 x + 20 = 0 and x – 5 = 0 x = -20 and x = 5

HW