Geometry 8 1 Right Triangles A radical is

  • Slides: 19
Download presentation
Geometry 8. 1 Right Triangles

Geometry 8. 1 Right Triangles

A radical is in simplest form when: 1. No perfect square factor other than

A radical is in simplest form when: 1. No perfect square factor other than 1 is under the radical sign. 2. No fraction is under the radical sign. 3. No radical is in a denominator. Simplify: Answers: #2 and #4 Together…You got the rest!!

Geometric Mean If a, b and x are positive numbers and mean then x

Geometric Mean If a, b and x are positive numbers and mean then x is called the geometric mean between a and b. Multiplying means/extremes we find that: Taking the square root of each side: A positive number

Geometric Mean • Basically, to find the geometric mean of 2 numbers, multiply them

Geometric Mean • Basically, to find the geometric mean of 2 numbers, multiply them and take the square root. OR (add to notes: take the square root of each, then multiply try to find the geometric mean between 4 and 9 and the geometric mean between 36 and 50) • Note that the geometric mean always falls between the 2 numbers. Ex: Find the geometric mean between 5 and 11. Use the formula

Geometric Mean Ex: Find the geometric mean between the two numbers. a. 5 and

Geometric Mean Ex: Find the geometric mean between the two numbers. a. 5 and 20 Avoid multiplying large numbers together. Break numbers into perfect square factors to simplify. b. 24 and 32

Directions: Find the geometric mean between the two numbers. 8. 64 and 49 9.

Directions: Find the geometric mean between the two numbers. 8. 64 and 49 9. 1 and 3 10. 100 and 6 11. 20 and 24

Geometric Mean Find the geometric mean between the two numbers. 7. 5 and 20

Geometric Mean Find the geometric mean between the two numbers. 7. 5 and 20 8. 64 and 49 9. 1 and 3 10. 100 and 6 11. 20 and 24

∆ Review Hypotenuse the side opposite the right angle in a right triangle •

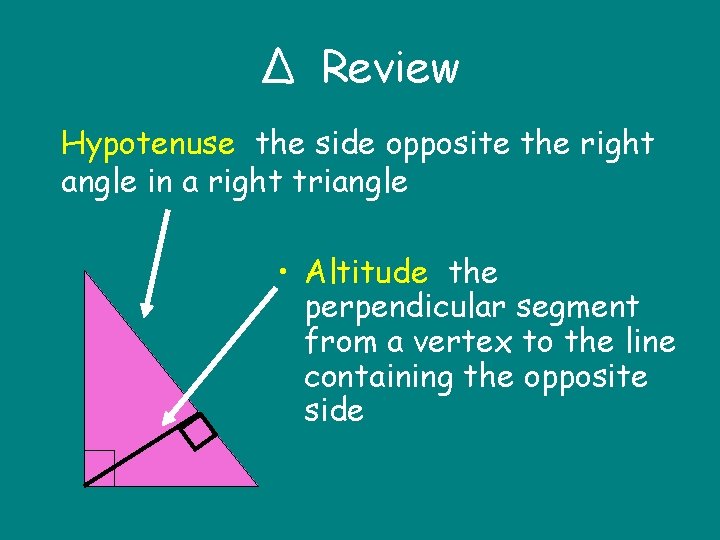
∆ Review Hypotenuse the side opposite the right angle in a right triangle • Altitude the perpendicular segment from a vertex to the line containing the opposite side

Theorem If the altitude is drawn to the hypotenuse of a right triangle, then

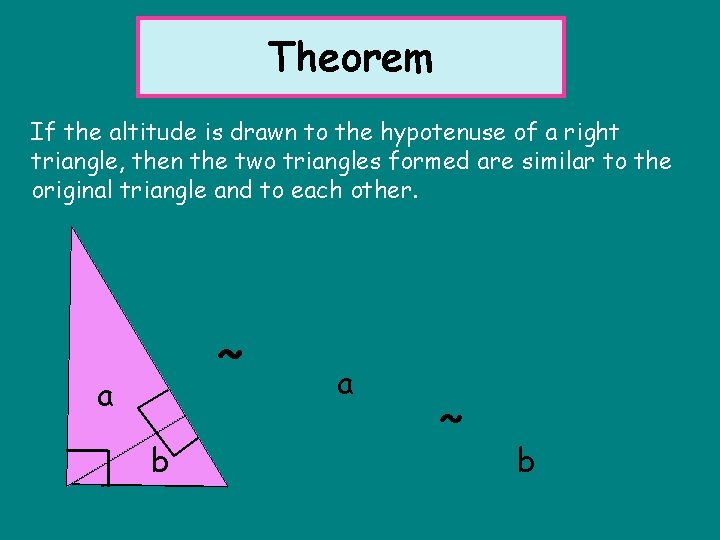
Theorem If the altitude is drawn to the hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and to each other. ~ a b a ~ b

Corollaries When the altitude is drawn to the hypotenuse of a right triangle: Y

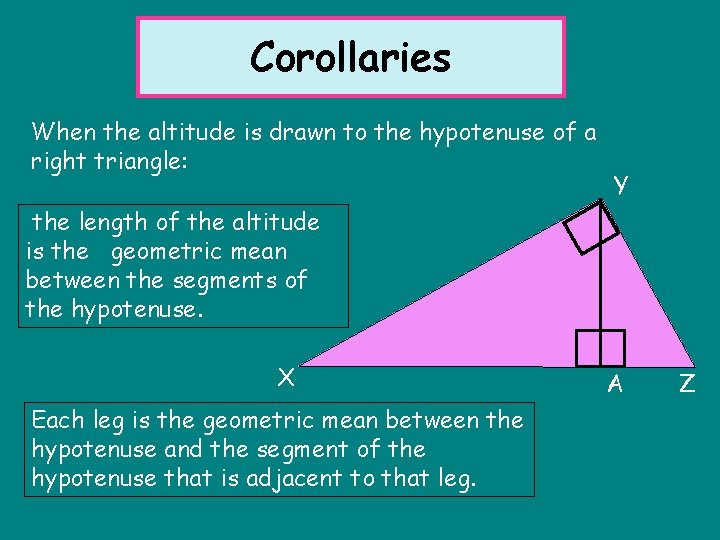
Corollaries When the altitude is drawn to the hypotenuse of a right triangle: Y the length of the altitude is the geometric mean between the segments of the hypotenuse. X Each leg is the geometric mean between the hypotenuse and the segment of the hypotenuse that is adjacent to that leg. A Z

Corollary 1 piece of hypotenuse altitude X altitude = other piece of hypotenuse Y

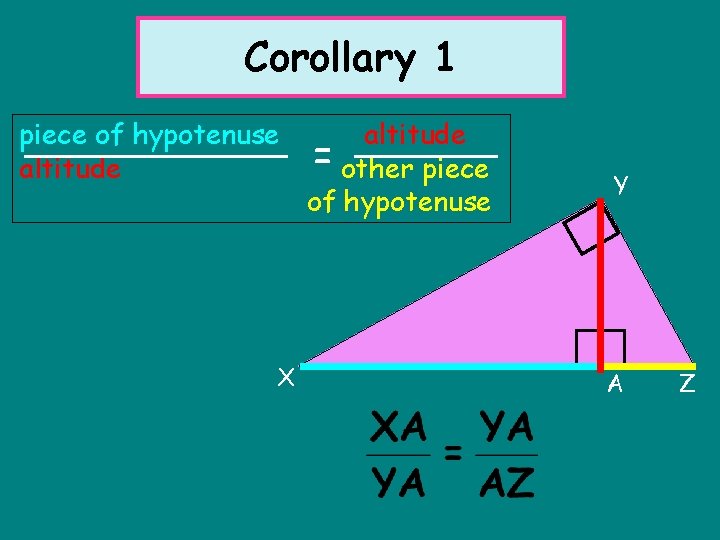
Corollary 1 piece of hypotenuse altitude X altitude = other piece of hypotenuse Y A Z

Corollary 2 hypotenuse leg piece of hyp. adj. to leg = X Y A

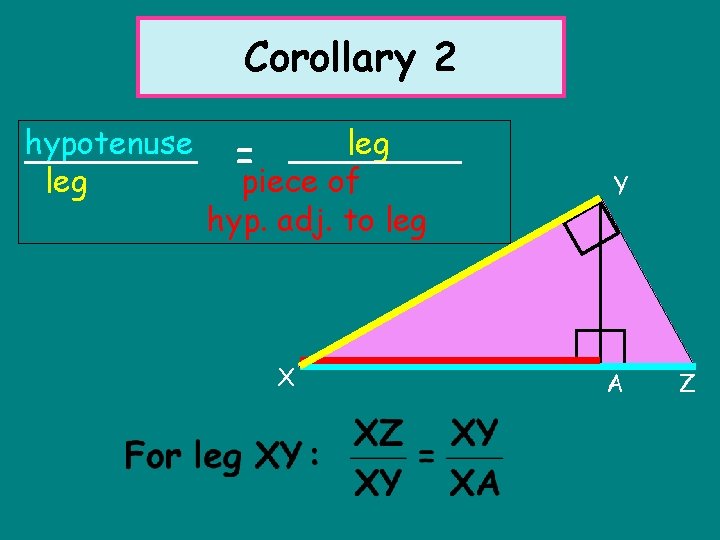
Corollary 2 hypotenuse leg piece of hyp. adj. to leg = X Y A Z

Corollary 2 hypotenuse leg piece of hyp. adj. to leg = X Y A

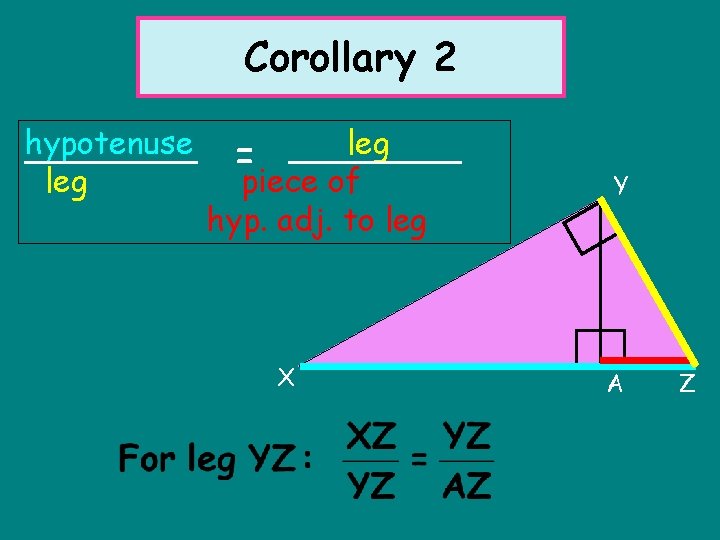
Corollary 2 hypotenuse leg piece of hyp. adj. to leg = X Y A Z

Directions: Exercises 24 -31 refer to the diagram at right. 12. If CN =

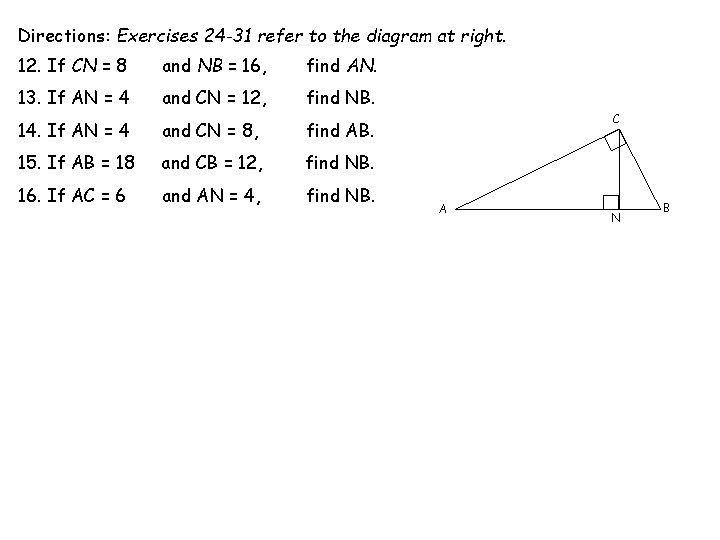
Directions: Exercises 24 -31 refer to the diagram at right. 12. If CN = 8 and NB = 16, find AN. 13. If AN = 4 and CN = 12, find NB. 14. If AN = 4 and CN = 8, find AB. 15. If AB = 18 and CB = 12, find NB. 16. If AC = 6 and AN = 4, find NB. C A N B

Homework pg. 288 #16 -30, 31 -39 odd

Homework pg. 288 #16 -30, 31 -39 odd

Exercises C 8 A x 12. If CN = 8 and NB = 16,

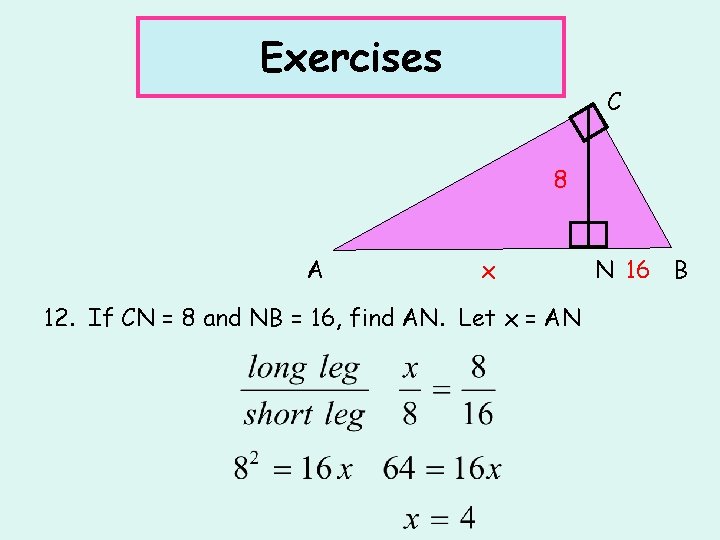
Exercises C 8 A x 12. If CN = 8 and NB = 16, find AN. Let x = AN N 16 B

Exercises C x A 8 14. If AN = 8 and NB = 12,

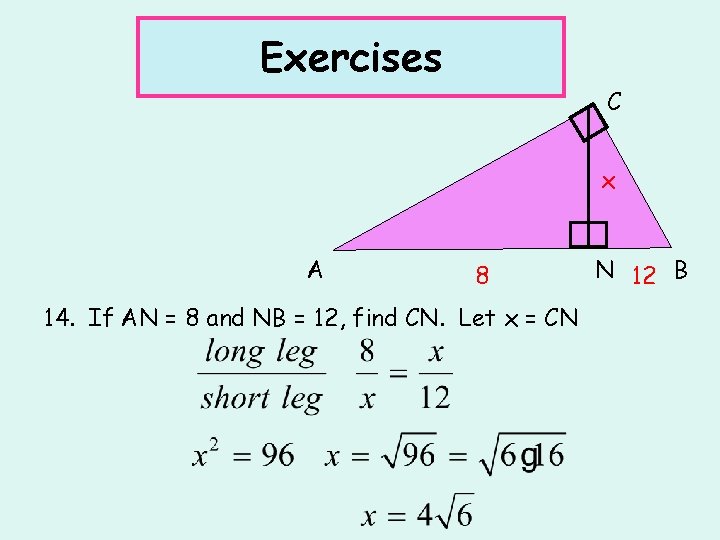
Exercises C x A 8 14. If AN = 8 and NB = 12, find CN. Let x = CN N 12 B

Exercises C 12 N x 18 17. If AB = 18 and CB =

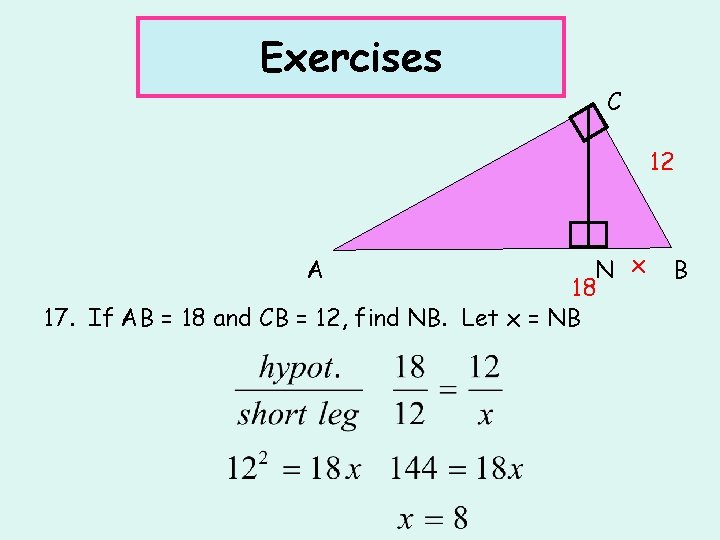
Exercises C 12 N x 18 17. If AB = 18 and CB = 12, find NB. Let x = NB A B

Answers Exercises 13 - 19 13. 15. 16. 18. 19. 36 20 2√ 15

Answers Exercises 13 - 19 13. 15. 16. 18. 19. 36 20 2√ 15 25 5

RADICAL Are you a Radical RADICAL RADICAL StormsRADICAL Are you a Radical RADICAL RADICAL Storms
LESSON EIGHTEEN SPECIAL RIGHT TRIANGLES SPECIAL RIGHT TRIANGLESLESSON EIGHTEEN SPECIAL RIGHT TRIANGLES SPECIAL RIGHT TRIANGLES
Right Triangles Right Triangles n A triangle withRight Triangles Right Triangles n A triangle with
45 45 90 right triangles Some right triangles45 45 90 right triangles Some right triangles
45 45 90 right triangles Some right triangles45 45 90 right triangles Some right triangles
Special Right Triangles What are Special Right TrianglesSpecial Right Triangles What are Special Right Triangles
Radical Reconstruction Radical Reconstruction Period when Radical RepublicansRadical Reconstruction Radical Reconstruction Period when Radical Republicans
RADICAL Becoming Radical RADICAL Our lives could becomeRADICAL Becoming Radical RADICAL Our lives could become
Special Right Triangles Geometry 7 3 Special RightSpecial Right Triangles Geometry 7 3 Special Right
Geometry Unit 5 Jeopardy Special right Triangles RightGeometry Unit 5 Jeopardy Special right Triangles Right
Projective Geometry Projective Geometry Projective Geometry Projective GeometryProjective Geometry Projective Geometry Projective Geometry Projective Geometry
Similar Triangles Identify Similar Triangles Triangles are similarSimilar Triangles Identify Similar Triangles Triangles are similar
SIMILAR TRIANGLES Identify similar triangles Use similar trianglesSIMILAR TRIANGLES Identify similar triangles Use similar triangles
Lesson 4 3 Congruent Triangles Congruent triangles trianglesLesson 4 3 Congruent Triangles Congruent triangles triangles
Similar Triangles When are triangles considered similar TrianglesSimilar Triangles When are triangles considered similar Triangles
Inequalities in Triangles Inequalities in Triangles Triangles haveInequalities in Triangles Inequalities in Triangles Triangles have
4 3 Congruent Triangles Congruent triangles Triangles that4 3 Congruent Triangles Congruent triangles Triangles that
Right Item Right Time Right Place Right PriceRight Item Right Time Right Place Right Price