Geometry 6 3 Medians and Altitudes of Triangles









- Slides: 21

Geometry 6. 3 Medians and Altitudes of Triangles EQ: Do the Centroid and Orthocenters lie inside, outside, or on a triangle?

Goals n n Know what medians and altitudes are. Know what centroids and orthocenters are. Be able to construct centroids and orthocenters. Use centroids to solve problems. 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 2

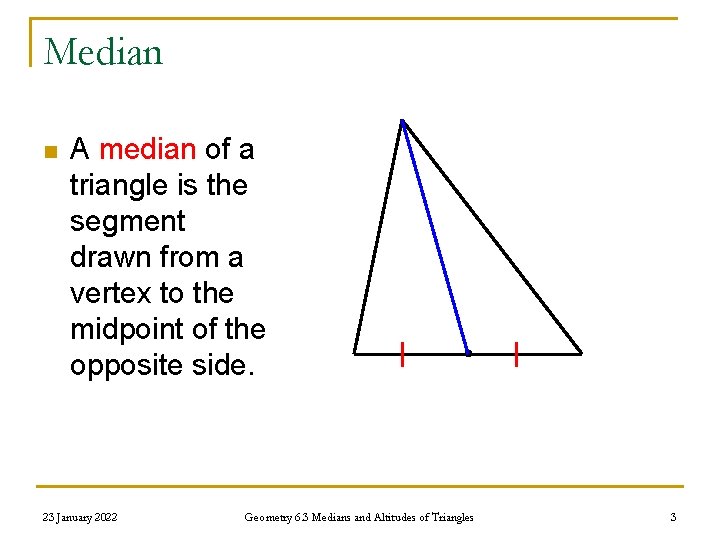
Median n A median of a triangle is the segment drawn from a vertex to the midpoint of the opposite side. 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 3

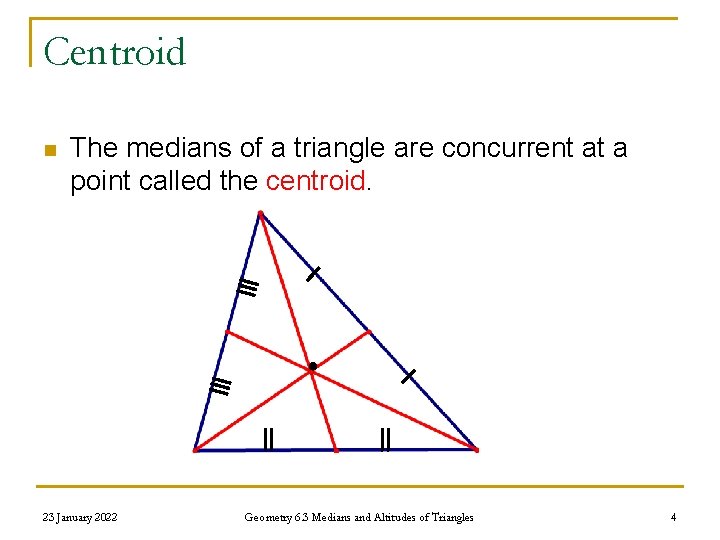
Centroid n The medians of a triangle are concurrent at a point called the centroid. 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 4

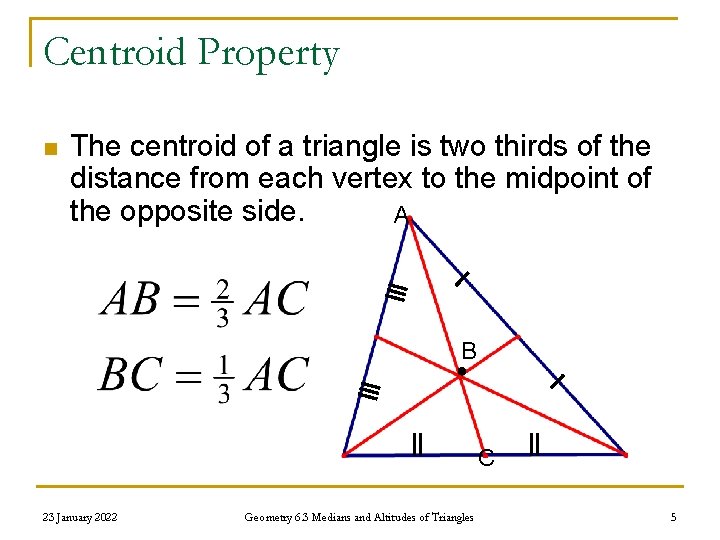
Centroid Property n The centroid of a triangle is two thirds of the distance from each vertex to the midpoint of the opposite side. A B C 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 5

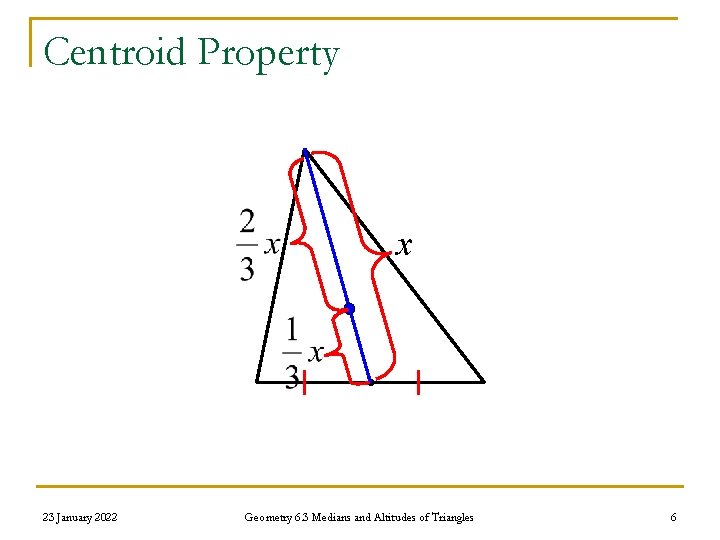
Centroid Property x 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 6

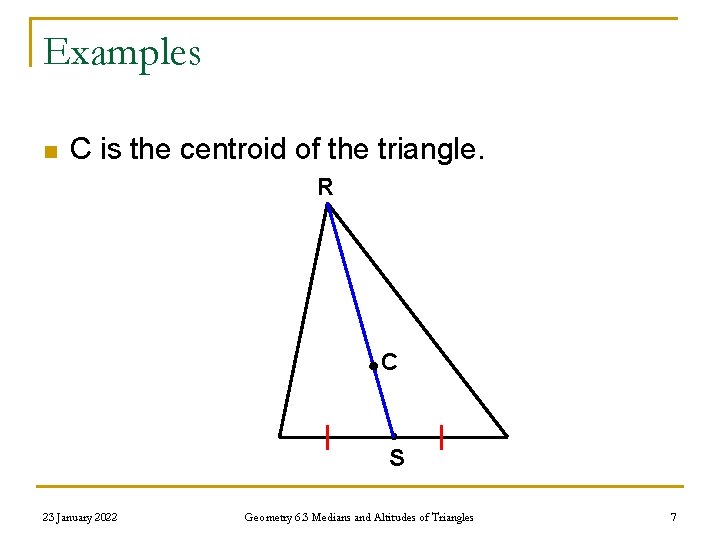
Examples n C is the centroid of the triangle. R C S 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 7

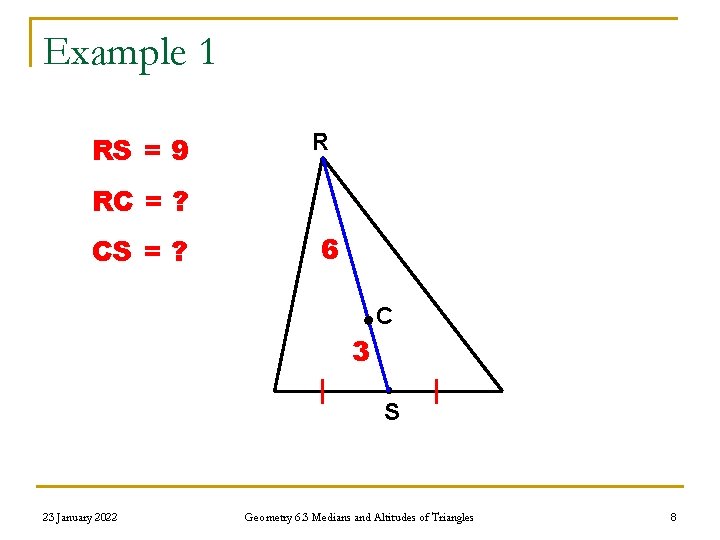
Example 1 RS = 9 R RC = ? CS = ? 6 C 3 S 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 8

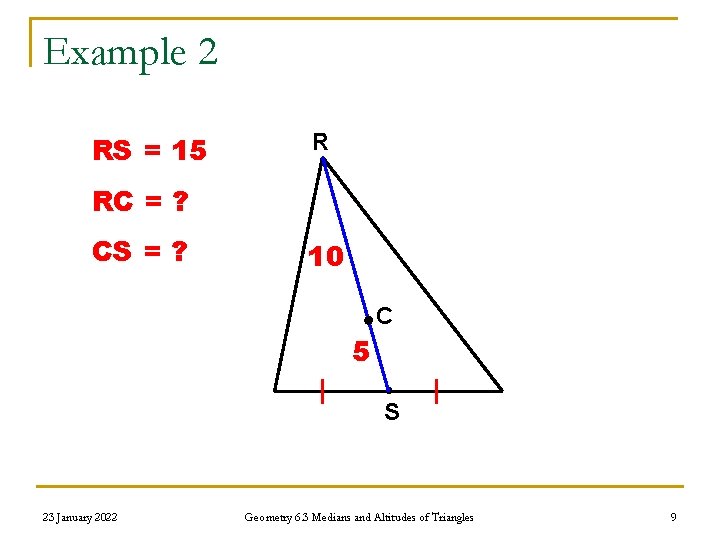
Example 2 RS = 15 R RC = ? CS = ? 10 C 5 S 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 9

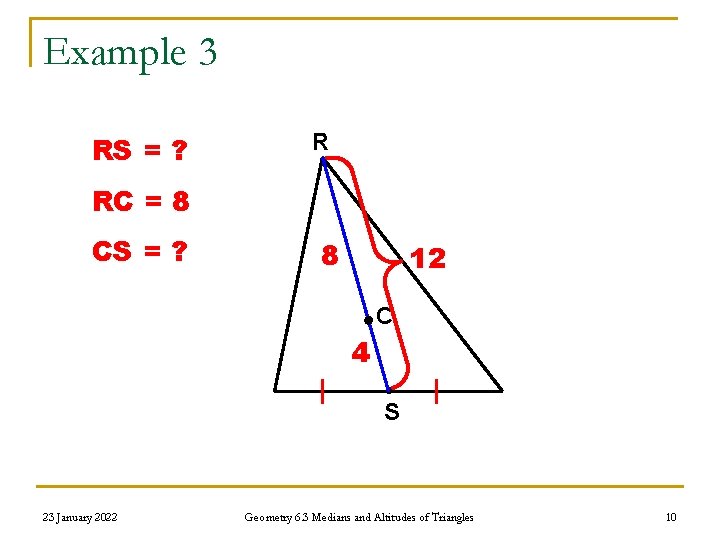
Example 3 RS = ? R RC = 8 CS = ? 8 12 C 4 S 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 10

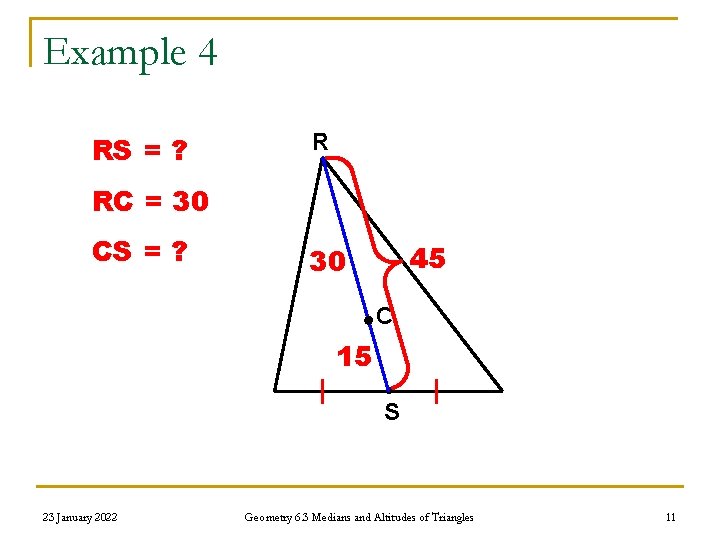
Example 4 RS = ? R RC = 30 CS = ? 45 30 C 15 S 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 11

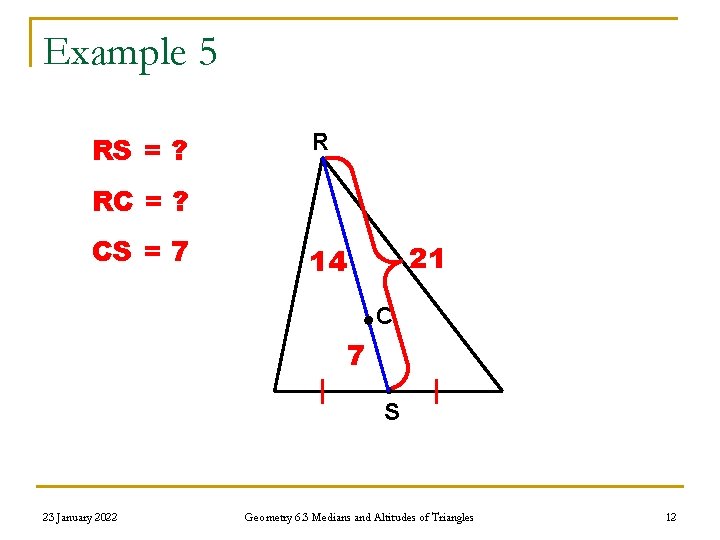
Example 5 RS = ? R RC = ? CS = 7 21 14 C 7 S 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 12

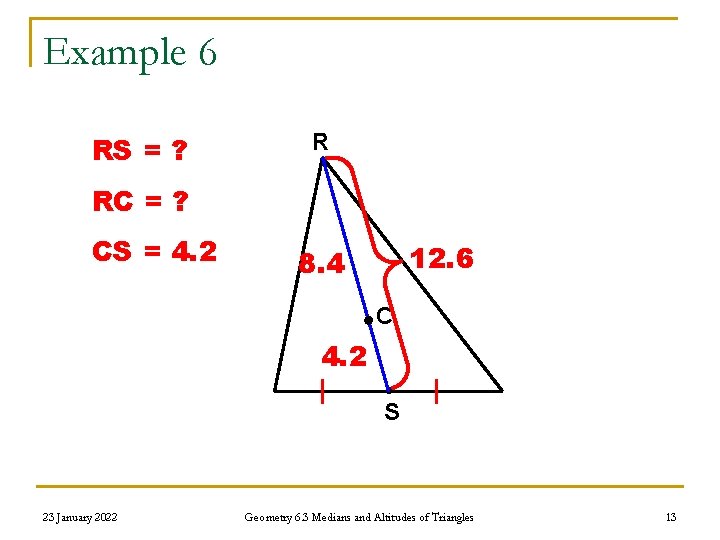
Example 6 RS = ? R RC = ? CS = 4. 2 12. 6 8. 4 C 4. 2 S 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 13

Centroid Property n The centroid of a triangle is also known as the center of balance. 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 14

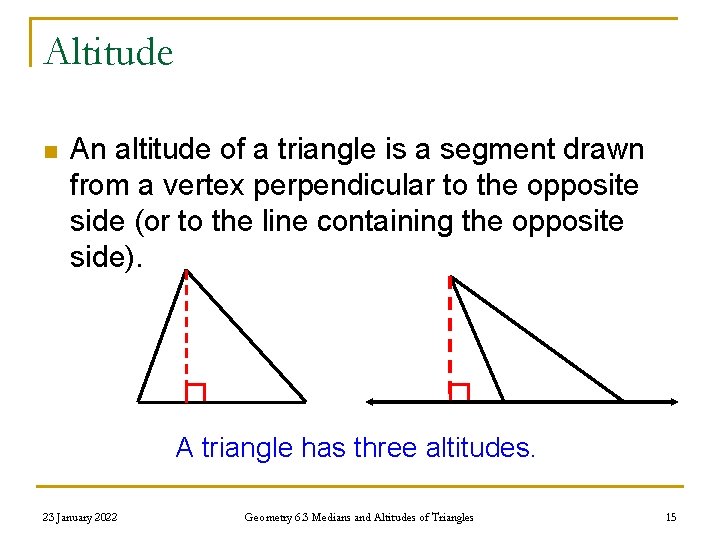
Altitude n An altitude of a triangle is a segment drawn from a vertex perpendicular to the opposite side (or to the line containing the opposite side). A triangle has three altitudes. 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 15

Altitudes n n n The altitudes of a triangle are concurrent. The point of concurrency is called the orthocenter. The orthocenter may be in the triangle’s interior or exterior, or on the triangle. 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 16

Concurrency Summary n n n A median is a segment from a vertex to the midpoint of the opposite side of a triangle. The medians of a triangle are concurrent at the centroid. The centroid divides the median into a ratio of 2: 1. The centroid is the center of balance. An altitude is a segment from a vertex perpendicular to the opposite side. The altitudes are concurrent at the orthocenter. 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 17

Concurrent Points in Triangles n The perpendicular bisectors of the sides are concurrent at the ? q n The angle bisectors of a triangle are concurrent at the? q n Incenter The medians of a triangle are concurrent at the? q n Circumcenter Centroid The altitudes of a triangle are concurrent at the? q Orthocenter 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 18

Fast answers! n n n n The altitudes are concurrent at the ? Orthocenter The medians are concurrent at the ? Centroid The perpendicular bisectors are concurrent at the ? Circumcenter The angle bisectors are concurrent at the ? Incenter 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 19

Fast answers! n n n Which point is equidistant from the sides of a triangle? Incenter Which point is the center of balance? Centroid Which point is equidistant from the vertices? Circumcenter? 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 20

Fast answers! n n n What point is needed to draw a circumcircle? Circumcenter What point is needed to draw an incircle? Incenter What point is needed to find the center of balance? Centroid 23 January 2022 Geometry 6. 3 Medians and Altitudes of Triangles 21