Geometry 4 5 Dilations EQ What does it

Geometry 4. 5 Dilations EQ: What does it mean to dilate a figure?

Topic/Objective l l Identify Dilations Make drawings using dilations. 25 January 2022 Geometry 4. 5 Dilations 2

Rigid Transformations l l Previously studied. Rotations l l Translations These were isometries: The pre-image and the image were congruent. 25 January 2022 Geometry 4. 5 Dilations 3

Dilation l l Dilations are non-rigid transformations. The pre-image and image are similar, but not congruent. 25 January 2022 Geometry 4. 5 Dilations 4

25 January 2022 Geometry 4. 5 Dilations 5

Dilation E n la 25 January 2022 rgemen t Geometry 4. 5 Dilations 6

Dilation Reduction 25 January 2022 Geometry 4. 5 Dilations 7

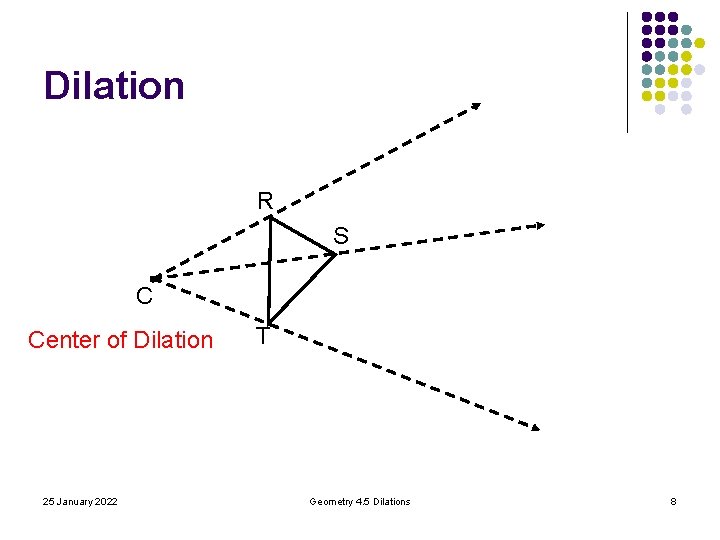
Dilation R S C Center of Dilation 25 January 2022 T Geometry 4. 5 Dilations 8

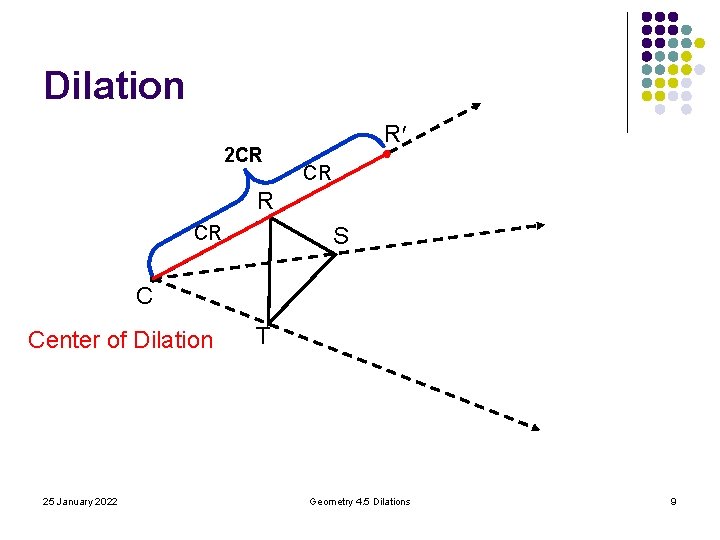
Dilation 2 CR R S CR C Center of Dilation 25 January 2022 T Geometry 4. 5 Dilations 9

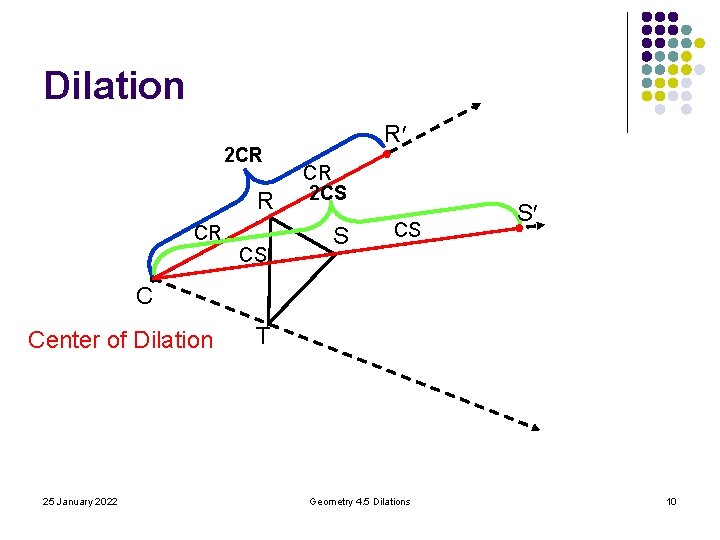
Dilation 2 CR R CR CS R CR 2 CS S C Center of Dilation 25 January 2022 T Geometry 4. 5 Dilations 10

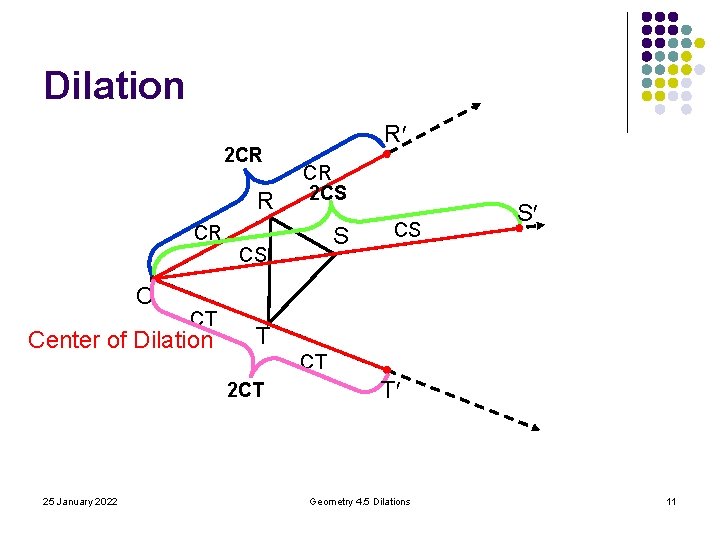
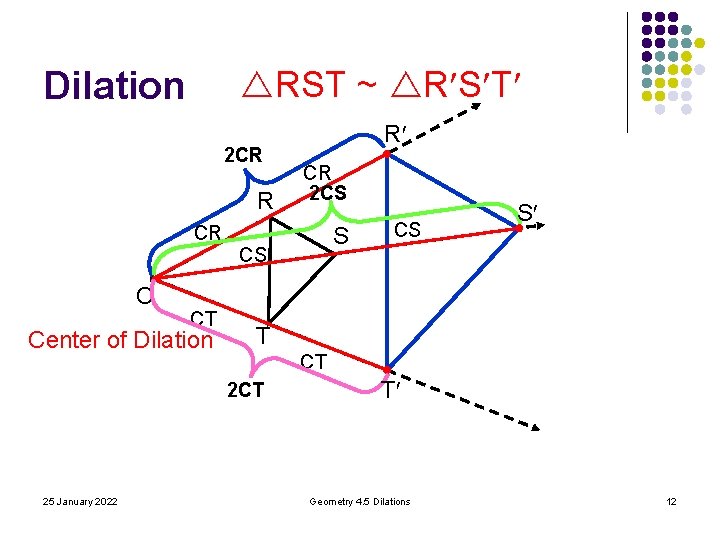
Dilation 2 CR R CR C CT Center of Dilation CR 2 CS S CS CS S T CT 25 January 2022 R T Geometry 4. 5 Dilations 11

RST ~ R S T Dilation 2 CR R CR C CT Center of Dilation CR 2 CS S CS CS S T CT 25 January 2022 R T Geometry 4. 5 Dilations 12

Dilation Definition A dilation with center C and scale factor k is a transformation that maps every point P to a point P’ so that the following properties are true: 1. If P is not the center point C, then the image point P’ lies on CP. The scale factor k is a positive number such that k 1 and 2. If P is the center point C, then P = P’. 3. The dilation is a reduction if 0 < k < 1, and an enlargement if k > 1. 25 January 2022 Geometry 4. 5 Dilations 13

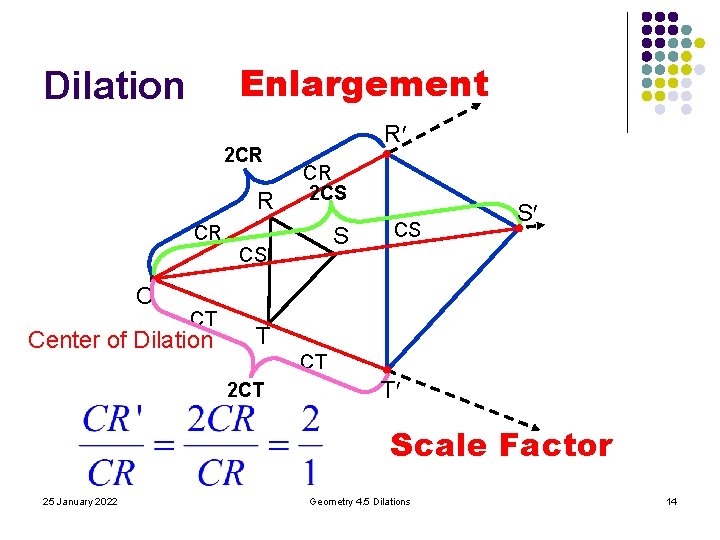
Enlargement Dilation 2 CR R CR C CT Center of Dilation R CR 2 CS S CS CS S T CT 2 CT T Scale Factor 25 January 2022 Geometry 4. 5 Dilations 14

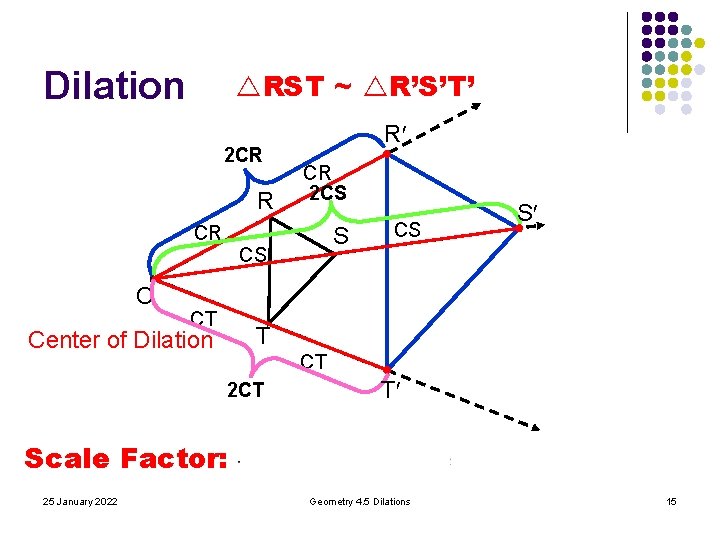
Dilation RST ~ R’S’T’ 2 CR R CR C R CR 2 CS S CS CT CS S T Center of Dilation CT 2 CT T Scale Factor: 25 January 2022 Geometry 4. 5 Dilations 15

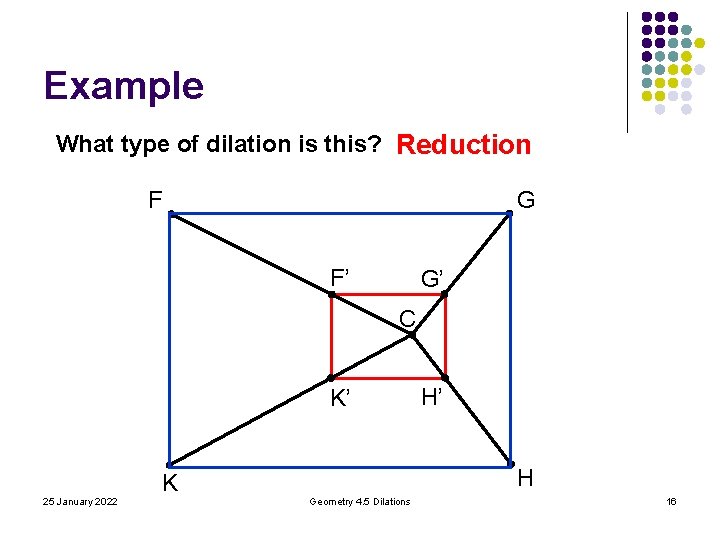
Example What type of dilation is this? Reduction G F F’ G’ C K’ H K 25 January 2022 H’ Geometry 4. 5 Dilations 16

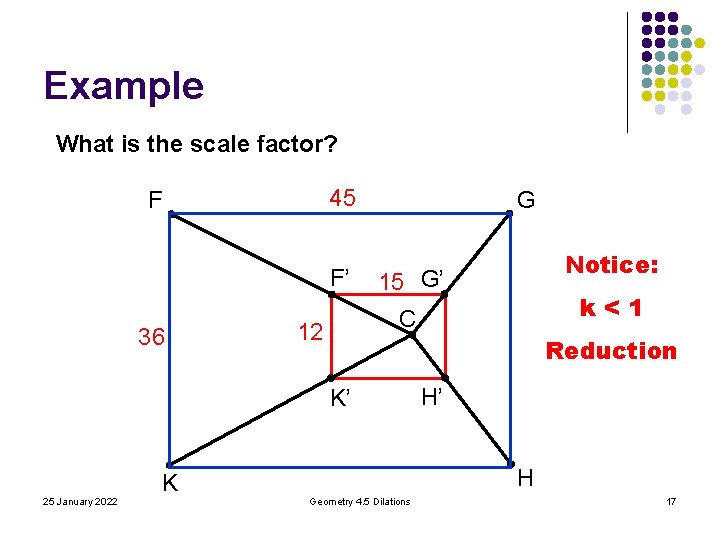
Example What is the scale factor? 45 F F’ 36 G k<1 C 12 Reduction K’ H’ H K 25 January 2022 Notice: 15 G’ Geometry 4. 5 Dilations 17

Remember: l The scale factor k is image segment pre-image segment l l If 0 < k < 1 it’s a reduction. If k > 1 it’s an enlargement. 25 January 2022 Geometry 4. 5 Dilations 18

Coordinate Geometry l l Use the origin (0, 0) as the center of dilation. The image of P(x, y) is P’(kx, ky). Notation: P(x, y) P’(kx, ky). Read: “P maps to P prime” 25 January 2022 Geometry 4. 5 Dilations 19

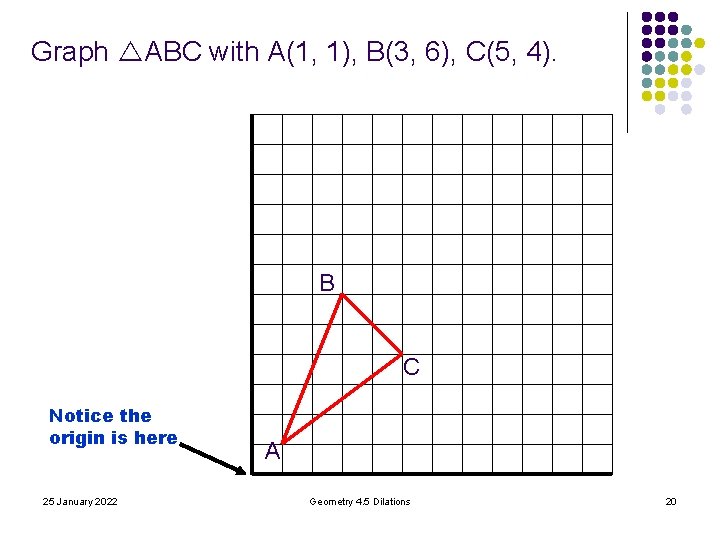
Graph ABC with A(1, 1), B(3, 6), C(5, 4). B C Notice the origin is here 25 January 2022 A Geometry 4. 5 Dilations 20

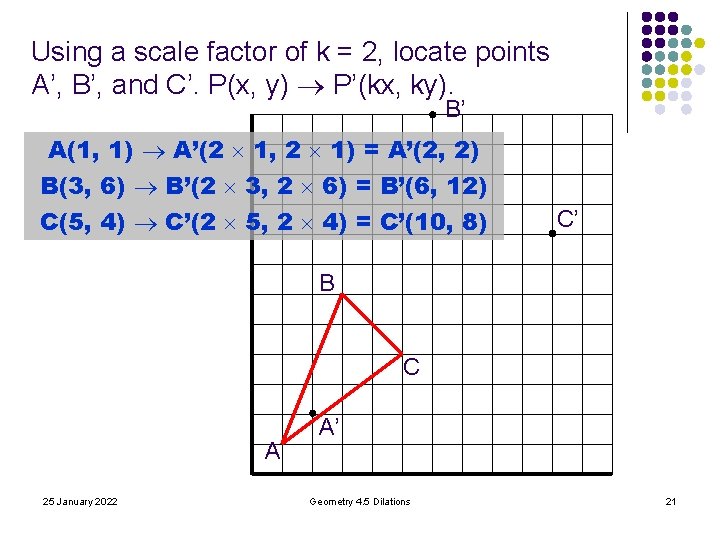
Using a scale factor of k = 2, locate points A’, B’, and C’. P(x, y) P’(kx, ky). B’ A(1, 1) A’(2 1, 2 1) = A’(2, 2) B(3, 6) B’(2 3, 2 6) = B’(6, 12) C(5, 4) C’(2 5, 2 4) = C’(10, 8) C’ B C A 25 January 2022 A’ Geometry 4. 5 Dilations 21

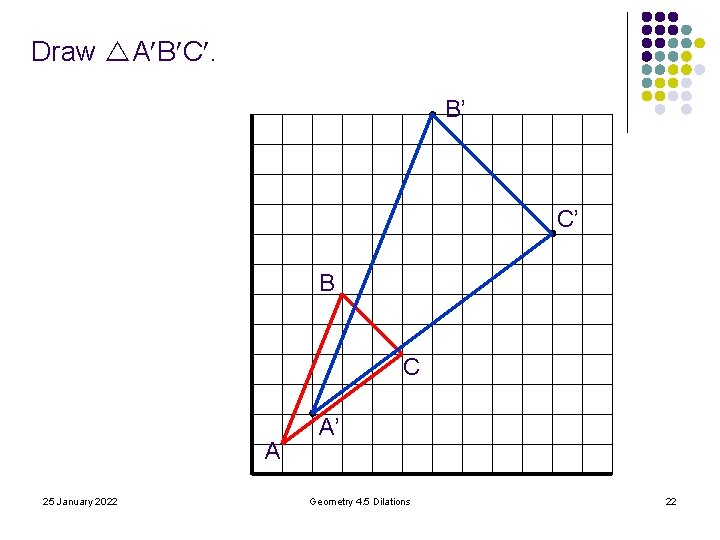
Draw A B C. B’ C’ B C A 25 January 2022 A’ Geometry 4. 5 Dilations 22

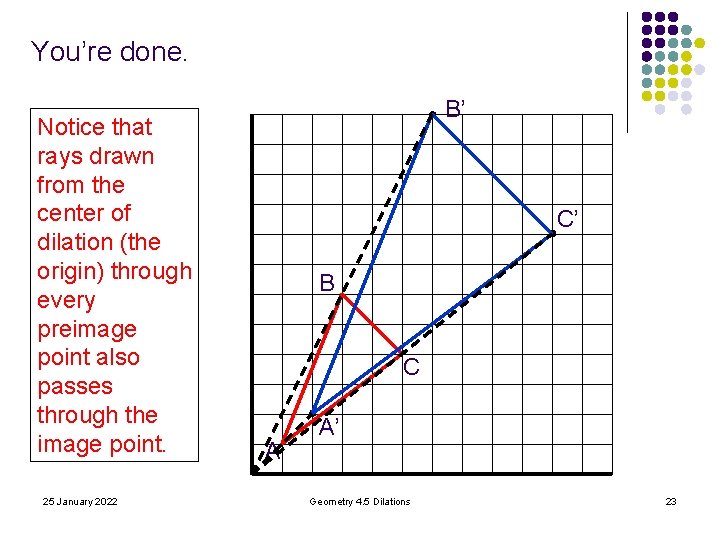
You’re done. Notice that rays drawn from the center of dilation (the origin) through every preimage point also passes through the image point. 25 January 2022 B’ C’ B C A A’ Geometry 4. 5 Dilations 23

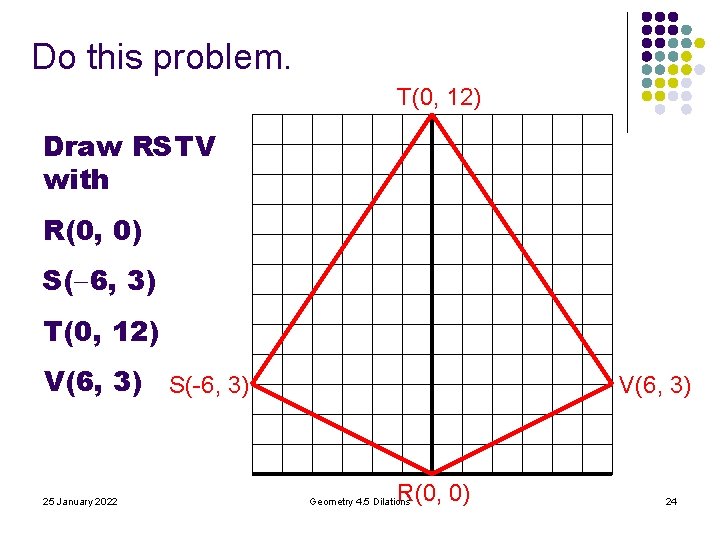
Do this problem. T(0, 12) Draw RSTV with R(0, 0) S( 6, 3) T(0, 12) V(6, 3) S(-6, 3) 25 January 2022 V(6, 3) R(0, 0) Geometry 4. 5 Dilations 24

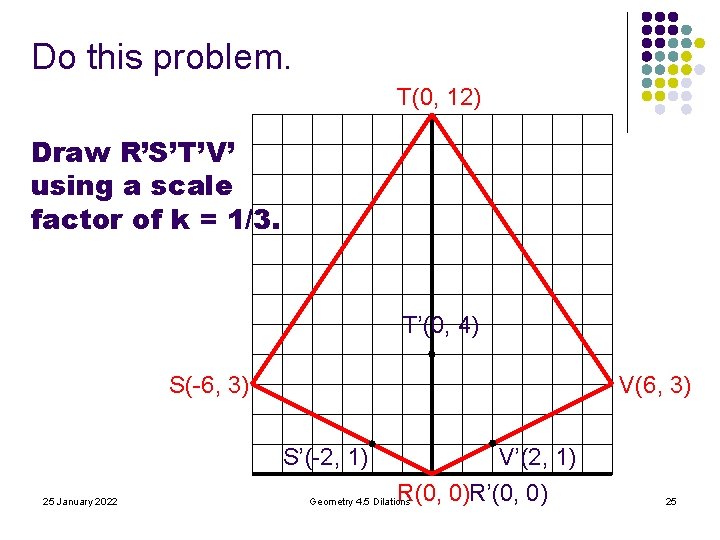
Do this problem. T(0, 12) Draw R’S’T’V’ using a scale factor of k = 1/3. T’(0, 4) S(-6, 3) V(6, 3) S’(-2, 1) 25 January 2022 V’(2, 1) R(0, 0)R’(0, 0) Geometry 4. 5 Dilations 25

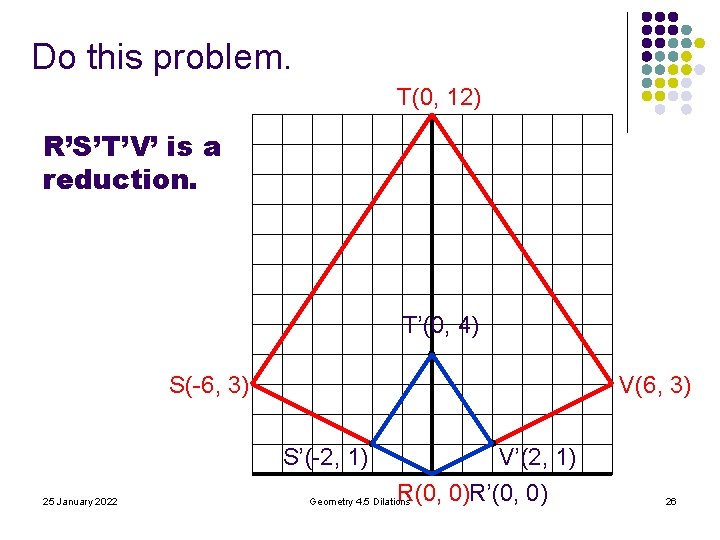
Do this problem. T(0, 12) R’S’T’V’ is a reduction. T’(0, 4) S(-6, 3) V(6, 3) S’(-2, 1) 25 January 2022 V’(2, 1) R(0, 0)R’(0, 0) Geometry 4. 5 Dilations 26

Summary l l l A dilation creates similar figures. A dilation can be a reduction or an enlargement. If the scale factor is less than one, it’s a reduction, and if the scale factor is greater than one it’s an enlargement. 25 January 2022 Geometry 4. 5 Dilations 27

One more time… Image Size Scale Factor = Pre-image Size After Scale Factor = Before 25 January 2022 Geometry 4. 5 Dilations 28

Enlargement or Reduction? l l l CP = 10 and CP’ = 20 Enlargement What is the Scale Factor? 2 k = CP’/CP = 20/10 = 2 25 January 2022 Geometry 4. 5 Dilations 29

Enlargement or Reduction? l l l CP = 150 and CP’ = 15 Reduction What is the Scale Factor? 1/10 k = CP’/CP = 15/150 = 1/10 25 January 2022 Geometry 4. 5 Dilations 30

Enlargement or Reduction? l l l CP = 20 and CP’ = 18 Reduction What is the Scale Factor? 9/10 k = CP’/CP = 18/20 = 9/10 25 January 2022 Geometry 4. 5 Dilations 31

Enlargement or Reduction? l l l CP = 15 and CP’ = 18 Enlargement What is the Scale Factor? 6/5 k = CP’/CP = 18/15 = 6/5 25 January 2022 Geometry 4. 5 Dilations 32