Geometry 4 1 Translations and Vectors EQ How














- Slides: 32

Geometry 4. 1 Translations and Vectors EQ: How do you translate a figure on a coordinate plane?

Goals n n Identify and use translations in the plane. Know what a vector is and use them to solve problems. 2/15/2022 4. 1 Translations and Vectors 2

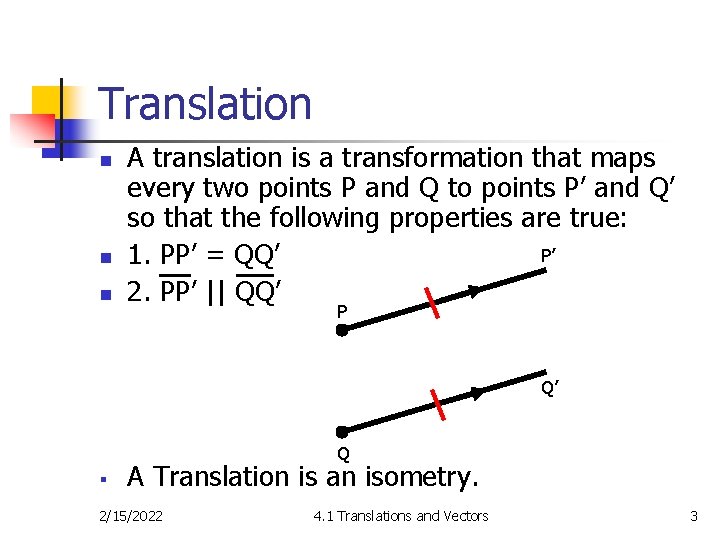
Translation n A translation is a transformation that maps every two points P and Q to points P’ and Q’ so that the following properties are true: P’ 1. PP’ = QQ’ 2. PP’ || QQ’ P Q’ Q § A Translation is an isometry. 2/15/2022 4. 1 Translations and Vectors 3

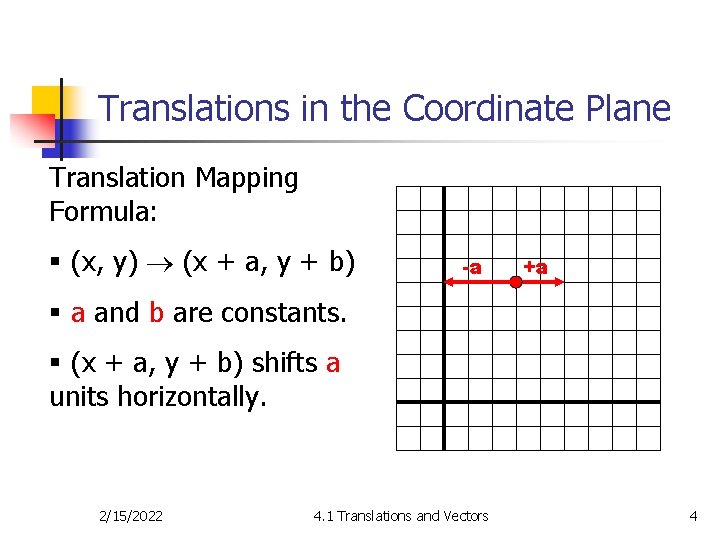
Translations in the Coordinate Plane Translation Mapping Formula: § (x, y) (x + a, y + b) -a +a § a and b are constants. § (x + a, y + b) shifts a units horizontally. 2/15/2022 4. 1 Translations and Vectors 4

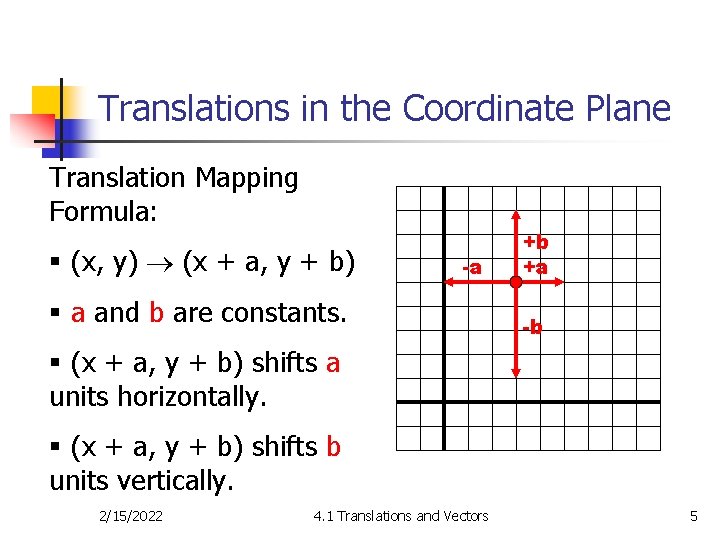
Translations in the Coordinate Plane Translation Mapping Formula: § (x, y) (x + a, y + b) -a § a and b are constants. +b +a -b § (x + a, y + b) shifts a units horizontally. § (x + a, y + b) shifts b units vertically. 2/15/2022 4. 1 Translations and Vectors 5

Use coordinate notation to describe the translation. n n n A point is translated 10 units to the right and 8 units up. (x, y) (x + 10, y + 8) A point is translated 7 units to the left, and 2 units up. (x, y) (x – 7, y + 2) A point is translated 1 unit to the left, and 2 units down. (x, y) (x – 1, y – 2) 2/15/2022 4. 1 Translations and Vectors 6

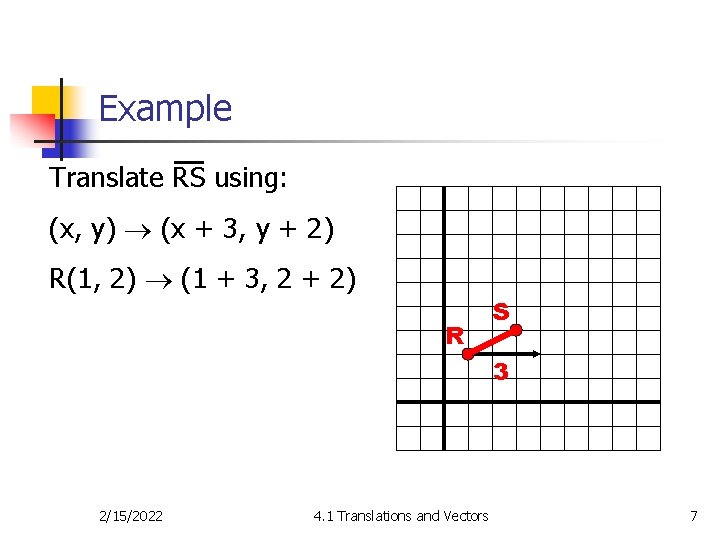
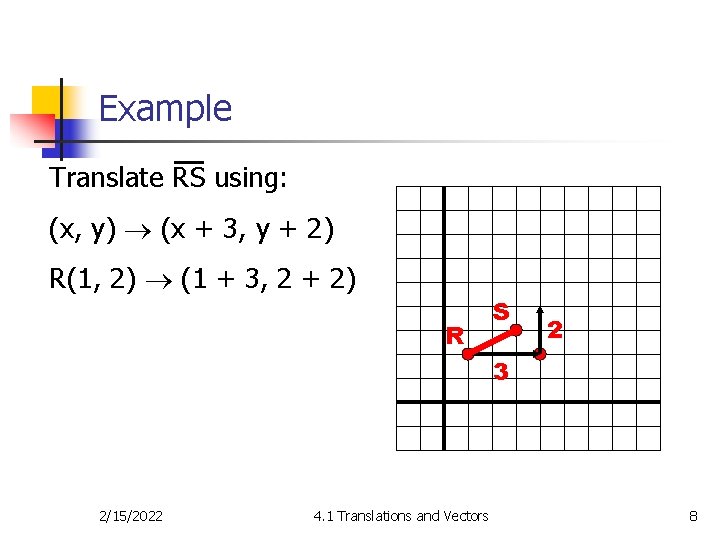
Example Translate RS using: (x, y) (x + 3, y + 2) R(1, 2) (1 + 3, 2 + 2) R S 3 2/15/2022 4. 1 Translations and Vectors 7

Example Translate RS using: (x, y) (x + 3, y + 2) R(1, 2) (1 + 3, 2 + 2) R S 2 3 2/15/2022 4. 1 Translations and Vectors 8

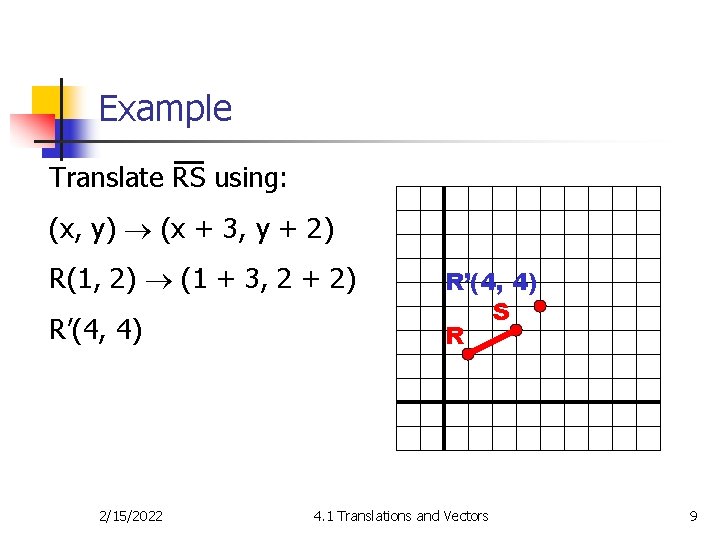
Example Translate RS using: (x, y) (x + 3, y + 2) R(1, 2) (1 + 3, 2 + 2) R’(4, 4) 2/15/2022 R’(4, 4) S R 4. 1 Translations and Vectors 9

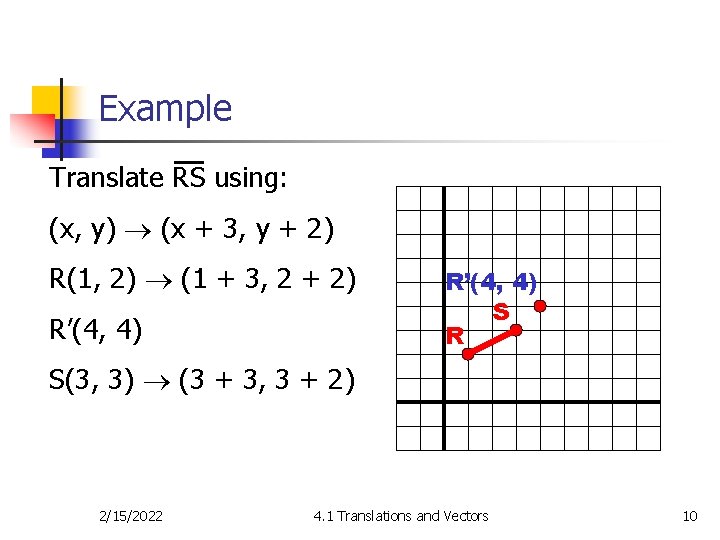
Example Translate RS using: (x, y) (x + 3, y + 2) R(1, 2) (1 + 3, 2 + 2) R’(4, 4) S R S(3, 3) (3 + 3, 3 + 2) 2/15/2022 4. 1 Translations and Vectors 10

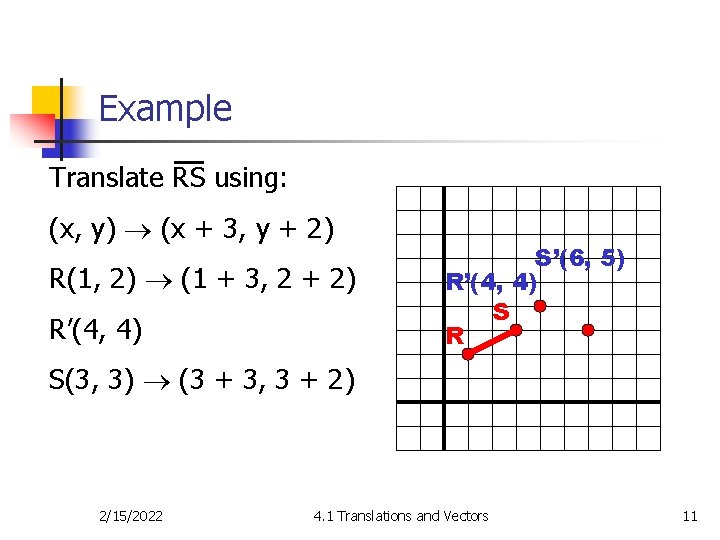
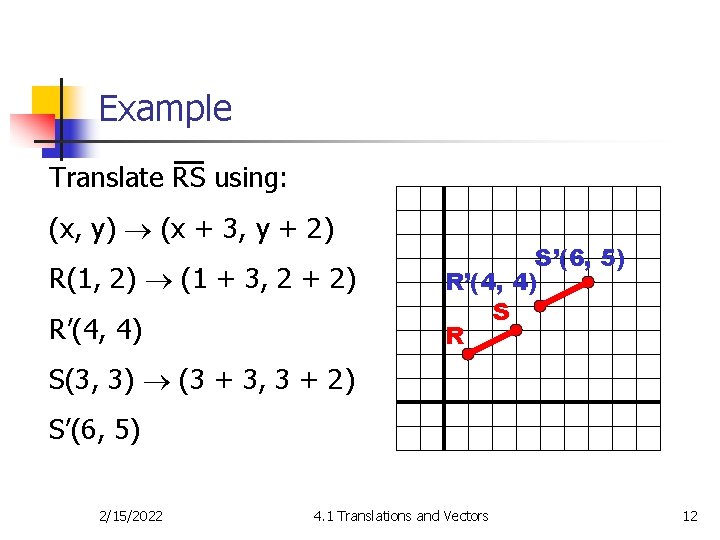
Example Translate RS using: (x, y) (x + 3, y + 2) R(1, 2) (1 + 3, 2 + 2) R’(4, 4) S’(6, 5) R’(4, 4) S R S(3, 3) (3 + 3, 3 + 2) 2/15/2022 4. 1 Translations and Vectors 11

Example Translate RS using: (x, y) (x + 3, y + 2) R(1, 2) (1 + 3, 2 + 2) R’(4, 4) S’(6, 5) R’(4, 4) S R S(3, 3) (3 + 3, 3 + 2) S’(6, 5) 2/15/2022 4. 1 Translations and Vectors 12

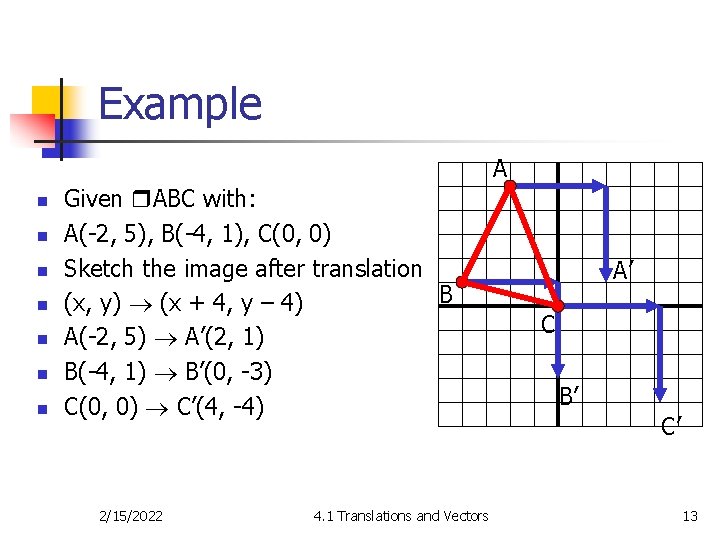
Example A n n n n Given ABC with: A(-2, 5), B(-4, 1), C(0, 0) Sketch the image after translation B (x, y) (x + 4, y – 4) A(-2, 5) A’(2, 1) B(-4, 1) B’(0, -3) C(0, 0) C’(4, -4) 2/15/2022 4. 1 Translations and Vectors A’ C B’ C’ 13

Complete the statement. n n If (4, 0) maps onto (5, 1), then (6, 8) (7, 9) will map onto_______. Why? (4 + 1, 0 + 1) (5, 1) So (6 + 1, 8 + 1) (7, 9) 2/15/2022 4. 1 Translations and Vectors 14

Complete the statement. n n If (7, 8) maps onto (4, 10), then (20, 5) (17, 7) will map onto_______. Why? (7 – 3, 8 + 2) (4, 10) So (20 – 3, 5 + 2) (17, 7) 2/15/2022 4. 1 Translations and Vectors 15

Vectors n n A vector is a quantity that has both direction and magnitude (size). Represented with a arrow drawn between two points. Initial Point A Terminal Point B Vector AB 2/15/2022 4. 1 Translations and Vectors 16

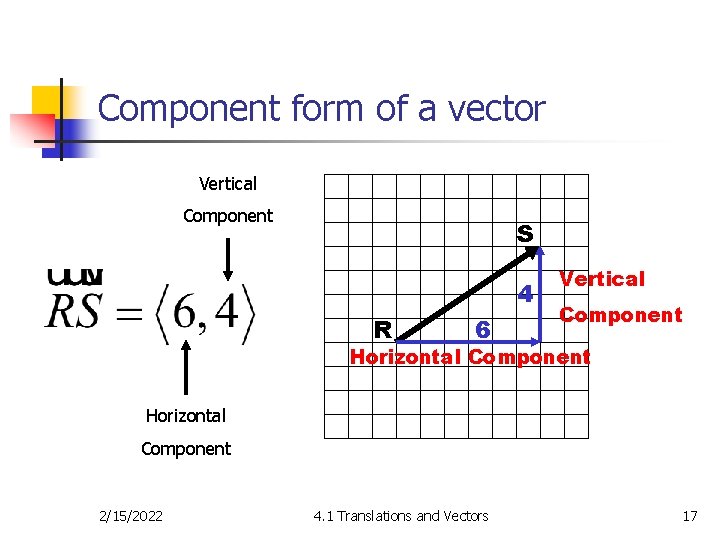
Component form of a vector Vertical Component S 4 R 6 Vertical Component Horizontal Component 2/15/2022 4. 1 Translations and Vectors 17

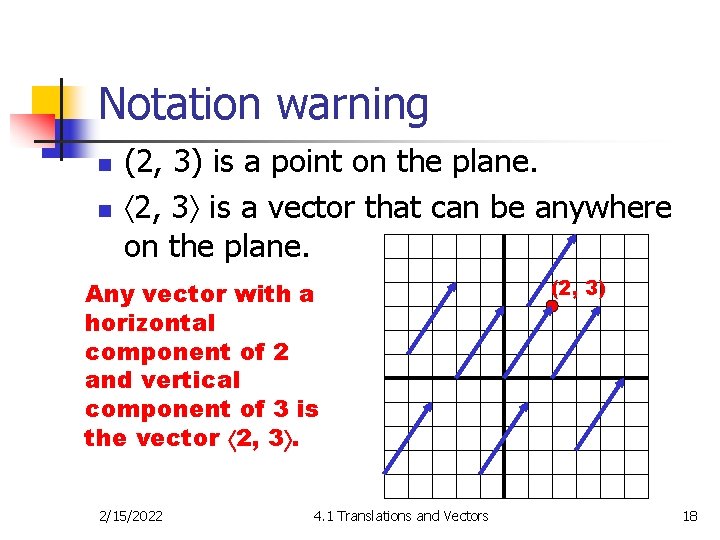
Notation warning n n (2, 3) is a point on the plane. 2, 3 is a vector that can be anywhere on the plane. Any vector with a horizontal component of 2 and vertical component of 3 is the vector 2, 3. 2/15/2022 4. 1 Translations and Vectors (2, 3) 18

Component Form n n n h > 0 shift right 3, … h < 0 shift left -2, … v > 0 shift up …, 9 v < 0 shift down …, -5 h = 0 no horizontal shift 0, … v = 0 no vertical shift …, 0 2/15/2022 4. 1 Translations and Vectors 19

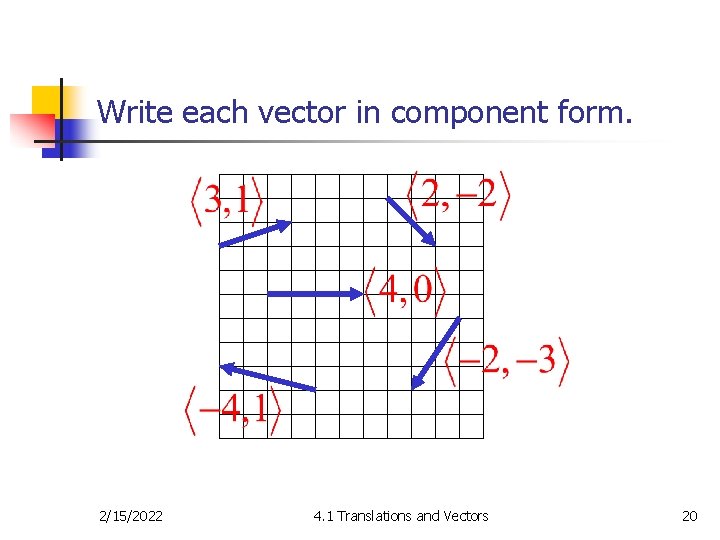
Write each vector in component form. 2/15/2022 4. 1 Translations and Vectors 20

Translation by Vectors n n From each given point, draw the vector a, b. The terminal points is where the translated points are. 2/15/2022 4. 1 Translations and Vectors 21

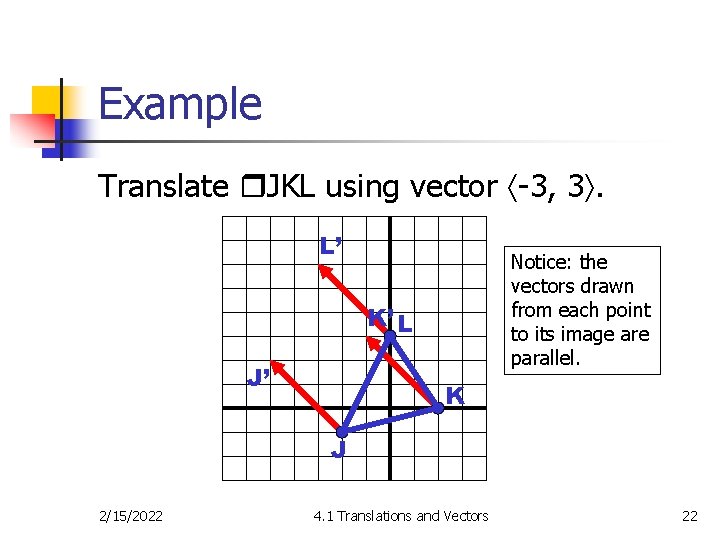
Example Translate JKL using vector -3, 3. L’ Notice: the vectors drawn from each point to its image are parallel. K’ L J’ K J 2/15/2022 4. 1 Translations and Vectors 22

Vector Addition n n Vector u = a, b Vector v = c, d Vector sum: u + v = a, b + c, d = a + c, b + d 2/15/2022 4. 1 Translations and Vectors 23

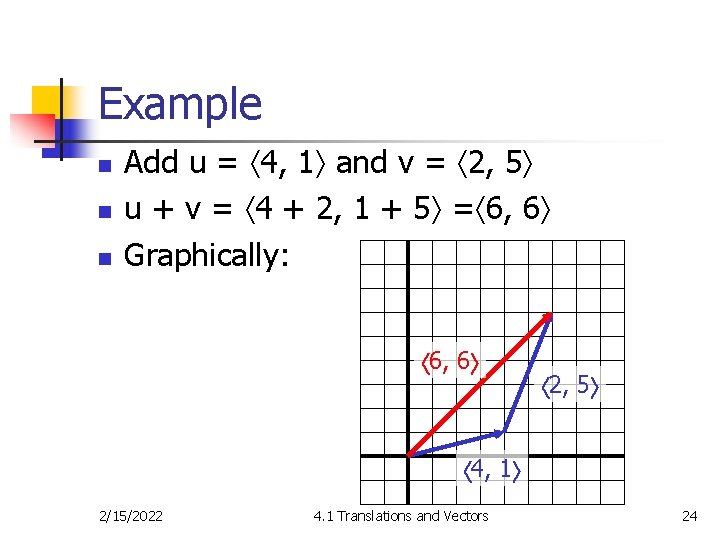
Example n n n Add u = 4, 1 and v = 2, 5 u + v = 4 + 2, 1 + 5 = 6, 6 Graphically: 6, 6 2, 5 4, 1 2/15/2022 4. 1 Translations and Vectors 24

Example n n n u = 1, 2 , v = 3, -6 , w = -6, 1 Find u + v + w and sketch a graph. Solution: 1, 2 + 3, -6 + -6, 1 = 1 + 3 – 6, 2 – 6 + 1 = -2, -3 2/15/2022 4. 1 Translations and Vectors 25

Postulate/Theorem Postulate 4. 1: Translation Postulate A translation is a rigid motion Theorem 4. 1: Composition Theorem The composition of two or more rigid motions is a rigid motion 2/15/2022 4. 1 Translations and Vectors 26

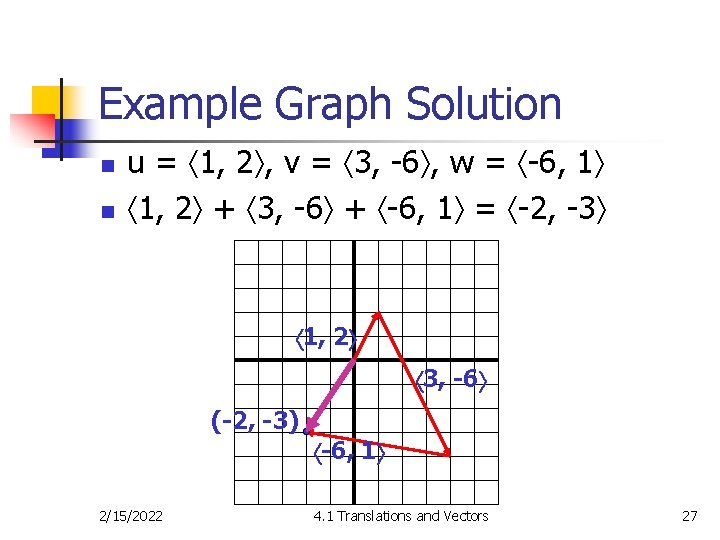
Example Graph Solution n n u = 1, 2 , v = 3, -6 , w = -6, 1 1, 2 + 3, -6 + -6, 1 = -2, -3 1, 2 3, -6 (-2, -3) -6, 1 2/15/2022 4. 1 Translations and Vectors 27

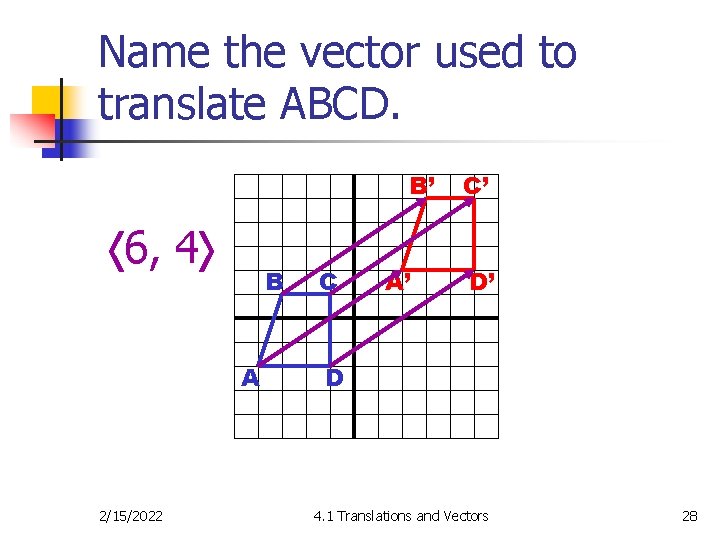
Name the vector used to translate ABCD. B’ 6, 4 B A 2/15/2022 C A’ C’ D’ D 4. 1 Translations and Vectors 28

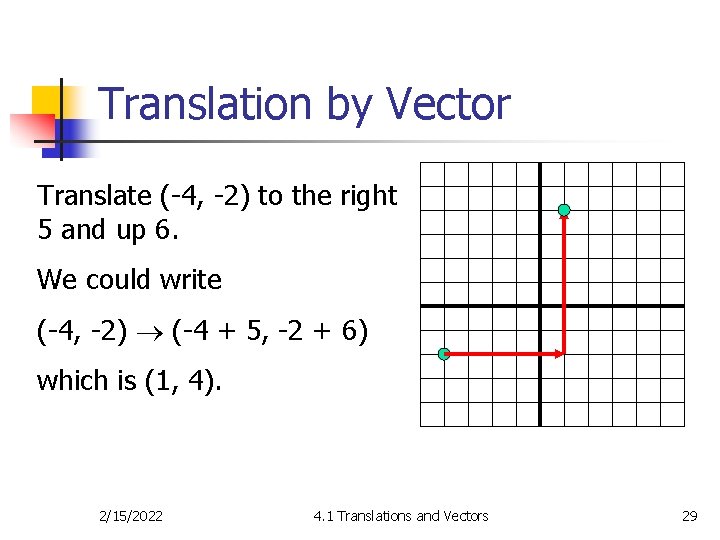
Translation by Vector Translate (-4, -2) to the right 5 and up 6. We could write (-4, -2) (-4 + 5, -2 + 6) which is (1, 4). 2/15/2022 4. 1 Translations and Vectors 29

Translation by Vector What vector translates (-4, -2) to (1, 4)? 5, 6 We could also say: Translate (-4, -2) by 5, 6. (-4, -2) + 5, 6 = (1, 4). 2/15/2022 4. 1 Translations and Vectors 30

Example n n Translate ABC by 4, -3. A(-4, 8) B(-10, -2) C(-22, 15) 2/15/2022 n n A’B’C’ A’(0, 5) B’(-6, -5) C’(-18, 12) 4. 1 Translations and Vectors 31

Summary n n n n A translation shifts a figure horizontally or vertically. A translation is an isometry. Translation formula: (x, y) (x + a, y + b) Translations can be done by vectors. Vectors have direction and magnitude. Vectors are written as h, v. Vector addition: a, b + c, d = a+c, b+d 2/15/2022 4. 1 Translations and Vectors 32