Geometry 2 Index Page 2 Page 14 Page



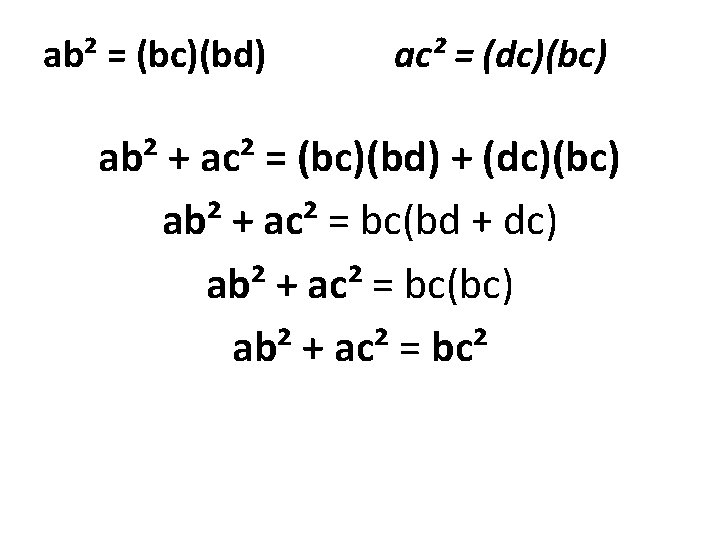
- Slides: 34

Geometry 2 Index Page 2 Page 14 Page 21 Page 24 Angle at centre of circle theorem Example questions from chapter Ratio of two sides of a triangle Similar triangles

The Circle

How can we use this?

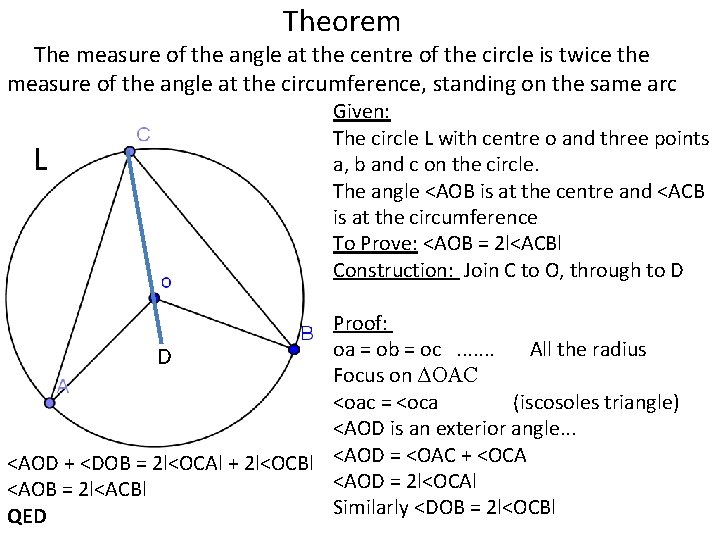
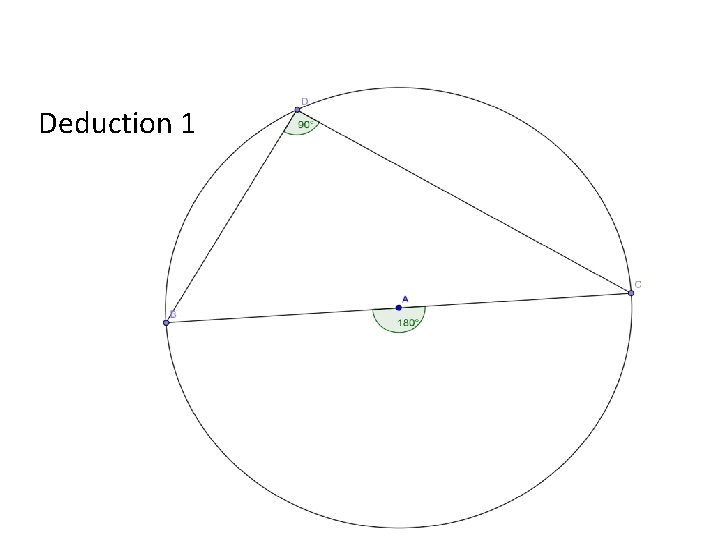
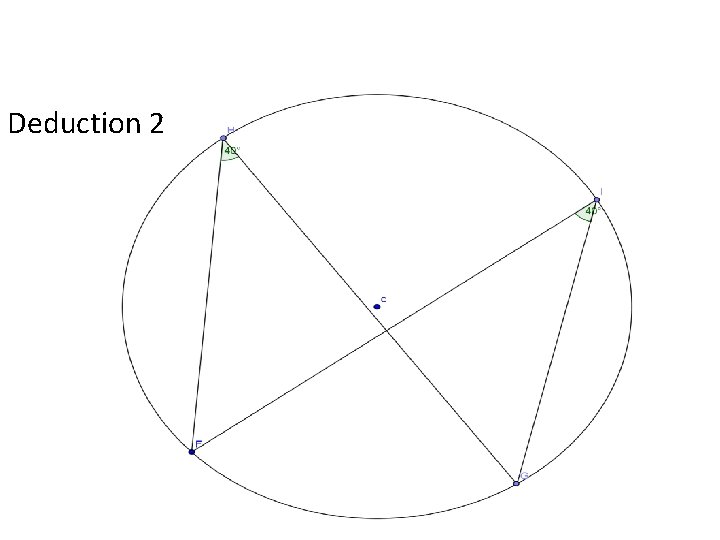
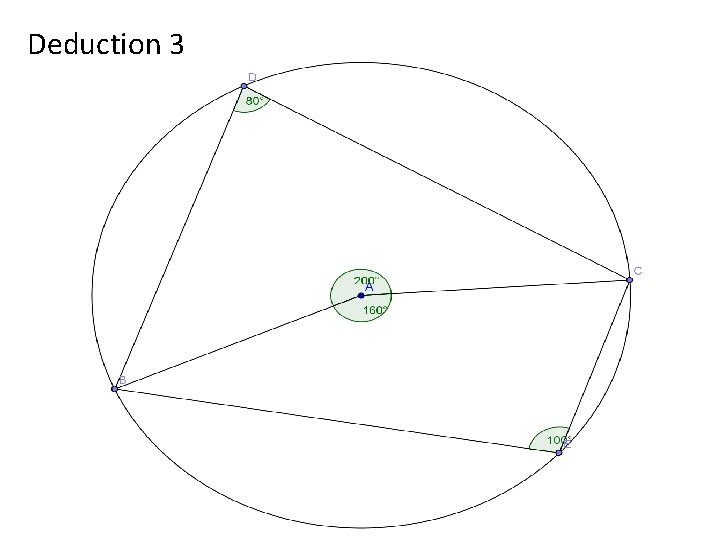
Theorem The measure of the angle at the centre of the circle is twice the measure of the angle at the circumference, standing on the same arc L Given: The circle L with centre o and three points a, b and c on the circle. The angle <AOB is at the centre and <ACB is at the circumference To Prove: <AOB = 2 l<ACBl Construction: Join C to O, through to D Proof: oa = ob = oc. . . . All the radius D Focus on ΔOAC <oac = <oca (iscosoles triangle) <AOD is an exterior angle. . . <AOD + <DOB = 2 l<OCAl + 2 l<OCBl <AOD = <OAC + <OCA <AOD = 2 l<OCAl <AOB = 2 l<ACBl Similarly <DOB = 2 l<OCBl QED

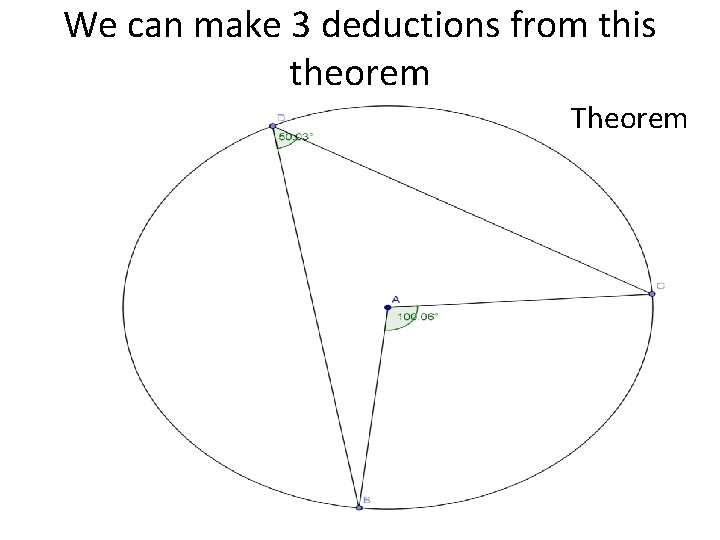
We can make 3 deductions from this theorem Theorem

Deduction 1

Deduction 2

Deduction 3

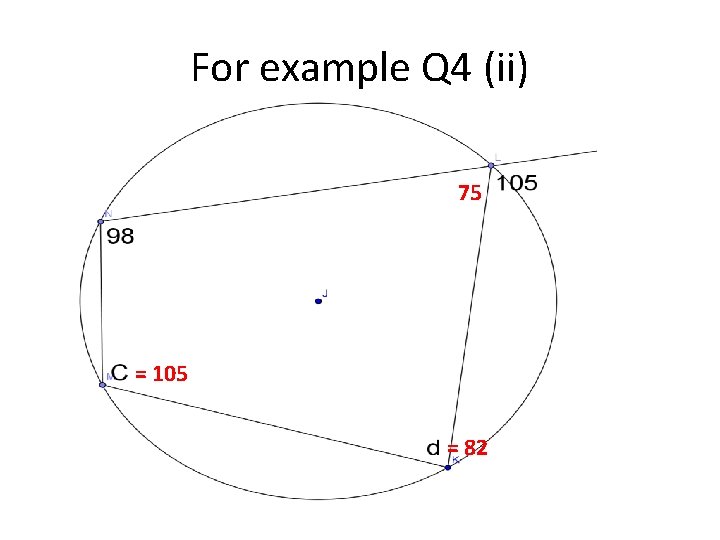
For example Q 4 (ii) 75 = 105 = 82

(iii) Opposite angles in a cyclic quadrilateral add up to 180. . e + 2 e = 180 3 e = 180 e = 69

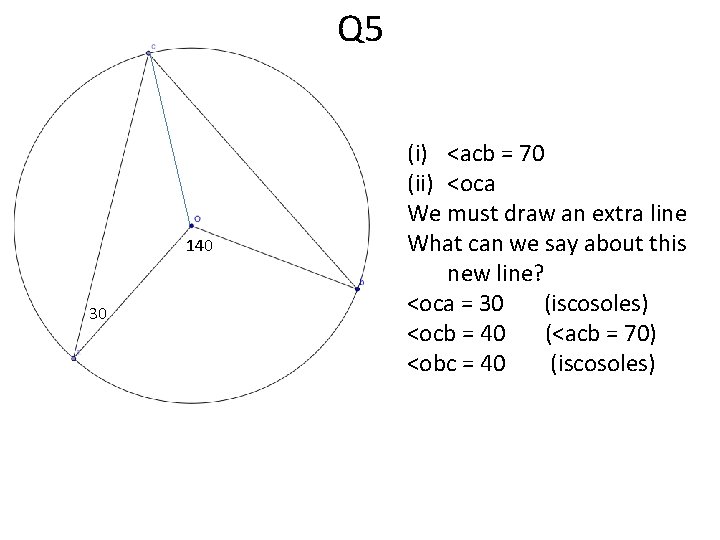
Q 5 140 30 (i) <acb = 70 (ii) <oca We must draw an extra line What can we say about this new line? <oca = 30 (iscosoles) <ocb = 40 (<acb = 70) <obc = 40 (iscosoles)

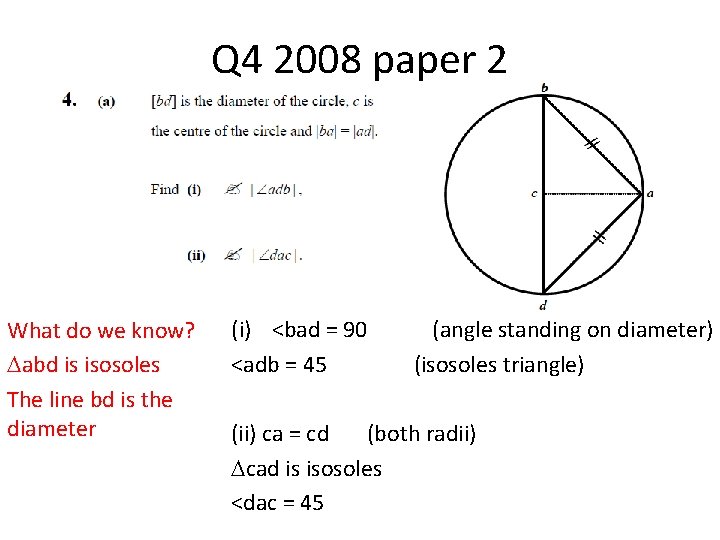
Q 4 2008 paper 2 What do we know? abd is isosoles The line bd is the diameter (i) <bad = 90 <adb = 45 (angle standing on diameter) (isosoles triangle) (ii) ca = cd (both radii) cad is isosoles <dac = 45

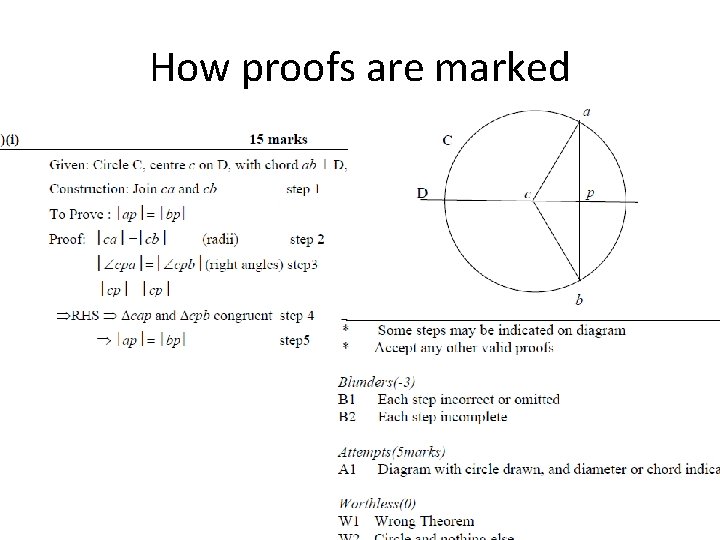
How proofs are marked

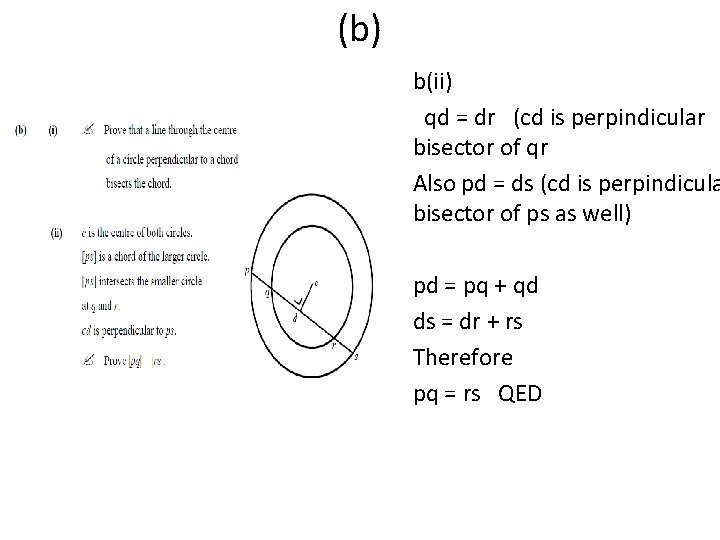
(b) b(ii) qd = dr (cd is perpindicular bisector of qr Also pd = ds (cd is perpindicula bisector of ps as well) pd = pq + qd ds = dr + rs Therefore pq = rs QED

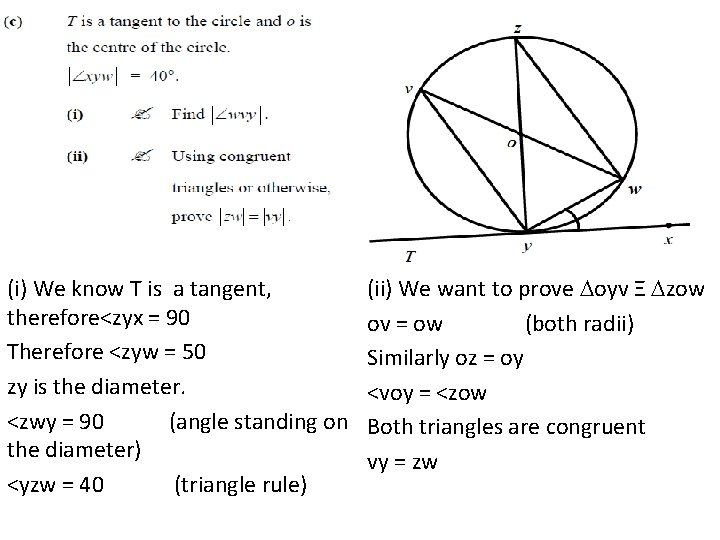
(c) (i) We know T is a tangent, therefore<zyx = 90 Therefore <zyw = 50 zy is the diameter. <zwy = 90 (angle standing on the diameter) <yzw = 40 (triangle rule) (ii) We want to prove oyv Ξ zow ov = ow (both radii) Similarly oz = oy <voy = <zow Both triangles are congruent vy = zw

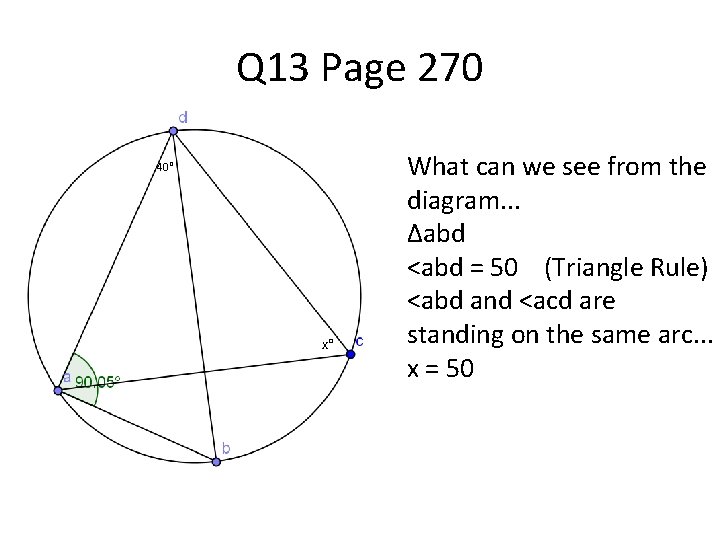
Q 13 Page 270 40° x° What can we see from the diagram. . . ∆abd <abd = 50 (Triangle Rule) <abd and <acd are standing on the same arc. . . x = 50

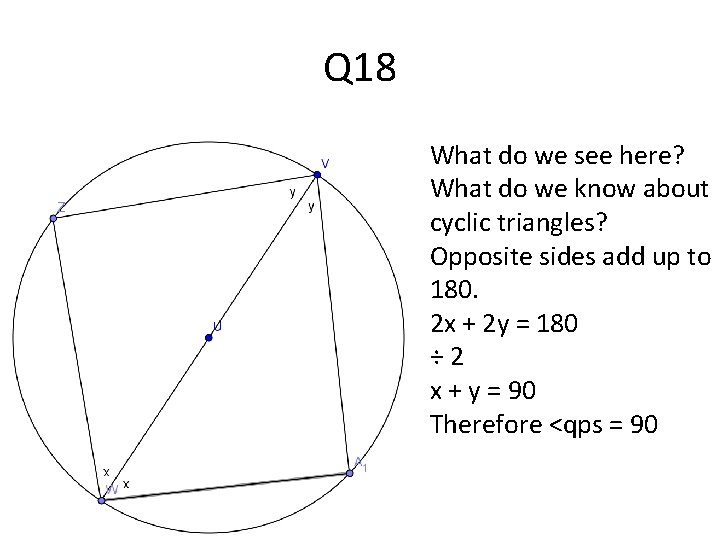
Q 18 What do we see here? What do we know about cyclic triangles? Opposite sides add up to 180. 2 x + 2 y = 180 ÷ 2 x + y = 90 Therefore <qps = 90

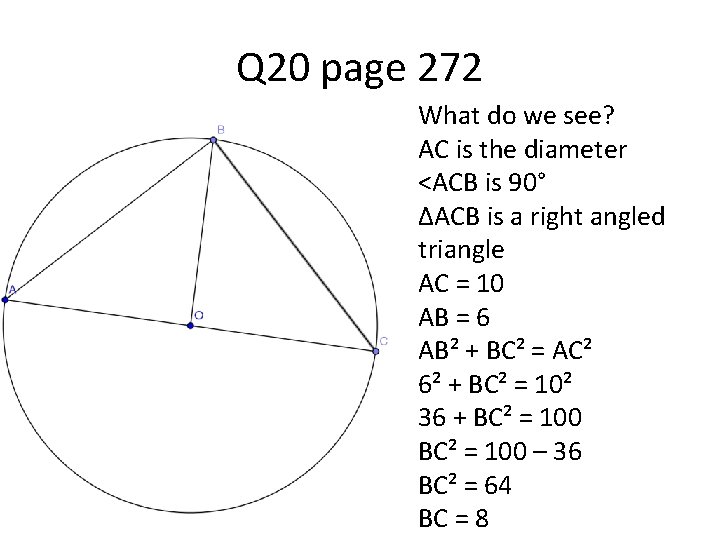
Q 20 page 272 What do we see? AC is the diameter <ACB is 90° ∆ACB is a right angled triangle AC = 10 AB = 6 AB² + BC² = AC² 6² + BC² = 10² 36 + BC² = 100 – 36 BC² = 64 BC = 8

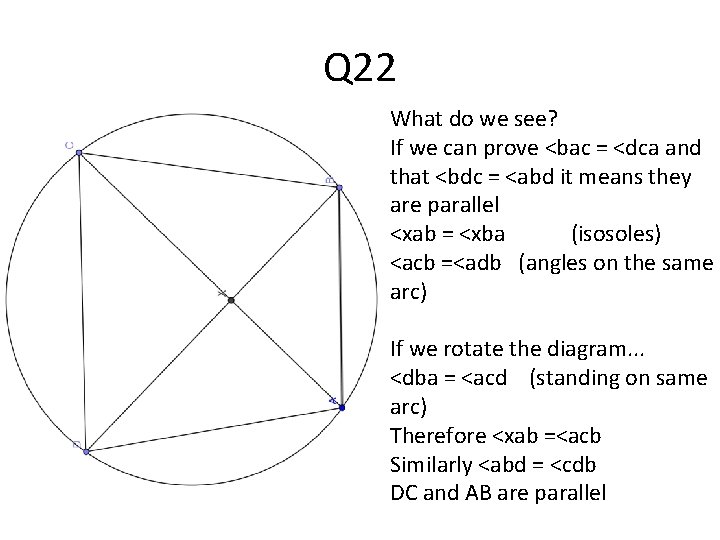
Q 22 What do we see? If we can prove <bac = <dca and that <bdc = <abd it means they are parallel <xab = <xba (isosoles) <acb =<adb (angles on the same arc) If we rotate the diagram. . . <dba = <acd (standing on same arc) Therefore <xab =<acb Similarly <abd = <cdb DC and AB are parallel

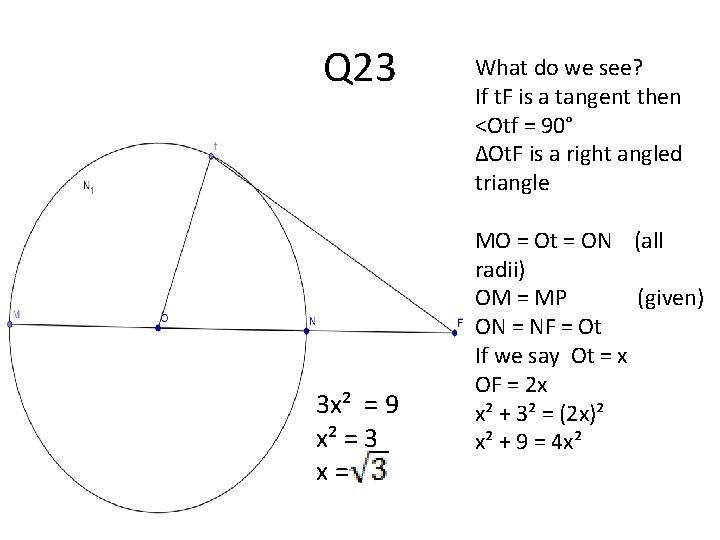
Q 23 3 x² = 9 x² = 3 x= What do we see? If t. F is a tangent then <Otf = 90° ∆Ot. F is a right angled triangle MO = Ot = ON (all radii) OM = MP (given) ON = NF = Ot If we say Ot = x OF = 2 x x² + 3² = (2 x)² x² + 9 = 4 x²

Ratio of sides of angles 4 cm Here we have a triangle that is cut in two by a line parallel to the base. Rule: The parallel line cuts both sides (DC and GE) in the same ratio. 12 cm Uses: If we know the side CD is 12 cm then how long is CG and GE? CD is cut in the ratio 4 : 2 so therefore CE must be cut in the same ratio If we divide 12 in a ratio of 4 : 2 we will get 8 : 4 Therefore CG = 8 cm and GE = 4 cm

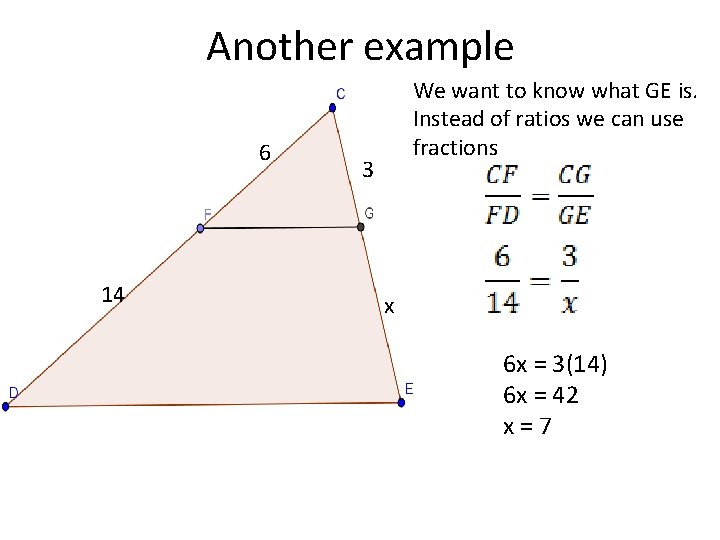
Another example 6 14 We want to know what GE is. Instead of ratios we can use fractions 3 x 6 x = 3(14) 6 x = 42 x=7

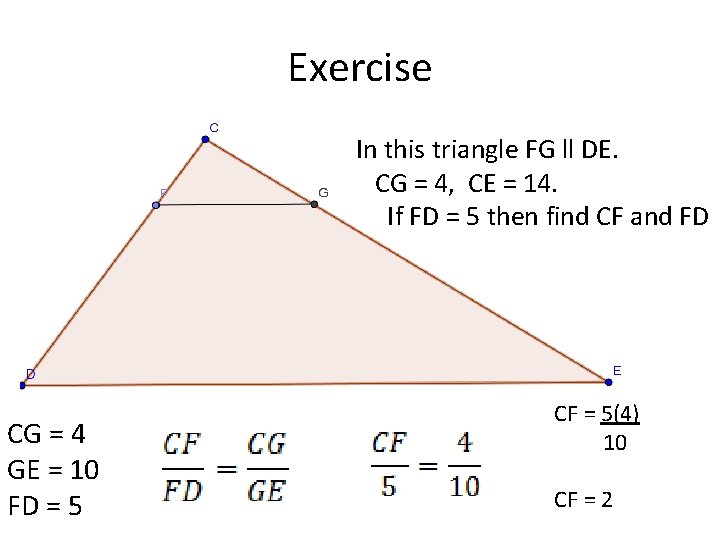
Exercise In this triangle FG ll DE. CG = 4, CE = 14. If FD = 5 then find CF and FD CG = 4 GE = 10 FD = 5 CF = 5(4) 10 CF = 2

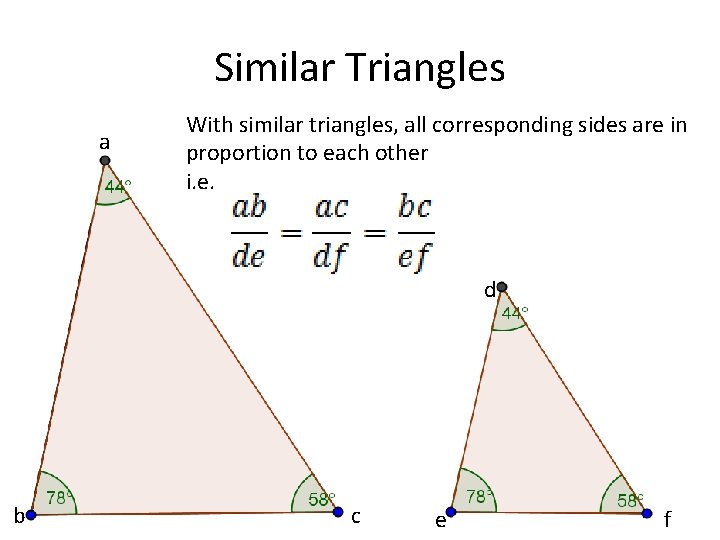
Similar Triangles a With similar triangles, all corresponding sides are in proportion to each other i. e. d b c e f

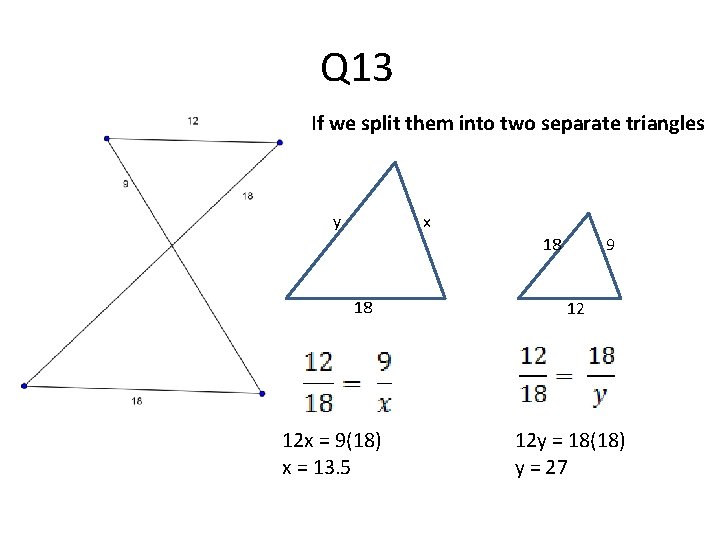
Q 13 If we split them into two separate triangles y x 18 18 12 x = 9(18) x = 13. 5 9 12 12 y = 18(18) y = 27

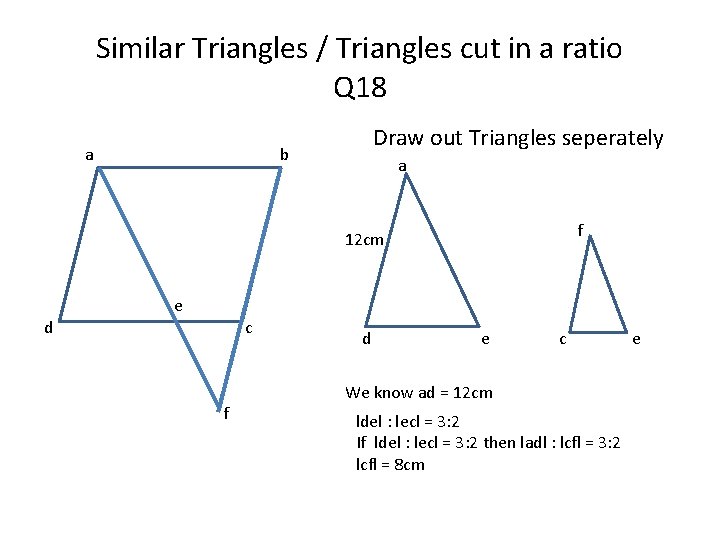
Similar Triangles / Triangles cut in a ratio Q 18 a Draw out Triangles seperately b a f 12 cm d e c f d e c We know ad = 12 cm ldel : lecl = 3: 2 If ldel : lecl = 3: 2 then ladl : lcfl = 3: 2 lcfl = 8 cm e

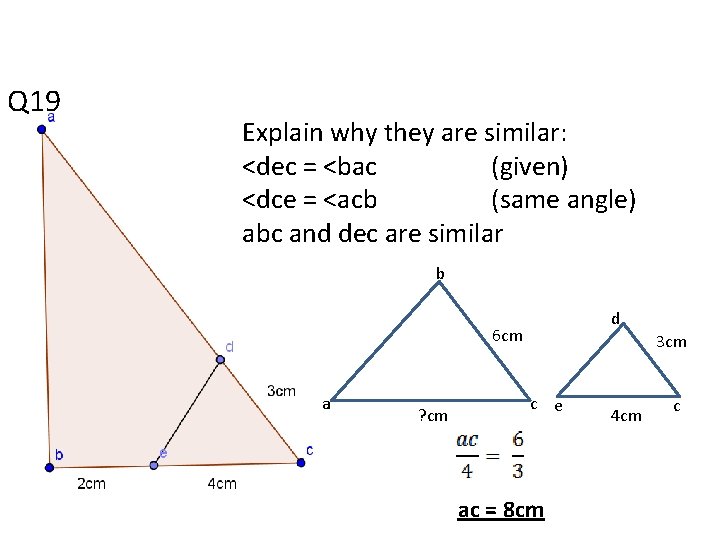
Q 19 Explain why they are similar: <dec = <bac (given) <dce = <acb (same angle) abc and dec are similar b d 6 cm a ? cm 3 cm c e ac = 8 cm 4 cm c

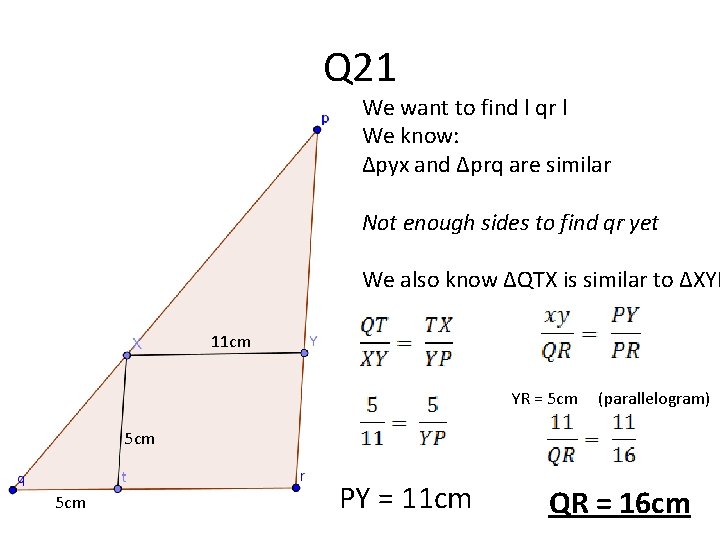
Q 21 We want to find l qr l We know: ∆pyx and ∆prq are similar Not enough sides to find qr yet We also know ∆QTX is similar to ∆XYP 11 cm YR = 5 cm (parallelogram) 5 cm PY = 11 cm QR = 16 cm

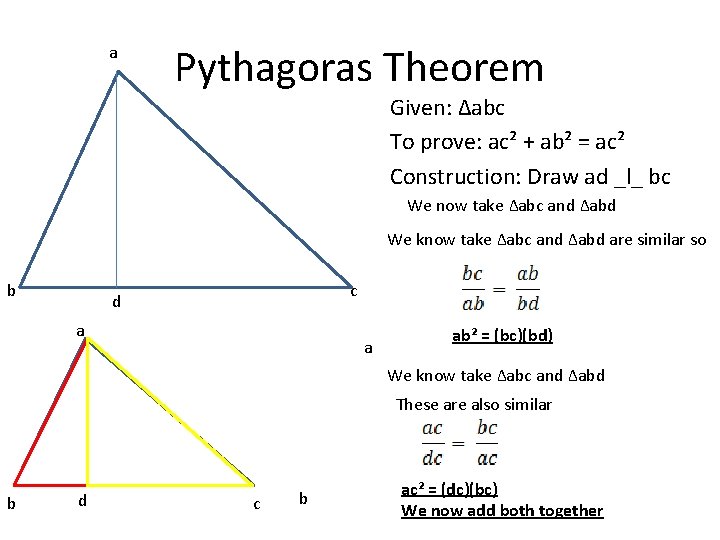
a Pythagoras Theorem Given: ∆abc To prove: ac² + ab² = ac² Construction: Draw ad _l_ bc We now take ∆abc and ∆abd We know take ∆abc and ∆abd are similar so b c d a a ab² = (bc)(bd) We know take ∆abc and ∆abd These are also similar b d c b ac² = (dc)(bc) We now add both together
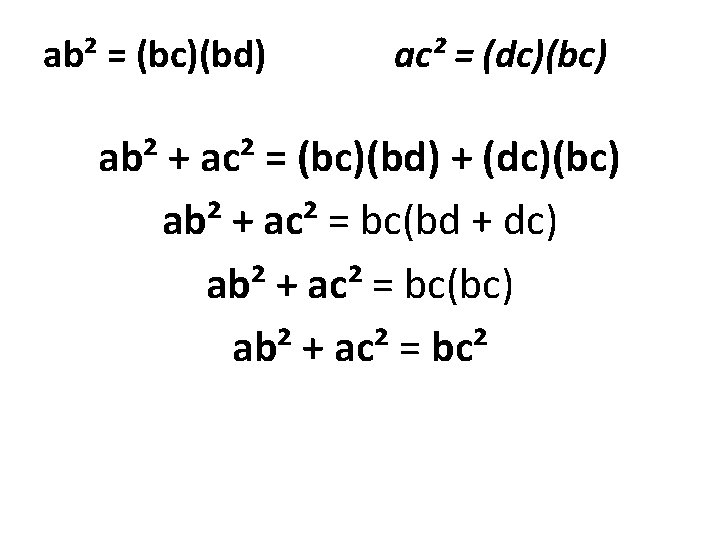
ab² = (bc)(bd) ac² = (dc)(bc) ab² + ac² = (bc)(bd) + (dc)(bc) ab² + ac² = bc(bd + dc) ab² + ac² = bc(bc) ab² + ac² = bc²

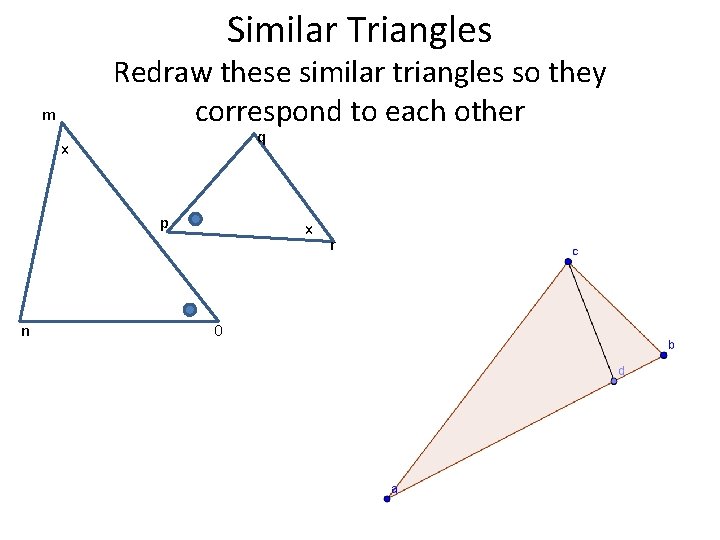
Similar Triangles Redraw these similar triangles so they correspond to each other m q x p n x 0 r

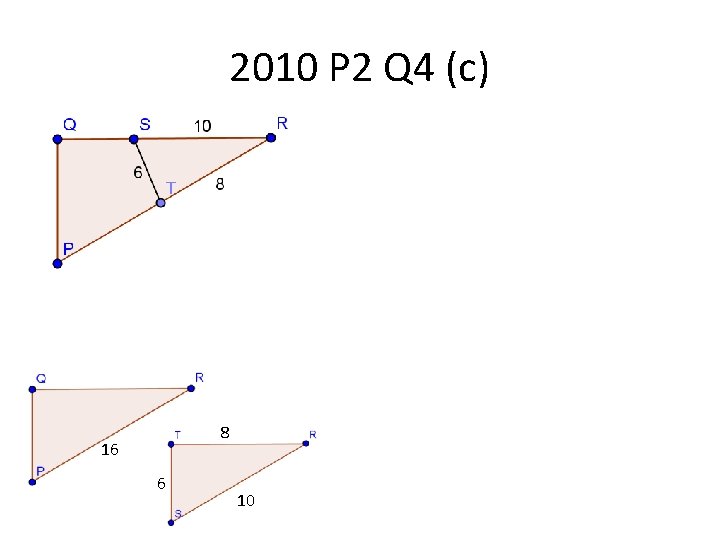
2010 P 2 Q 4 (c) 8 16 6 10

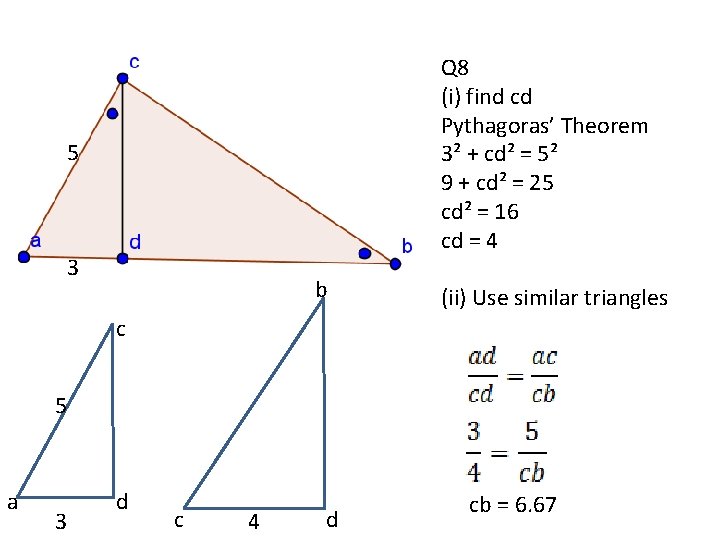
Q 8 5 3 b Q 8 (i) find cd Pythagoras’ Theorem 3² + cd² = 5² 9 + cd² = 25 cd² = 16 cd = 4 (ii) Use similar triangles c 5 a 3 d c 4 d cb = 6. 67

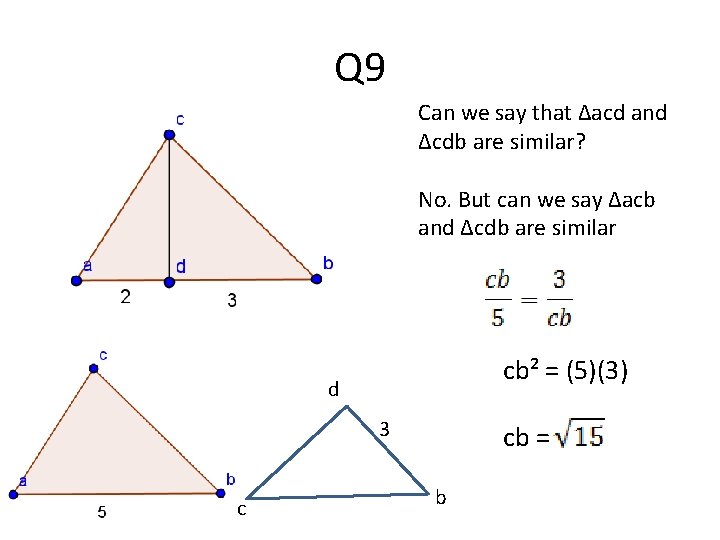
Q 9 Can we say that ∆acd and ∆cdb are similar? No. But can we say ∆acb and ∆cdb are similar cb² = (5)(3) d 3 c cb = b