Geometry 12 2 12 3 Arcs and Chords

Goals o Identify arcs & chords in circles o Compute arc measures and angle

Central Angle A 08 June 2021 An angle whose vertex is the center of

Minor Arc C A 08 June 2021 Part of a circle. The measure of

Semicircle C A D 08 June 2021 Half of a circle. The endpoints of

Major Arc C A D 08 June 2021 T Part of a circle. The

Measuring Arcs o An arc has the same measure as the central angle. o

Measuring Major Arcs o The measure of an major arc is given by 360

Arc Addition Postulate Demonstration R T 08 June 2021 C A

What have you learned so far? o o o o o Page 607 Do

Subtending Chords A O C 08 June 2021 Chord AB subtends AB. B Chord

Theorem 12. 4 o Two minor arcs are congruent if and only if corresponding

Example Solve for x. 120 (5 x + 10) 5 x + 10 =

Theorem 12. 5 o If a diameter is perpendicular to a chord, then it

Example Solve for x. 52 2 x 08 June 2021 2 x = 52

Theorem 12. 6 o If a chord is the perpendicular bisector of another chord,

Theorem 12. 7 o Two chords are congruent if and only if they are

The red wires are the same length because they are the same distance from

Example 16 Solve for x. 4 x – 2 = 16 4 x =

Summary o Chords in circles subtend major and minor arcs. o Arcs have the

Slides: 24

Download presentation

Geometry 12. 2 -12. 3 Arcs and Chords

Goals o Identify arcs & chords in circles o Compute arc measures and angle measures 08 June 2021

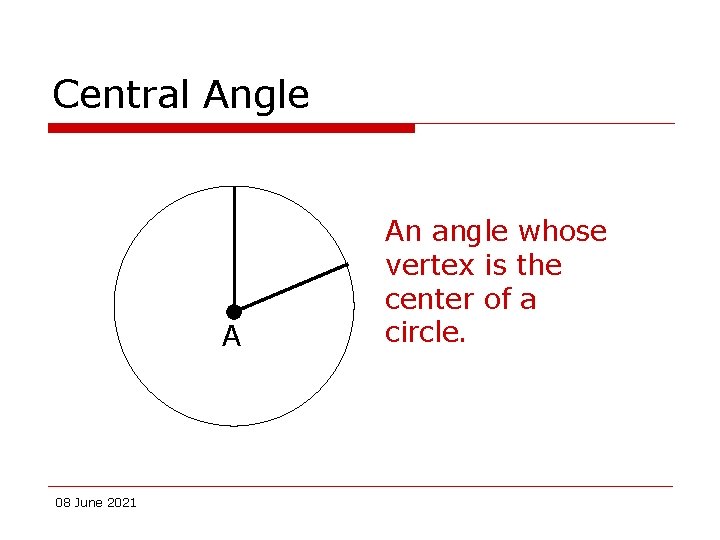
Central Angle A 08 June 2021 An angle whose vertex is the center of a circle.

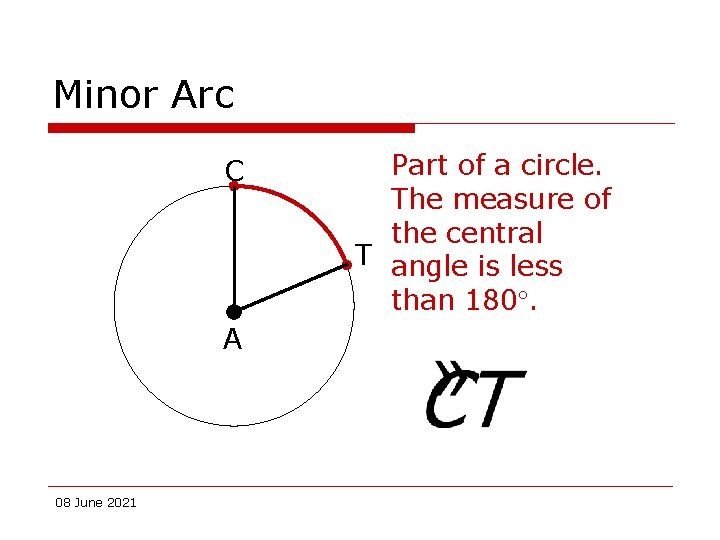
Minor Arc C A 08 June 2021 Part of a circle. The measure of the central T angle is less than 180.

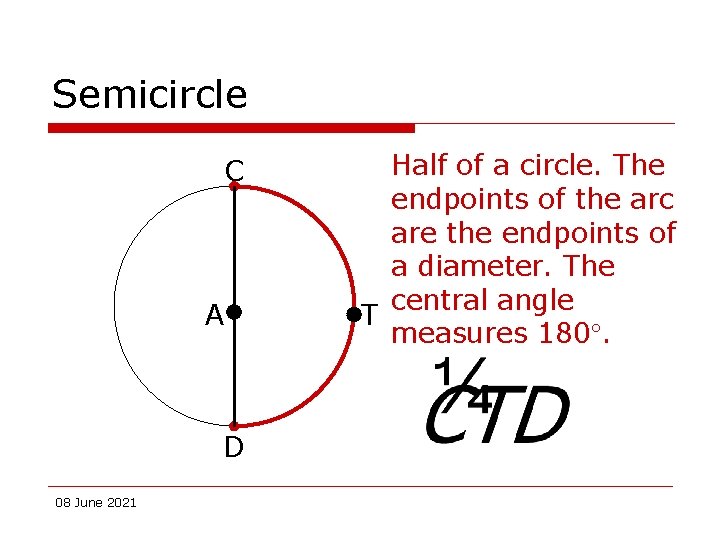
Semicircle C A D 08 June 2021 Half of a circle. The endpoints of the arc are the endpoints of a diameter. The central angle T measures 180.

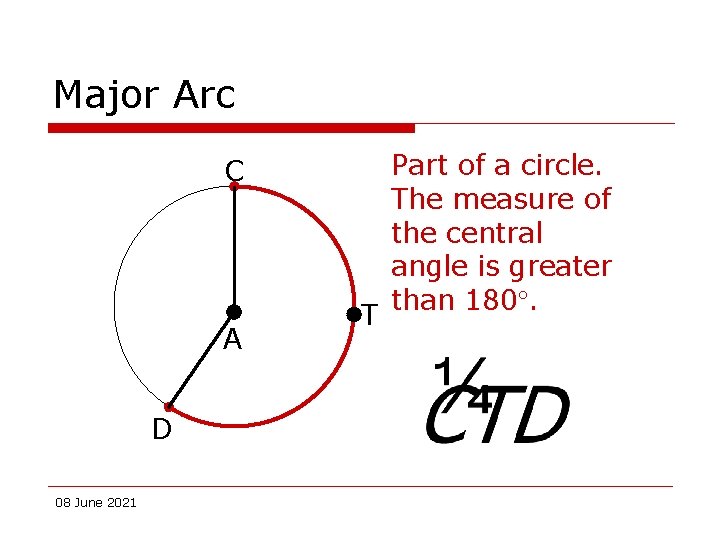
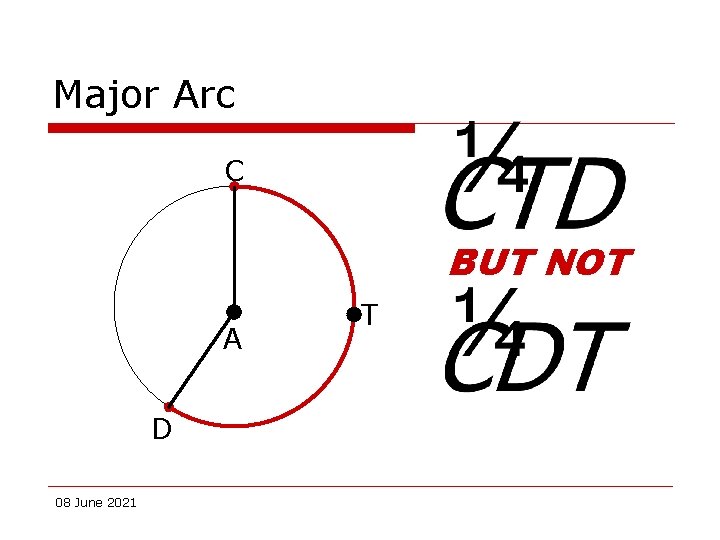
Major Arc C A D 08 June 2021 T Part of a circle. The measure of the central angle is greater than 180.

Major Arc C BUT NOT A D 08 June 2021 T

Measuring Arcs o An arc has the same measure as the central angle. o We say, “a central angle subtends an arc of equal measure”. A 42 42 C B Central Angle Demo 08 June 2021

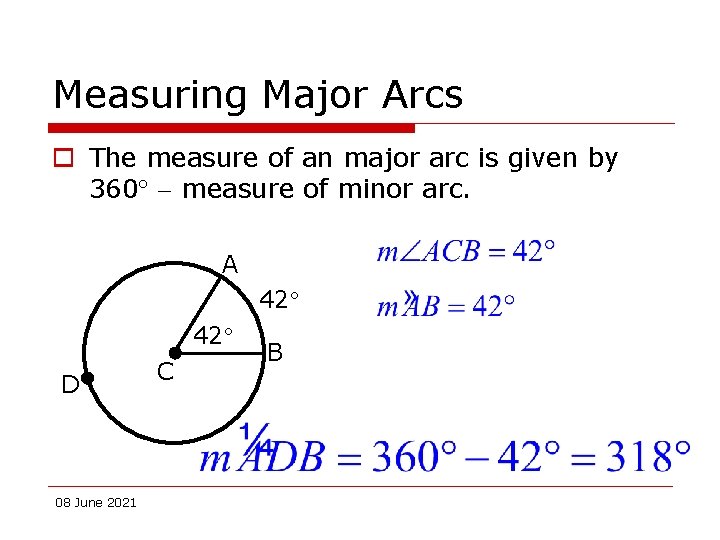
Measuring Major Arcs o The measure of an major arc is given by 360 measure of minor arc. A 42 42 D 08 June 2021 C B

Arc Addition Postulate Demonstration R T 08 June 2021 C A

What have you learned so far? o o o o o Page 607 Do problems 3 – 8. Answers… 3) 4) 5) 6) 7) 8) 08 June 2021 Q T 40 R 60 S P 120

Subtending Chords A O C 08 June 2021 Chord AB subtends AB. B Chord BC subtends BC.

08 June 2021

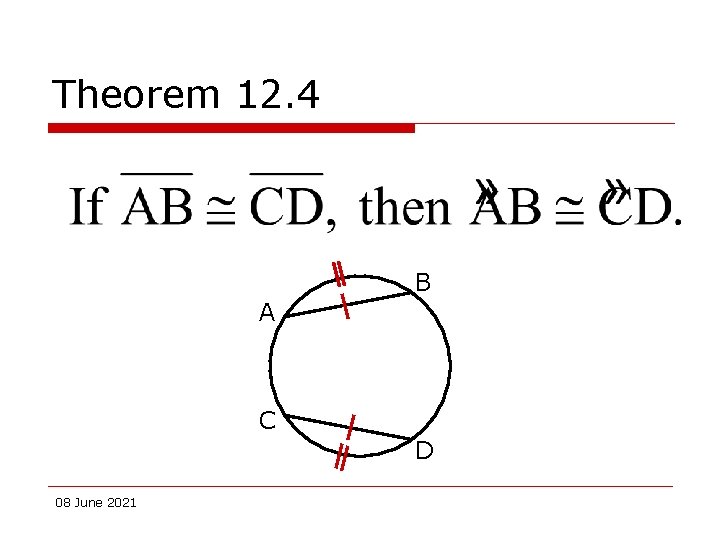
Theorem 12. 4 o Two minor arcs are congruent if and only if corresponding chords are congruent. 08 June 2021

Theorem 12. 4 B A C D 08 June 2021

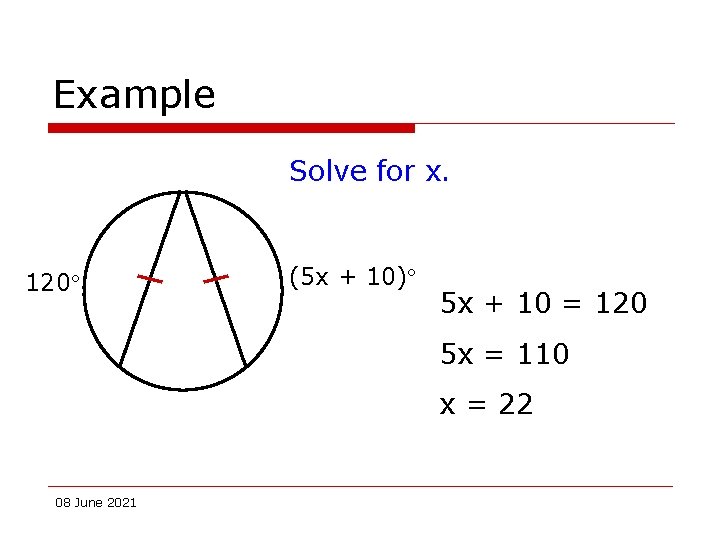
Example Solve for x. 120 (5 x + 10) 5 x + 10 = 120 5 x = 110 x = 22 08 June 2021

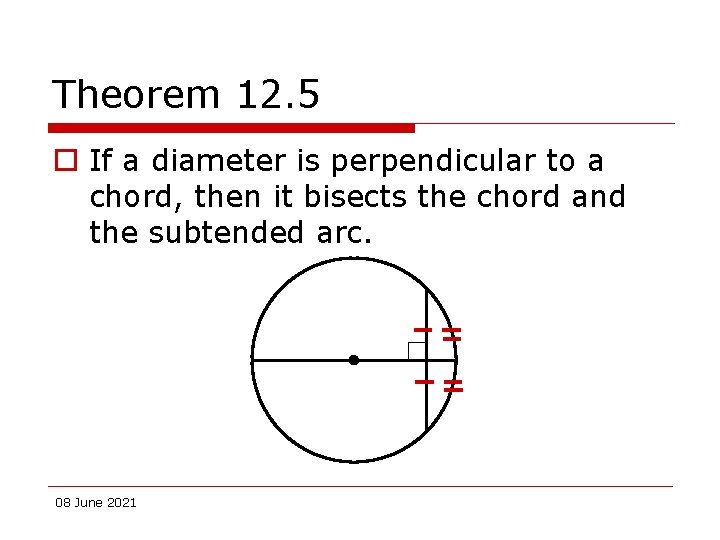
Theorem 12. 5 o If a diameter is perpendicular to a chord, then it bisects the chord and the subtended arc. 08 June 2021

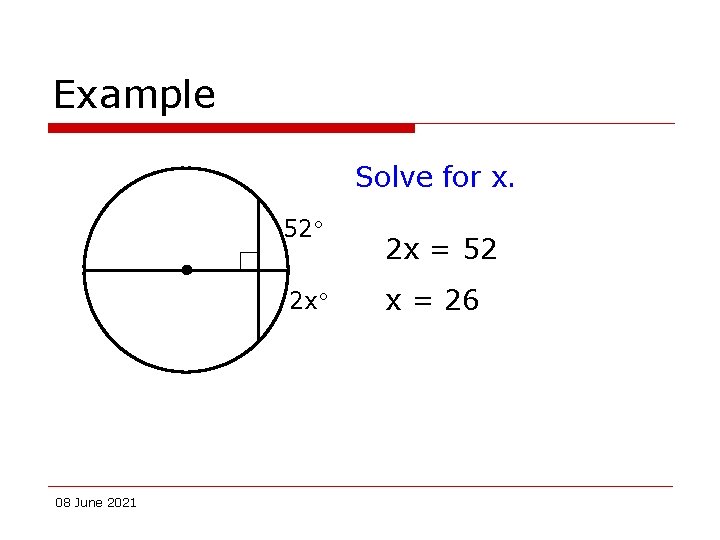
Example Solve for x. 52 2 x 08 June 2021 2 x = 52 x = 26

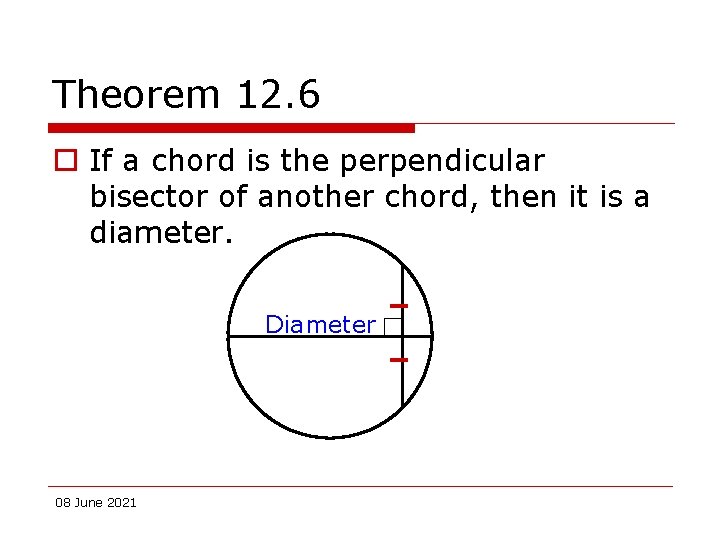
Theorem 12. 6 o If a chord is the perpendicular bisector of another chord, then it is a diameter. Diameter 08 June 2021

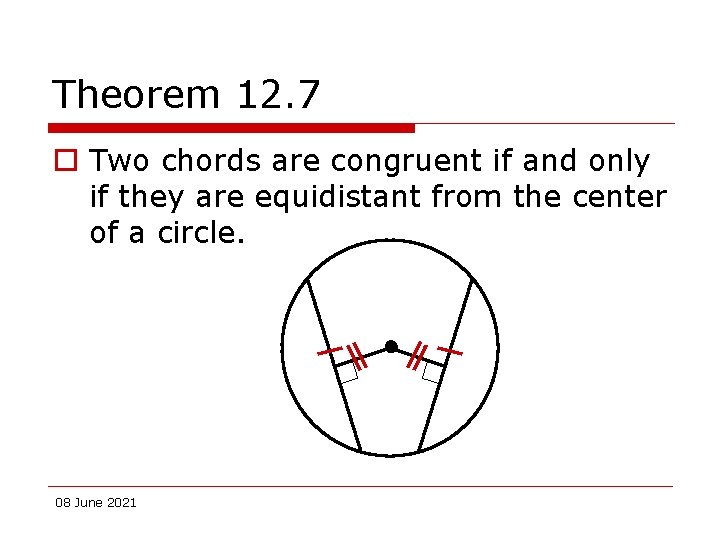
Theorem 12. 7 o Two chords are congruent if and only if they are equidistant from the center of a circle. 08 June 2021

The red wires are the same length because they are the same distance from the center of the grate. 08 June 2021

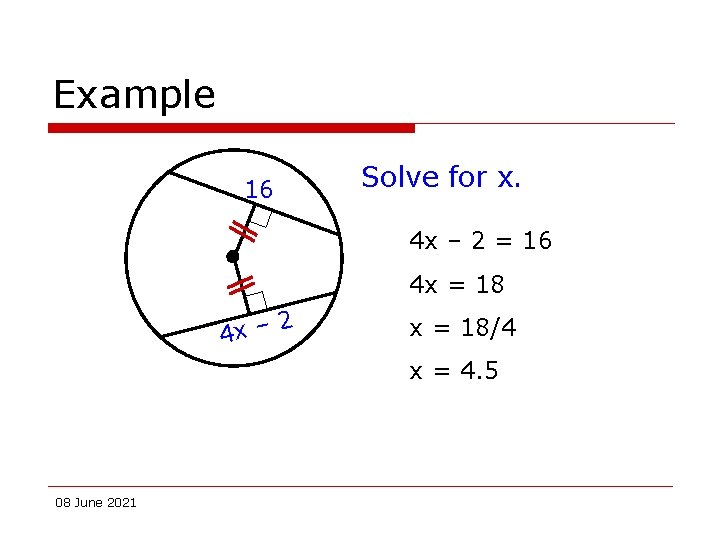
Example 16 Solve for x. 4 x – 2 = 16 4 x = 18 2 4 x – x = 18/4 x = 4. 5 08 June 2021

Summary o Chords in circles subtend major and minor arcs. o Arcs have the same measure as their central angles. o Congruent chords subtend congruent arcs and are equidistant from the center. o If a diameter is perpendicular to a chord, then it bisects it. 08 June 2021

Practice Problems 08 June 2021