GEOMETRIJA U RAVNI OSNOVNI I IZVEDENI POJMOVI I

GEOMETRIJA U RAVNI OSNOVNI I IZVEDENI POJMOVI I STAVOVI U GEOMETRIJI Osnovni pojmovi u geometriji su: tačka, prava i ravan. Osnovni relacije su: izmeđ i podudarno. Tačke označavamo velikim slovima: A, B, C, . . . P, Q, . . Prave označavamo malim slovima: a, b, c, . . . . p, q, . . Ravni označavamo sagrčkim slovima: λ, β, γ, δ Podudarno označavamo: ≅ Između označavamo : A-B-C ( tačka A je između tačaka B i C ) Nove pojmove uvodimo definicijama koristećise osnovnim pojmovima i pojmovima koje smo već definisali.

AKSIOME PRAVE: A 1: Svake dvije različite tačke određuju samo jednu pravu ( Kroz dvije tačke prolazi uvijek jedna i samo jedna prava) A 2: Svaka prava sadrži najmanje dvije različite tačke A 3: Postoje tri tačke koje ne pripadaju jednoj pravoj. (Postoji bar jedna tačka koja ne pripada datoj pravoj ) Definišimo sada neke pojmove koje ćemo koristiti u daljem izlaganju: Def: Za dvije prave koje imaju jednu zajedničku tačku kažemo da se sijeku. Def: Za tačke koje pripadaju istoj pravoj kažemo da su kolinearne, a za tačke koje ne pripadaju istoj pravoj kažemo da su nekolinearne.

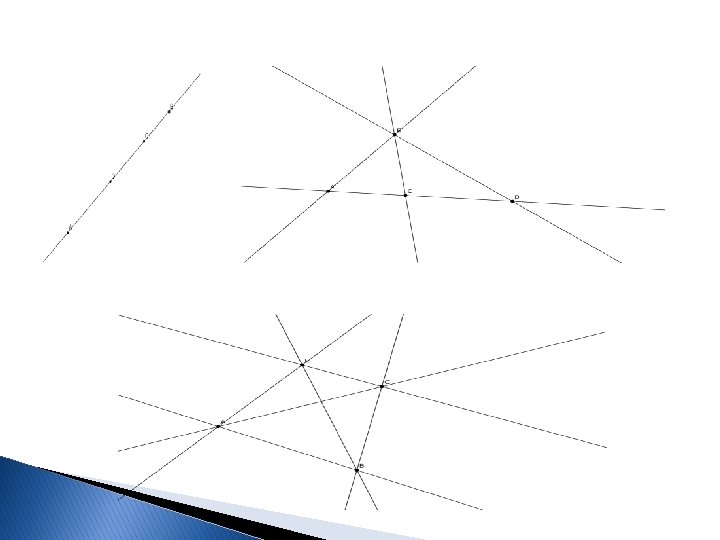
PRIMJER: Koliko različitih pravi određuju četiri različite tačke A, B, C, D Rješenje: Posmatraćemo nekoliko slučajeva: a) Sve tačke su kolinearne – imamo samo jednu pravu b) Tri tačke kolinearne (A, C, D) – imamo 4 različite prave kroz tačke ACD; BA; BC ; BD: c) Sve četiri tačke nekolinearne: imamo 6 različitih pravih AB; AC; AD; BC; BD; CD

PRIMJER 2: Dato nam je n tačaka od kojih nikoje tri nisu kolinearne. Koliko pravih one određuju? Rješenje: uzmemo prvu tačku ( recimo A ) tada ona sa svakom od preostalih tačaka određuje najviše po jednu pravu , dakle (n-1) pravih. Sada uzmemo drugu tačku i izvedemo isti zaključak, i tako do posljednje tačke. U ovom postupku primjetićemo da ćemo imati između svake dvije tačke po dvije prave ( recimo AB i BA ) ali to su prave koje se poklapaju, pa možemo reči da će broj pravih ukupno biti n(n-1) podijeljeno sa 2. Dakle formula po kojoj ćemo izračunati broj pravih koje obrazuje n tačaka je :

AKSIOME RAVNI A 4: Svake tri nekolinearne tačke određuju samo jednu ravan. ( Kroz tri nekolinearne tačke prolazi jedna i samo jedna ravan. ) A 5: Svaka ravan sadrži bar tri nekolinearne tačke. A 6: Postoje bar četiri tačke koje ne pripadaju istoj ravni. Def: Za tačke koje leže u jednoj ravni kažemo da su komplanarne. Za četiri tačke koje ne leže u istoj ravni kažemo da su nekomplanarne.

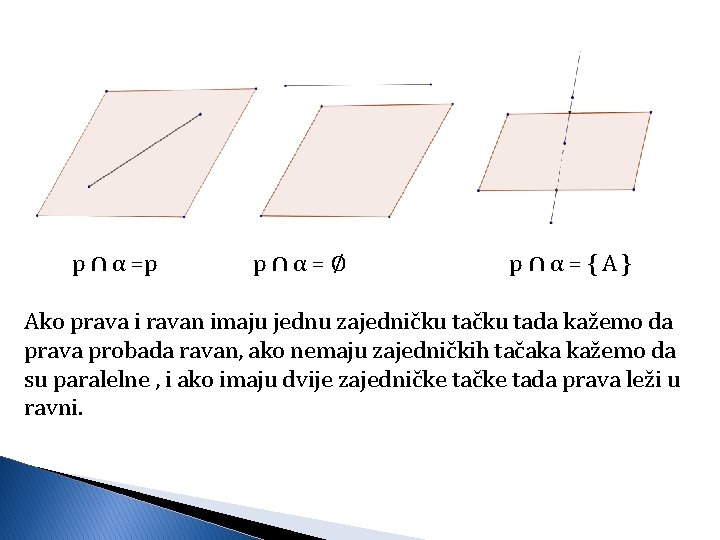
AKSIOME PRAVE I RAVNI A 7: Ako dvije tačke jedne prave pripadaju ravni α tada sve tačke te pravepripadaju ravni α. Def: Ako sve tačke prave p pripadaju ravni α , kažemo da prava p leži u ravni α i zapisujemo p⊂α. Teorema : Ravan i prava koja nije sadržana u toj ravni mogu imati najviše jednu zajedničku tačku. Iz svega navedenog zaključujemo da mogu postojati tri međusobna odnosa između prave i ravnia. p ∩ α =p p∩α=∅ p∩α={A}

p ∩ α =p p∩α=∅ p∩α={A} Ako prava i ravan imaju jednu zajedničku tada kažemo da prava probada ravan, ako nemaju zajedničkih tačaka kažemo da su paralelne , i ako imaju dvije zajedničke tada prava leži u ravni.

ODREĐENOST RAVNI Teorema 1: Postoji jedna i samo jedna ravan koja sadrži dvije prave koje se sijeku. ( Ravan je određena sa dvije prave koje se sijeku. ) Teorema 2: Postoji jedna i samo jedna ravan koja sadrži datu pravu i datu tačku koja ne pripada toj pravoj. ( Ravan je određena sa pravom i tačkom van te prave. )

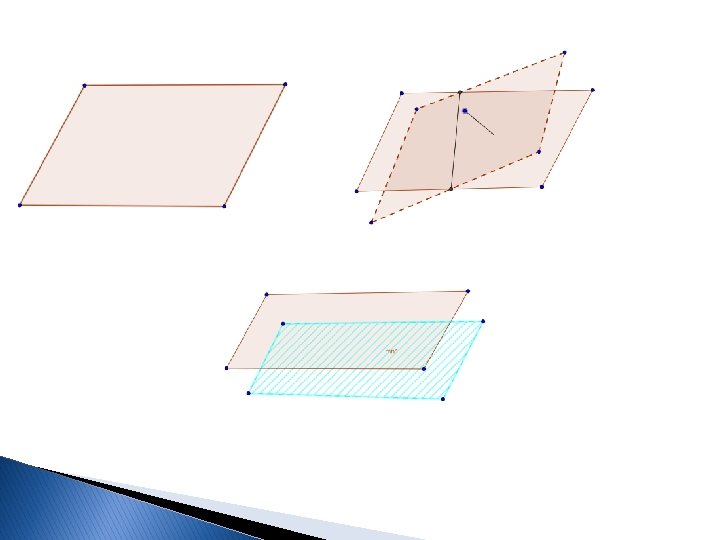
AKSIOMA O DVIJE RAVNI A 8: Ako dvije ravni imaju jednu zajedničku tačku onda one imaju još jednu zajedničku tačku. Odavde zaključujemo da ako dvije ravni imaju jednu zajedničku tačku onda one imaju zajedničku pravu. Iz ove aksiome slijedi da su moguća svega tri uzajamna položaja dvije ravni. a) Ako ravni α i β imaju tri zajedničke nekolinearne tačke tada je α = β b) Ako α i β imaju zajedničku tada je α ∩ β = p i kažemo da se ravni α i β sijeku po pravoj p c) Ako ravni α i β nemaju zajedničkih tačaka tj ako je α ∩ β =∅ , tada su α i β paralelne što označavamo sa α ∥ β.

AKSIOMA PARALELNOSTI DVIJE RAVNI Def: Za dvije prave p q koje leže u istoj ravni kažemo da su paralelne i zapisujemo p ∥ q ako je p=q ili p ∩ q = ∅. A 9: Ako tačka A i prava p pripadaju istoj ravni α , onda tačkom A prolazi tačno jedna prava koj pripada ravni α iparalelna je sa pravom p. Teorema: Postoji tačno jedna ravan koja sadrži dvije date paralelne prave. ( Ravan je određena sa dvije različite paralelne prave ) Tore ma : Ako prave p q i r leže u jednoj ravni α i ako su prave p i q paralelne i ako prava r siječe pravu p tada ona siječe i pravu q.