Geometrically Stable Sampling for the ICP Algorithm 10242020

Geometrically Stable Sampling for the ICP Algorithm 10/24/2020 Natasha Gelfand Leslie Ikemoto Stanford University UC Berkeley Szymon Rusinkiewicz Marc Levoy Princeton University Stanford University 1

Two Flavors of ICP • Point-point error • Point-plane error • faster to converge ni qi 10/24/2020 pi qi pi 2

Source of Failures • • Complex error landscape Many local minima Usually have to start from a good guess Point selection and error metric in minimization are key to convergence • Some shapes are particularly “difficult” • Noise 10/24/2020 3

Requirements for Error Metric • Planar and spherical areas with no features should not contribute to distance metric • “Lock and key” features should pull the surfaces to correct relative pose • Robust even as features get small and featureless regions noisy 10/24/2020 4

Solution • Detect when parts of the input patch are prone to sliding • Use covariance analysis • Concentrate samples in “lock and key” areas to improve convergence • Use geometrically stable point-selection strategy • Similar to normal-space sampling [Rusinkiewicz & Levoy] • Detect when input has no “lock and key” features • Do not align that scan pair at all • Improves convergence of global registration [Ikemoto et. al] 10/24/2020 5

Minimization Equation • Find (R, t) that minimize ni • Linearizing rotations: find r=[rx ry rz]T, t=[tx ty tz]T that minimize 10/24/2020 qi pi 6

Analyzing the Metric (1) • Change in error from each point-pair: “torque” “force” • For some transformations e=0: P Q 10/24/2020 P translation perpendicular to “force” Q 7

Analyzing the Metric (2) • Change in error from each point-pair: “torque” “force” • For some transformations e=0: P 10/24/2020 Q P Q rotation perpendicular to “torque” 8

Covariance Matrix • Aligning transform is given by Cx=b, where • C encodes the change in error when surfaces are moved from optimal alignment 10/24/2020 9

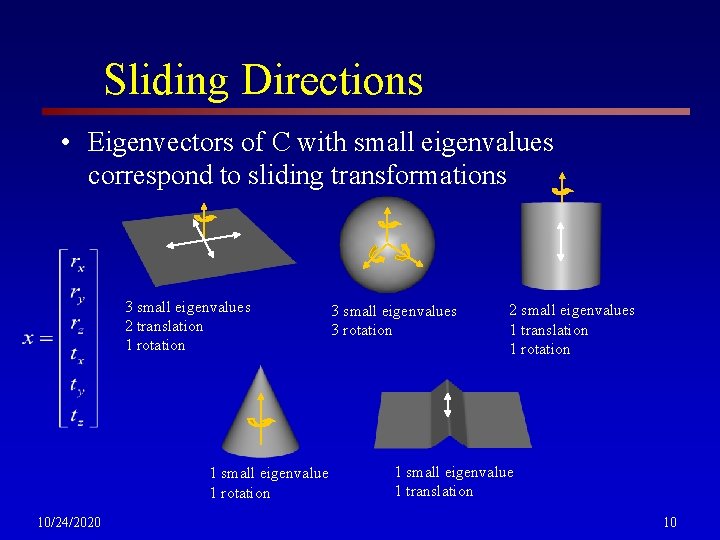
Sliding Directions • Eigenvectors of C with small eigenvalues correspond to sliding transformations 3 small eigenvalues 2 translation 1 rotation 1 small eigenvalue 1 rotation 10/24/2020 3 small eigenvalues 3 rotation 2 small eigenvalues 1 translation 1 rotation 1 small eigenvalue 1 translation 10

Sample Selection • Goal of sampling is to produce covariance matrix C with a good condition number • Equally constrain all eigenvectors • Find points that well sample the small features on P • Since P and Q are similar in the overlap region, use both points and normals from P to compute C 10/24/2020 11

Implementation (1) • Estimate C from sparse uniform sampling of input mesh • C = X LX T • • • 10/24/2020 6 x 6 matrix 6 eigenvectors form basis for the space of transforms 12

Implementation (2) • For each point form • For each eigenvector x j compute • Magnitude of the constraint pi exerts on x j • Sort points in decreasing “order of influence” for each eigenvector 10/24/2020 x 1 x 2 x 3 x 4 x 5 x 6 p 1 p 8 p 3 p 5 p 2 p 7 p 6 p 3 p 3 p 5 p 8 p 7 p 1 p 4 … p 9 … p 8 … p 7 … 13

Implementation (3) • Let be an estimate of how well eigenvector x j is constrained by already chosen points • Choose next pi from list with the smallest corresponding t j • Most unconstrained eigenvector • Compute closest point qi in Q • Once enough points are chosen, solve for alignment and iterate 10/24/2020 14

Sample Selection • Small eigenvalues 10/24/2020 15

Sample Selection • Large eigenvalues 10/24/2020 16

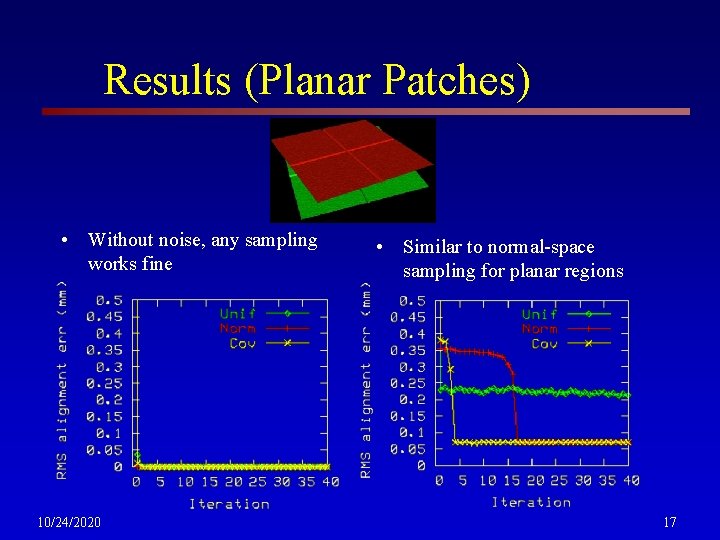
Results (Planar Patches) • Without noise, any sampling works fine 10/24/2020 • Similar to normal-space sampling for planar regions 17

Results (Planar Patches) uniform sampling stable sampling • 25 iterations to converge • Naïve implementation about 3 times slower per iteration than uniform sampling 10/24/2020 18

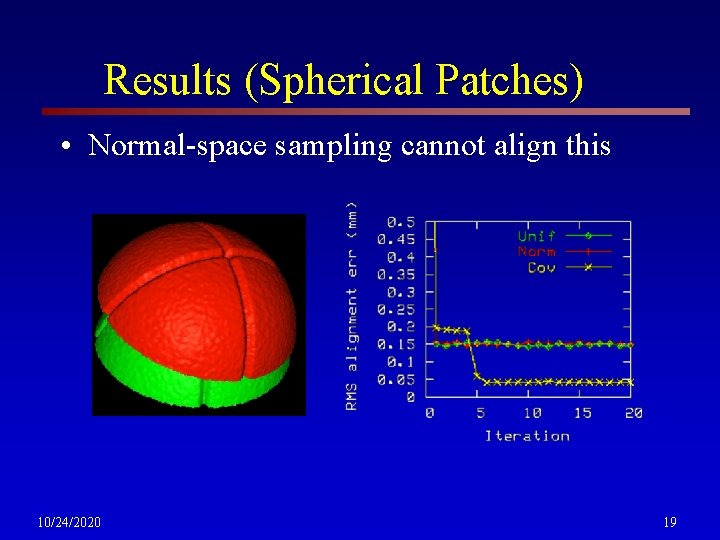
Results (Spherical Patches) • Normal-space sampling cannot align this 10/24/2020 19

Conclusions • Point-plane error metric can have shallow error landscape when registering shapes with small features • Noise adds many small local minima • These conditions can be detected by analyzing the covariance matrix of the minimization equation • Eigenvectors with small eigenvalues give sliding directions • Stable sampling improves these landscapes by equally constraining all eigenvectors • Selects point samples inside the features • Allows ICP to align “difficult” input 10/24/2020 20

Limitations: Noise • The algorithm can fail if input data is particularly noisy • Smoothing can help 10/24/2020 21

Limitations: Noise • Success depends on relative size of features 10/24/2020 22

Extensions and Future Work • Use stability analysis to weigh mesh pairs in global registration • A hierarchical method for aligning warped meshes [Ikemoto et al] • Stable sampling for global registration • Simultaneous covariance analysis of the entire set of scans • Weighing eigenvectors based on the area outside the overlap • Large vs. small leverage on the entire scan 10/24/2020 23

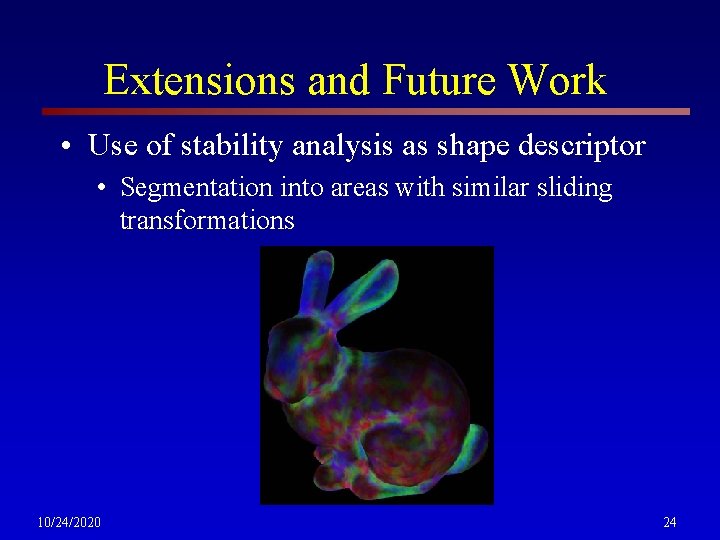
Extensions and Future Work • Use of stability analysis as shape descriptor • Segmentation into areas with similar sliding transformations 10/24/2020 24