Geometrical Transformation TongYee Lee positive rotation 1 3

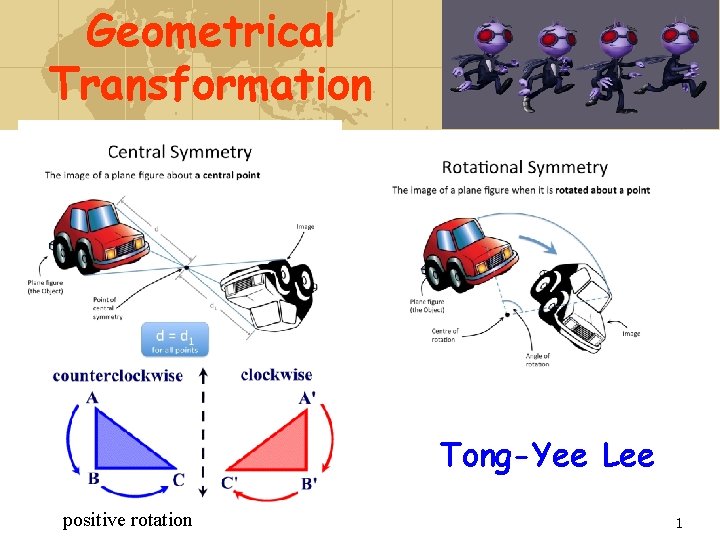
Geometrical Transformation Tong-Yee Lee positive rotation 1

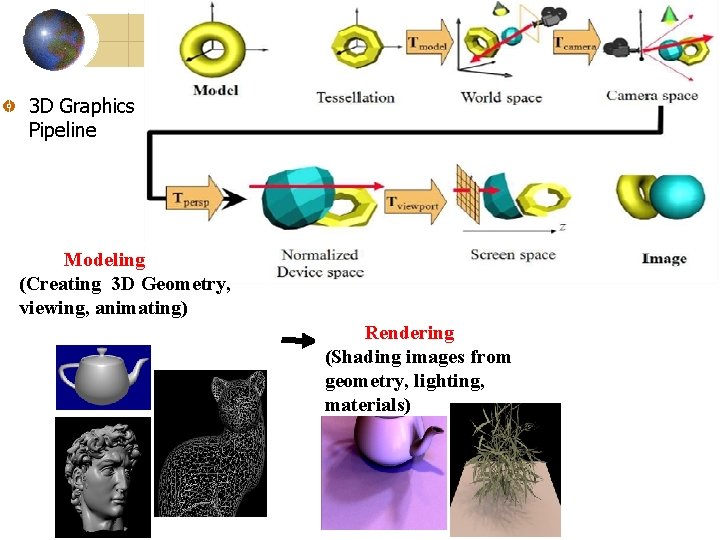
3 D Graphics Pipeline Modeling (Creating 3 D Geometry, viewing, animating) Rendering (Shading images from geometry, lighting, materials)

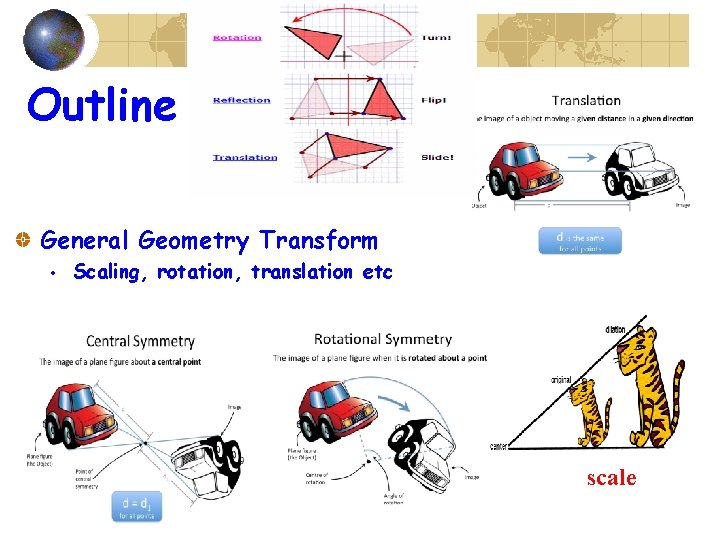
Outline General Geometry Transform • Scaling, rotation, translation etc scale

Modeling Transform Specify transformation for objects Allow definitions of objects in own local coordinate systems Allow use of object definition multiple times in a scene Insert each local object into different locations of world coordinate 4

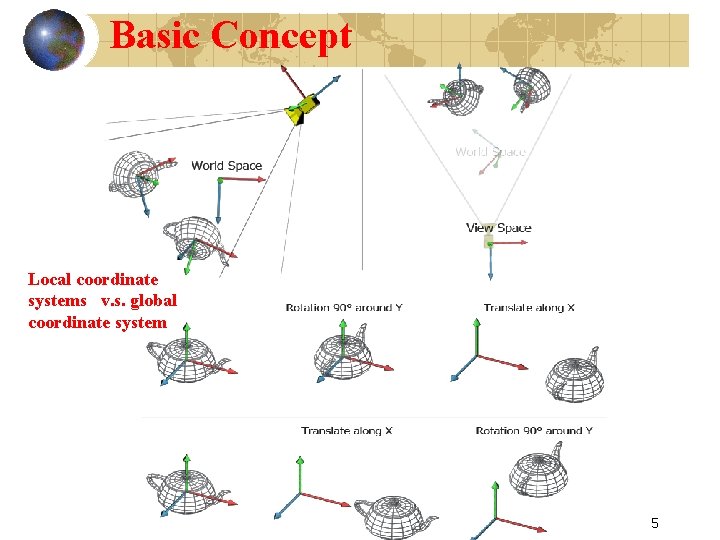
Basic Concept Local coordinate systems v. s. global coordinate system 5

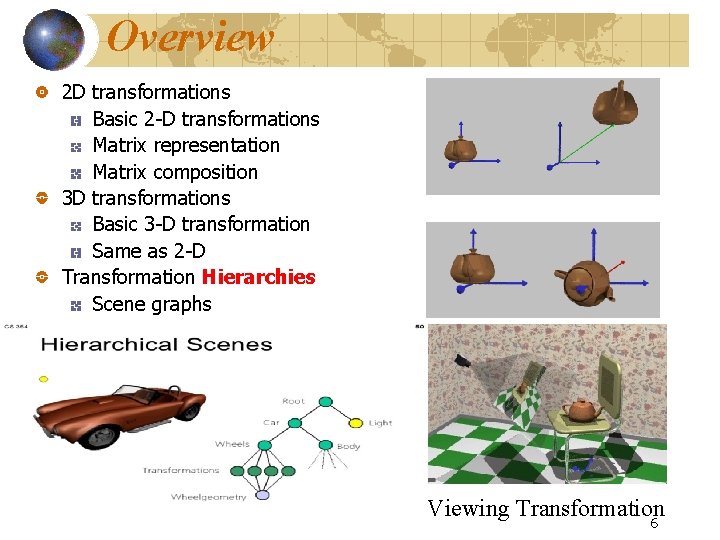
Overview 2 D transformations Basic 2 -D transformations Matrix representation Matrix composition 3 D transformations Basic 3 -D transformation Same as 2 -D Transformation Hierarchies Scene graphs Viewing Transformation 6

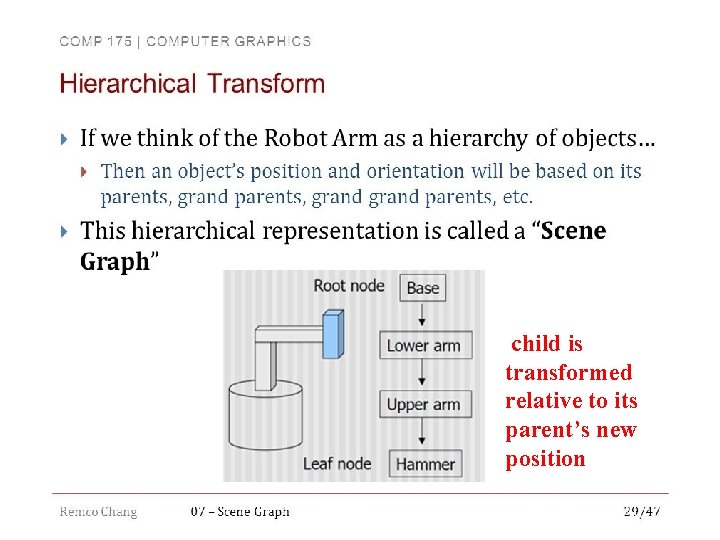
child is transformed relative to its parent’s new position 7

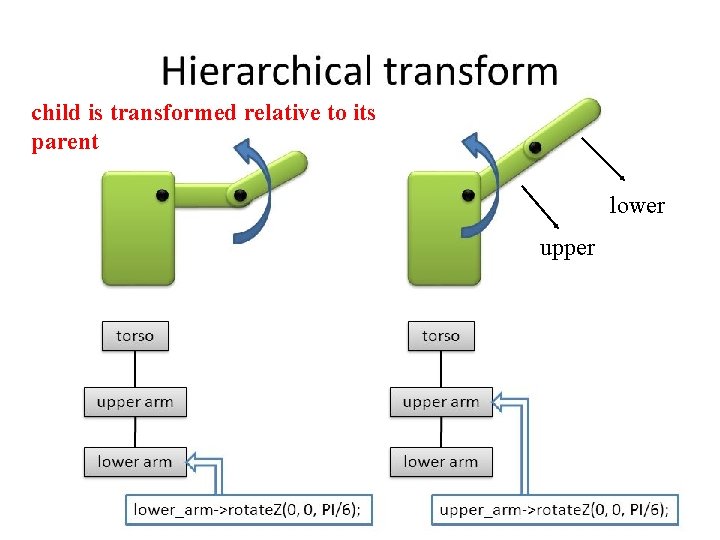
child is transformed relative to its parent lower upper 8

9

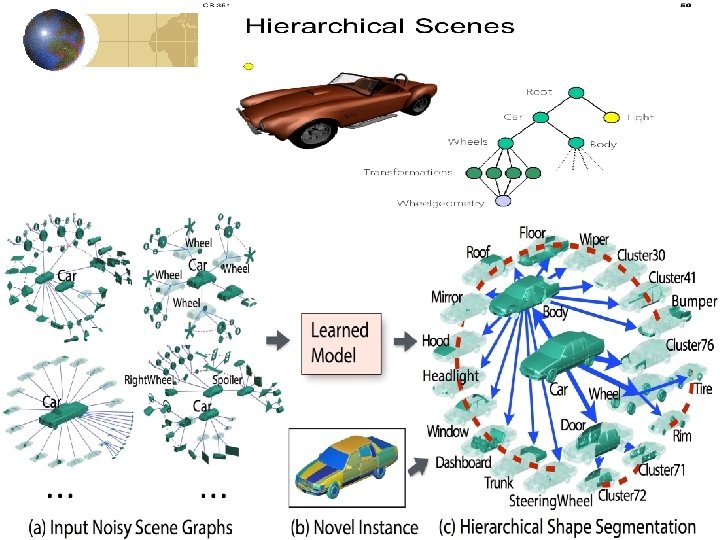
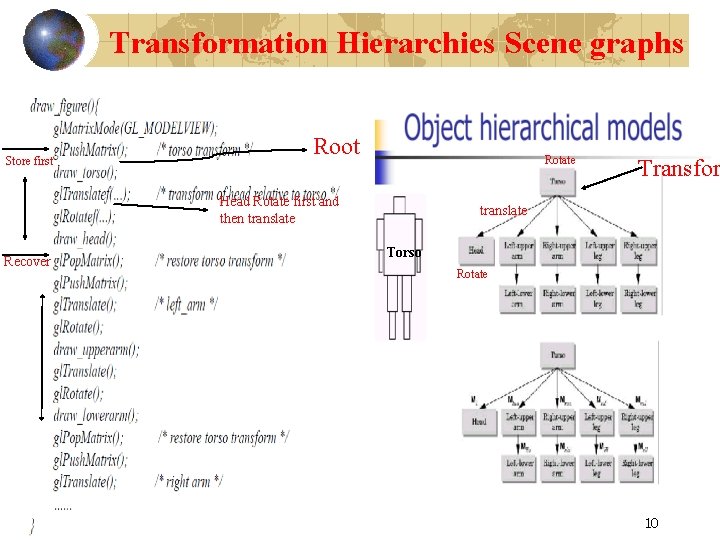
Transformation Hierarchies Scene graphs Store first Root Rotate Head Rotate first and then translate Recover Transfor translate Torso Rotate 10

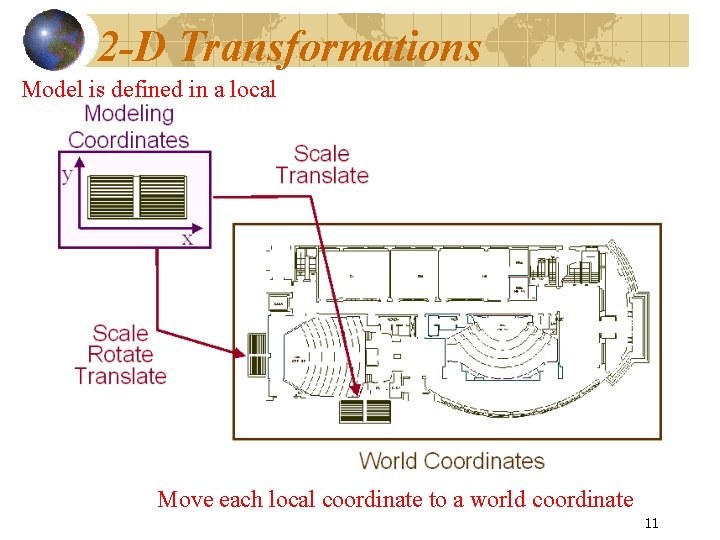
2 -D Transformations Model is defined in a local Move each local coordinate to a world coordinate 11

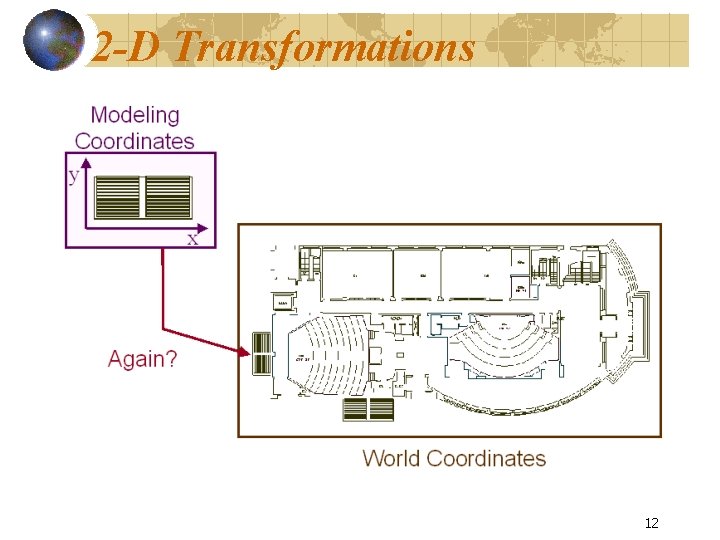
2 -D Transformations 12

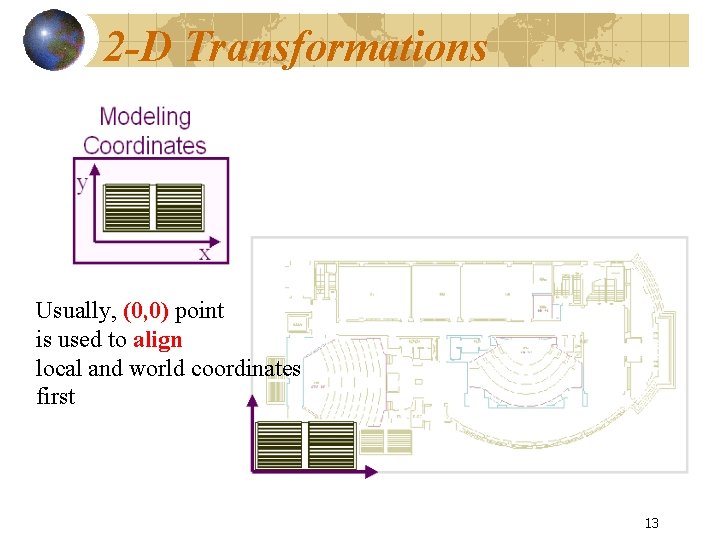
2 -D Transformations Usually, (0, 0) point is used to align local and world coordinates first 13

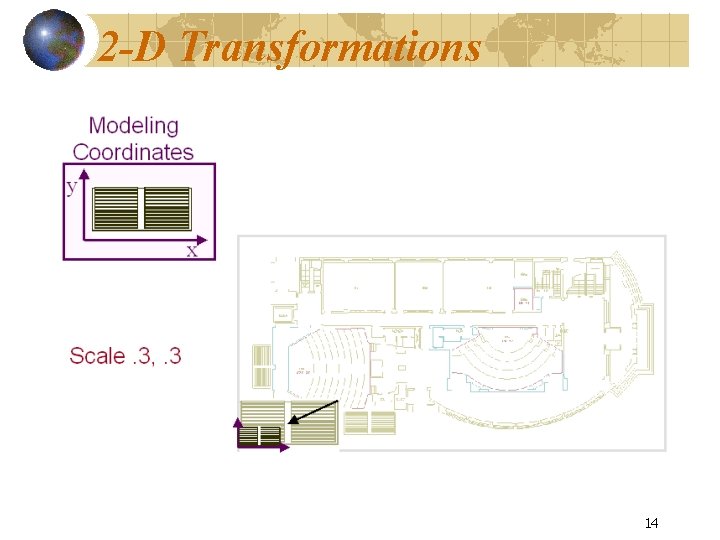
2 -D Transformations 14

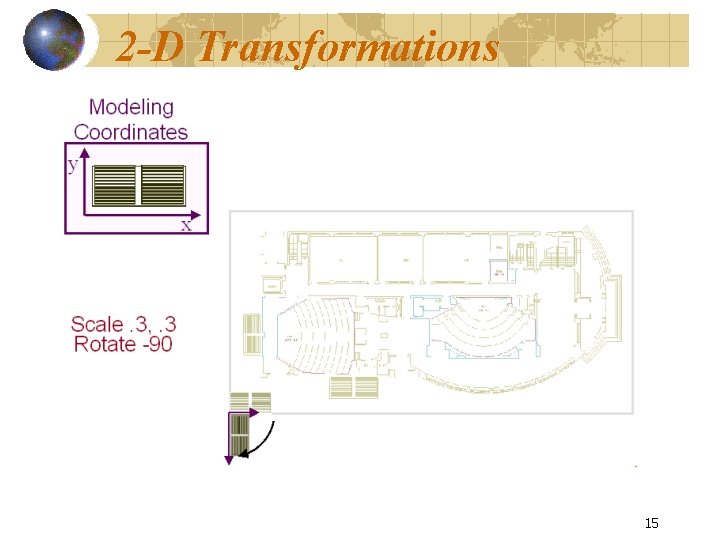
2 -D Transformations 15

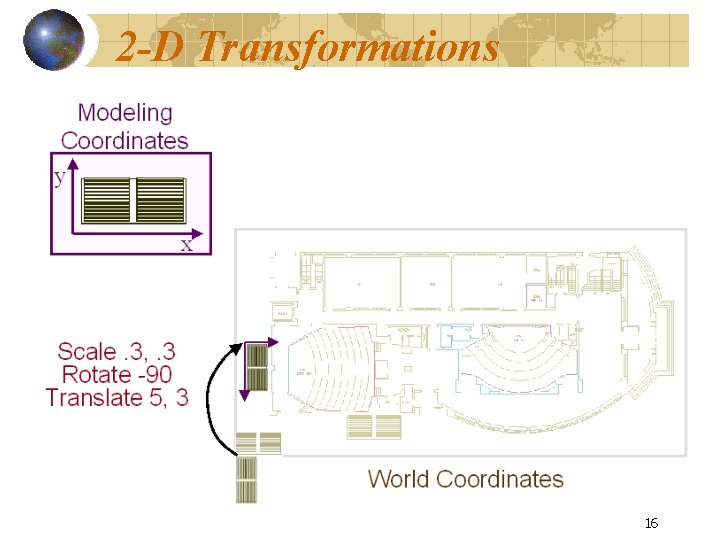
2 -D Transformations 16

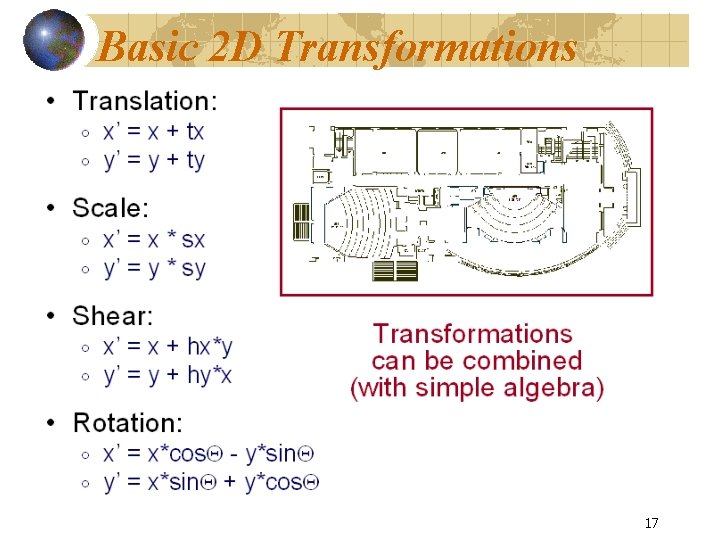
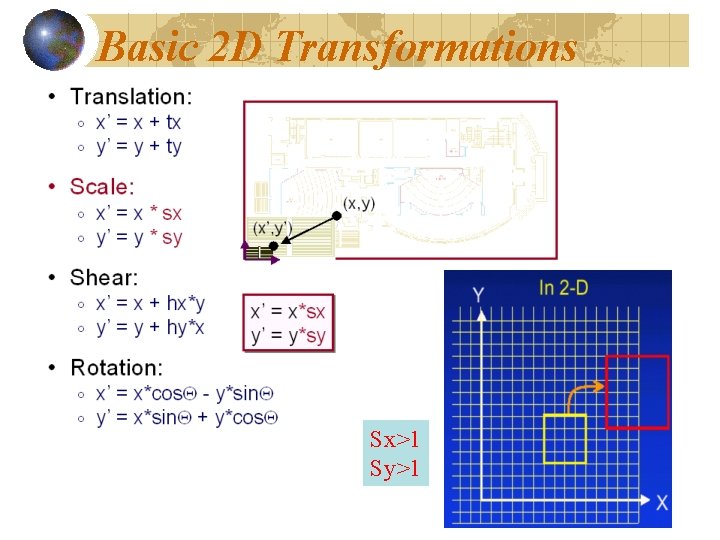
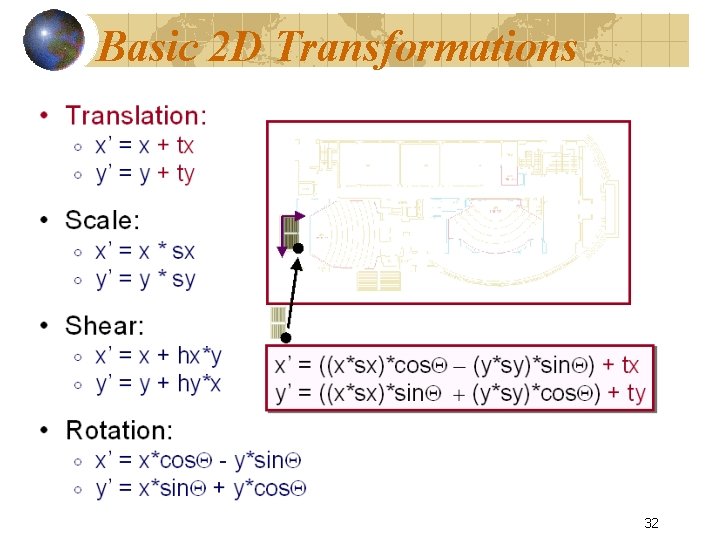
Basic 2 D Transformations 17

Basic 2 D Transformations Sx>1 Sy>1 18

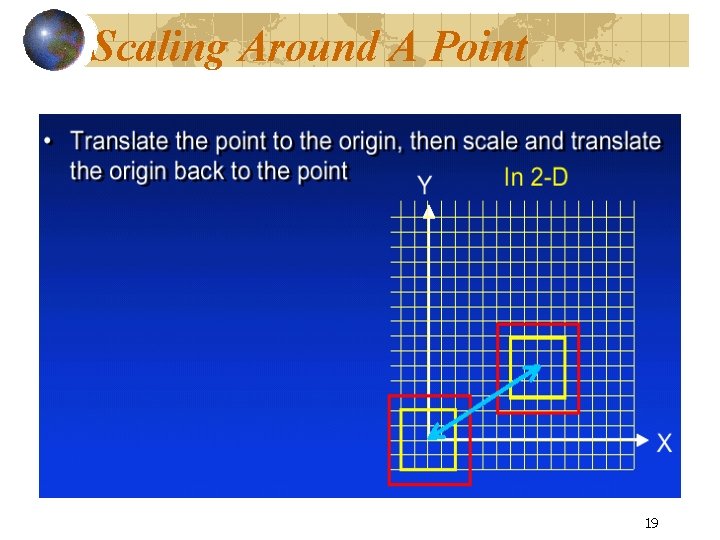
Scaling Around A Point 19

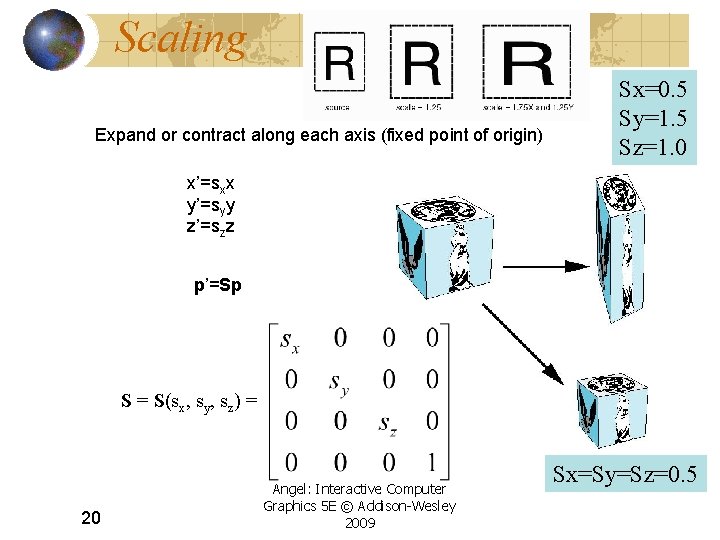
Scaling Expand or contract along each axis (fixed point of origin) Sx=0. 5 Sy=1. 5 Sz=1. 0 x’=sxx y’=syy z’=szz p’=Sp S = S(sx, sy, sz) = 20 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009 Sx=Sy=Sz=0. 5

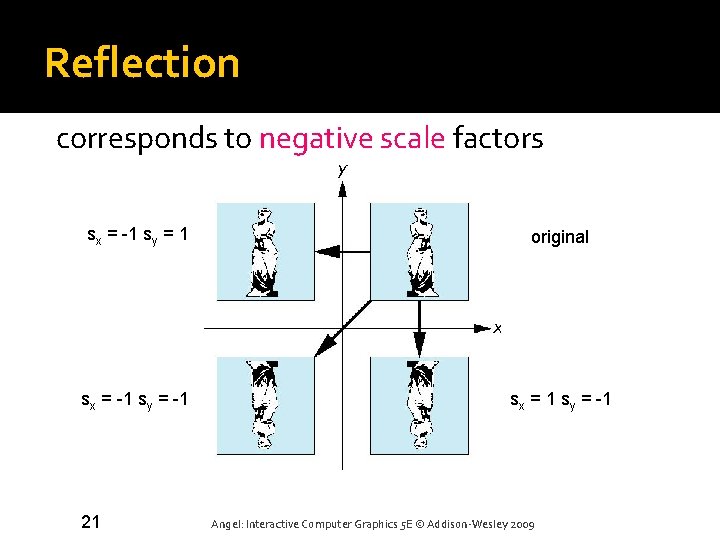
Reflection corresponds to negative scale factors sx = -1 sy = 1 original sx = -1 sy = -1 sx = 1 sy = -1 21 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

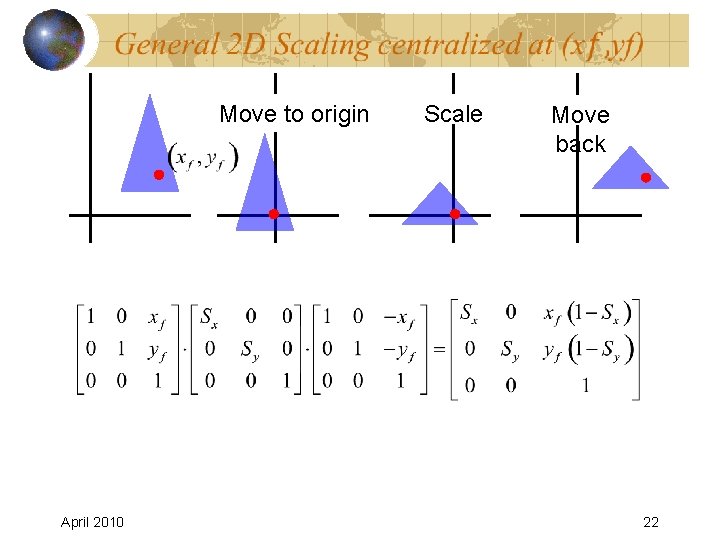
Move to origin April 2010 Scale Move back 22

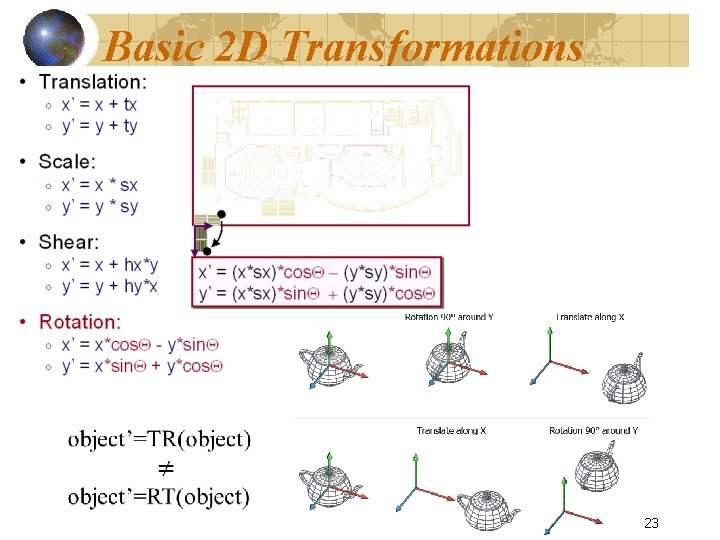
Basic 2 D Transformations 23

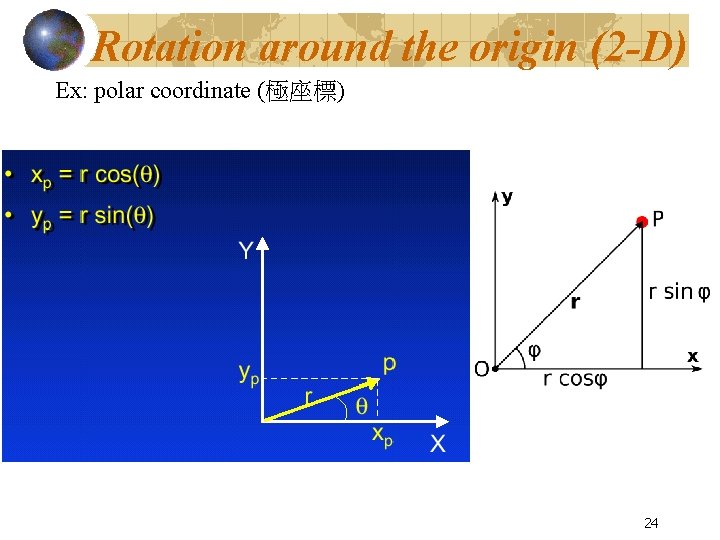
Rotation around the origin (2 -D) Ex: polar coordinate (極座標) 24

Rotation around the origin (2 -D) Counterclockwise i. e. , 逆時針方向 (positive) 25

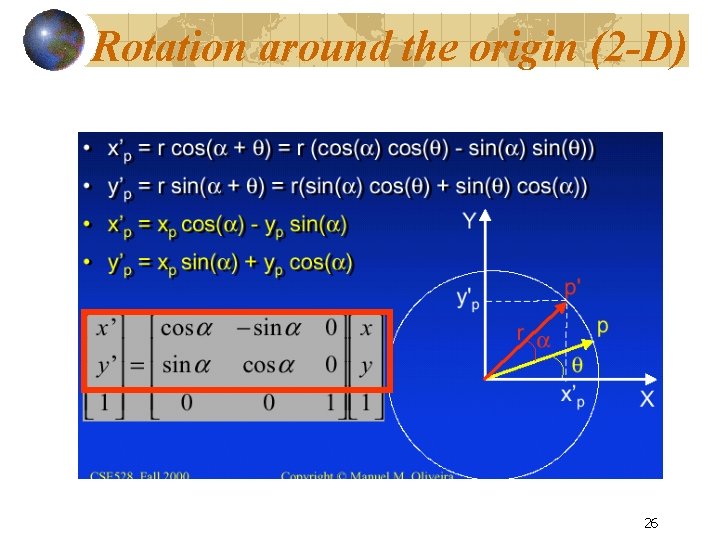
Rotation around the origin (2 -D) 26

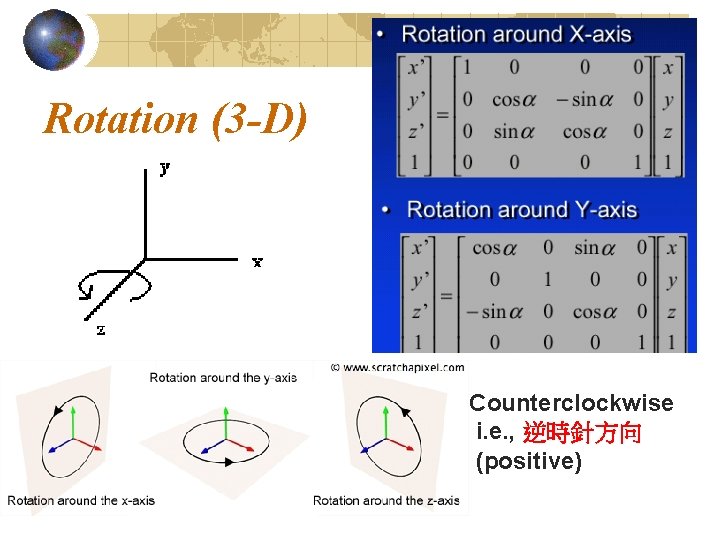
Rotation (3 -D) 27

Rotation (3 -D) Counterclockwise i. e. , 逆時針方向 (positive)

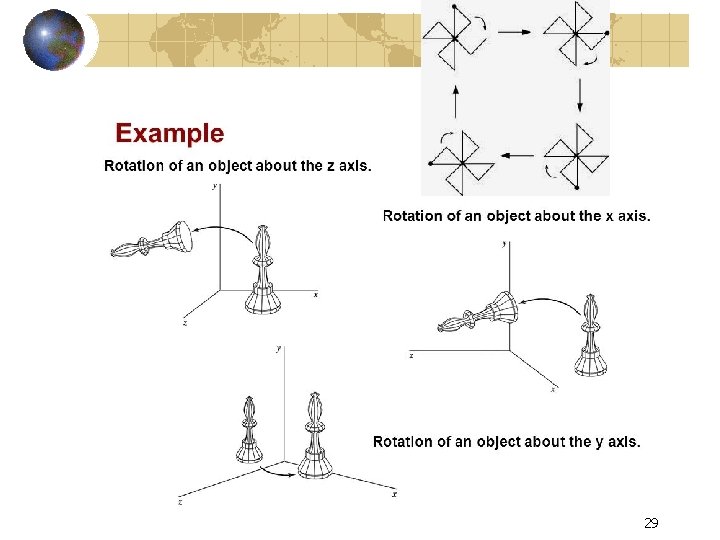
29

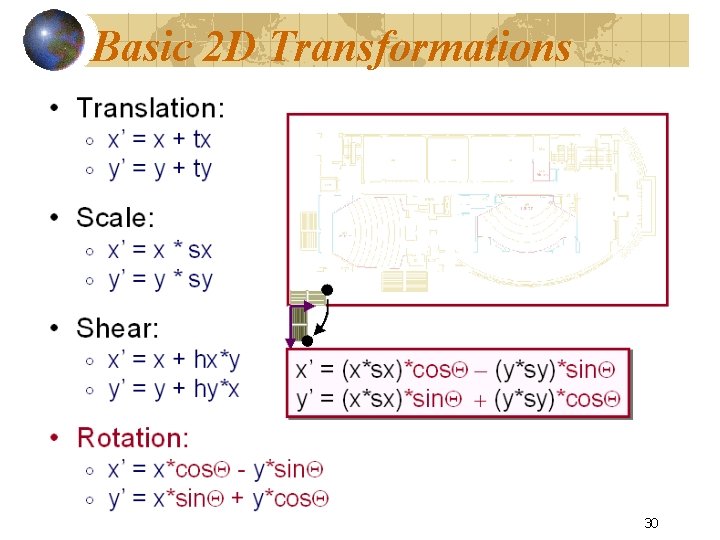
Basic 2 D Transformations 30

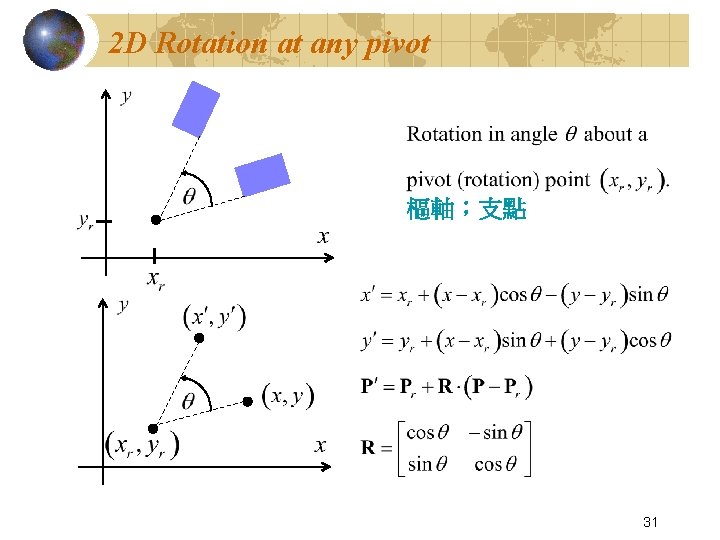
2 D Rotation at any pivot 樞軸；支點 31

Basic 2 D Transformations 32

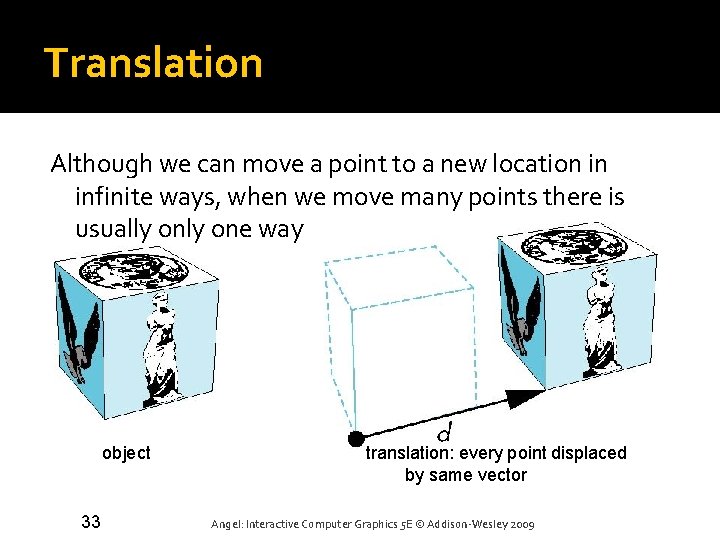
Translation Although we can move a point to a new location in infinite ways, when we move many points there is usually one way object 33 translation: every point displaced by same vector Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

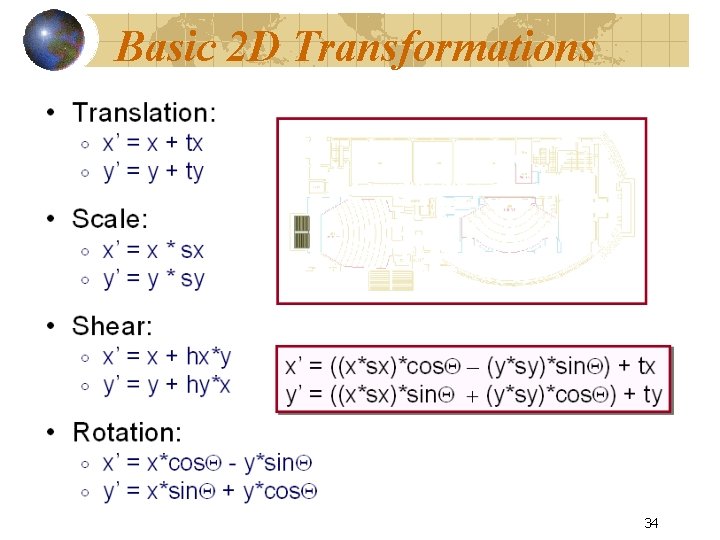
Basic 2 D Transformations 34

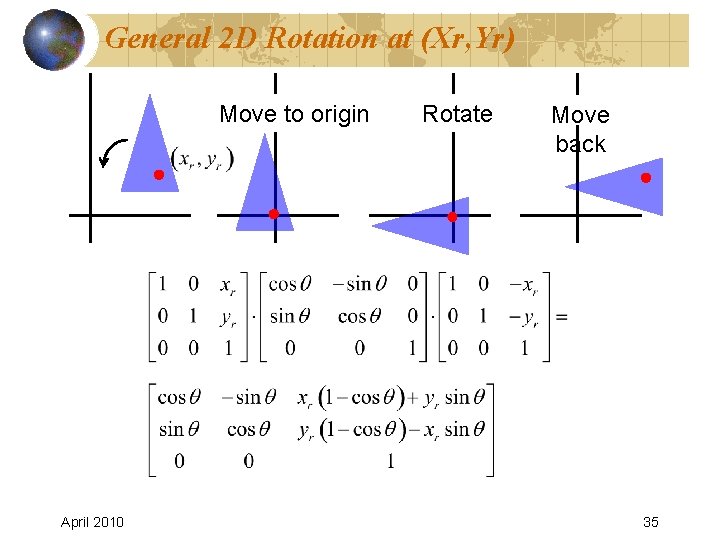
General 2 D Rotation at (Xr, Yr) Move to origin April 2010 Rotate Move back 35

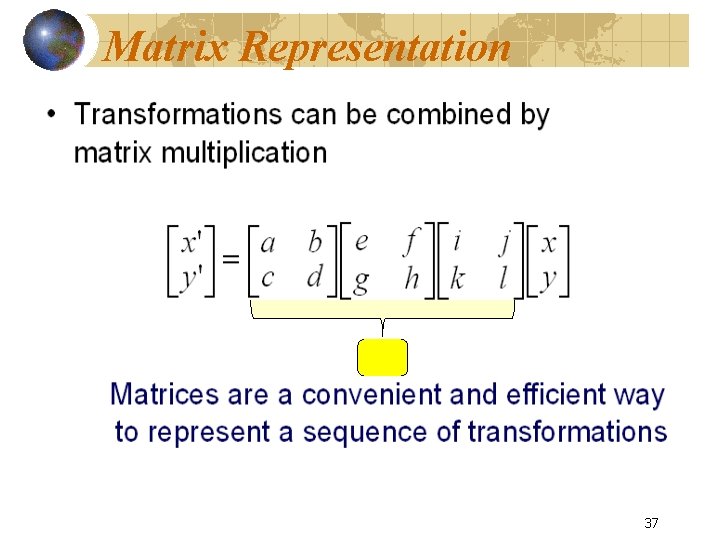
Matrix Representation 36

Matrix Representation 37

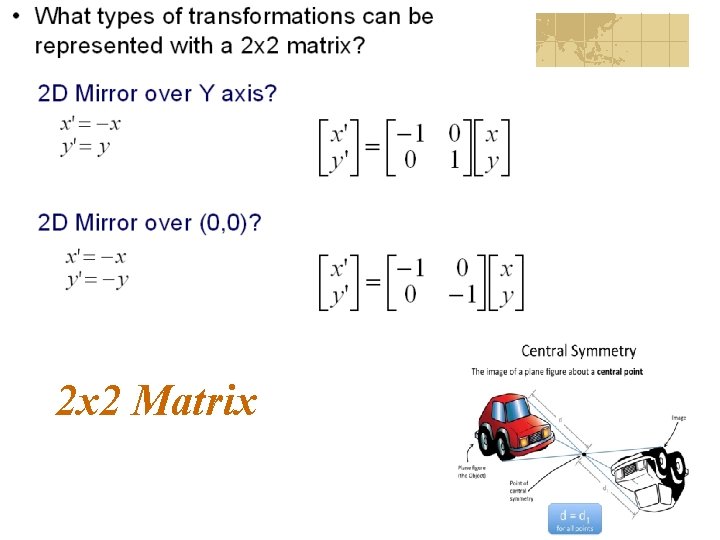
2 x 2 Matrix 38

2 x 2 Matrix 39

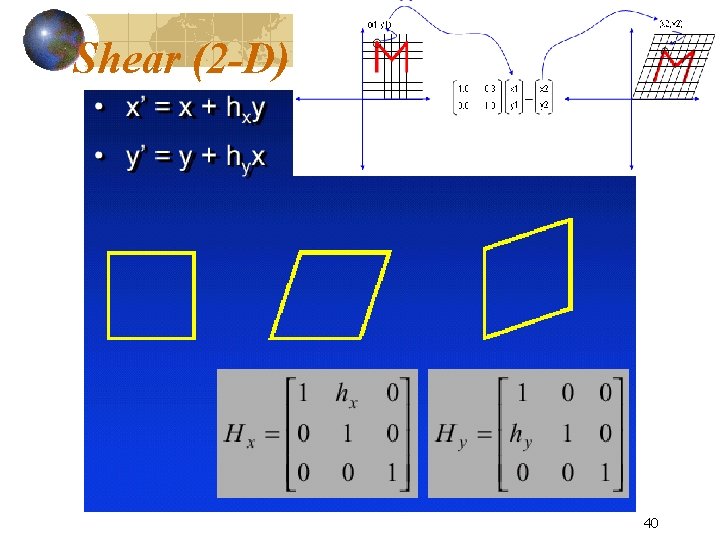
Shear (2 -D) 40

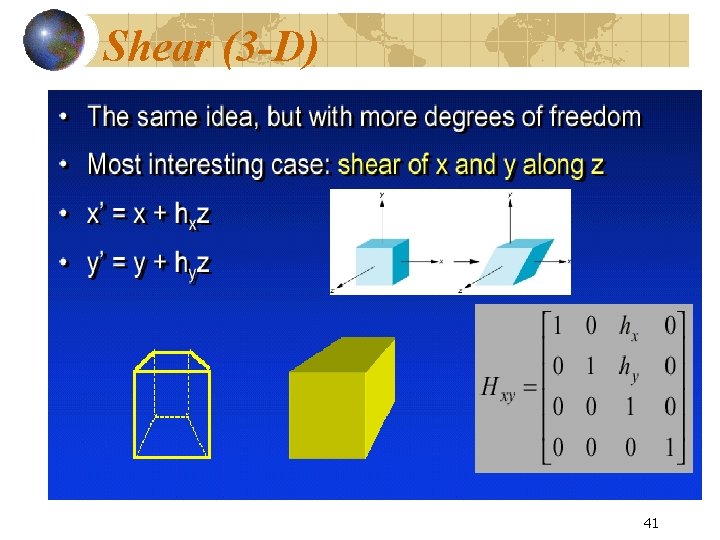
Shear (3 -D) 41

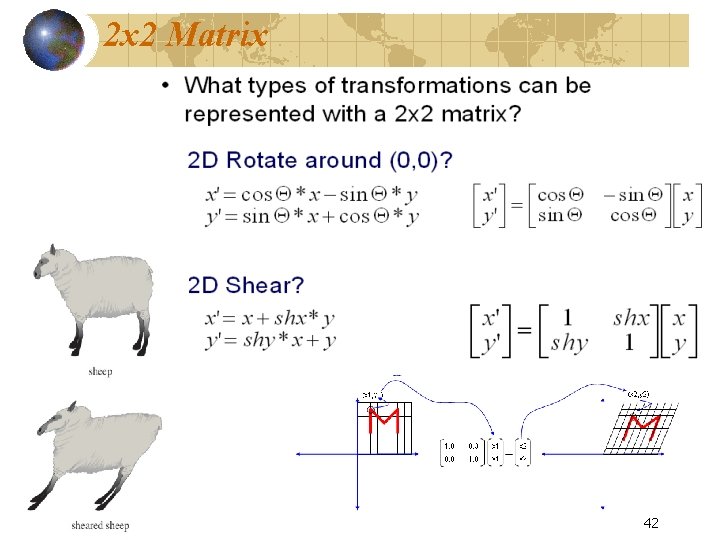
2 x 2 Matrix 42

2 x 2 Matrix 43

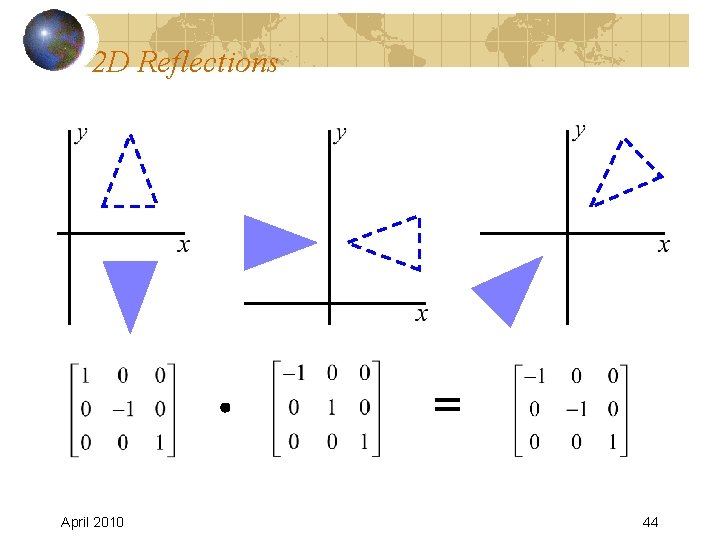
2 D Reflections April 2010 44

2 x 2 Matrix 45

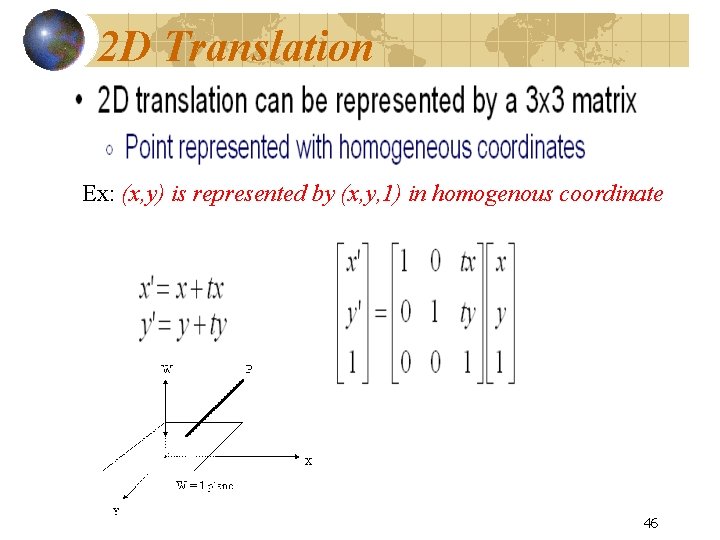
2 D Translation Ex: (x, y) is represented by (x, y, 1) in homogenous coordinate 46

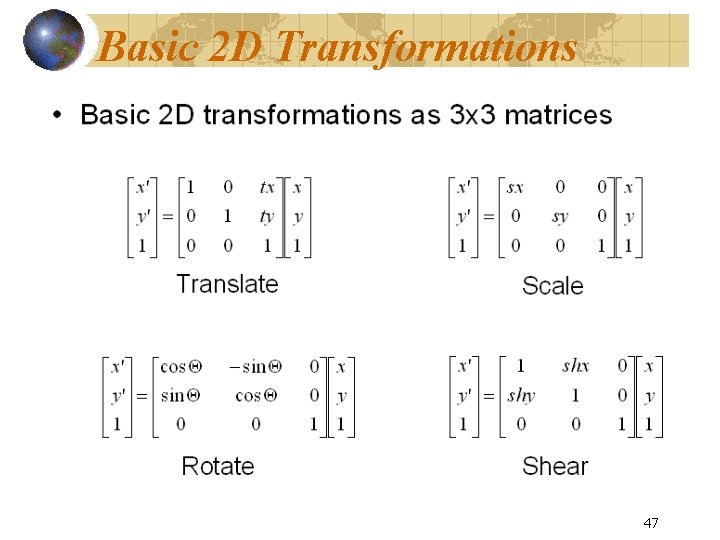
Basic 2 D Transformations 47

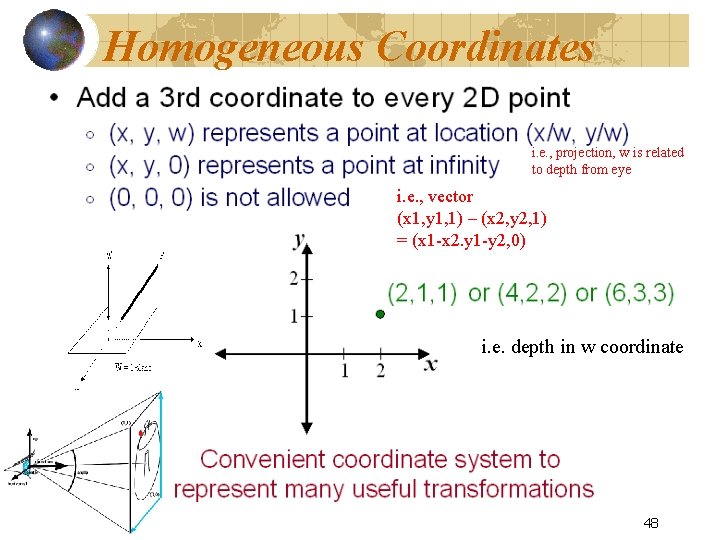
Homogeneous Coordinates i. e. , projection, w is related to depth from eye i. e. , vector (x 1, y 1, 1) – (x 2, y 2, 1) = (x 1 -x 2. y 1 -y 2, 0) i. e. depth in w coordinate 48

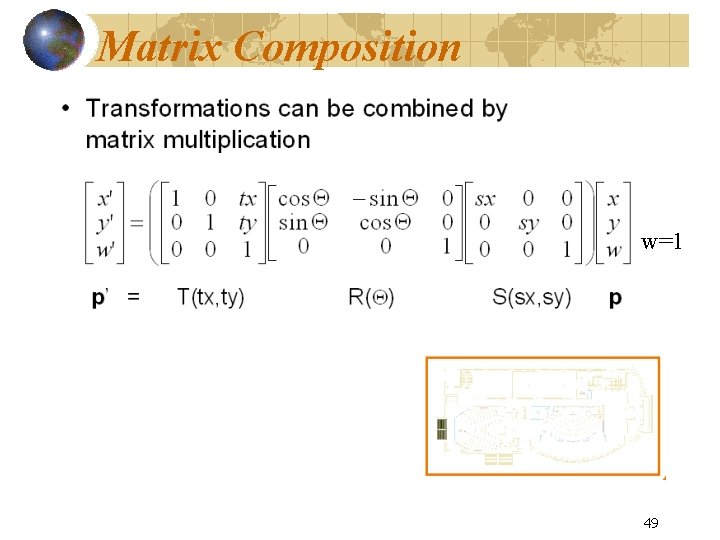
Matrix Composition w=1 49

Matrix Composition i. e. 1 point is OK i. e. if many points are used, matries are composed first 50

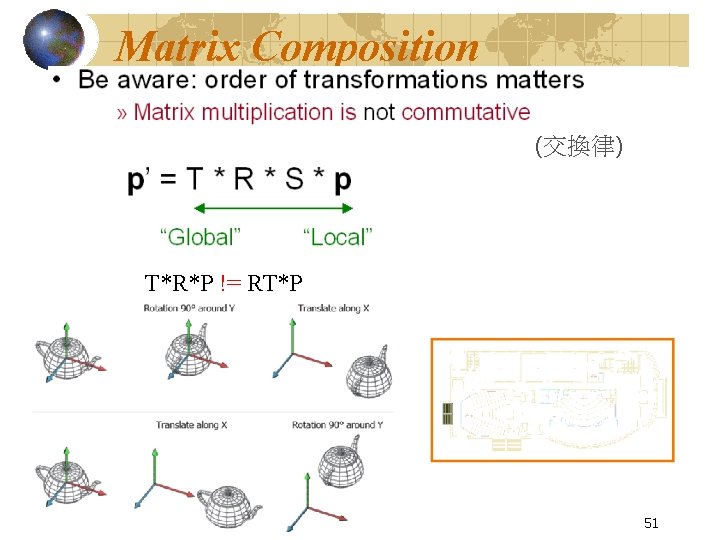
Matrix Composition (交換律) T*R*P != RT*P 51

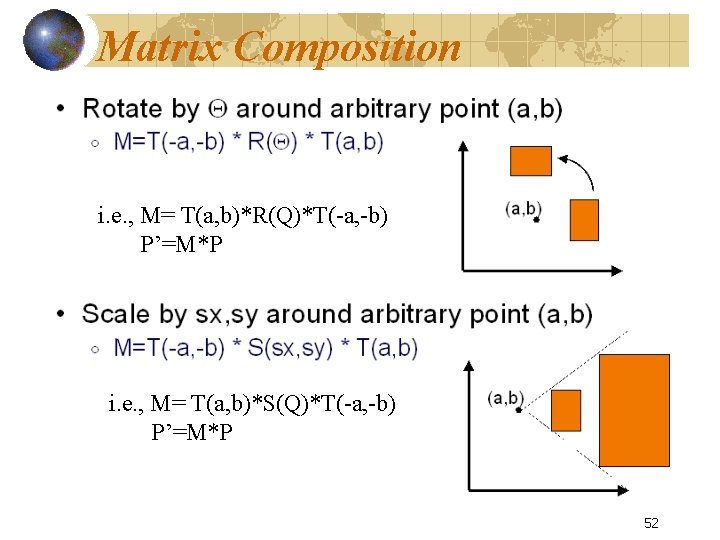
Matrix Composition i. e. , M= T(a, b)*R(Q)*T(-a, -b) P’=M*P i. e. , M= T(a, b)*S(Q)*T(-a, -b) P’=M*P 52

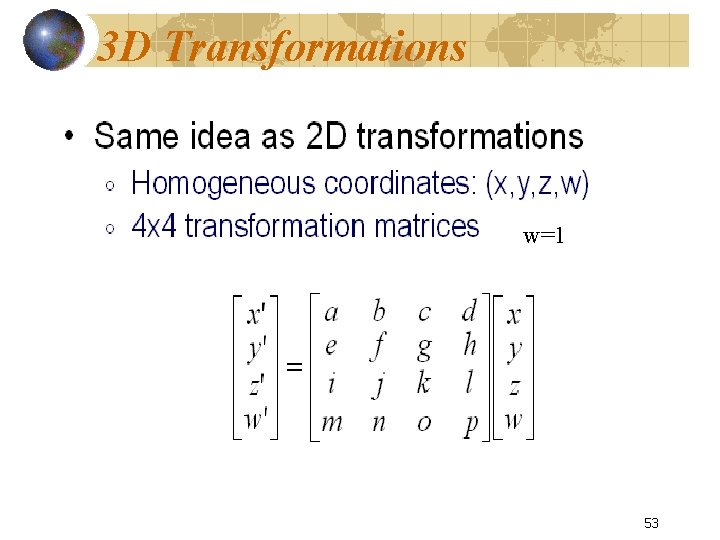
3 D Transformations w=1 53

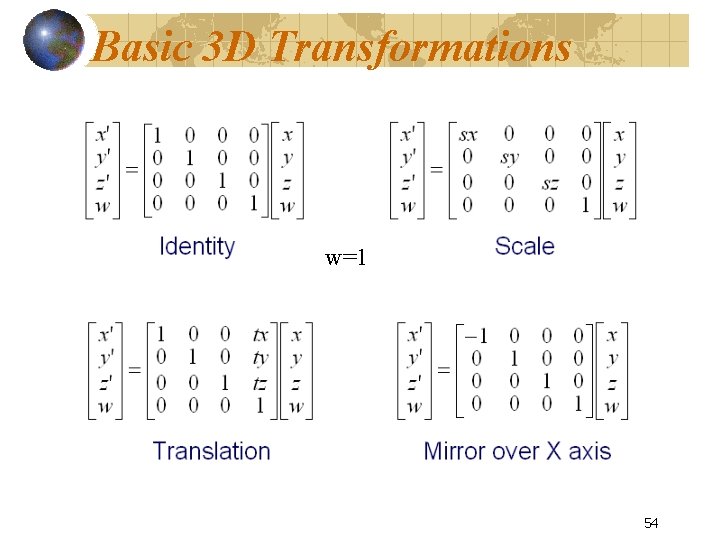
Basic 3 D Transformations w=1 54

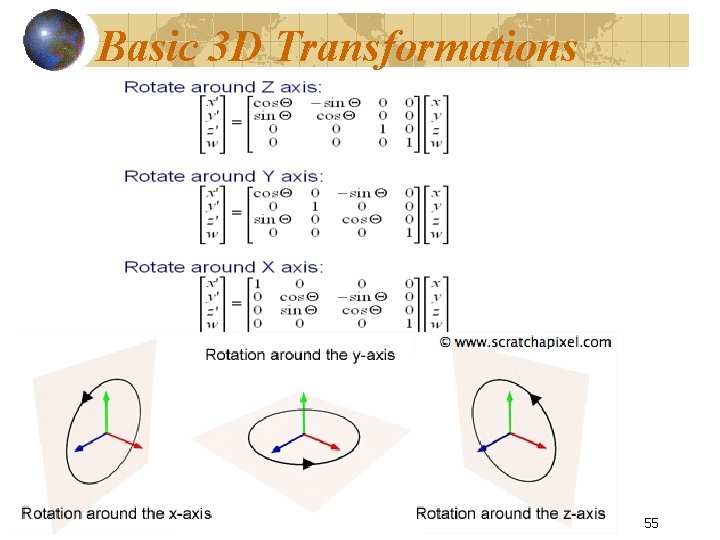
Basic 3 D Transformations 55

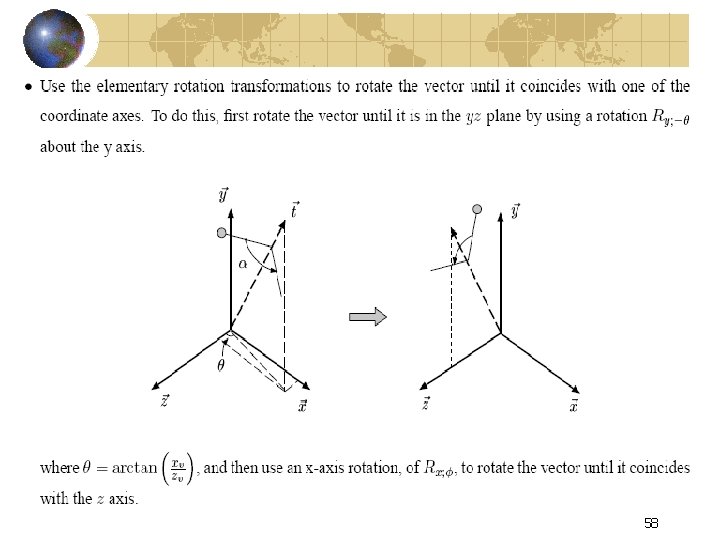
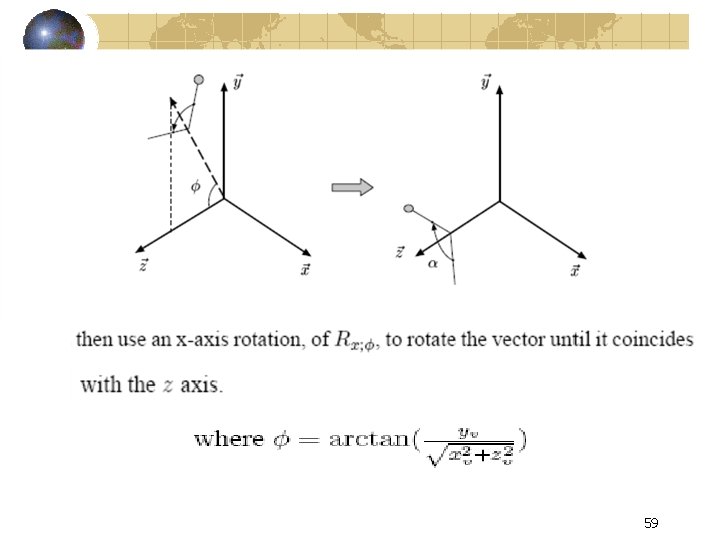
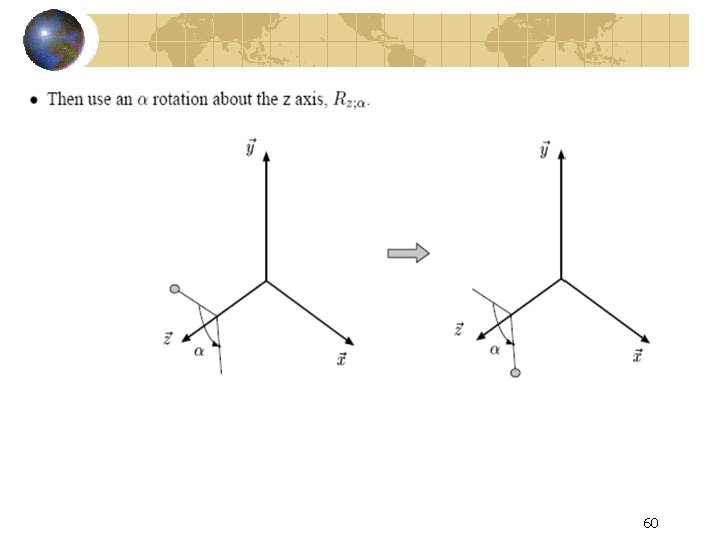
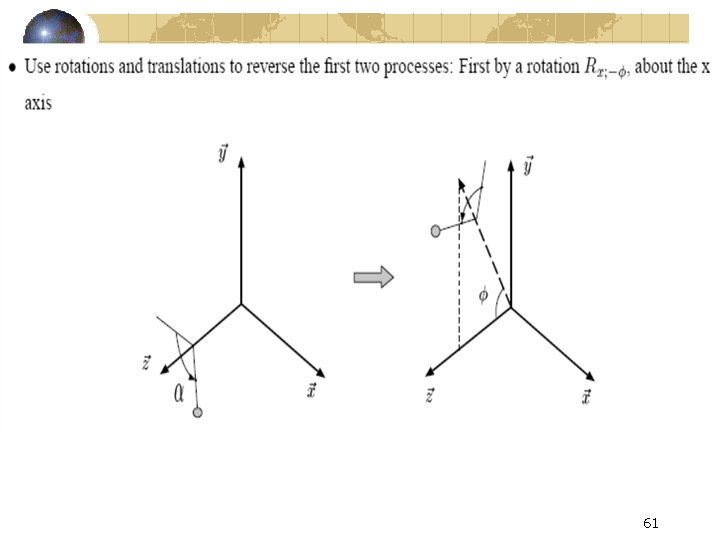
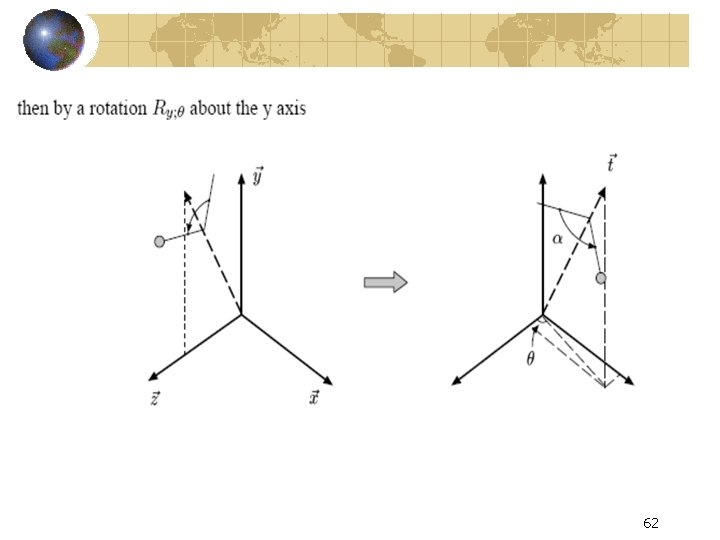
General rotation about an axis 56

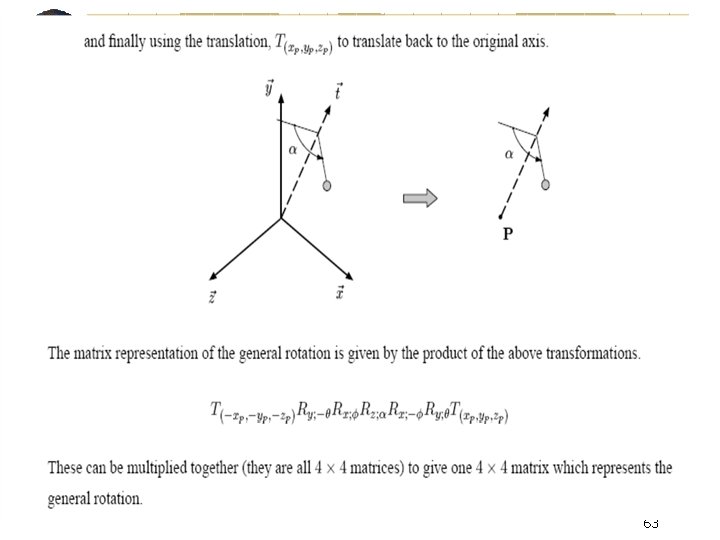
Developing the General Rotation Matrix → t= <Xv, Yv, Zv> 57

58

59

60

61

62

63

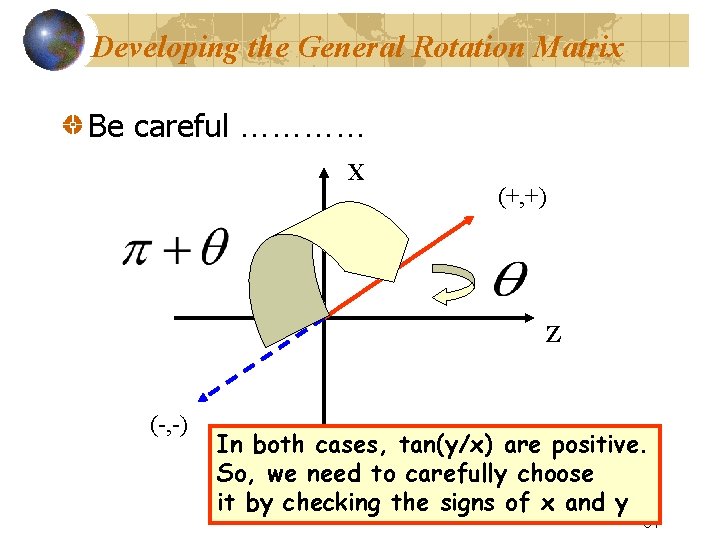
Developing the General Rotation Matrix Be careful ………… X (+, +) Z (-, -) In both cases, tan(y/x) are positive. So, we need to carefully choose it by checking the signs of x and y 64

Open. GL transformation Matrices 65

Example -1 planet. c Control: • • • ‘d’ ‘y’ ‘a’ ‘A’ ESC 66

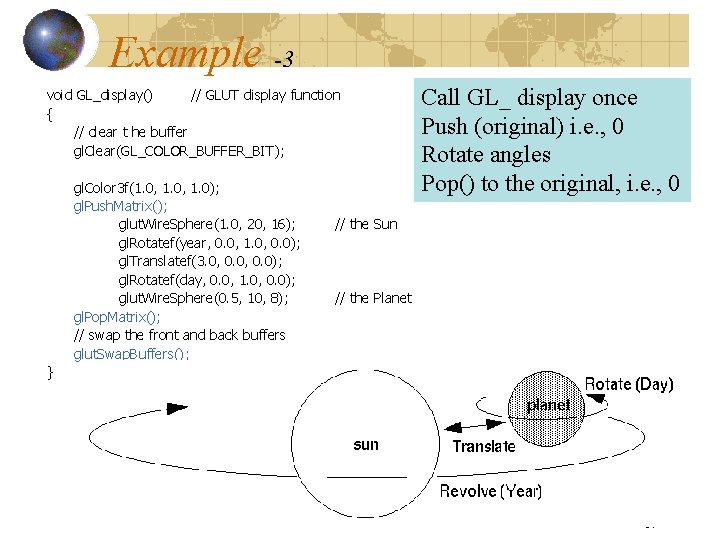
Example -3 void GL_display() // GLUT display function { // clear t he buffer gl. Clear(GL_COLOR_BUFFER_BIT); gl. Color 3 f(1. 0, 1. 0); gl. Push. Matrix(); glut. Wire. Sphere(1. 0, 20, 16); gl. Rotatef(year, 0. 0, 1. 0, 0. 0); gl. Translatef(3. 0, 0. 0); gl. Rotatef(day, 0. 0, 1. 0, 0. 0); glut. Wire. Sphere(0. 5, 10, 8); gl. Pop. Matrix(); // swap the front and back buffers glut. Swap. Buffers(); Call GL_ display once Push (original) i. e. , 0 Rotate angles Pop() to the original, i. e. , 0 // the Sun // the Planet } 67

Example -4 void GL_idle() // GLUT idle function { day += 10. 0; if(day > 360. 0) day -= 360. 0; year += 1. 0; if(year > 360. 0) year -= 360. 0; (i. e. , planet self-rotation +10 degrees, faster) (i. e. , planet rotate sun + 1 degree, slower) // recall GL_display() function glut. Post. Redisplay(); (i. e. , call run display function) } 68

Example -5 void GL_keyboard(unsigned char key, int x, int y) // GLUT keyboard function { switch(key) { case 'd': day += 10. 0; if(day > 360. 0) day -= 360. 0; glut. Post. Redisplay(); break; case 'y': year += 1. 0; if(year > 360. 0) year -= 360. 0; glut. Post. Redisplay(); break; case 'a': glut. Idle. Func(GL_idle); // assign idle function break; case 'A': glut. Idle. Func(0); break; case 27: exit(0); } } 69

Example -6 int main(int argc, char** argv) { glut. Init(&argc, argv); glut. Init. Window. Size(500, 500); glut. Init. Window. Position(0, 0); glut. Init. Display. Mode(GLUT_DOUBLE | GLUT_RGB); glut. Create. Window("Planet"); init(); glut. Display. Func(GL_display); glut. Reshape. Func(GL_reshape); glut. Keyboard. Func(GL_keyboard); glut. Main. Loop(); return 0; } 70

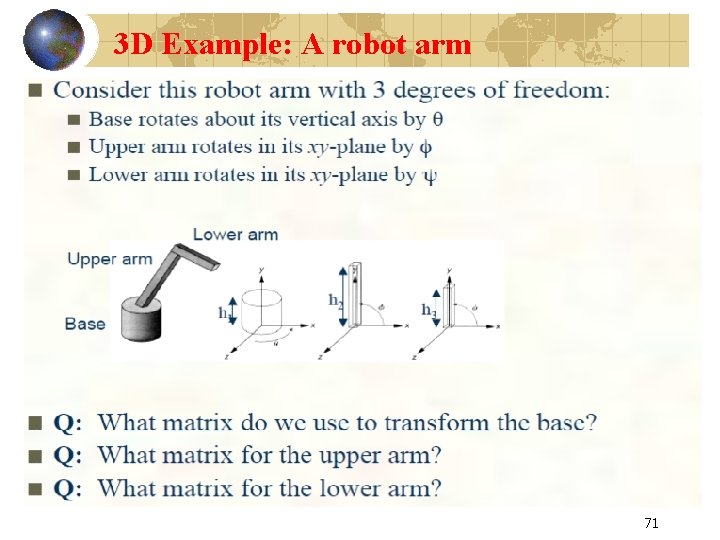
3 D Example: A robot arm 71

72

Open. GL better implementation 73

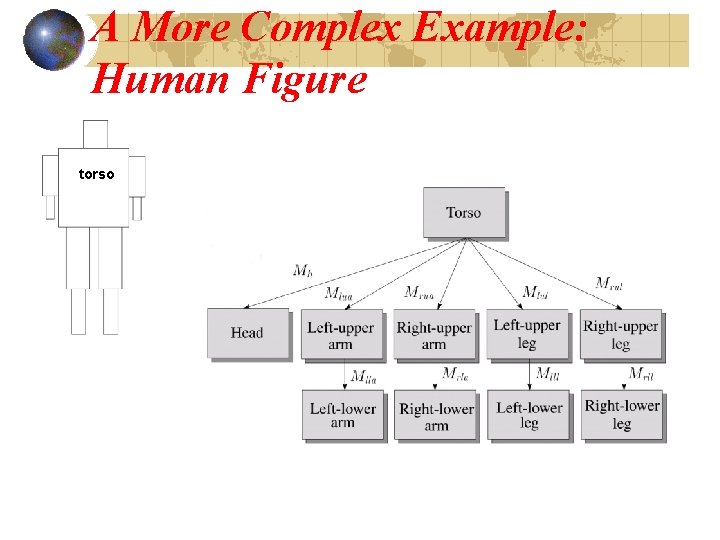
A More Complex Example: Human Figure torso

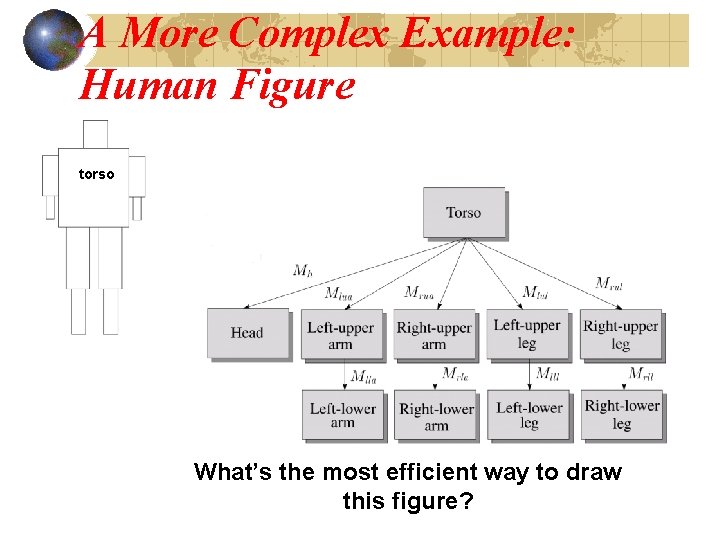
A More Complex Example: Human Figure torso What’s the most efficient way to draw this figure?

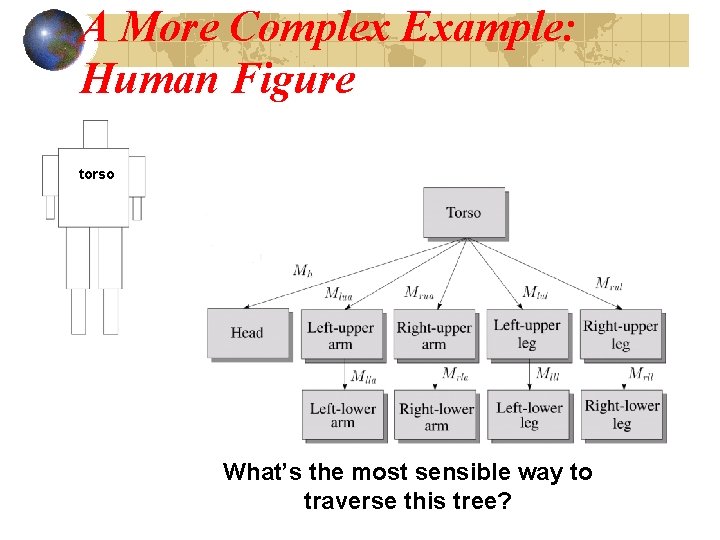
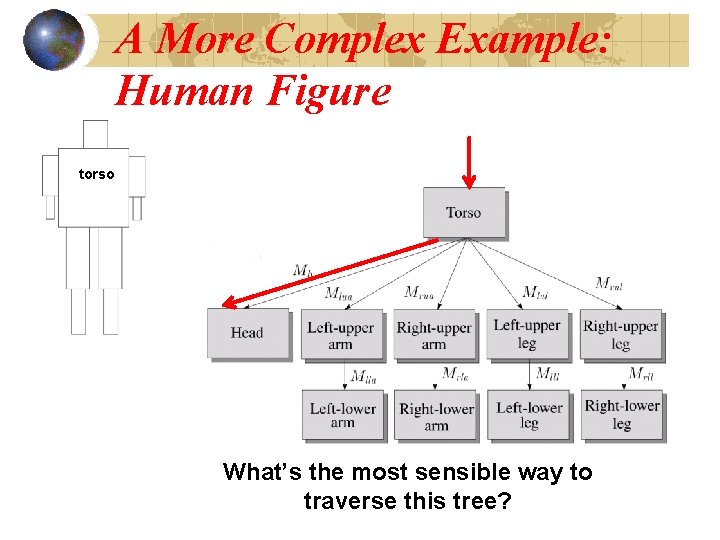
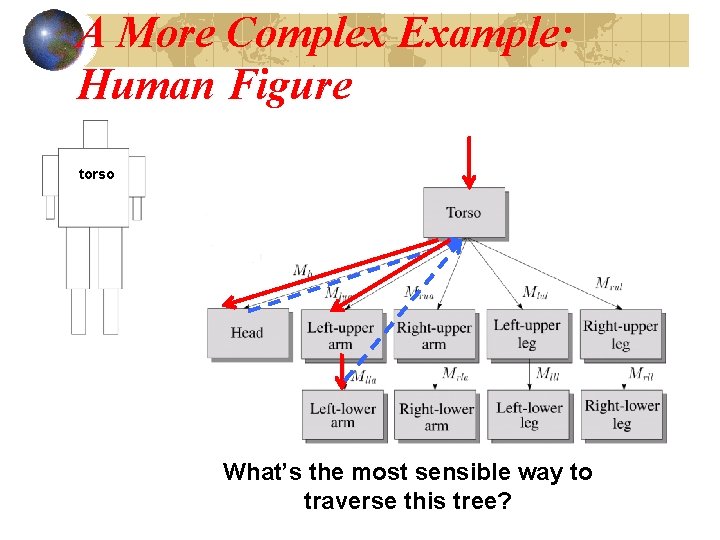
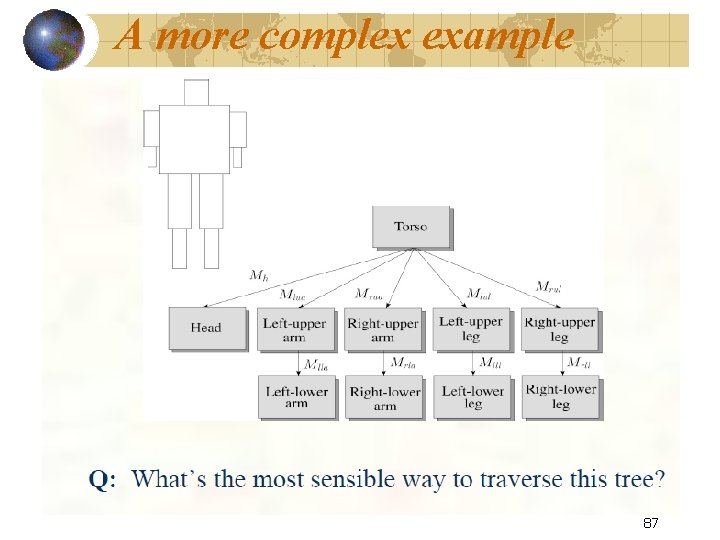
A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

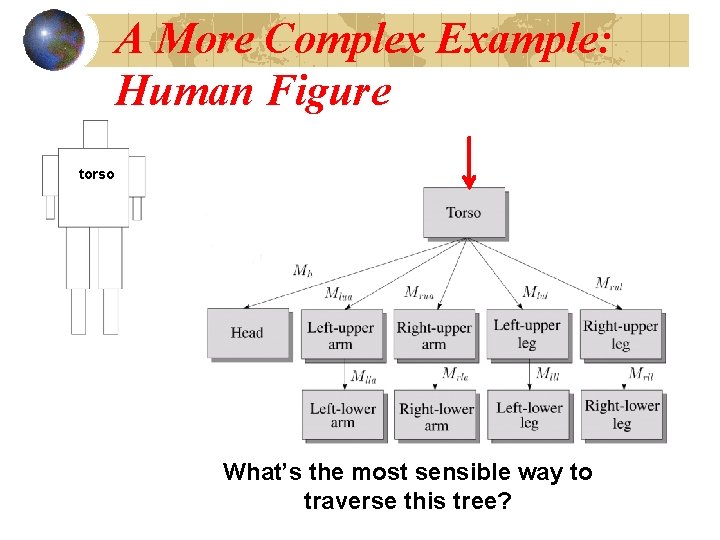
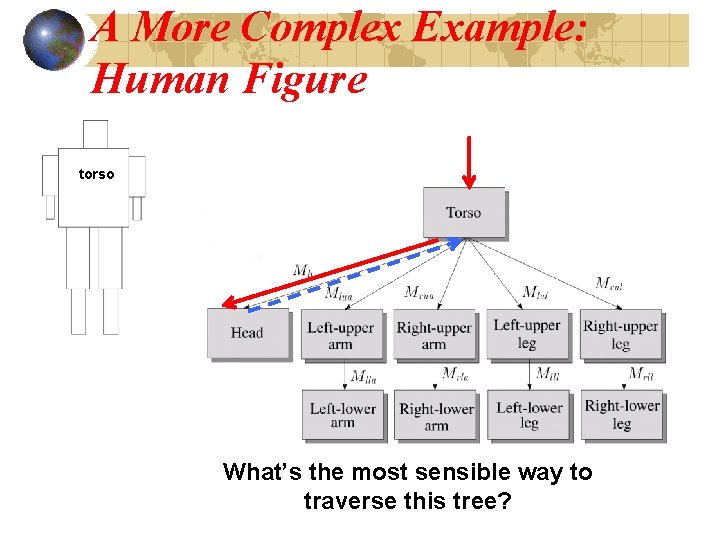
A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

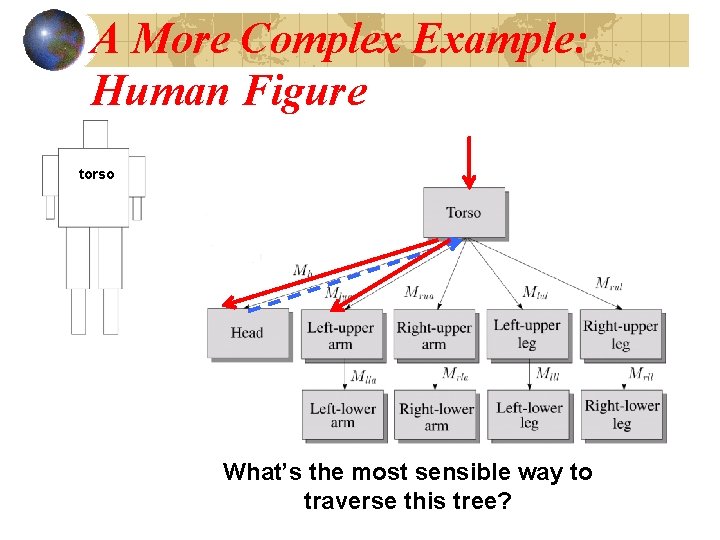
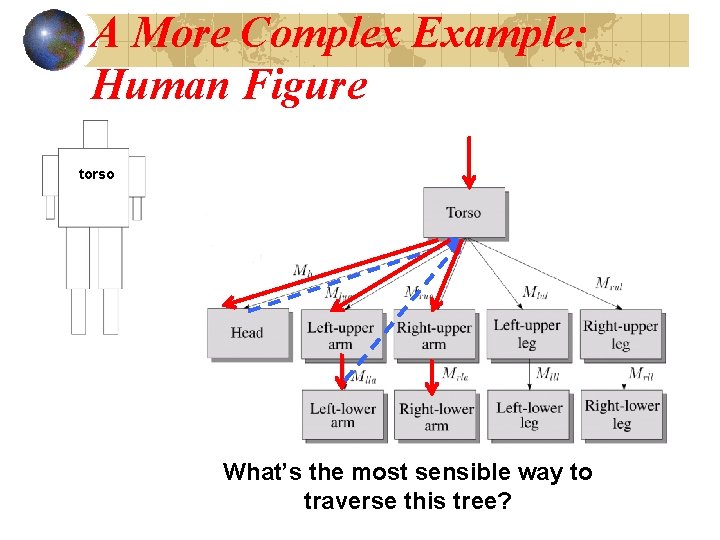
A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

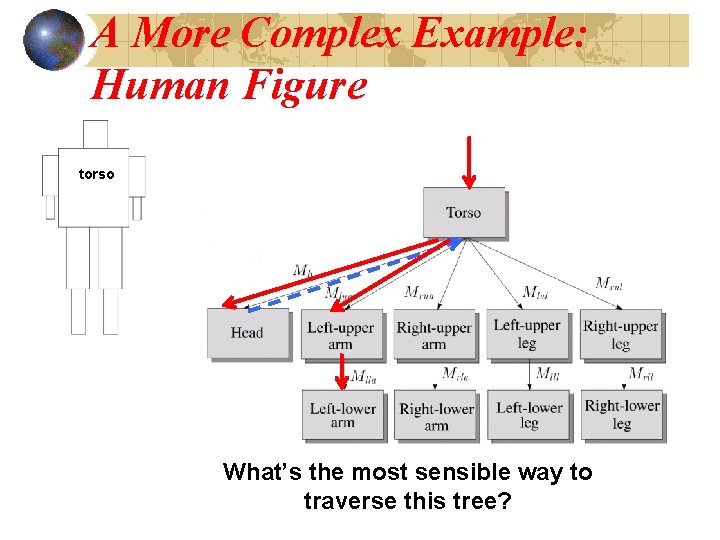
A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

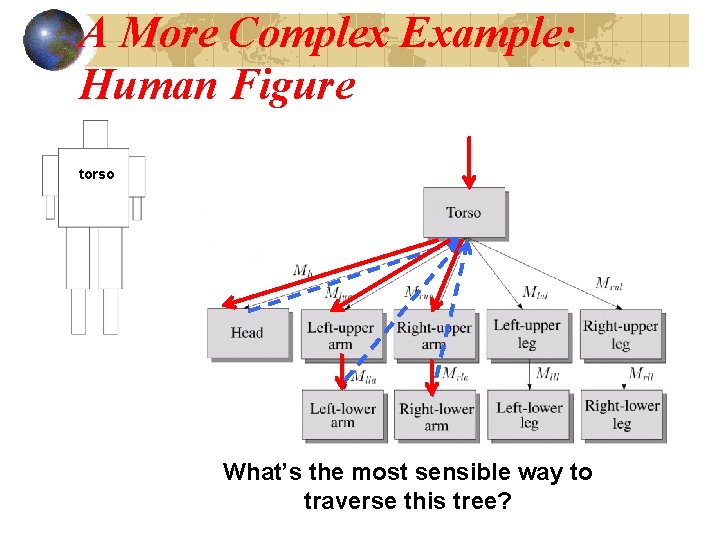
A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

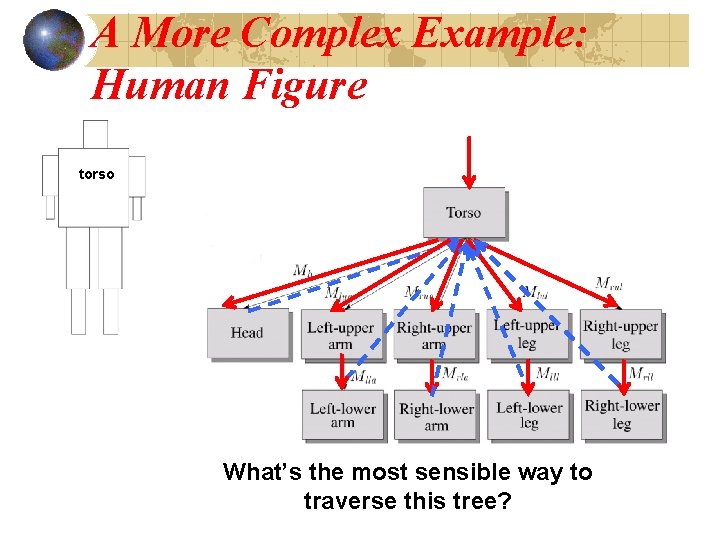
A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

A More Complex Example: Human Figure torso What’s the most sensible way to traverse this tree?

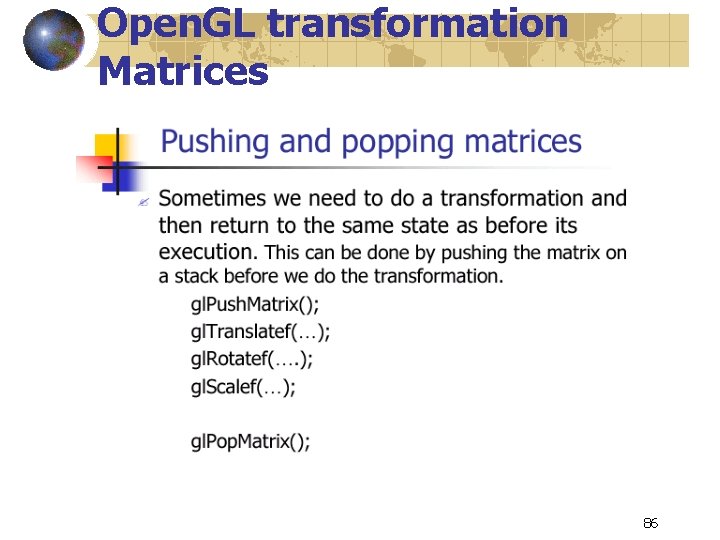
Open. GL transformation Matrices 86

A more complex example 87

88

n p 0 t 2 t 1 p 2 p 1 89

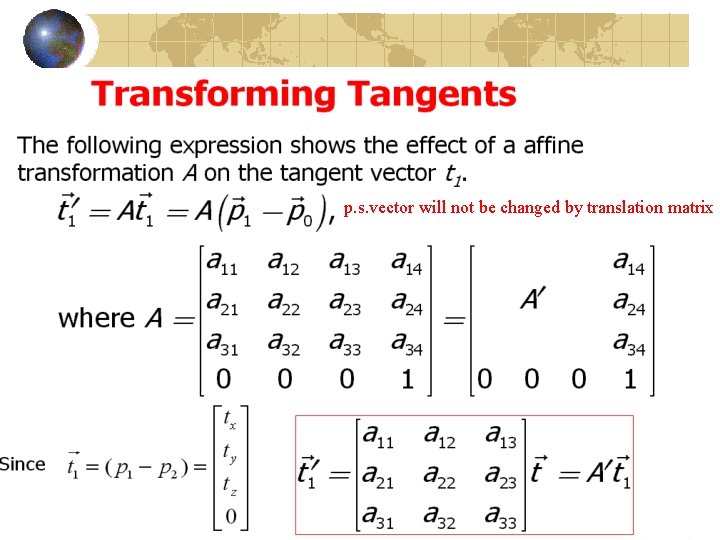
p. s. vector will not be changed by translation matrix 90

91

Inverse Transformation 92

Open. GL transformation Matrices 93

94

95

96

97

98

99

100

101

102

103

104