Geometrical Construction To bisect a line To divide

Geometrical Construction • To bisect a line • To divide a line into a number of equal parts • To divide a line in a given proportion • To bisect an angle • To find the center of an arc • To inscribe a circle in a triangle. • To draw the circumscribing circle of a triangle.

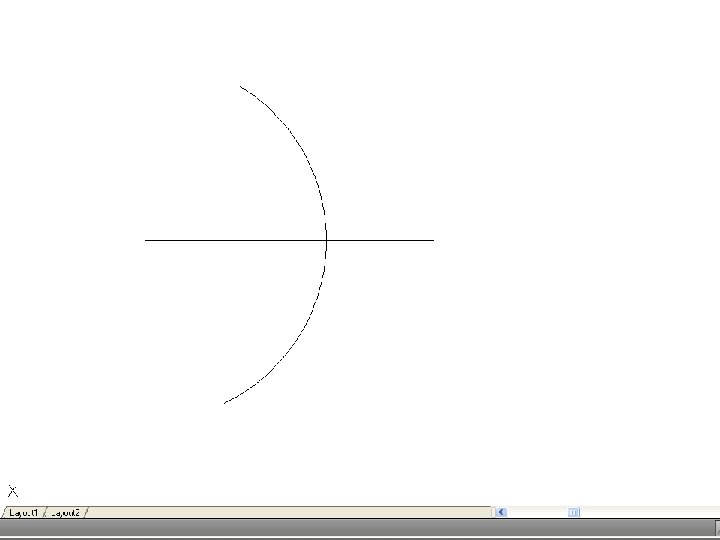
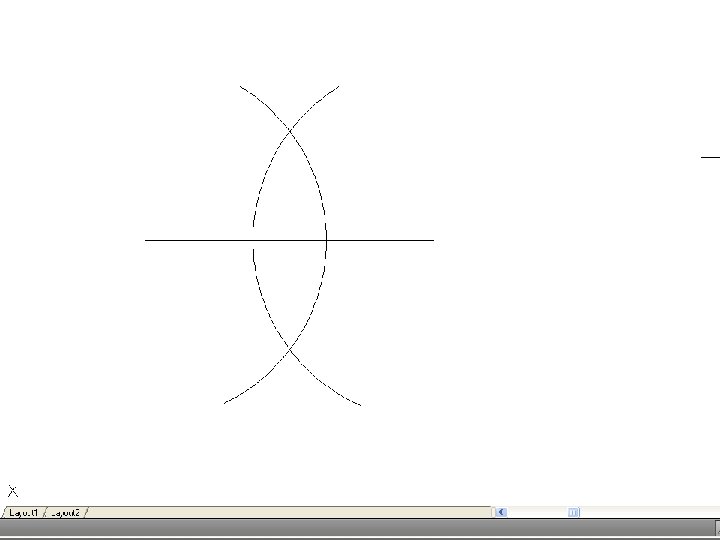
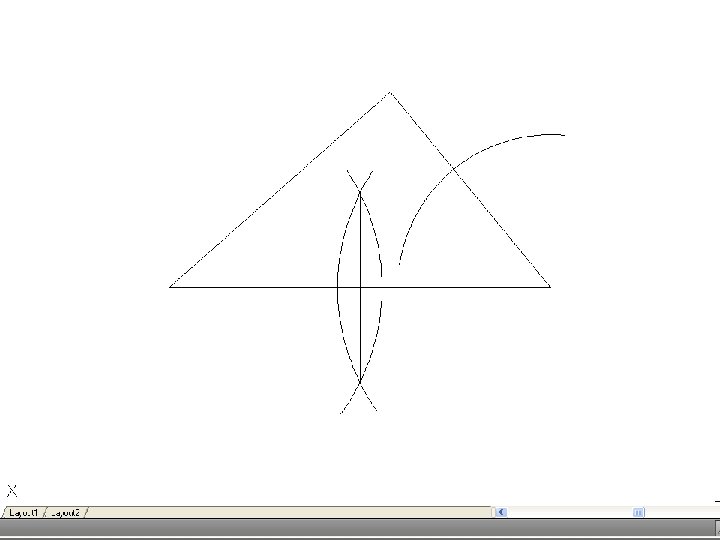
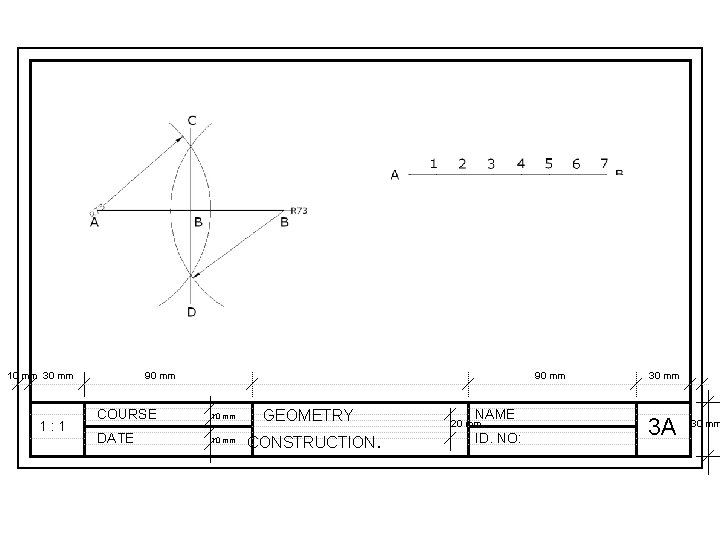
• To bisect a line – Draw the given line AB, with centers A and B and radius R greater than half of AB, draw arcs to intersect a t C and D. Join CD, when E will be the mid point of the line. Also CD will be perpendicular to AB

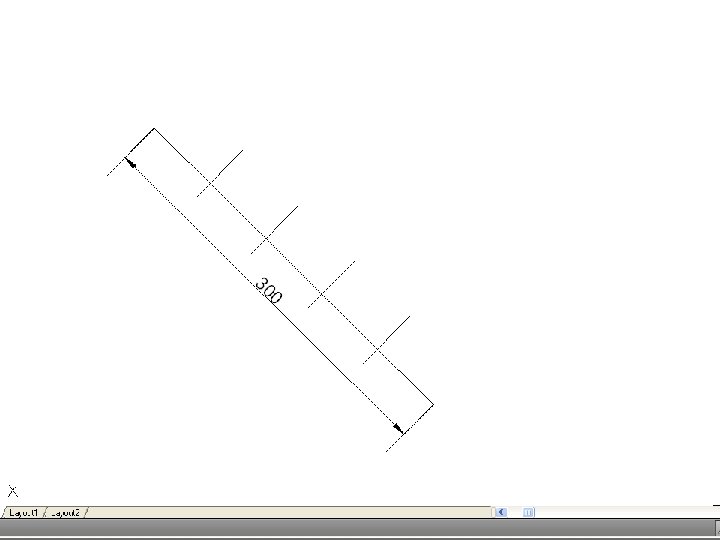
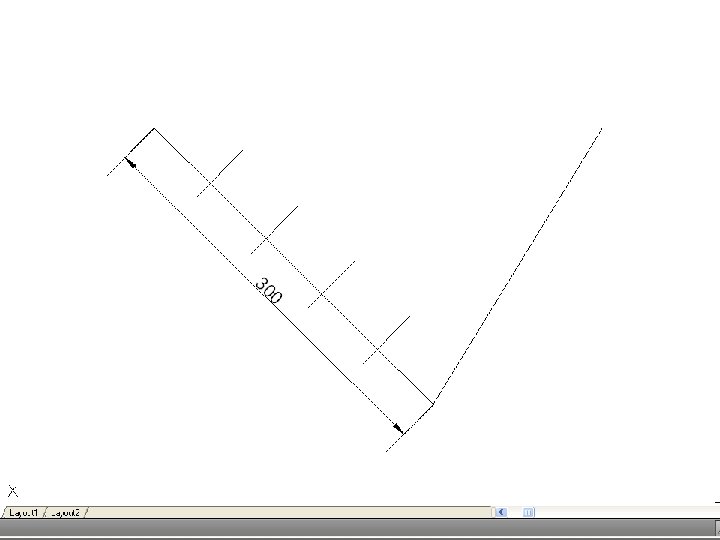
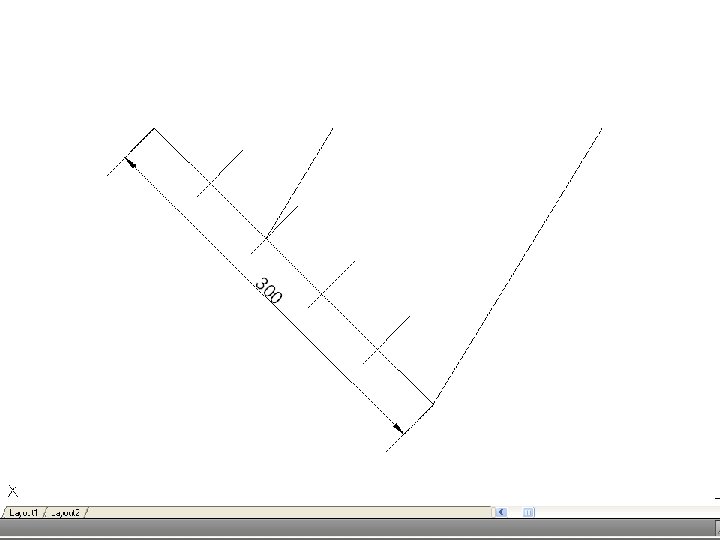
• To divide a line into a number of equal parts – From one end of the given line (say A), draw AC at any convenient angle. Using dividers or a scale, mark off from A on AC the required number of equal parts, making them of any suitable length. Join the last point to B on the given line, and through the other points draw parallels to this line to cut the given line. This construction makes use of the properties of similar triangles.

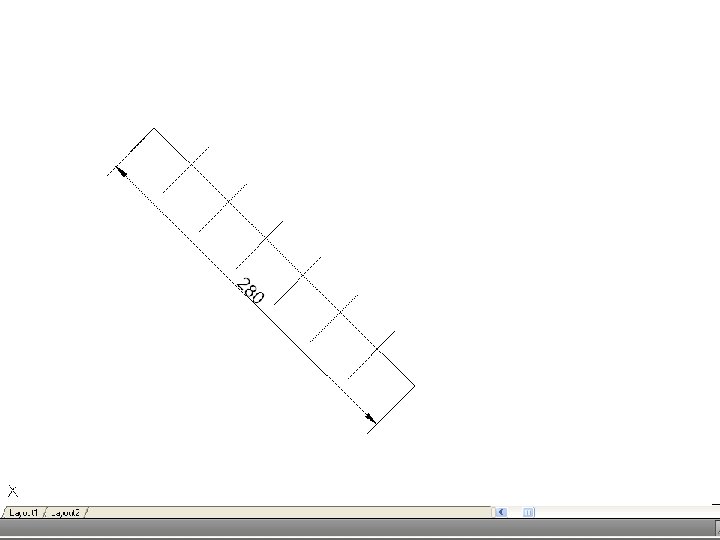
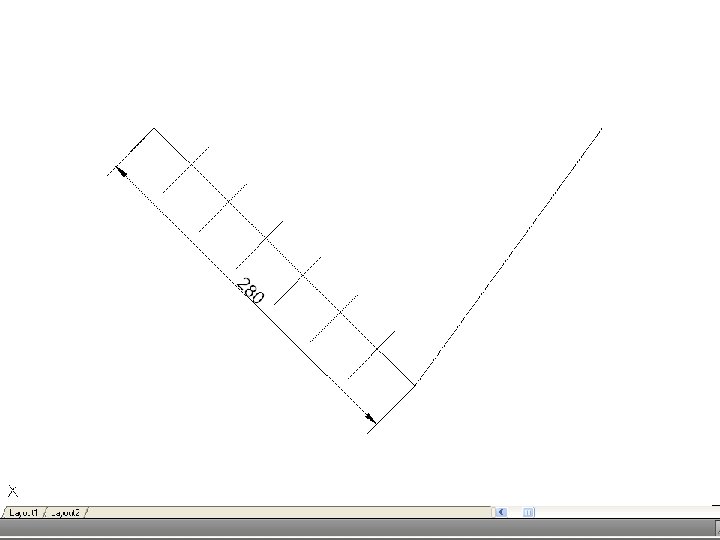
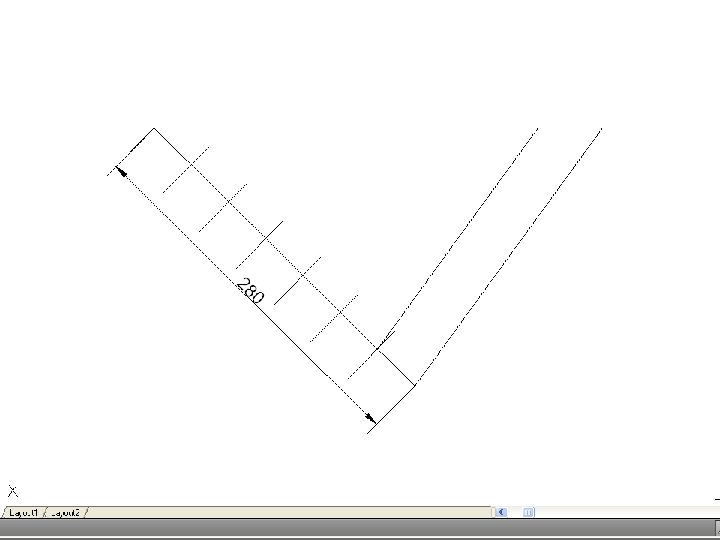
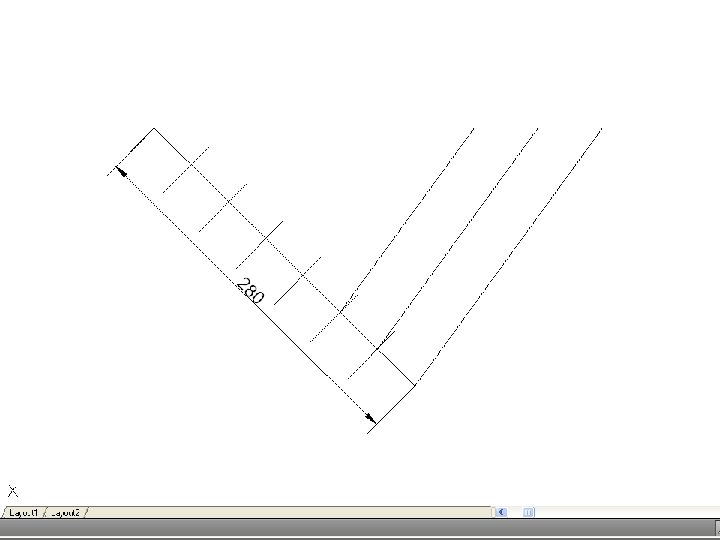
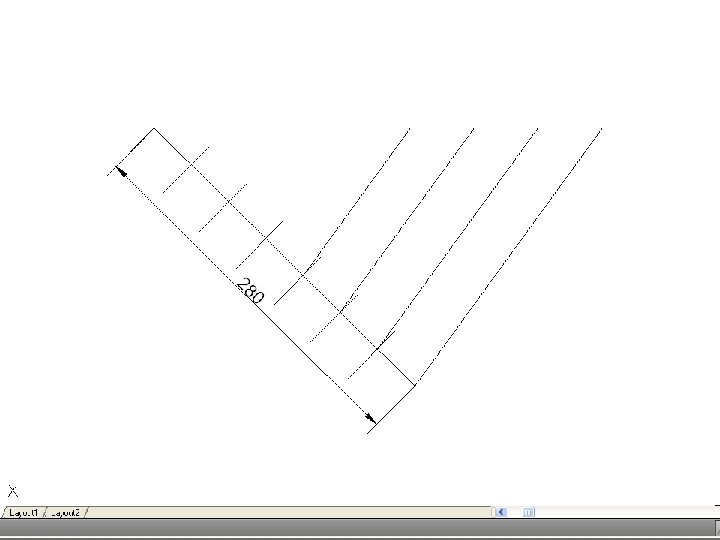
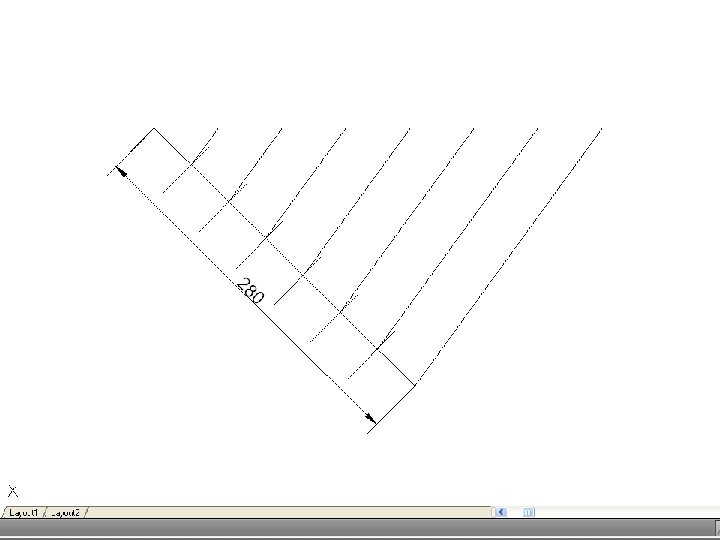
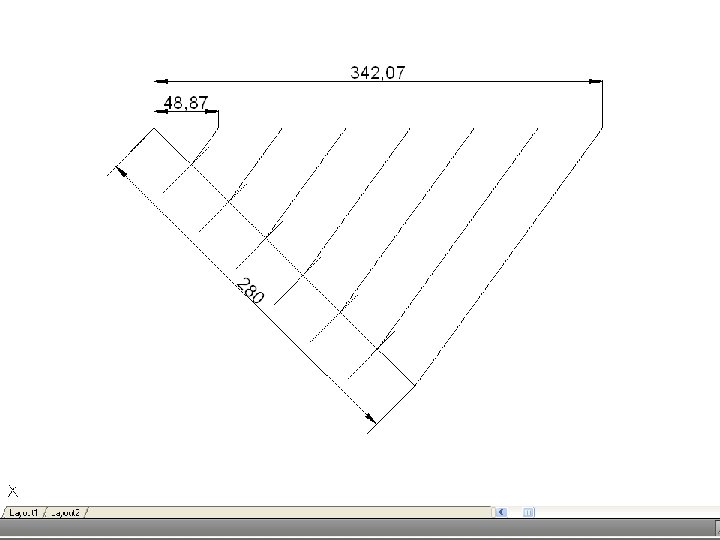
• To divide a line in a given proportion – Suppose the proportion to be 2 : 3. using the previous construction, proceed as if to divide the line into 5 parts (2 plus 3) but only draw a line through point 2 on AD. Then AB will be divided in the required proportion.

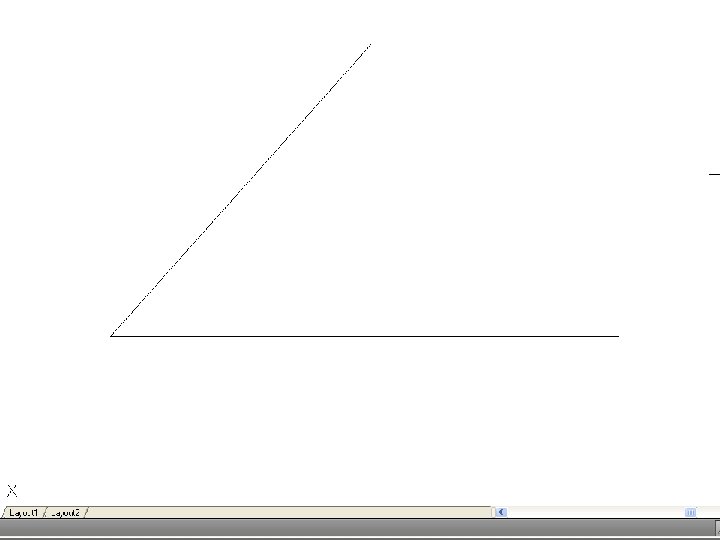
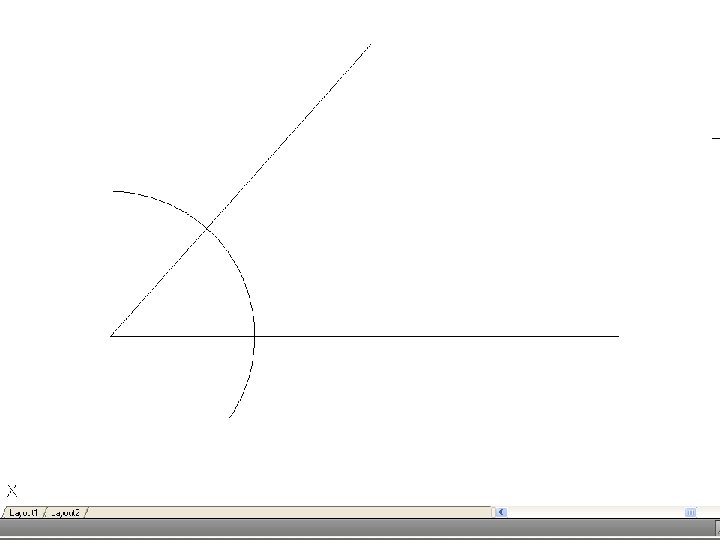
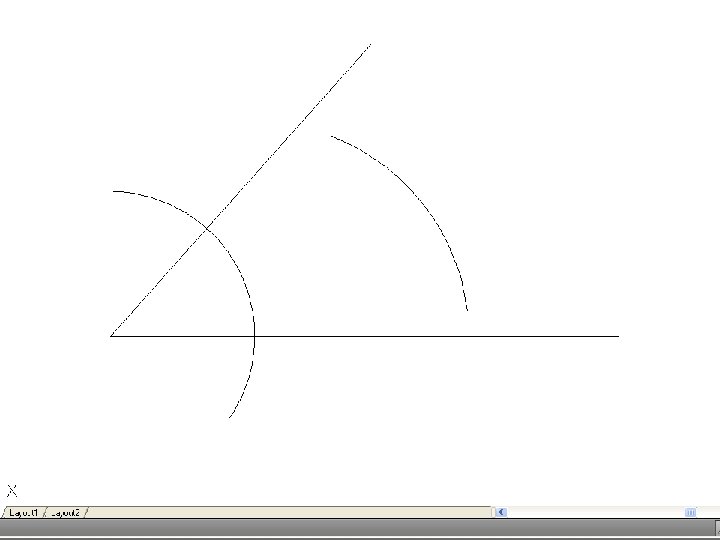
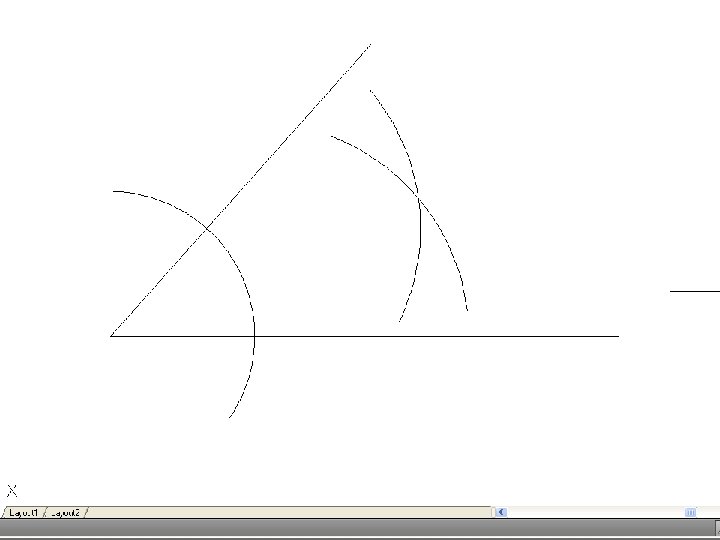
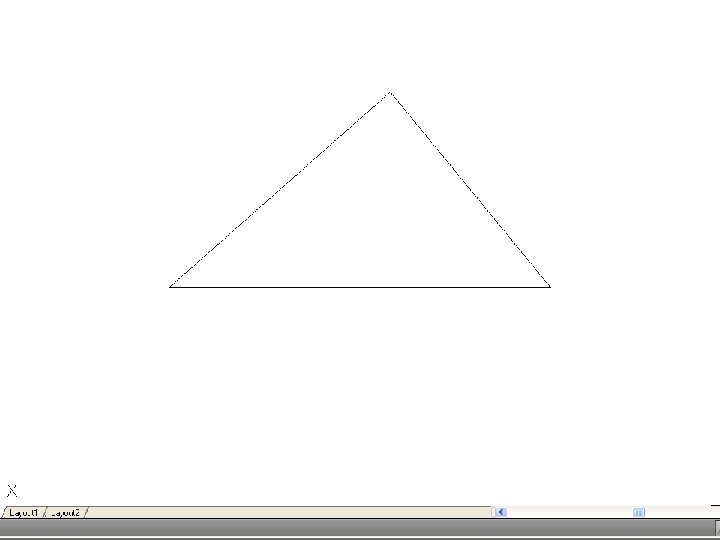
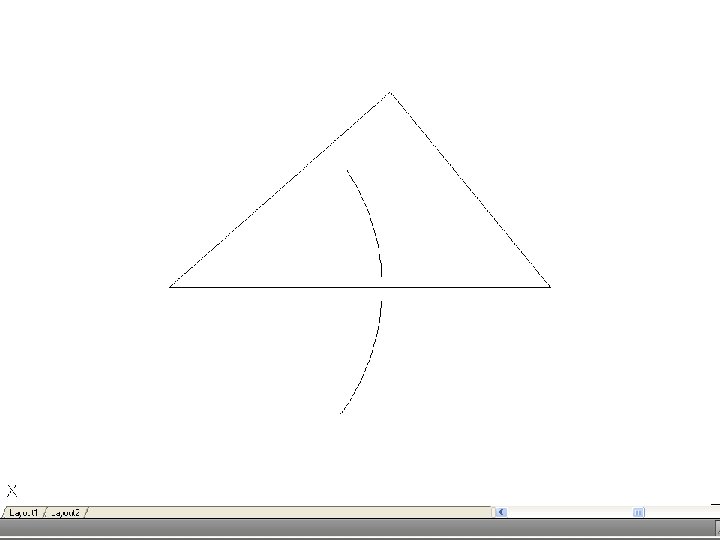
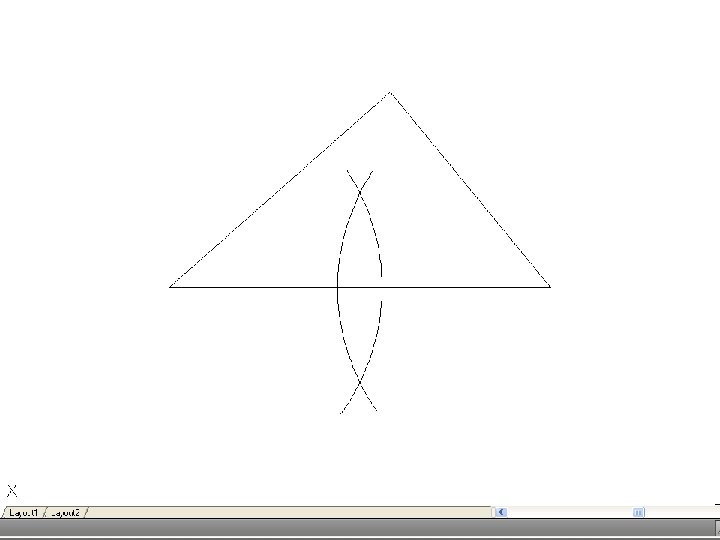
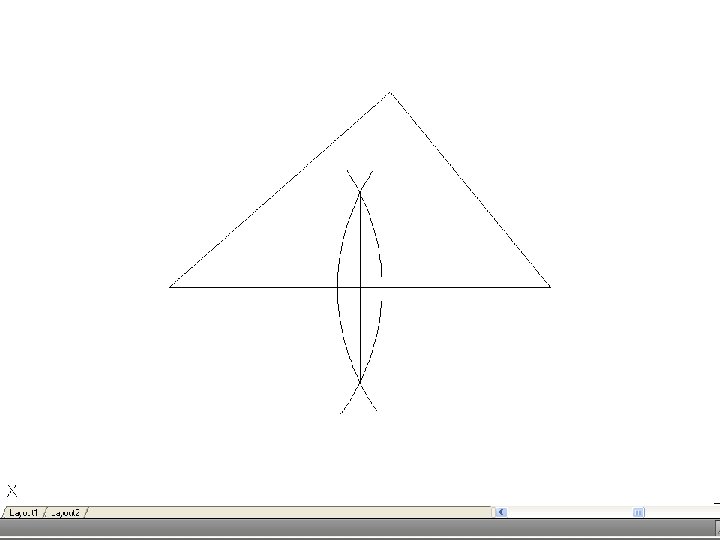
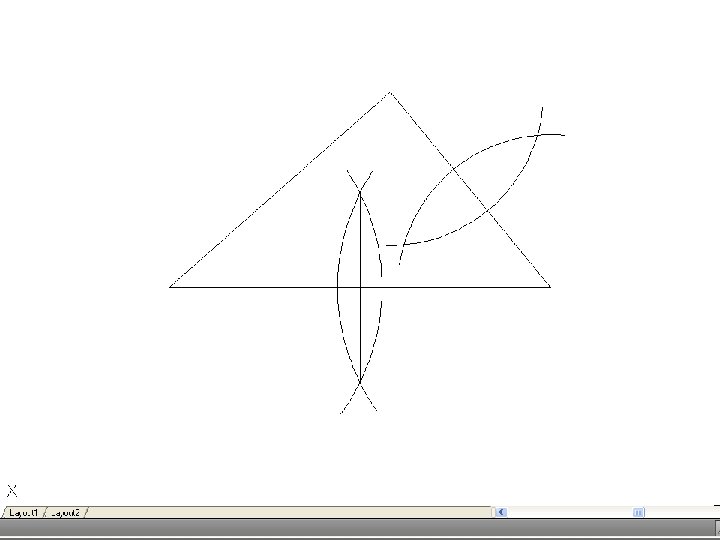
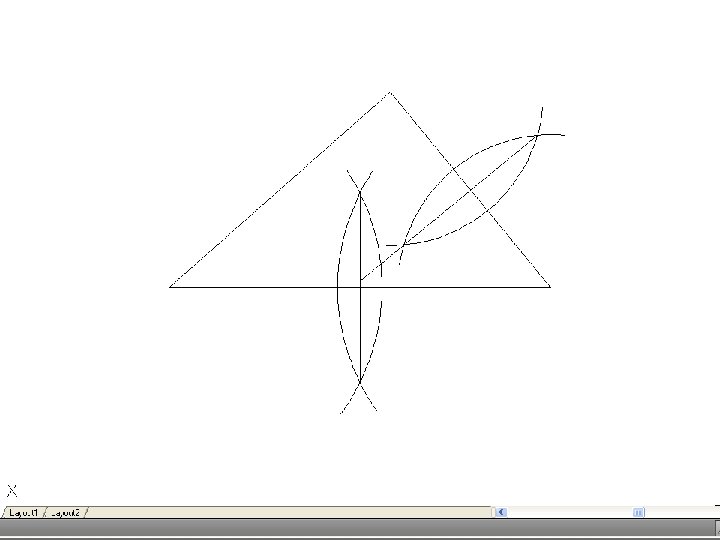
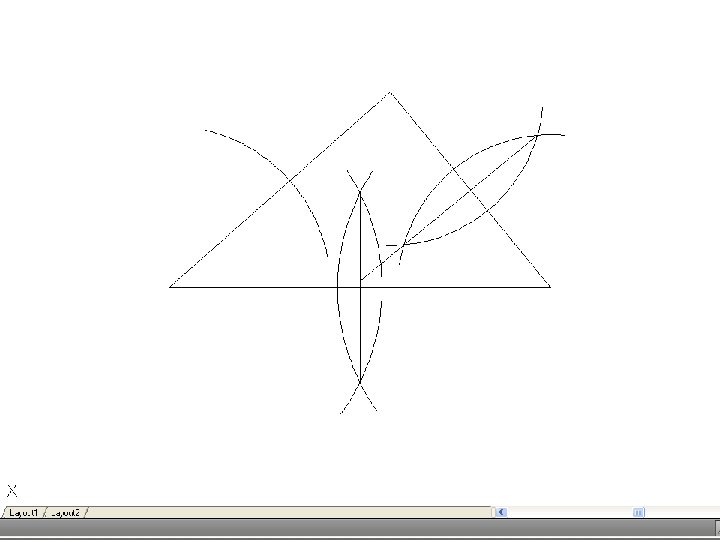
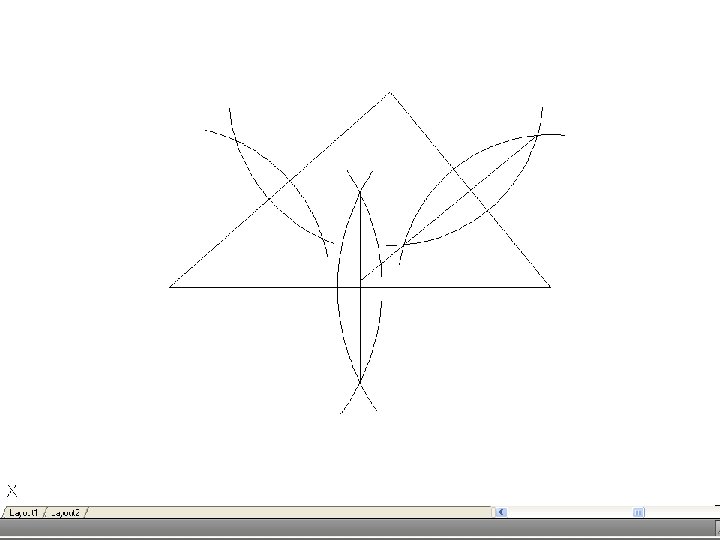
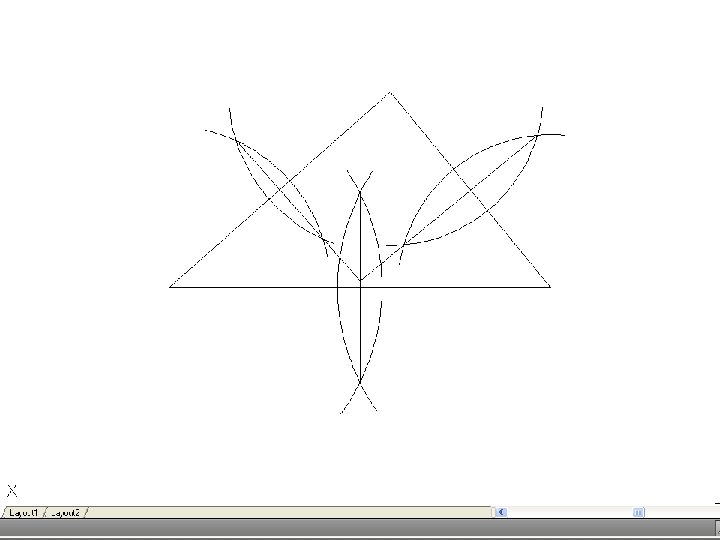
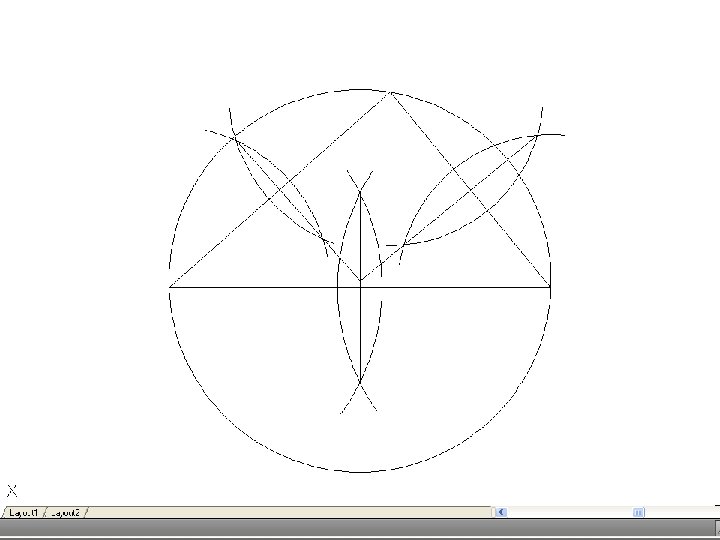
• To bisect an angle – Draw the given angle ABC and from the apex B draw and arc of radius R to cut AB and CD at D and E. R may be any convenient radius. With D and E as centers and radius R’, draw two arcs to meet F. Again, R’ may be any convenient radius. Join FB to bisect the angle.

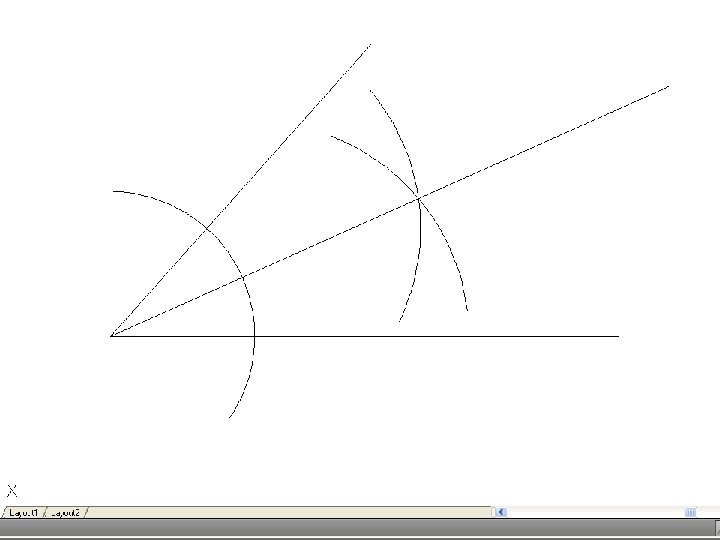
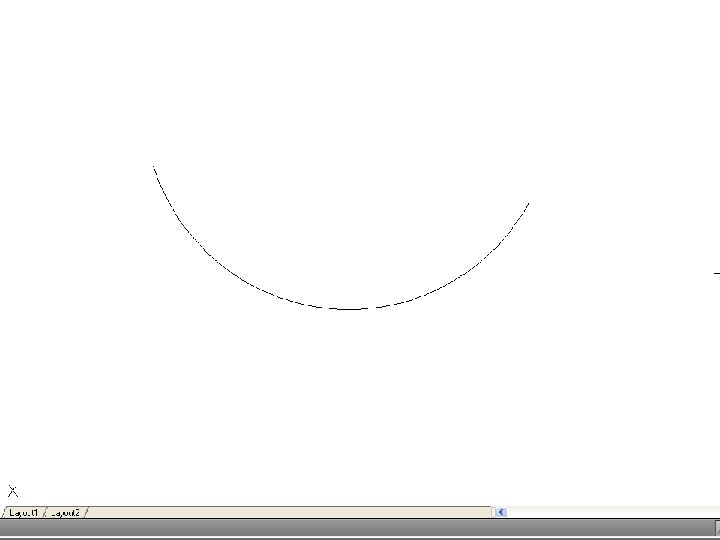
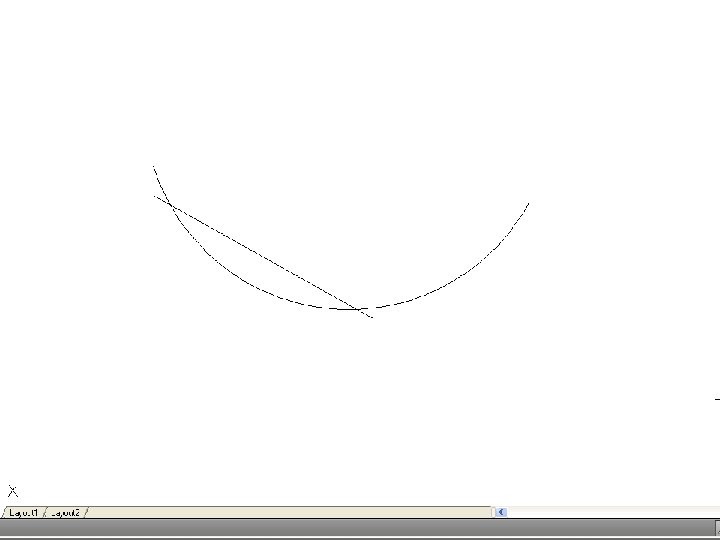
• To find the center of an arc – Select three points, A, B and C on the arc and join AB and BC. Bisect these lines and produce the bisectors to meet at O. O is the center of the arc.

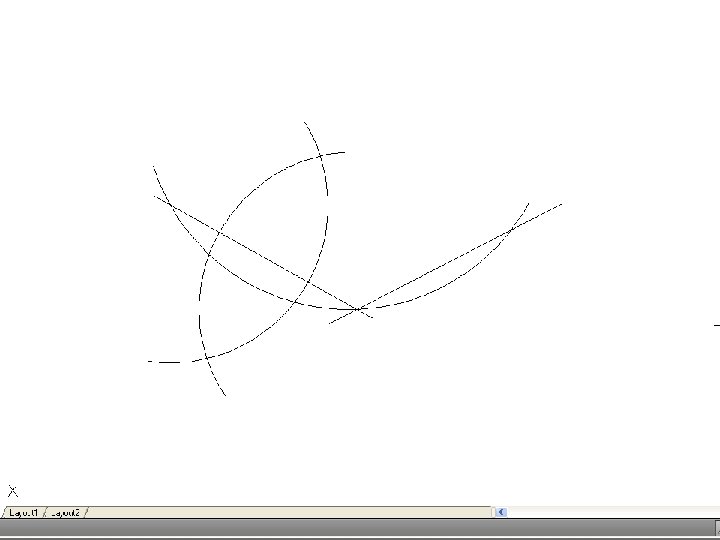
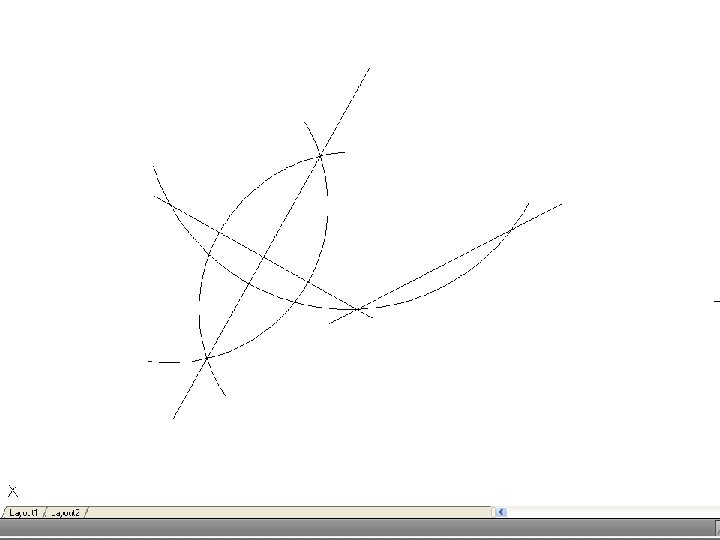
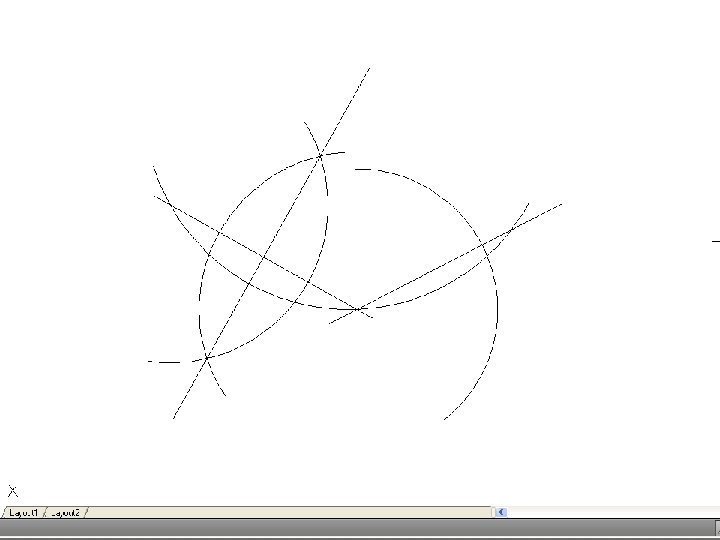
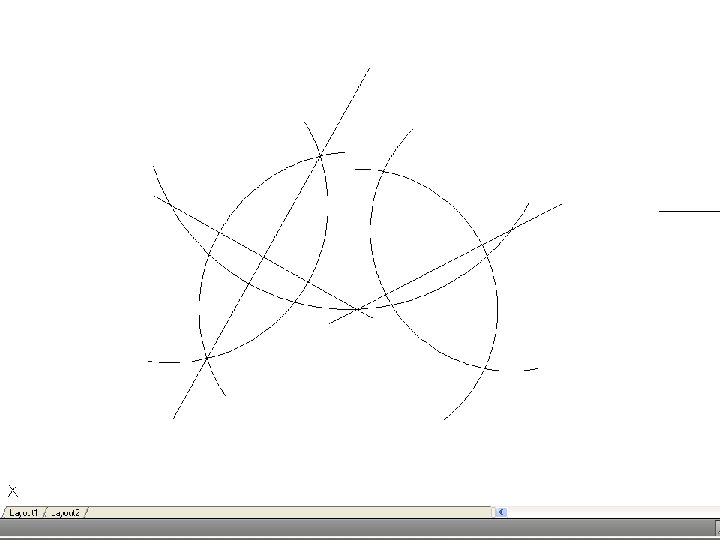
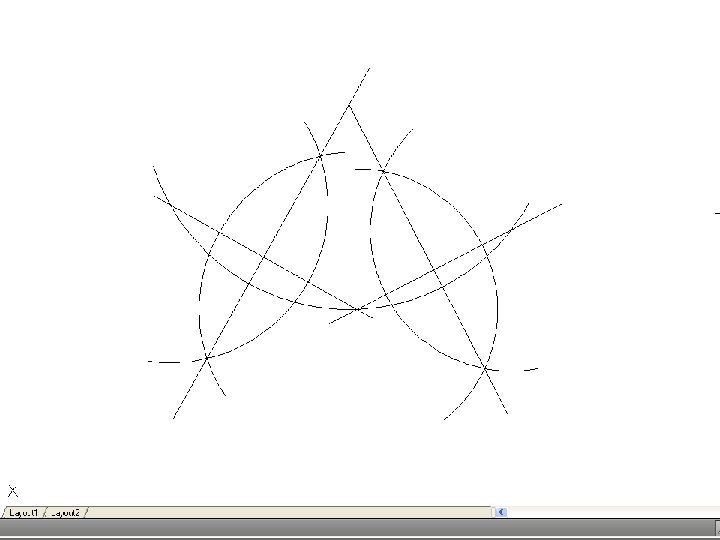
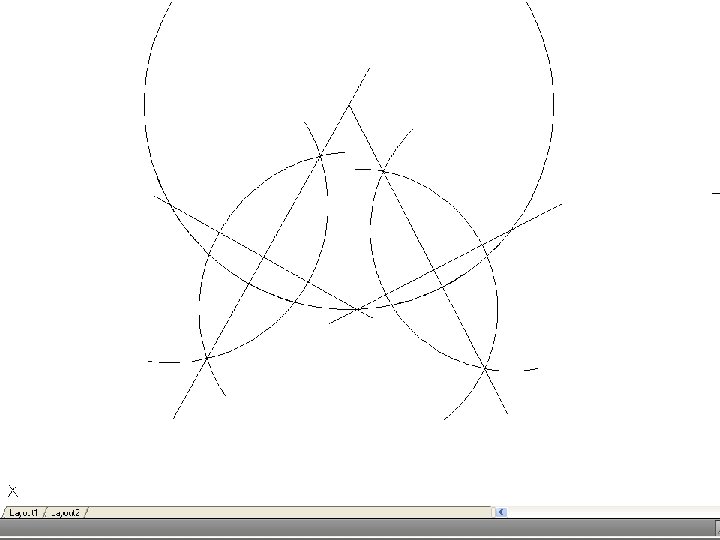
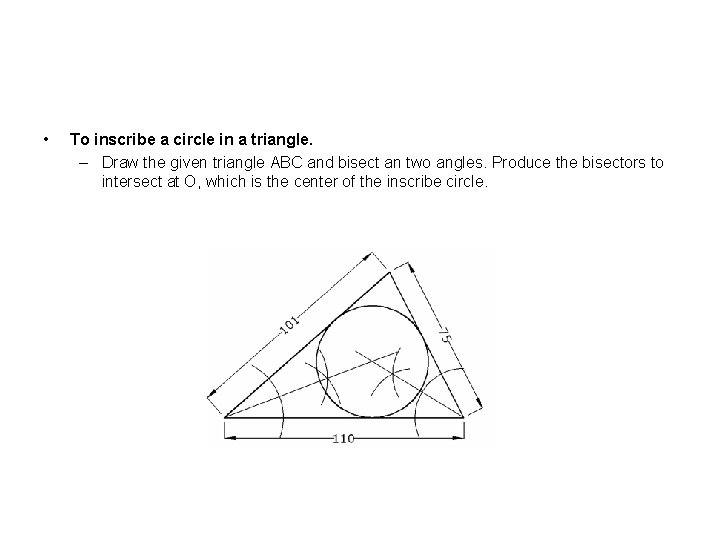
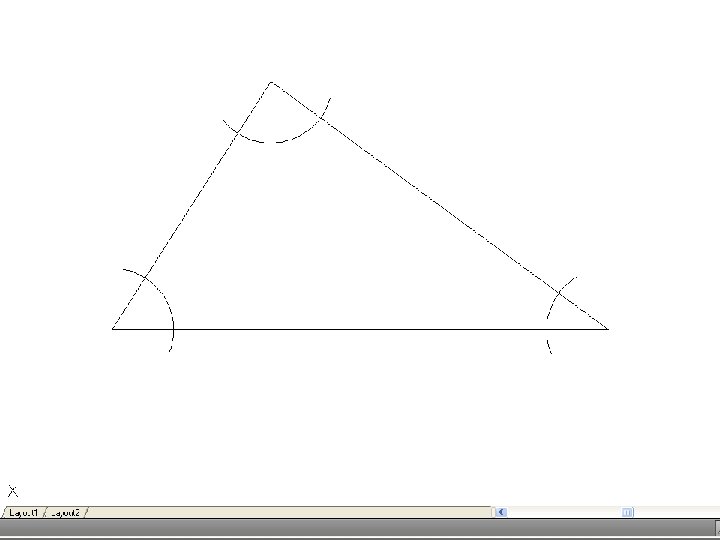
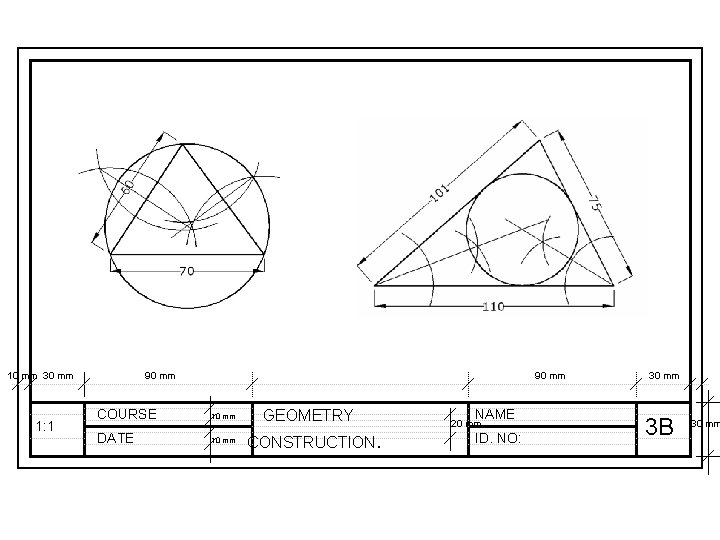
• To inscribe a circle in a triangle. – Draw the given triangle ABC and bisect an two angles. Produce the bisectors to intersect at O, which is the center of the inscribe circle.

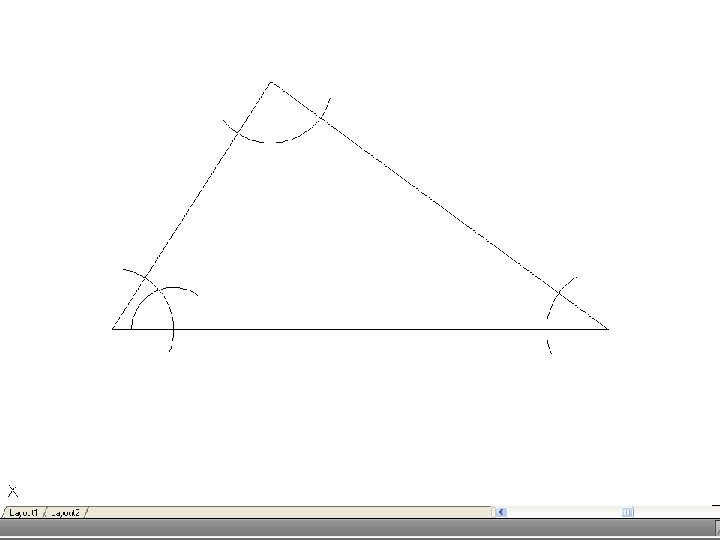
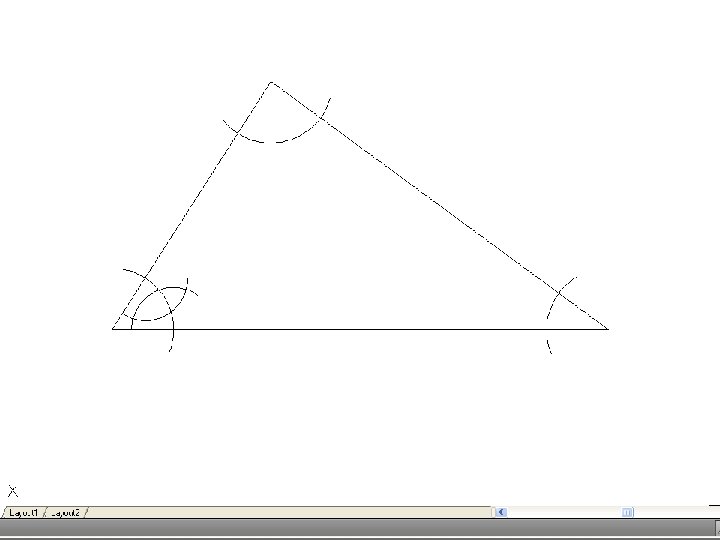
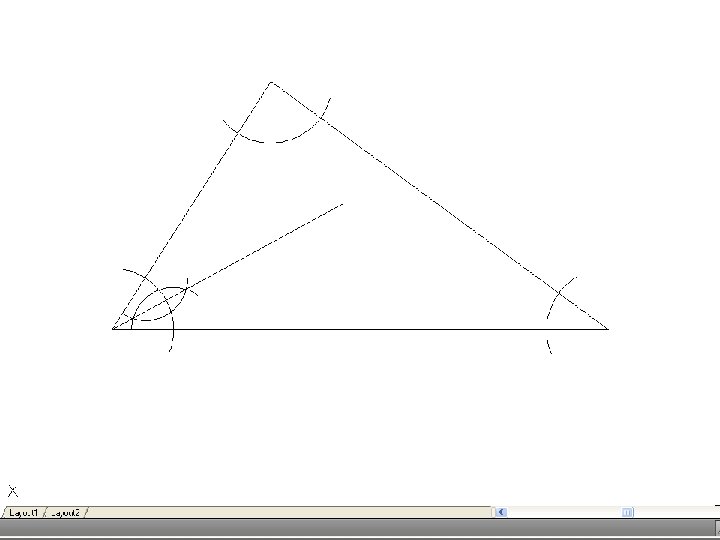
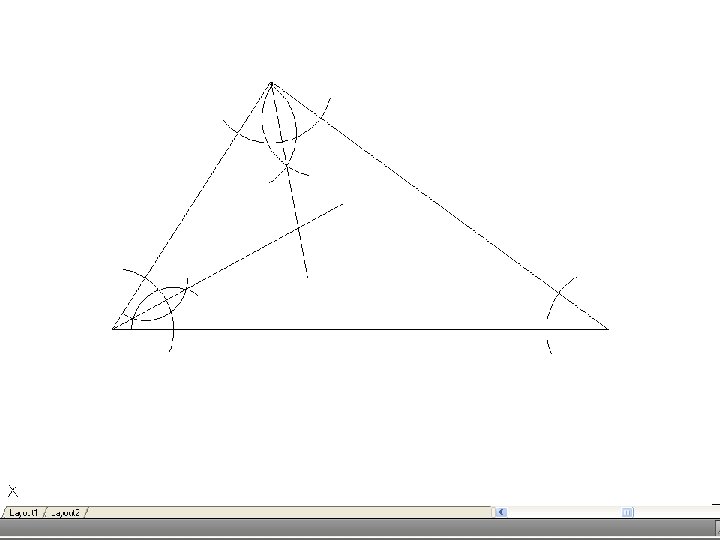
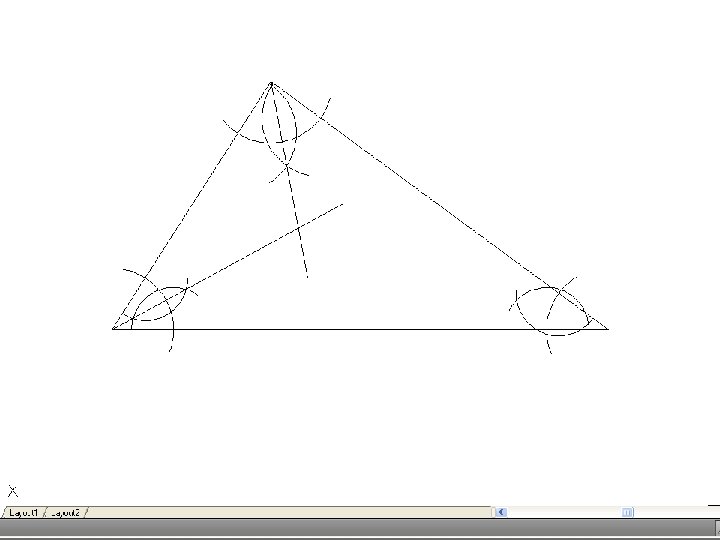
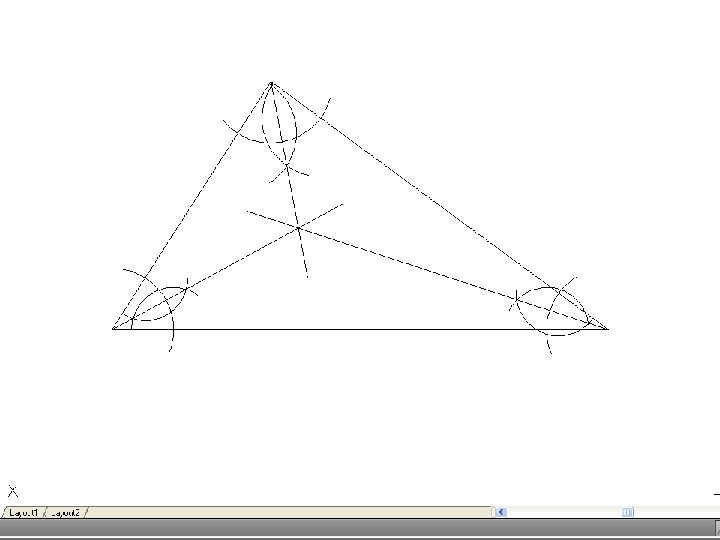
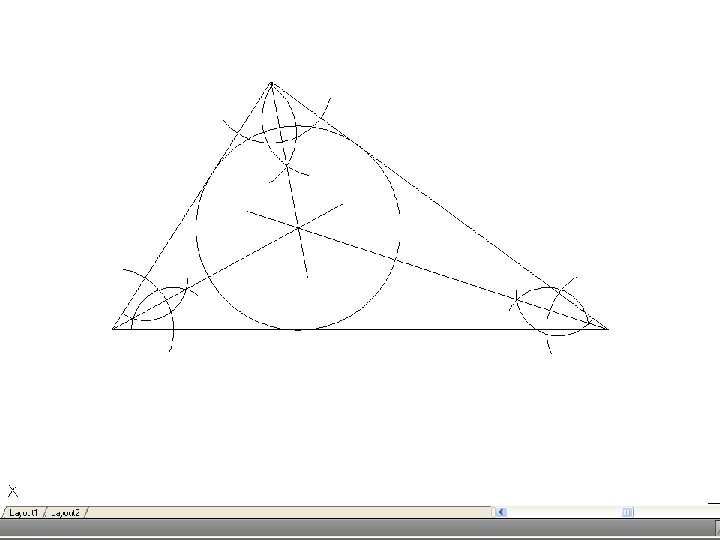
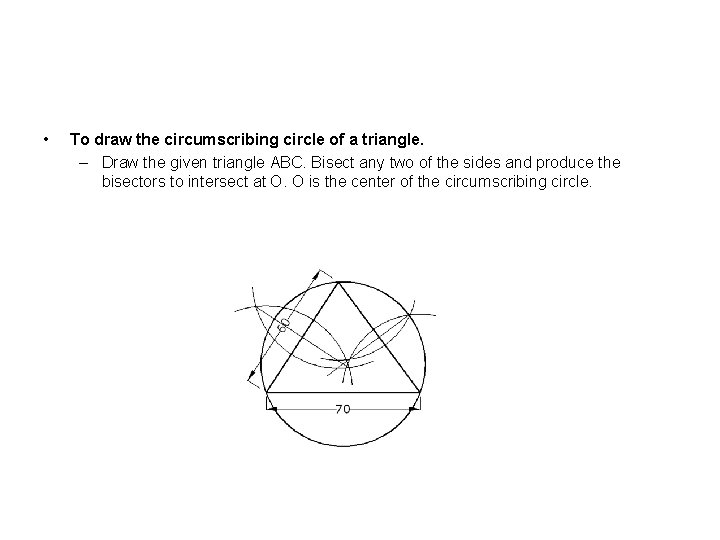
• To draw the circumscribing circle of a triangle. – Draw the given triangle ABC. Bisect any two of the sides and produce the bisectors to intersect at O. O is the center of the circumscribing circle.

10 mm 30 mm 1: 1 90 mm COURSE 10 mm DATE 10 mm GEOMETRY CONSTRUCTION. NAME 20 mm ID. NO: 30 mm 3 A 30 mm

10 mm 30 mm 1: 1 90 mm COURSE 10 mm DATE 10 mm GEOMETRY CONSTRUCTION. NAME 20 mm ID. NO: 30 mm 3 B 30 mm

Geometrical Construction • To bisect a line – Draw the given line AB, with centers A and B and radius R greater than half of AB, draw arcs to intersect a t C and D. Join CD, when E will be the mid point of the line. Also CD will be perpendicular to AB • To divide a line into a number of equal parts – From one end of the given line (say A), draw AD at any convenient angle. Using dividers or a scale, mark off from A on AC the required number of equal parts, making them of any suitable length. Jon the last point to B on the given line, and through the other points draw parallels to this line to cut the given line. This construction makes use of the properties of similar triangles. • To divide a line in a given proportion – Suppose the proportion to be 2 : 3. using the previous construction, proceed as if to divide the line into 5 parts (2 plus 3) but only draw a line through point 2 on AD. Then AB will be divided in the required proportion.

• To bisect an angle – Draw the given angle ABC and from the apex B draw and arc of radius R to cut AB and CD at D and E. R may be any convenient radius. With D and E as centers and radius R’, draw two arcs to meet F. Again, R’ may be any convenient radius. Join FB to bisect the angle. • To find the center of an arc – Select three points, A, B and C on the arc and join AB and BC. Bisect these lines and produce the bisectors to meet at O. O is the center of the arc. • To inscribe a circle in a triangle. – Draw the given triangle ABC and bisect an two angles. Produce the bisectors to intersect at O, which is the center of the inscribe circle. • To draw the circumscribing circle of a triangle. – Draw the given triangle ABC. Bisect any two of the sides and produce the bisectors to intersect at O. O is the center of the circumscribing circle.