Geometric Sequences Dr Shildneck Geometric Sequences An geometric

Geometric Sequences Dr. Shildneck

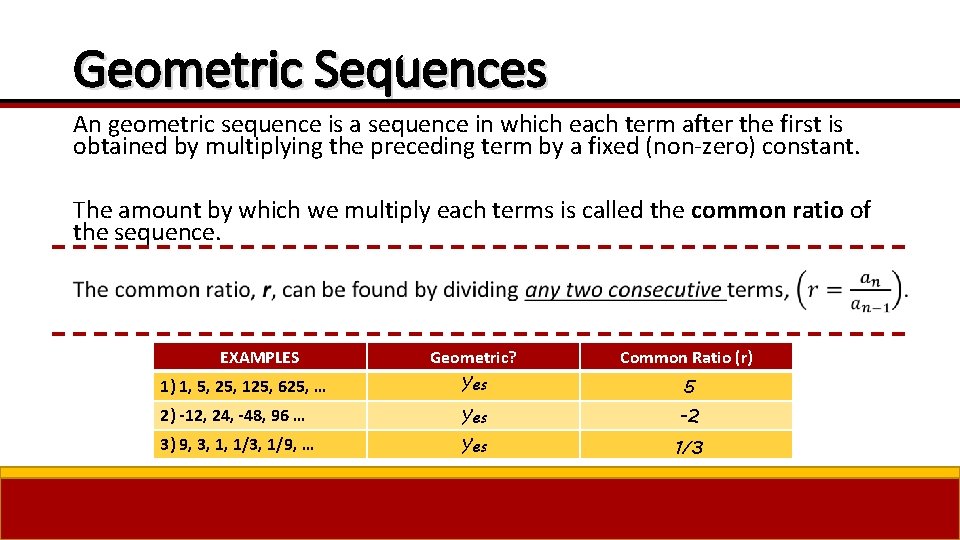
Geometric Sequences An geometric sequence is a sequence in which each term after the first is obtained by multiplying the preceding term by a fixed (non-zero) constant. The amount by which we multiply each terms is called the common ratio of the sequence. EXAMPLES Geometric? Common Ratio (r) 1) 1, 5, 25, 125, 625, … Yes 5 2) -12, 24, -48, 96 … Yes -2 3) 9, 3, 1, 1/3, 1/9, … Yes 1/3

Geometric Functions A geometric function with domain = {all positive integers} and range = {an} has a graph that consists of (only) points that lie on an exponential curve. Thus, an geometric sequence can be thought of as an exponential function whose domain is the set of all positive integers.

Finding the Equation of an Geometric Function 1. Find the common ratio, r. 2. Make a table and compare each term value to its input (position) in the sequence. 3. Find the first term (an). 4. Use the first term and powers of r (using n in the exponent) to write a relationship between the position and the sequence. [Example 1] Write the equation for the sequence 1, 2, 4, 8, 16, 32, 64, 128, …

th Developing a Formula for the n Term Find the equation for each term in an geometric sequence, based on the given first term (a 1) and common ratio (r). a 1 = a 1 a 2 = a 1 (r) a 3 = a 1 (r)(r) = a 1 (r)2 a 4 = a 1 (r)(r)(r) = a (r)3 1 a 5 = a (r)(r) = a (r)4 1 1

th Developing a Formula for the n Term Now looking at the pattern below, how might we write an equation for the nth term (an) based on the first term (a 1) and the common ratio (r). a 1 = a 1 a 2 = a 1 (r)1 a 3 = a 1 (r)2 a 4 = a 1 (r)3 a 5 = a 1 (r)4 What do you notice about n and the number of r’s you need to multiply for the term?

th A Formula for the n Arithmetic Sequence Term of an Given a first term (a 1) and the common difference (d), The nth term (an) of an arithmetic sequence can be found using the formula n-1 an = a 1(r)

Examples [Example 2] Find the 8 th term of the geometric sequence whose first term is -4 and common ratio is -2.

Examples [Example 3] Find the general nth term for the sequence with first term is ¼ and common ratio is 8.

Examples [Example 4] Find the general nth term of the sequence.

Examples [Example 5] Find the nth term of a geometric sequence whose third term is 28 and seventh term in 448.

Examples [Example 6] Find the formula for the nth term of an geometric sequence whose 4 th term is -24 and 7 th term is 192.

ASSIGNMENT YOUR TEXT Page 615 #1 -27 odd