Geometric Sequences ALGEBRA 1 LESSON 6 4 For

Geometric Sequences ALGEBRA 1 LESSON 6 -4 (For help, go to Lesson 5 -6. ) Find the common difference of each sequence. 1. 1, 3, 5, 7, . . . 2. 19, 17, 15, 13, . . . 3. 1. 3, 0. 1, – 1. 1, – 2. 3, . . . 4. 18, 21. 5, 28. 5, . . . Use inductive reasoning to find the next two numbers in each pattern. 5. 2, 4, 8, 16, . . . 6. 4, 12, 36, . . . 7. 0. 2, 0. 4, 0. 8, 1. 6, . . . 8. 200, 100, 50, 25, . . . 6 -4
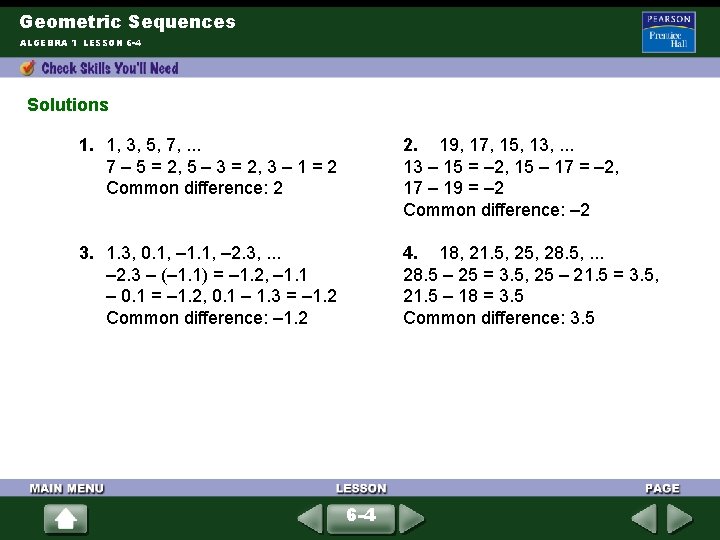
Geometric Sequences ALGEBRA 1 LESSON 6 -4 Solutions 1. 1, 3, 5, 7, . . . 7 – 5 = 2, 5 – 3 = 2, 3 – 1 = 2 Common difference: 2 2. 19, 17, 15, 13, . . . 13 – 15 = – 2, 15 – 17 = – 2, 17 – 19 = – 2 Common difference: – 2 3. 1. 3, 0. 1, – 1. 1, – 2. 3, . . . – 2. 3 – (– 1. 1) = – 1. 2, – 1. 1 – 0. 1 = – 1. 2, 0. 1 – 1. 3 = – 1. 2 Common difference: – 1. 2 4. 18, 21. 5, 28. 5, . . . 28. 5 – 25 = 3. 5, 25 – 21. 5 = 3. 5, 21. 5 – 18 = 3. 5 Common difference: 3. 5 6 -4

Geometric Sequences ALGEBRA 1 LESSON 6 -4 Solutions (continued) 5. 2, 4, 8, 16, . . . 2(2) = 4, 4(2) = 8, 8(2) = 16, 16(2) = 32, 32(2) = 64 Next two numbers: 32, 64 6. 4, 12, 36, . . . 4(3) = 12, 12(3) = 36, 36(3) = 108, 108(3) = 324 Next two numbers: 108, 324 7. 0. 2, 0. 4, 0. 8, 1. 6, . . . (0. 2)2 = 0. 4, 0. 4(2) = 0. 8, 0. 8(2) = 1. 6, 1. 6(2) = 3. 2, 3. 2(2) = 6. 4 Next two numbers: 3. 2, 6. 4 8. 200, 100, 50, 25, . . . 200 2 = 100, 100 2 = 50, 50 2 = 25, 25 2 = 12. 5, 12. 5 2 = 6. 25 6 -4

Geometric Sequences ALGEBRA 1 LESSON 6 -4 Find the common ratio of each sequence. a. 3, – 15, 75, – 375, . . . 3 – 15 (– 5) 75 (– 5) – 375 (– 5) The common ratio is – 5. 3 3 3 b. 3, 2 , 4 , 8 , . . . 3 2 3 1 2 3 4 1 2 1 The common ratio is . 2 3 8 1 2 6 -4

Geometric Sequences ALGEBRA 1 LESSON 6 -4 Find the next three terms of the sequence 5, – 10, 20, – 40, . . . 5 – 10 (– 2) 20 (– 2) – 40 (– 2) The common ratio is – 2. The next three terms are – 40(– 2) = 80, 80(– 2) = – 160, and – 160(– 2) = 320. 6 -4

Geometric Sequences ALGEBRA 1 LESSON 6 -4 Determine whether each sequence is arithmetic or geometric. a. 162, 54, 18, 6, . . . 62 54 1 3 18 1 3 6 1 3 The sequence has a common ratio. The sequence is geometric. 6 -4
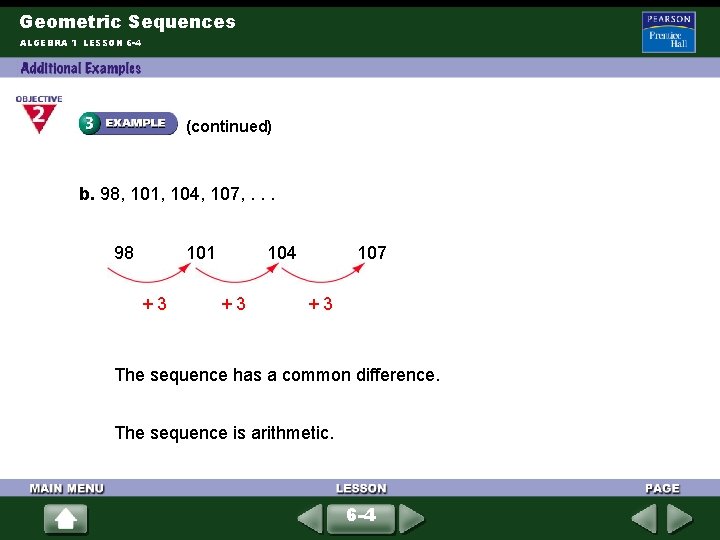
Geometric Sequences ALGEBRA 1 LESSON 6 -4 (continued) b. 98, 101, 104, 107, . . . 98 101 + 3 104 + 3 107 + 3 The sequence has a common difference. The sequence is arithmetic. 6 -4

Geometric Sequences ALGEBRA 1 LESSON 6 -4 Find the first, fifth, and tenth terms of the sequence that has the rule A(n) = – 3(2)n – 1. first term: A(1) = – 3(2)1 – 1 = – 3(2)0 = – 3(1) = – 3 fifth term: A(5) = – 3(2)5 – 1 = – 3(2)4 = – 3(16) = – 48 tenth term: A(10) = – 3(2)10 – 1 = – 3(2)9 = – 3(512) = – 1536 6 -4

Geometric Sequences ALGEBRA 1 LESSON 6 -4 Suppose you drop a tennis ball from a height of 2 meters. On each bounce, the ball reaches a height that is 75% of its previous height. Write a rule for the height the ball reaches on each bounce. In centimeters, what height will the ball reach on its third bounce? The first term is 2 meters, which is 200 cm. Draw a diagram to help understand the problem. 6 -4
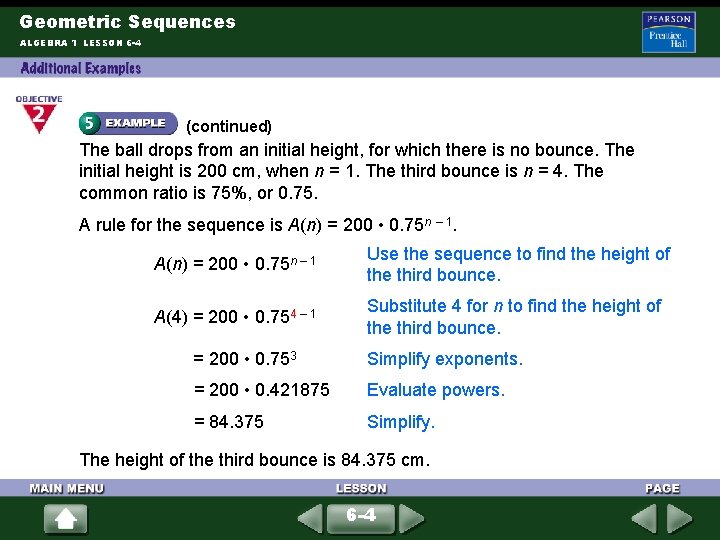
Geometric Sequences ALGEBRA 1 LESSON 6 -4 (continued) The ball drops from an initial height, for which there is no bounce. The initial height is 200 cm, when n = 1. The third bounce is n = 4. The common ratio is 75%, or 0. 75. A rule for the sequence is A(n) = 200 • 0. 75 n – 1 Use the sequence to find the height of the third bounce. A(4) = 200 • 0. 754 – 1 Substitute 4 for n to find the height of the third bounce. = 200 • 0. 753 Simplify exponents. = 200 • 0. 421875 Evaluate powers. = 84. 375 Simplify. The height of the third bounce is 84. 375 cm. 6 -4

Geometric Sequences ALGEBRA 1 LESSON 6 -4 1. Find the common ratio of the geometric sequence – 3, 6, – 12, 24, . . . – 2 2. Find the next three terms of the sequence 243, 81, 27, 9, . . . 1 3, 1, 3 3. Determine whether each sequence is arithmetic or geometric. a. 37, 34, 31, 28, . . . arithmetic b. 8, – 4, 2, – 1, . . . geometric 4. Find the first, fifth, and ninth terms of the sequence that has the rule A(n) = 4(5)n– 1. 4, 2500, 1, 562, 500 5. Suppose you enlarge a photograph that is 4 in. wide and 6 in. long so that its dimensions are 20% larger than its original size. Write a rule for the length of the copies. What will be the length if you enlarge the photograph five times? (Hint: The common ratio is not just 0. 2. You must add 20% to 100%. ) A(n) = 6(1. 2)n-1; about 14. 9 in. 6 -4
- Slides: 11