Geometric objects and Transformations Workshop on Computer Graphics

Geometric objects and Transformations Workshop on Computer Graphics & Visualization 1 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

Objectives Introduce standard transformations Rotation Translation Scaling Shear Derive homogeneous coordinate transformation matrices Learn to build arbitrary transformation matrices from simple transformations 2 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

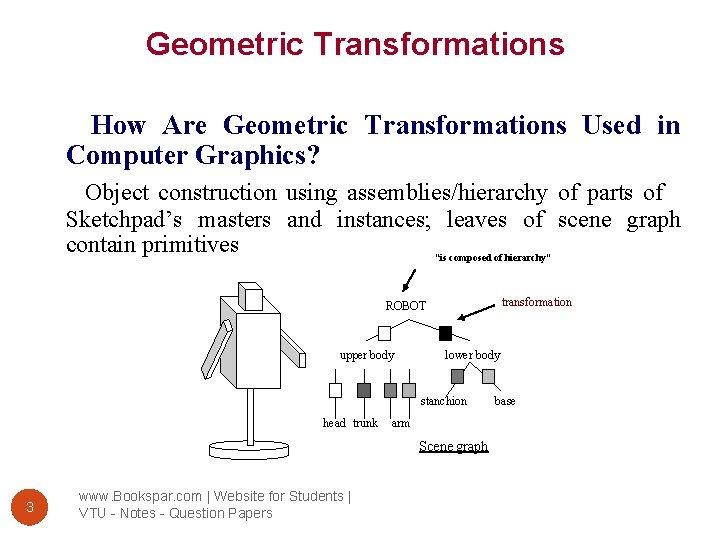
Geometric Transformations How Are Geometric Transformations Used in Computer Graphics? Object construction using assemblies/hierarchy of parts of Sketchpad’s masters and instances; leaves of scene graph contain primitives “is composed of hierarchy” transformation ROBOT upper body lower body stanchion head trunk arm Scene graph 3 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers base

Aid to realism objects, Help form 3 D “object hypothesis” kinesthetic feedback as user manipulates objects or synthetic camera City planning application program Applications use geometric transformations to change position, orientation, and size of the objects CAD 4 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

2 D Object Definition • Lines and Polylines: lines drawn between ordered points • Same first and last point make closed polyline or • 5 polygon If it does not intersect itself, called simple polygon www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

Convex vs. Concave Polygons Convex: For every pair of points in the polygon, the line between them is fully contained in the polygon Concave: Not convex: some two points in the polygon are joined by a line not fully contained in the polygon 6 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

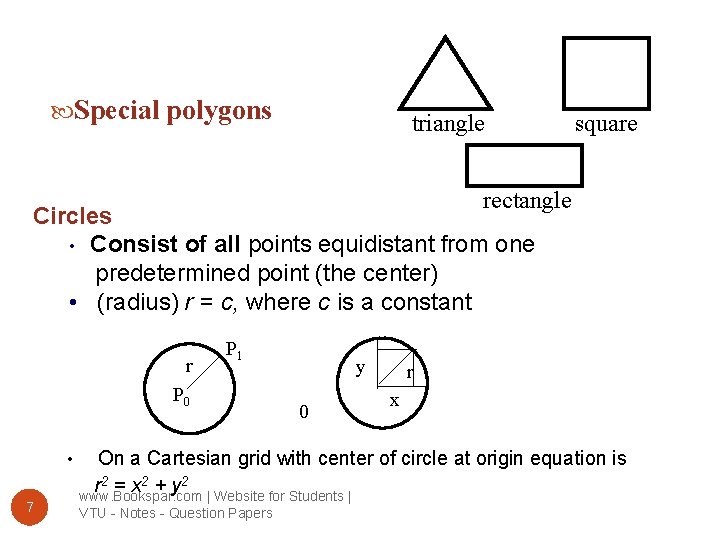
Special polygons triangle square rectangle Circles • Consist of all points equidistant from one predetermined point (the center) • (radius) r = c, where c is a constant r P 1 P 0 • 7 y 0 r x On a Cartesian grid with center of circle at origin equation is 2 = x 2 + y 2 r www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

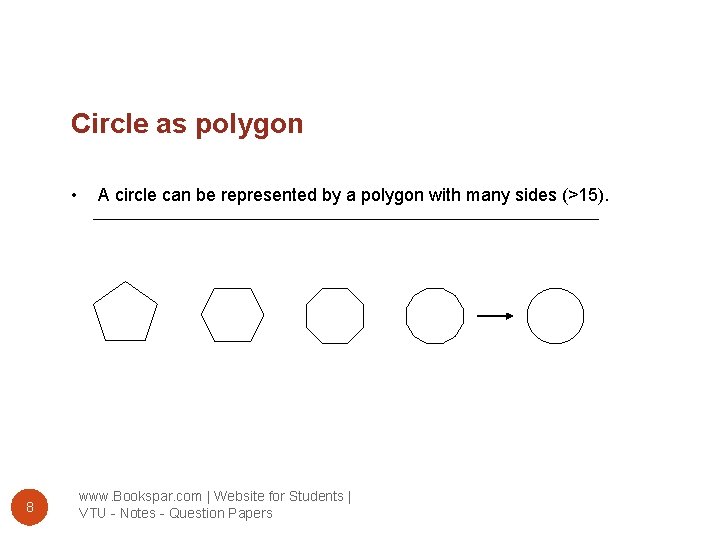
Circle as polygon • 8 A circle can be represented by a polygon with many sides (>15). www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

Ellipses A circle scaled along the x or y axis 6 6 5 5 4 4 3 3 2 2 1 1 0 0 1 2 3 4 5 6 7 8 9 10 Example: height, on y-axis, remains 3, while length, on xaxis, changes from 3 to 6 9 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

2 D to 3 D Object Definition Vertices in motion (“Generative object description”) • Line is drawn by tracing path of a point as it moves (one dimensional entity) • Square drawn by tracing vertices of a line as it moves perpendicularly to itself (two dimensional entity) • Cube drawn by tracing paths of vertices of a square as it moves perpendicularly to itself (3 -D entity) • Circle drawn by swinging a point at a fixed length around a center point 10 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

Building 3 D Primitives • 11 Triangles and tri-meshes www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

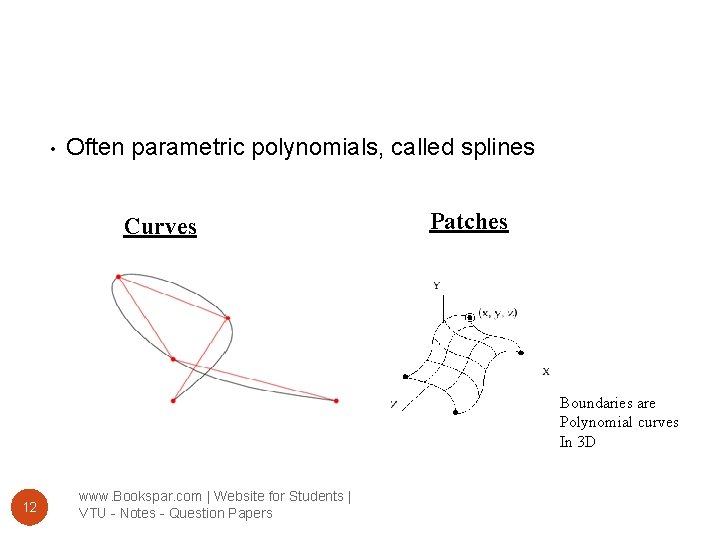
• Often parametric polynomials, called splines Curves Patches Boundaries are Polynomial curves In 3 D 12 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

Transformations in Open. GL Modeling Viewing orient camera projection Animation Map to screen 13 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

Camera Analogy & Transformations 3 D is just like taking a photograph Projection transformations adjust the lens of the camera Viewing transformations tripod–define position and orientation of the viewing volume in the world Modeling transformations moving the model Viewport transformations enlarge or reduce the physical photograph 14 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

Coordinate Systems & Transformations Steps in Forming an Image § specify geometry (world coordinates) § specify camera (camera coordinates) § project (window coordinates) § map to viewport (screen coordinates) Each step uses transformations Every transformation is equivalent to a change in coordinate systems (frames) 15 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

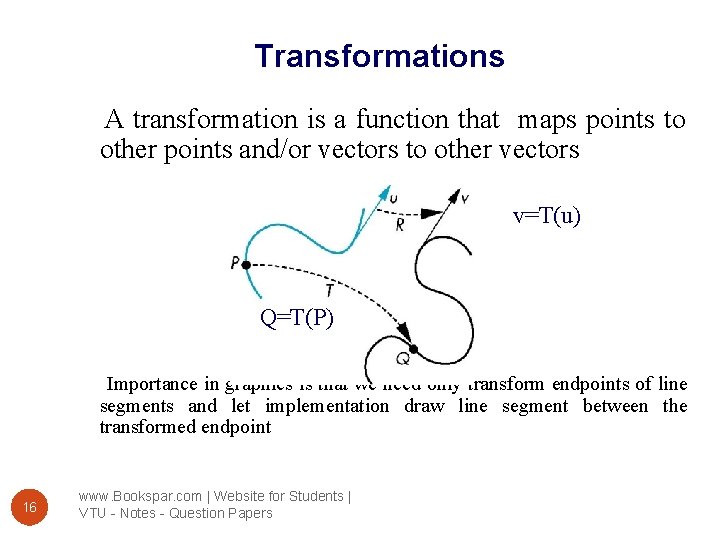
Transformations A transformation is a function that maps points to other points and/or vectors to other vectors v=T(u) Q=T(P) Importance in graphics is that we need only transform endpoints of line segments and let implementation draw line segment between the transformed endpoint 16 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers

Affine Transformations which preserve geometry § lines, polygons, quadrics Affine = line preserving Rotation, translation, scaling § Projection § Concatenation (composition) § Characteristic transformations of many physically Rigid body transformations: rotation, translation Scaling, shear 17 www. Bookspar. com | Website for Students | VTU - Notes - Question Papers important