Geometric Objects and Transformations Chapter 4 Points Scalars

Geometric Objects and Transformations Chapter 4

Points, Scalars and Vectors § Points - position in space § Scalars - real numbers, complex numbers obey a set of rules that are abstractions of arithmetic store values such as distance § Vectors - directed line segment

Vector Arithmetic § B = 2 A §C=A+B § Head to tail rule § E = -A § Inverse § Zero vector = E + A

Point Arithmetic § Can’t add p 1 + p 2 = p 3 § Can’t multiply p 1 * 2 = p 2 § What can you do to produce a 2 nd point from a 1 st? § p 1 + V = p 2 § V = p 2 - p 1

Important Vector Concepts § Normal Vector § A vector at a right angle to a surface. § Graphics Usage of Normal Vector § Used to figure out similarity of direction which is necessary for lighting § More precisely, how much light should fall on a surface is calculated by the similarity of the surface normal and the vector between the light source and the surface. § Similarity of direction = vector dot product

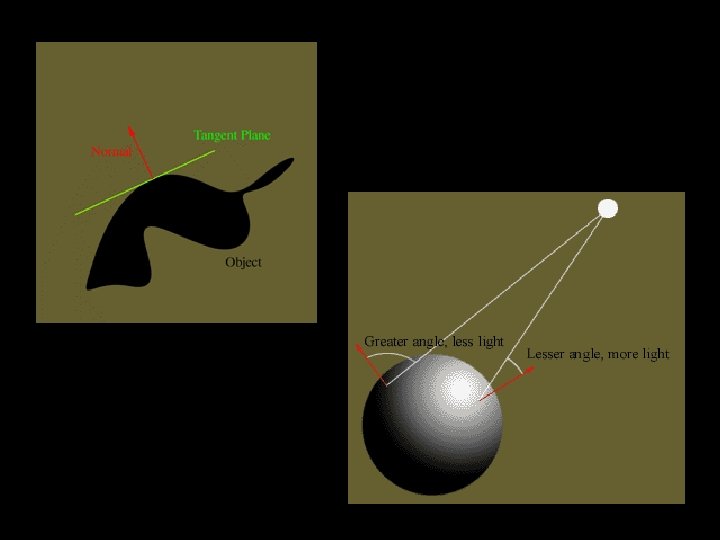
Vector Dot Product § For vectors of length 1 (unit vectors), the dot product is the length of the projection of one vector onto the other. § If the dot product = § 1: the vectors point in the same direction § 0: the vectors are at right angles § -1: the vectors point in opposite directions

Vector Cross Product § The cross product of two vectors A and B is another vector at right angles to the plane created by A and B

Defining a Coordinate Space § Need to know 1. The origin (or displacement vector) 2. The basis vectors - The direction and distance for +1 movement along each axis § § This definition is relative To plot a point 1. Begin at origin 2. Travel along the x basis vector [direction] scaled by x coord, then along the y basis vector scaled by the y coord, then finally along the z basis vector scaled by the z coord.

Transformations § Prior to rendering: view, locate and orient § eye / camera position § 3 D geometry § Manage the matrices § including the matrix stack § Combine (composite) transformations

Camera Analogy

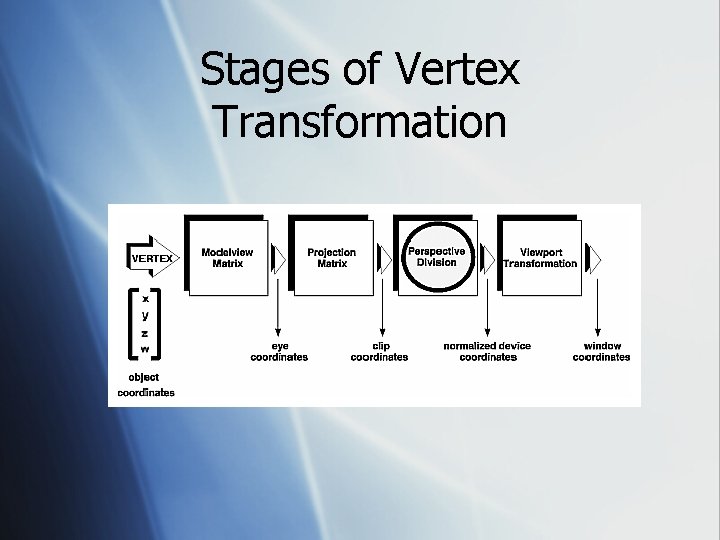
Stages of Vertex Transformation

Transformations § 45 -degree counterclockwise rotation about the origin around the z-axis § a translation down the x-axis

Order of Transformations gl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity(); gl. Mult. Matrixf(N); /* apply transformation N */ gl. Mult. Matrixf(M); /* apply transformation M */ gl. Mult. Matrixf(L); /* apply transformation L */ gl. Begin(GL_POINTS); gl. Vertex 3 f(v); /* draw transformed vertex v */ gl. End(); § transformed vertex is NMLv

Translation § void gl. Translate{fd} (TYPE x, TYPE y, TYPE z); § Multiplies the current matrix by a matrix that moves (translates) an object by the given x, y, and z values

Rotation § void gl. Rotate{fd}(TYPE angle, TYPE x, TYPE y, TYPE z); § Multiplies the current matrix by a matrix that rotates an object in a counterclockwise direction about the ray from the origin through the point (x, y, z). The angle parameter specifies the angle of rotation in degrees.

Scale § void gl. Scale{fd} (TYPEx, TYPE y, TYPEz); § Multiplies the current matrix by a matrix that stretches, shrinks, or reflects an object along the axes.

Vectors 1 2 3 + 2 3 4 3 = 5 7

1 3 1 Matrices § Rectangular array of numbers § A vector in 3 space is a n x 1 matrix or column vector. § Multiplication 1 0 0 0 0 0 1/k 0 0 0 1 x Cos α 0 -sin α 0 0 1 0 0 sin α 0 cos α 0 0 m n 1

Matrix Multiplication § A is an n x m matrix with entries aij § B is an m x p matrix with entries bij § AB is an n x p matrix with entries cij m § cij = ais bsj s=1

2 D Transformations § Translation: Pf = T + P xf = xo + dx yf = yo + dy § Rotation: Pf = R · P xf = xo * cos - yo *sin yf = xo * sin + yo *cos § Scale: Pf = S · P xf = sx * xo yf = sy * yo

Homogeneous Coordinates § Want to treat all transforms in a consistent way so they can be combined easily § Developed in geometry (‘ 46 in cambridge) and applied to graphics § Add a third coordinate to a point (x, y, w) § (x 1, y 1, w 1) is the same point as (x 2, y 2, w 2) if one is a multiple of another § Homogenize a point by dividing by w

Homogeneous Coordinates 1 0 0 1*x 0*x 0 1 0 dx dy 1 + + + · 0*y 1*y 0*y x y 1 + + + dx * 1 dy * 1 1*1

Homogeneous Coordinates 1 0 0 0 1 0 dx dy 1 · x y 1

Homogeneous Coordinates sx 0 0 0 sy 0 0 0 1 · x y 1

Homogeneous Coordinates Cos sin 0 -sin cos 0 0 0 1 · x y 1

Homogeneous Coordinates 1 0 0 0 1 x · y 1 = x y 1 § Identity Maxtrix x point p = point p

Combining 2 D Transformations § Rotate a house about the origin § Rotate the house about one of its corners § translate so that a corner of the house is at the origin § rotate the house about the origin § translate so that the corner returns to its original position

Open. GL Buffers § Color § can be divided into front and back for double buffering § § Alpha Depth Stencil Accumulation

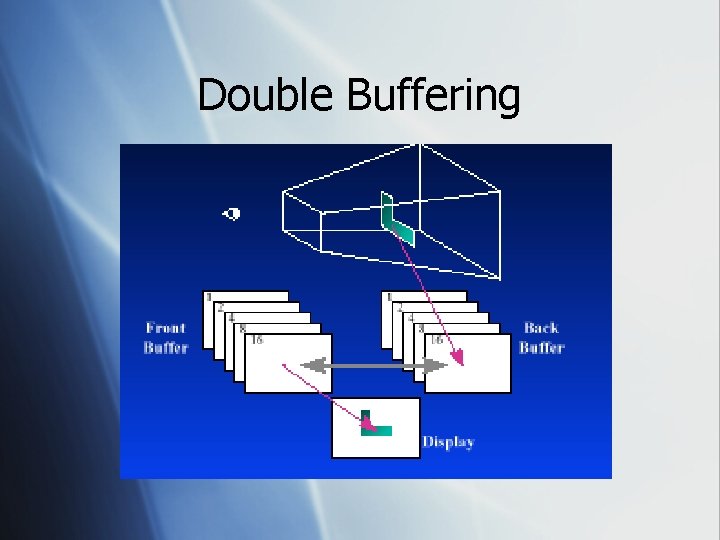
Double Buffering

Animating Using Double Buffering § Request a double buffered color buffer glut. Init. Display. Mode (GLUT_RGB | GLUT_DOUBLE); § Clear color buffer § gl. Clear(GL_COLOR_BUFFER_BIT); § Render Scene § Request swap of front and back buffers § glut. Swap. Buffers(); § Repeat steps 2 -4 for animation.

Depth Buffering

3 D Coords --> Raster coords § Transformations § Clipping § Viewport transformation.

GLUT Solids § § § § § Sphere Cube Cone Torus Dodecahedron Octahedron Tetrahedron Icosahedron Teapot

glut. Solid. Sphere and glut. Wire. Sphere § void glut. Solid. Sphere(GLdouble radius, GLint slices, GLint stacks); § radius - The radius of the sphere. § slices - The number of subdivisions around the Z axis (similar to lines of longitude). § stacks - The number of subdivisions along the Z axis (similar to lines of latitude).

glut. Solid. Cube and glut. Wire. Cube § void glut. Solid. Cube(GLdouble size); § size – length of sides

glut. Solid. Cone and glut. Wire. Cone § void glut. Solid. Cone(GLdouble base, GLdouble height, GLint slices, GLint stacks); § base - The radius of the base of the cone. § height - The height of the cone. § slices - The number of subdivisions around the Z axis. § stacks - The number of subdivisions along the Z axis.

glut. Solid. Torus and glut. Wire. Torus § void glut. Solid. Torus(GLdouble inner. Radius, GLdouble outer. Radius, GLint nsides, GLint rings); § inner. Radius - Inner radius of the torus. § outer. Radius - Outer radius of the torus. § nsides - Number of sides for each radial section. § rings - Number of radial divisions for the torus.

glut. Solid. Dodecahedron and glut. Wire. Dodecahedron § void glut. Solid. Dodecahedron(void);

glut. Solid. Octahedron and glut. Wire. Octahedron. § void glut. Solid. Octahedron(void);

glut. Solid. Tetrahedron and glut. Wire. Tetrahedron § void glut. Solid. Tetrahedron(void);

glut. Solid. Icosahedron and glut. Wire. Icosahedron § void glut. Solid. Icosahedron(void);

glut. Solid. Teapot and glut. Wire. Teapot § void glut. Solid. Teapot(GLdouble size); § size - Relative size of the teapot.

Homework § Project part 2 due 2/19 § Turn in a program that, at a minimum, draws your initial scene.