Geometric Objects 2001 7 6 Computer Graphics Lab

Geometric Objects 2001. 7. 6 Computer Graphics Lab. Sun-Jeong Kim

Points v Single Coordinate Position ® Set the bit value(color code) corresponding to a specified screen position within the frame buffer y set. Pixel (x, y) x 2 Korea University Computer Graphics

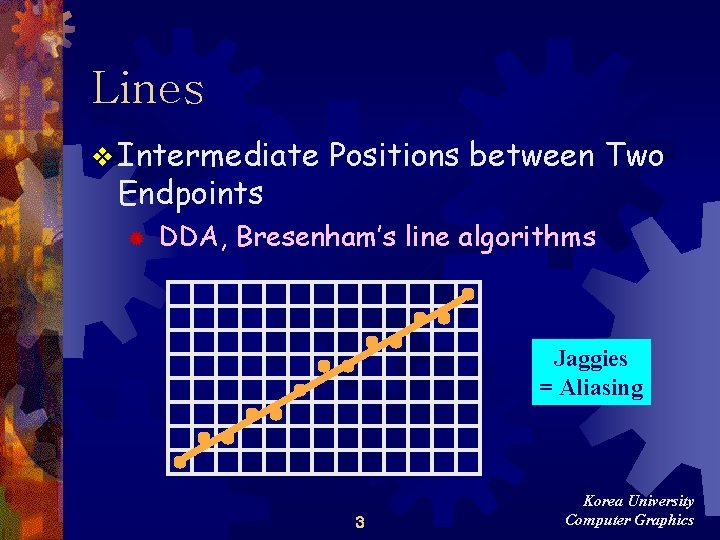
Lines v Intermediate Endpoints ® Positions between Two DDA, Bresenham’s line algorithms Jaggies = Aliasing 3 Korea University Computer Graphics

DDA Algorithm v Digital Differential ® Slope >= 1 Ø ® ® y 2 y 1 Unit y interval = 1 y 1 Slope <= -1 Ø ® Unit x interval = 1 0 < Slope < 1 Ø Analyzer Unit x interval = -1 x 1 x 2 -1 < Slope < 0 Ø Unit y interval = -1 4 Korea University Computer Graphics

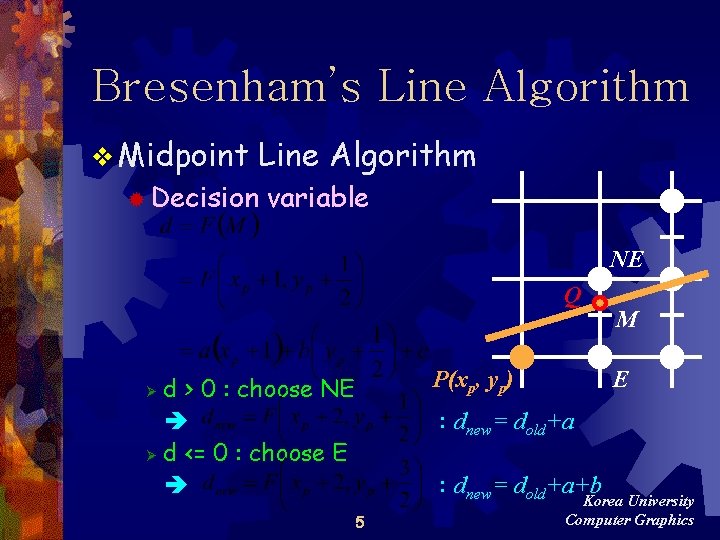
Bresenham’s Line Algorithm v Midpoint ® Decision Line Algorithm variable NE Q P(xp, yp) d > 0 : choose NE Ø d <= 0 : choose E Ø M E : dnew= dold+a+b 5 Korea University Computer Graphics

Bresenham’s Algorithm(cont. ) v Initial Value of d v Update d 6 Korea University Computer Graphics

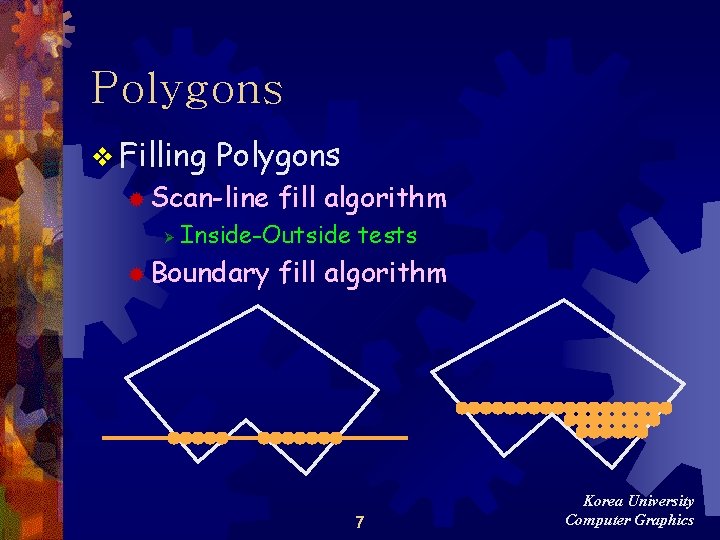
Polygons v Filling Polygons ® Scan-line Ø fill algorithm Inside-Outside tests ® Boundary fill algorithm 7 Korea University Computer Graphics

Scan-Line Polygon Fill v Topological lines Difference between 2 Scan y : intersection edges are opposite sides ® y’ : intersection edges are same side ® y y’ 8 Korea University Computer Graphics

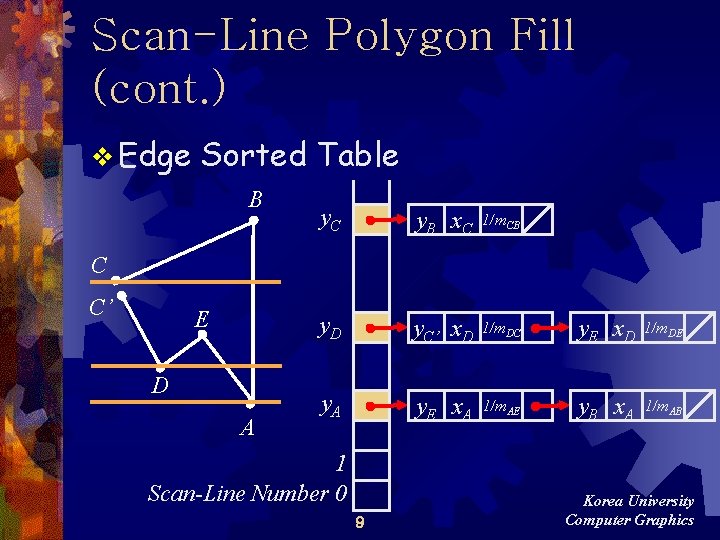
Scan-Line Polygon Fill (cont. ) v Edge Sorted Table B y. C y. B x. C 1/m. CB y. D y. C’ x. D 1/m. DC y. E x. D 1/m. DE y. A y. E x. A 1/m. AE y. B x. A 1/m. AB C C’ E D A 1 Scan-Line Number 0 9 Korea University Computer Graphics

Inside-Outside Tests v Self-Intersections ® Odd-Even rule ® Nonzero winding number rule exterior interior 10 Korea University Computer Graphics

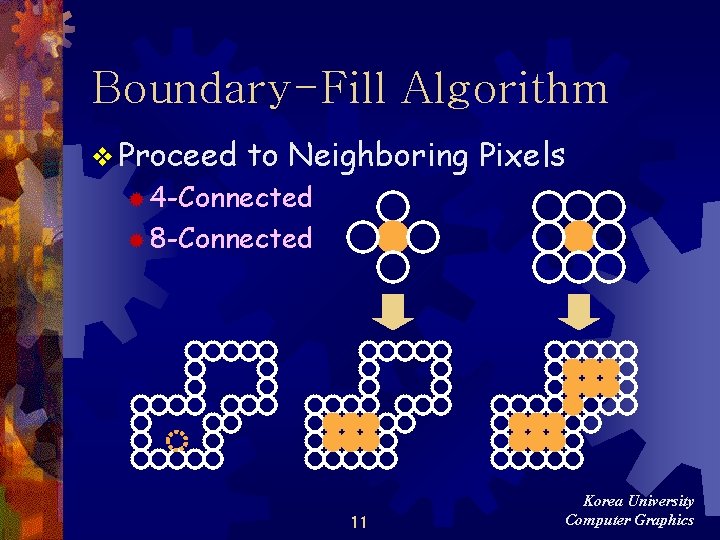
Boundary-Fill Algorithm v Proceed to Neighboring Pixels ® 4 -Connected ® 8 -Connected 11 Korea University Computer Graphics

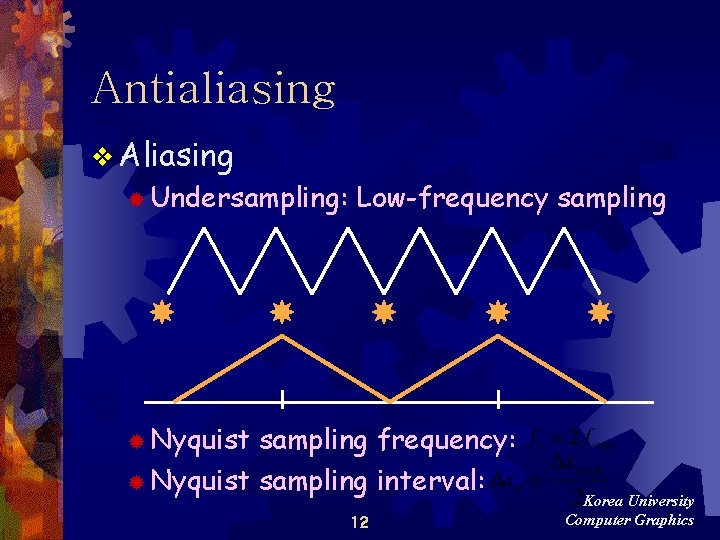
Antialiasing v Aliasing ® Undersampling: Low-frequency sampling ® Nyquist sampling frequency: ® Nyquist sampling interval: 12 Korea University Computer Graphics

Antialiasing (cont. ) v Supersampling (Postfiltering) ® Pixel-weighting masks v Area Sampling (Prefiltering) v Pixel Phasing ® Shift the display location of pixel areas ® Micropositioning the electron beam in relation to object geometry 13 Korea University Computer Graphics

Supersampling v Subpixels ® Increase resolution 22 (10, 20): Maximum Intensity 21 (11, 21): Next Highest Intensity (11, 20): Lowest Intensity 20 10 11 12 14 Korea University Computer Graphics

Pixel-Weighting Masks v Give More Weight to Supixels Near the Center of a Pixel Area 1 2 4 2 15 1 4 1 Korea University Computer Graphics

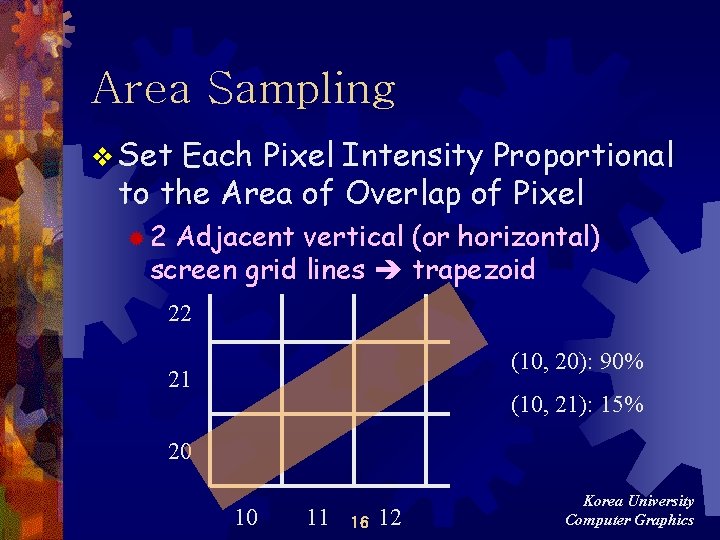
Area Sampling v Set Each Pixel Intensity Proportional to the Area of Overlap of Pixel ® 2 Adjacent vertical (or horizontal) screen grid lines trapezoid 22 (10, 20): 90% 21 (10, 21): 15% 20 10 11 16 12 Korea University Computer Graphics

Filtering Techniques v Filter Functions (Weighting Surface) Box Filter Cone Filter 17 Gaussian Filter Korea University Computer Graphics

Mathematics for CG

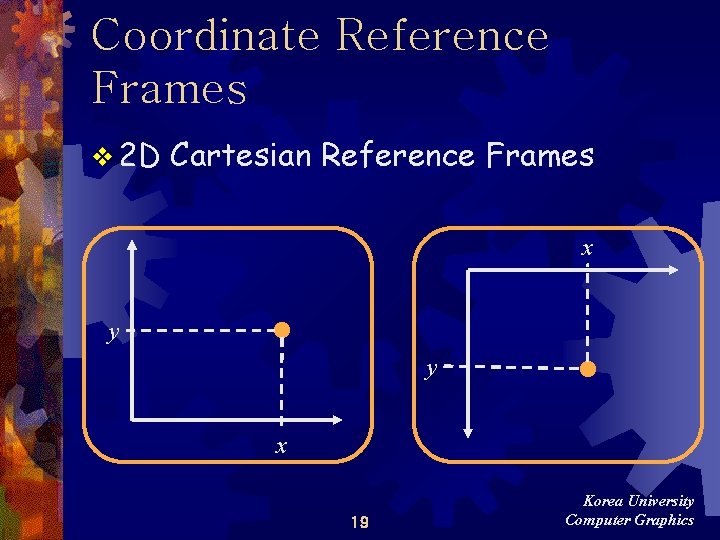
Coordinate Reference Frames v 2 D Cartesian Reference Frames x y y x 19 Korea University Computer Graphics

2 D Polar Coordinate Reference Frame 20 Korea University Computer Graphics

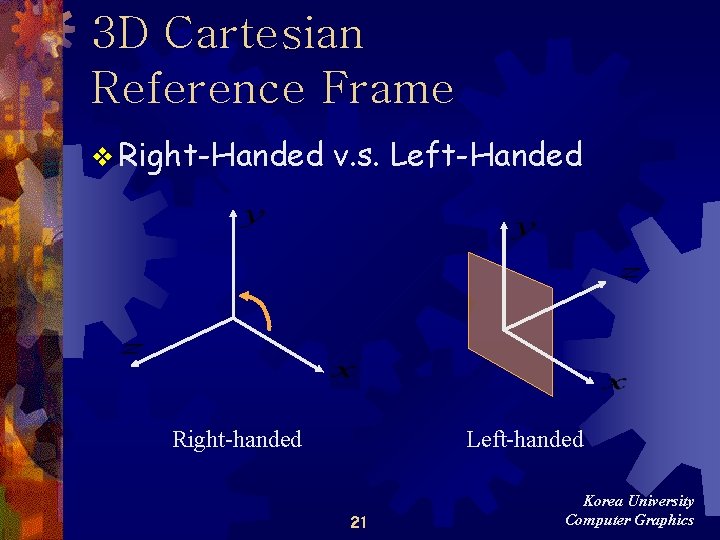
3 D Cartesian Reference Frame v Right-Handed v. s. Left-Handed Right-handed Left-handed 21 Korea University Computer Graphics

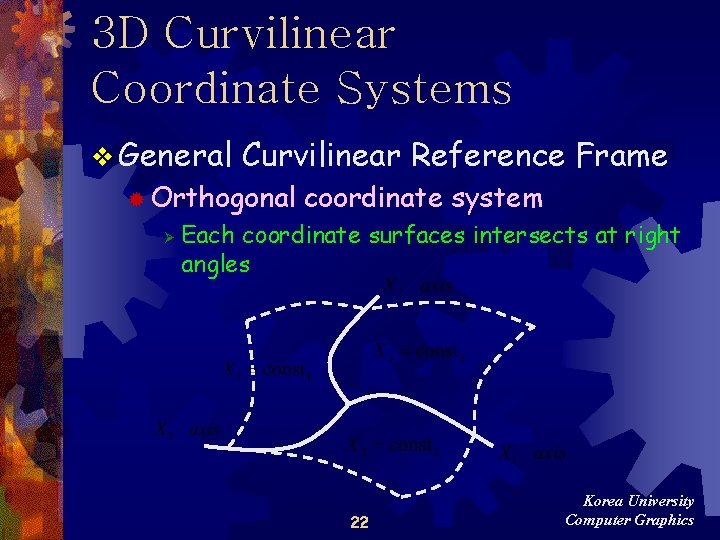
3 D Curvilinear Coordinate Systems v General Curvilinear Reference Frame ® Orthogonal Ø coordinate system Each coordinate surfaces intersects at right angles 22 Korea University Computer Graphics

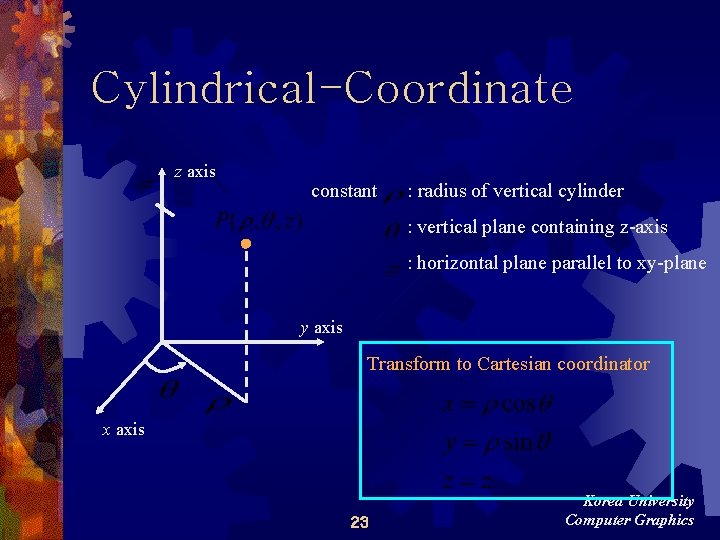
Cylindrical-Coordinate z axis constant : radius of vertical cylinder : vertical plane containing z-axis : horizontal plane parallel to xy-plane y axis Transform to Cartesian coordinator x axis 23 Korea University Computer Graphics

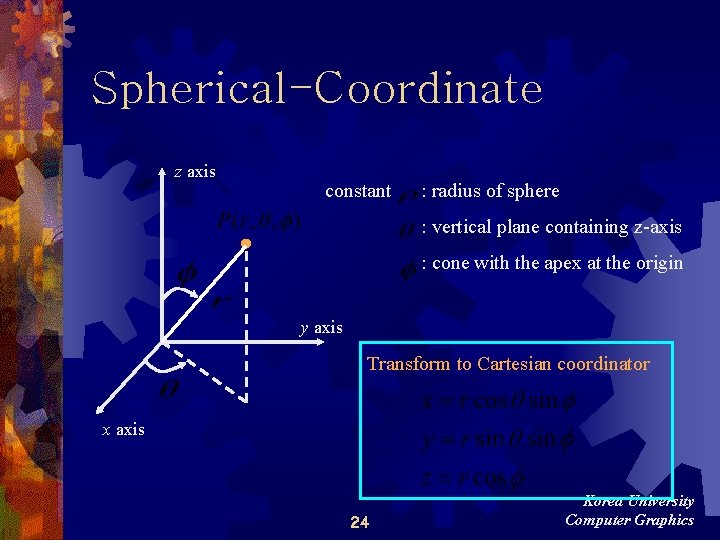
Spherical-Coordinate z axis constant : radius of sphere : vertical plane containing z-axis : cone with the apex at the origin y axis Transform to Cartesian coordinator x axis 24 Korea University Computer Graphics

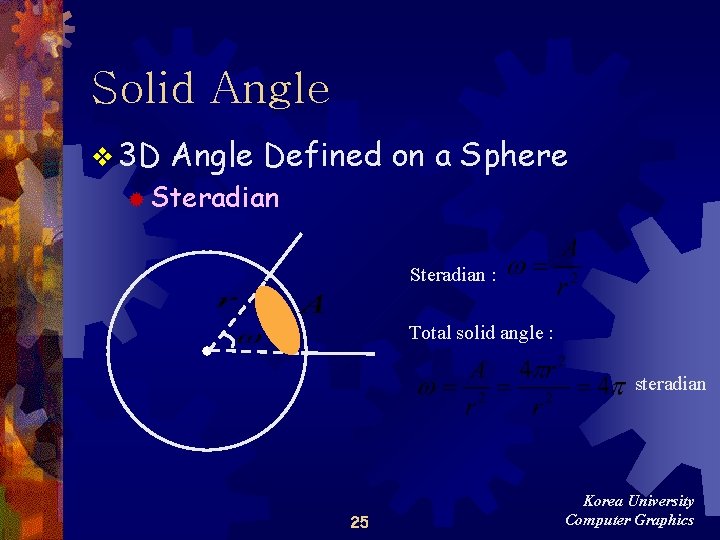
Solid Angle v 3 D Angle Defined on a Sphere ® Steradian : Total solid angle : steradian 25 Korea University Computer Graphics

Points & Vectors v Point ® Position in some reference frame ® Distance from the origin depends on the reference frame P y Frame B x 26 Frame A Korea University Computer Graphics

Points & Vectors (cont. ) v Vector ® Difference between two point positions ® Properties : Magnitude & direction Same properties within a single coordinate system Ø Magnitude is independent from coordinate frames Ø Magnitude : Direction : 27 Korea University Computer Graphics

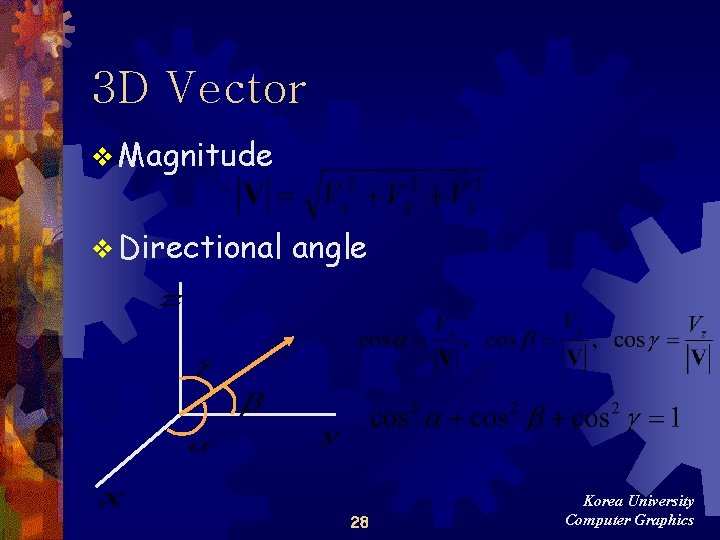
3 D Vector v Magnitude v Directional angle 28 Korea University Computer Graphics

Vector Addition & Scalar Multiplication v Addition v Scalar multiplication 29 Korea University Computer Graphics

Vector Multiplication v Scalar Product(Inner Product) Commutative : Distributive : Orthogonal : 30 Korea University Computer Graphics

Vector Multiplication (cont. ) v Vector Product(Cross Product) Noncommutative : Nonassociative : Distributive : Right-handed rule! 31 Korea University Computer Graphics