geometric method for solving equations Mesopotamia Persia Ancient

















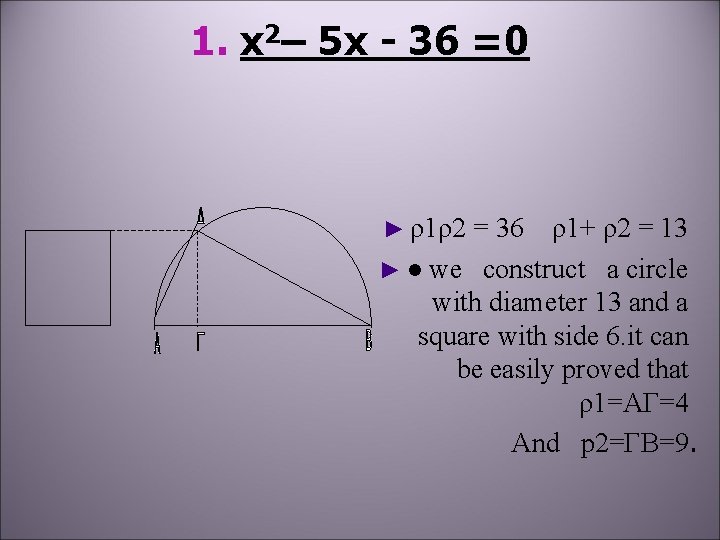




- Slides: 23

geometric method for solving equations Mesopotamia , Persia , Ancient Greece, China , European mathematicians

Generally… Nowadays , Geometric method for solving equations concerns solving equations and systems of equations using their graph…

►The Greeks created a geometric algebra where terms were represented by sides of geometric objects. Mathematicians of ancient China created calculating methods for solving equations and they applied them to geometric problems. The Arab mathematicians were able to interpret the results of certain cubic equations geometrically.

Persian – Arabian mathematicians… Omar Khayyam , Ibn al-Haytham , Sharaf al-Din al-Tusi , Ghiyath Al-Din Jamshid Al-Kashi…

Omar Khayyám (1048– 1122) ► He is well known for inventing the general method of solving cubic equations by intersecting a parabola with a circle. He also combined the use of trigonometry and approximation theory to provide methods of solving algebraic equations by geometrical means. He also solved the cubic equation x 3 + 200 x = 20 x 2 + 2000 by considering the intersection of a rectangular hyperbola and a circle.


Ibn al-Haytham (Alhazen) (945 -1040) This mathematician was able to solve by purely algebraic means certain cubic equations, and then to interpret the results geometrically.


Sharaf al-Din al-Tusi (1135 -1213) He used an algebraic method similar to Newton’s method.

Ghiyath Al-Din Jamshid Al-Kashi (13801429) ► In The Treatise on the Chord and Sine, al-Kashi computed sin 1° to nearly as much accuracy as his value for π. He also improved the method that his ancestor Sharaf al-Dīn al-Tūsī used. In algebra and numerical analysis, he developed an iterative method for solving cubic equations In order to determine sin 1°, al-Kashi discovered the following formula often attributed to François Viète in the 16 th century:


Chinese mathematicians… Qin Jioushao , Yang Hui , Liu Hui…

Qin Jiushao (1202 - 1261) ►. He wrote the mathematical treatise Shushu Jiuzhang (Mathematical Treatise in Nine Sections). In the treatise gives an equation whose coefficients are variables and Heron's formula for the area of a triangle.

Yang Hui (about 1238 - about 1298). ► In his works he described multiplication, division, root-extraction, quadratic and simultaneous equations, series, computations of areas of a rectangle, a trapezium, a circle, and other figures. He also gave a wonderful account of magic squares and magic circles.

Liu Hui (3 rd century) ► He found approximations to π using regular polygons with 3 × 2 n sides drawn in a circle. . Liu also wrote Haidao suanjing or Sea Island Mathematical Manual article. In it Liu uses Pythagoras's theorem to calculate heights of objects and distances to objects which cannot be measured directly.

A proof of the pythagorean theorem by liu hui

Greek mathematicians… Methods Euclides used to solve equations…
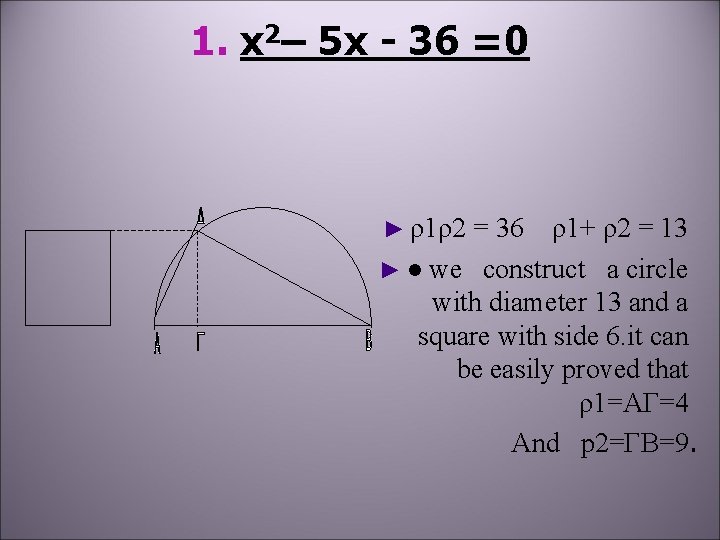
1. x 2– 5 x - 36 =0 ► ρ1ρ2 = 36 ρ1+ ρ2 = 13 ► ● we construct a circle with diameter 13 and a square with side 6. it can be easily proved that ρ1=AΓ=4 And p 2=ΓΒ=9.

2. x 2 – 5 x - 36 =0 ► the one radical x 1 is negative ρ1 =- Ιρ1Ι ► the other radical x 2 is positive ρ2= Ιρ2Ι ► we construct a circle of semi diameter 5. in a coincidental point we construct a geometric tangent ΑΓ=6. We adject point Γ with ► the centre of the circle. The half -line cuts the circle at points Α & Δ. ► For the two radicals it will be: Ιρ1Ι= ΓΒ = 4 Ιρ2Ι = ΓΔ = 9 ρ1= - 4 ρ2 = 9 ►

European mathematicians ► Techniques of applying geometrical constructions to algebraic problems were also adopted by a number of Renaissance mathematicians such as Gerolamo Cardano and Niccolò Fontana "Tartaglia" on their studies of the cubic equation. The geometrical approach to construction problems, rather than the algebraic one, was favoured by most 16 th and 17 th century mathematicians, notably Blaise Pascal. The French mathematicians Francisco Vieta and later René Descartes and Pierre de Fermat started the conventional way of thinking about construction problems through the introduction of coordinate geometry. They were interested primarily in the properties of algebraic curves, such as those defined by Diophantine equations (in the case of Fermat), and the algebraic reformulation of the classical Greek works on conics and cubics (in the case of Descartes).

Nowadays…

solve the quadratic equation : x² – ax + b sing a ruler and compasses only. first of all, we cannot solve the equation if the numbers a & b are not >1. ► Secondly, we make the points Y&Z have coordinates (0, 1)and (a , b) respectively. ► ► ► ► Method 1. Find the centre of the circle by finding the centre of YZ. 2. Using the compasses, draw the circle with diameter YZ. 3. the circle at the x-axis, creates the points x 1[with coordinates(x 1, 0)] and thepointx 2[with coordinates(x 2, 0)]. These are the roots of the equation x ² ax + b = 0 ►Although this method is really simple , we have to be really accurate when constructing the circle.

Thank you all. . ► Maria Chantzopoulou 3 rd general lyceum of karditsa