Geometric Mean We can visualize the geometric mean








- Slides: 11

Geometric Mean • We can visualize the geometric mean in two ways. Here is the first way: • Suppose we have two numbers a and b. What is the geometric mean of these two numbers ? • The geometric mean of a and b is the length of the side of a square who area is equal to the area of a rectangle with sides a and b. a b

Huntington-Hill Method • To determine how to round q, we must calculate the geometric mean of each state’s upper and lower quota. If q is less than this geometric mean, we round down. If q is equal or greater than the geometric mean, we round up. • Let q* represent the geometric mean of the upper and lower quota of q. That is, • We define << q >> to be the result of rounding q using the geometric mean. • Thus

Huntington-Hill Method • Back to the Huntington-Hill Method … • First, we calculate the standard divisor. Then we calculate q, the initial apportionment for each state. • Next, we round q using the geometric mean method. • Then, we determine if seats must be added or removed to result in the desired apportionment. • If seats must be added or removed, we must choose a modified divisor, as in the Jefferson and Webster method, so that rounding the resulting quotas by the geometric-mean method will produce the required total.

Example: Huntington-Hill Method • Let’s use the fictional country from a previous example. Suppose this country has states A, B and C with populations as given in the table below. Suppose the house size is 75 seats. State population A 453 B 367 C 697 total 1517

Example: Huntington-Hill Method • Let’s use the fictional country from a previous example. Suppose this country has states A, B and C with populations as given in the table below. Suppose the house size is 75 seats. State population A 453 B 367 C 697 total 1517 We calculate the standard divisor first… In this case, s = p/h = 1517/75 = 20. 2267

Example: Huntington-Hill Method • Let’s use the fictional country from a previous example. Suppose this country has states A, B and C with populations as given in the table below. Suppose the house size is 75 seats. State population q A 453/s = 22. 3962 B 367/s = 18. 1444 C 697/s = 34. 4595 total 1517 75 We must calculate the standard divisor first. In this case, s = p/h=1517/75 = 20. 2267 Now we can calculate the quota for each state … q = pi/s

Example: Huntington-Hill Method • Here, we are calculating q*, which is the geometric mean of the upper and lower quota for each state. State population q A 453/s = 22. 3962 B 367/s = 18. 1444 C 697/s = 34. 4595 total 1517 75 q*

Example: Huntington-Hill Method • Let’s use the fictional country from a previous example. Suppose this country has states A, B and C with populations as given in the table below. Suppose the house size is 75 seats. State population q q* A 453/s = 22. 3962 22. 4944 B 367/s = 18. 1444 18. 4932 C 697/s = 34. 4595 34. 4963 total 1517 75

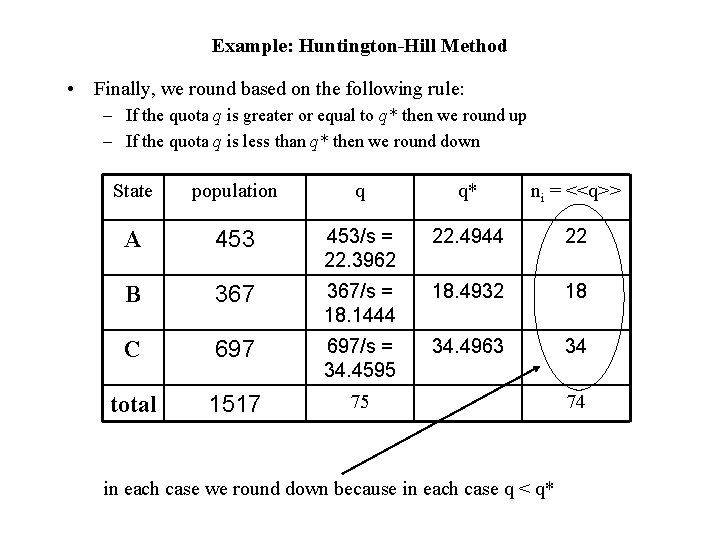
Example: Huntington-Hill Method • Finally, we round based on the following rule: – If the quota q is greater or equal to q* then we round up – If the quota q is less than q* then we round down State population q q* ni = <<q>> A 453/s = 22. 3962 22. 4944 22 B 367/s = 18. 1444 18. 4932 18 C 697/s = 34. 4595 34. 4963 34 total 1517 75 in each case we round down because in each case q < q* 74

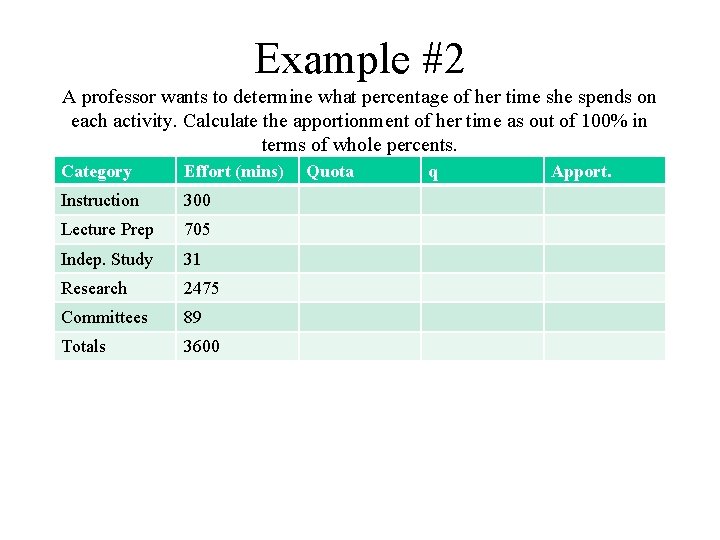
Example #2 A professor wants to determine what percentage of her time she spends on each activity. Calculate the apportionment of her time as out of 100% in terms of whole percents. Category Effort (mins) Instruction 300 Lecture Prep 705 Indep. Study 31 Research 2475 Committees 89 Totals 3600 Quota q Apport.

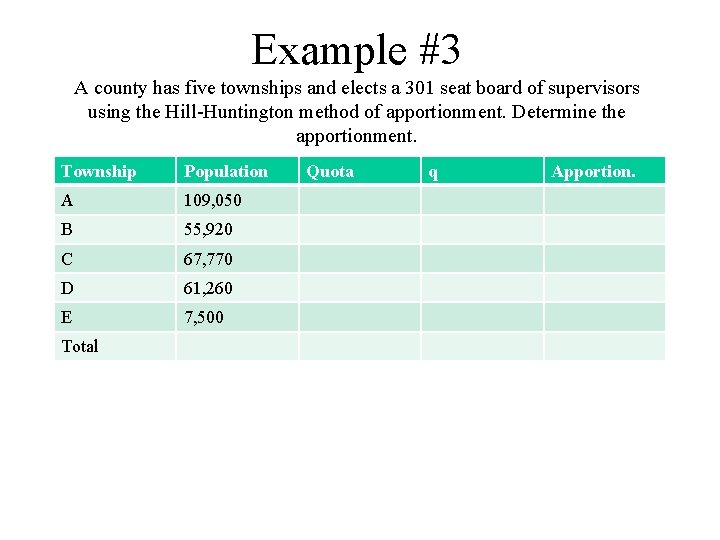
Example #3 A county has five townships and elects a 301 seat board of supervisors using the Hill-Huntington method of apportionment. Determine the apportionment. Township Population A 109, 050 B 55, 920 C 67, 770 D 61, 260 E 7, 500 Total Quota q Apportion.