GEOMETRIC DESIGN VERTICAL ALIGNMENT CE 331 Transportation Engineering

GEOMETRIC DESIGN: VERTICAL ALIGNMENT CE 331 Transportation Engineering

Objectives Describe components of vertical alignment ¢ Understand the design criteria for vertical curve ¢ Determine the minimum length of a vertical curve ¢ Calculate the stations and elevations along a vertical curve ¢ Slide 2

Vertical Alignment ¢ Components l Tangent grade • AASHTO guideline recommends maximum grades l Vertical curve • Minimum length (Lmin) • Stations and elevations of points along the curve Slide 3

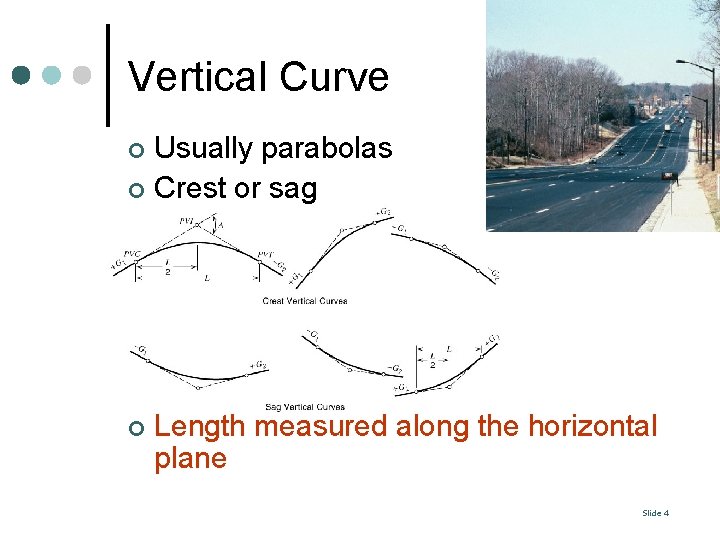
Vertical Curve Usually parabolas ¢ Crest or sag ¢ ¢ Length measured along the horizontal plane Slide 4

Assistant with Target Rod (2 ft object height) Observer with Sighting Rod (3. 5 ft) 5 Slide 5

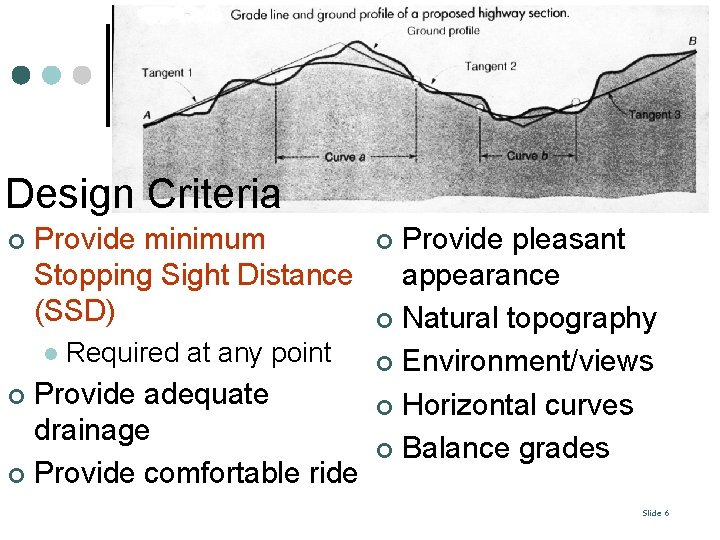
Design Criteria ¢ Provide minimum Stopping Sight Distance (SSD) l Required at any point Provide adequate drainage ¢ Provide comfortable ride ¢ Provide pleasant appearance ¢ Natural topography ¢ Environment/views ¢ Horizontal curves ¢ Balance grades ¢ Slide 6

Minimum Length of the Vertical Curve (Lmin) – based on SSD requirement Crest Sag SSD<L A*SSD 2/2158 A*SSD 2/(400+3. 5 SSD) SSD>L 2 SSD – (2158/A) 2 SSD - (400 + 3. 5 SSD)/A A = |g 2 – g 1|*100 (%) SSD: Stopping Sight Distance (ft) Slide 7

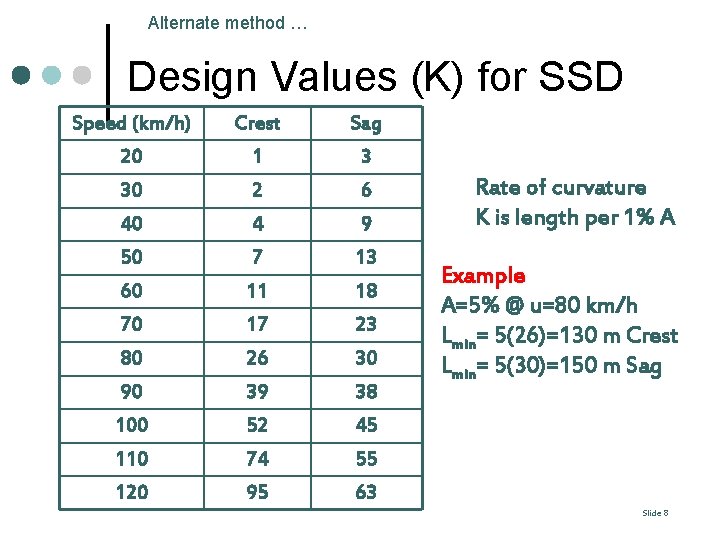
Alternate method … Design Values (K) for SSD Speed (km/h) Crest Sag 20 1 3 30 2 6 40 4 9 50 7 13 60 11 18 70 17 23 80 26 30 90 39 38 100 52 45 110 74 55 120 95 63 Rate of curvature K is length per 1% A Example A=5% @ u=80 km/h Lmin= 5(26)=130 m Crest Lmin= 5(30)=150 m Sag Slide 8

Example ¢ A vertical curve connects a 3% grade with a 0% grade. The required stopping sight distance is 440 ft. What should be the minimum length of the curve? Slide 9

Calculate Stations & Elevations ¢ End points Sta. PVC = Sta. PVI – L/2 l HPVC = HPVI – g 1·L/2 l Sta. PVT = Sta. PVI + L/2 l HPVT = HPVI + g 2·L/2 l ¢ Other points Define a coordinate system (next slide) l Find H for each x (usually in 100 ft increment) l Slide 10

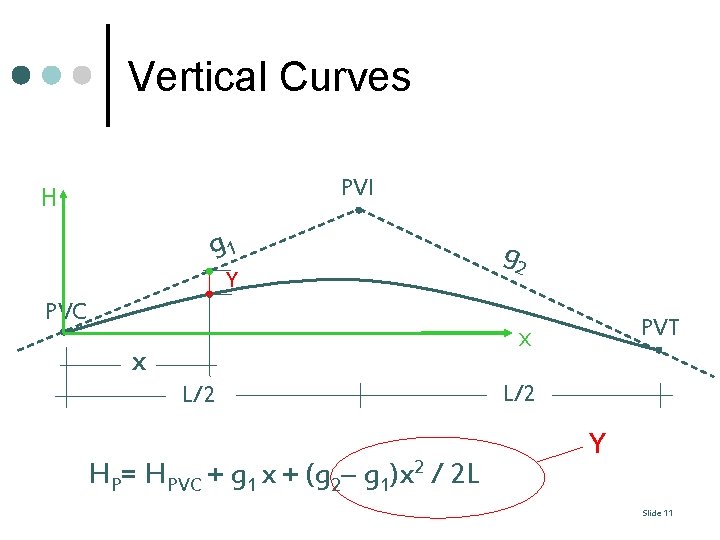
Vertical Curves PVI H g 1 Y PVC g 2 PVT x x L/2 HP= HPVC + g 1 x + (g 2– g 1)x 2 / 2 L L/2 Y Slide 11

Examples ¢ Two types of design problems Unconstrained l Constrained l • Passing through certain point, or • Maintaining certain clearance from object Slide 12

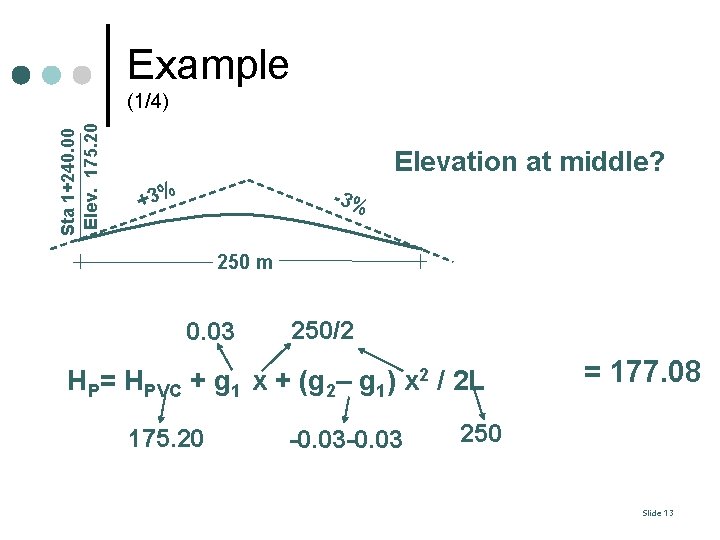
Example Sta 1+240. 00 Elev. 175. 20 (1/4) Elevation at middle? +3% -3% 250 m 0. 03 250/2 HP= HPVC + g 1 x + (g 2– g 1) x 2 / 2 L 175. 20 -0. 03 = 177. 08 250 Slide 13

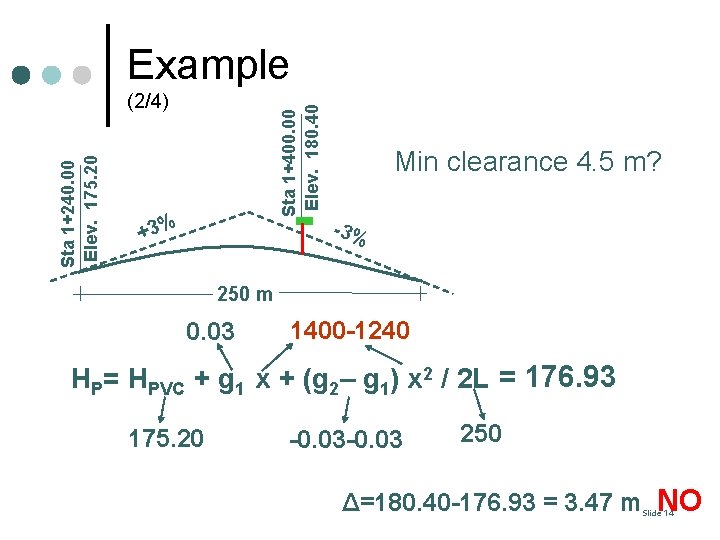
Example Sta 1+400. 00 Elev. 180. 40 Sta 1+240. 00 Elev. 175. 20 (2/4) +3% Min clearance 4. 5 m? -3% 250 m 0. 03 1400 -1240 HP= HPVC + g 1 x + (g 2– g 1) x 2 / 2 L = 176. 93 175. 20 -0. 03 250 Δ=180. 40 -176. 93 = 3. 47 m NO Slide 14

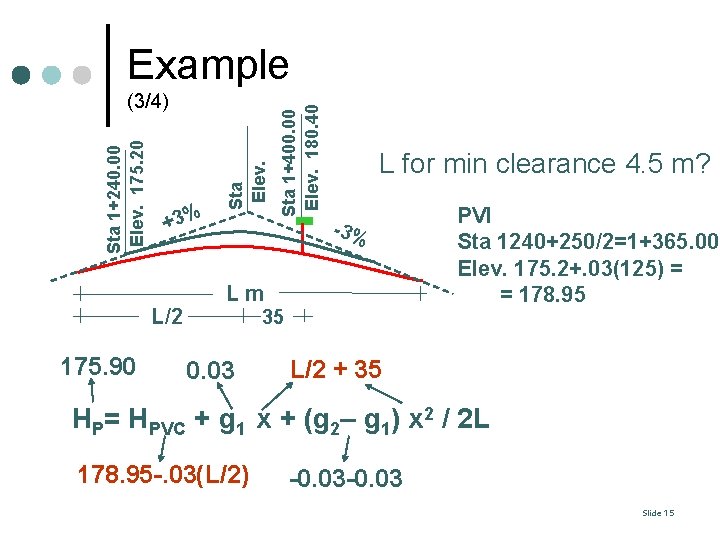
+3% L/2 175. 90 Sta Elev. Sta 1+240. 00 Elev. 175. 20 (3/4) Sta 1+400. 00 Elev. 180. 40 Example L for min clearance 4. 5 m? -3% Lm 35 0. 03 PVI Sta 1240+250/2=1+365. 00 Elev. 175. 2+. 03(125) = = 178. 95 L/2 + 35 HP= HPVC + g 1 x + (g 2– g 1) x 2 / 2 L 178. 95 -. 03(L/2) -0. 03 Slide 15

Example (4/4) 175. 90 = [178. 95 -0. 03(L/2)]+[0. 03(L/2+35)]+ +[(-0. 03)(L/2+35)2/2 L] 175. 90 -178. 95 -0. 03(35)= -0. 06(L/2+35)2/2 L -4. 1= -0. 06(L/2+35)2/2 L 136. 67 L =(L/2+35)2 136. 67 L=L 2/4+2(L/2)(35)+352 L 2 -406. 67 L+4900=0 L 1 = 12. 43 m L 2 =394. 24 m Slide 16