GEOMETRIC DESIGN HORIZONTAL ALIGNMENT CE 331 Transportation Engineering

Objectives Describe components of horizontal alignment ¢ Determine design parameters for circular curve ¢

General Concepts ¢ Components Tangents l Curves (circular) l ¢ Design values l Function

Horizontal Curves PI Δ π R Δ/180 Arc L= Cord C = 2 R

30 o Sta 7+75 T L Given: R = 1800 ft, Δ = 30

Example A highway has a design speed of 70 mph and a superelevation rate

Example (cont’d) If the curve is fitted through two tangents with central angle Δ

Sight Distance on Horizontal Curves ¢ Clearance from roadside obstruction M’ measured from the

Example Min. distance to wall from centerline to ensure SSD? M’ CL Given: R=1000

Example (cont’d) M’ CL What if the clearance from the centerline is 35 ft?

Deflection Angles ¢ ¢ Used in laying out curves Incremental central angle δi =

(1/4) Sta 1+556. 91 Example R = 600 m Deflection angles, cords? PC Sta

Laying Out a Curve (2/4) PC θ 2 θ 3 1+500. 00 θ 1

Example (3/4) ¢ 1 st Station 1400 -1396. 14 = 3. 86 m l

Curve Layout Data Station 1+396. 14 1+400. 00 1+450. 00 1+500. 00 1+550. 00

¢ Used to help surveyors stakeout curve Arc -> Roadways Chord -> Railroads

Superelevation Pavement cross slope to keep vehicles on road ¢ e + fs =

Superelevation Issues emax – Lower in Maine than in Florida – Why? ¢ fs

Superelevation Transition To From ¢ Tangent Runout w Superelevation 2% 0% Runoff w Pavement

Superelevation Transition PC 0% e% A 2% Example W = 3. 30 m TR

Where do we rotate the roadway? ¢ Rotate pavement about the centerline most common

How do we transition into a super-elevated curve? ¢ No Spiral ¢ Spiral

Slides: 44

Download presentation

GEOMETRIC DESIGN: HORIZONTAL ALIGNMENT CE 331 Transportation Engineering

Objectives Describe components of horizontal alignment ¢ Determine design parameters for circular curve ¢ Understand the impact of superelevation and stopping sight distance on the design of horizontal curve ¢ 2

General Concepts ¢ Components Tangents l Curves (circular) l ¢ Design values l Function of design speed and superelevation Stopping sight distance at any point ¢ Length measured along centerline of 3 the curve ¢

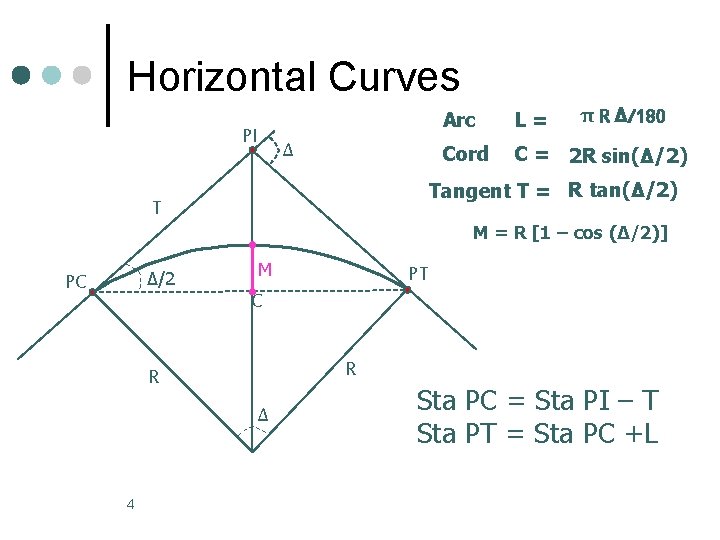
Horizontal Curves PI Δ π R Δ/180 Arc L= Cord C = 2 R sin(Δ/2) Tangent T = R tan(Δ/2) T M = R [1 – cos (Δ/2)] Δ/2 PC M PT C R R Δ 4 Sta PC = Sta PI – T Sta PT = Sta PC +L

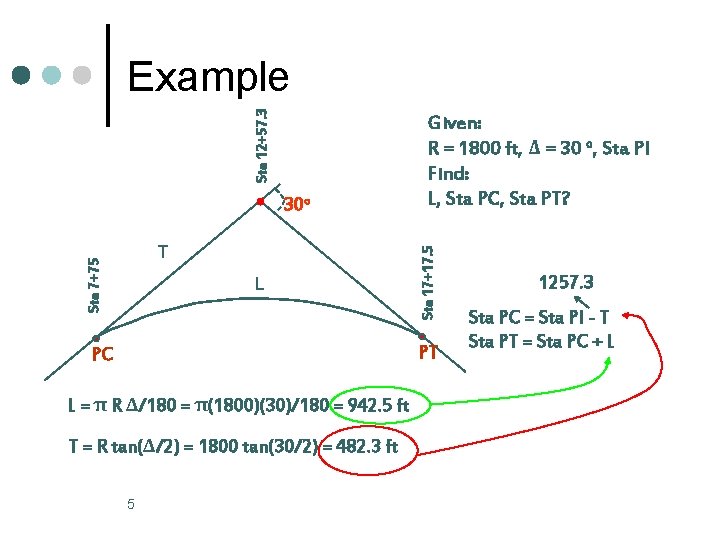
30 o Sta 7+75 T L Given: R = 1800 ft, Δ = 30 o, Sta PI Find: L, Sta PC, Sta PT? Sta 17+17. 5 Sta 12+57. 3 Example PT PC L = π R Δ/180 = π(1800)(30)/180 = 942. 5 ft T = R tan(Δ/2) = 1800 tan(30/2) = 482. 3 ft 5 1257. 3 Sta PC = Sta PI - T Sta PT = Sta PC + L

Example A highway has a design speed of 70 mph and a superelevation rate of 0. 01. If fs = 0. 15, What should be the radius of the curve? R = V 2/[15(fs+e)] = 702/[15*(0. 15+0. 01)] = 2042 (ft) 6

Example (cont’d) If the curve is fitted through two tangents with central angle Δ = 25°, How long should the curve be? L = πRΔ/180 = π*2042*25/180 = 891 (ft) 7

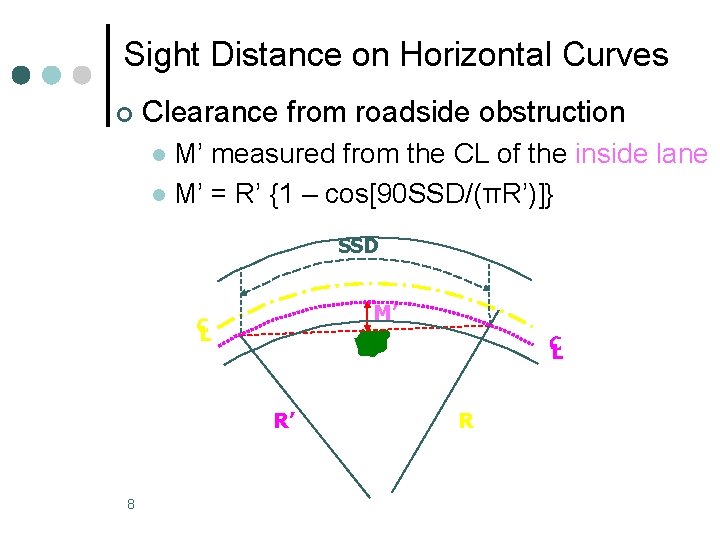
Sight Distance on Horizontal Curves ¢ Clearance from roadside obstruction M’ measured from the CL of the inside lane l M’ = R’ {1 – cos[90 SSD/(πR’)]} l SSD M’ CL CL R’ 8 R

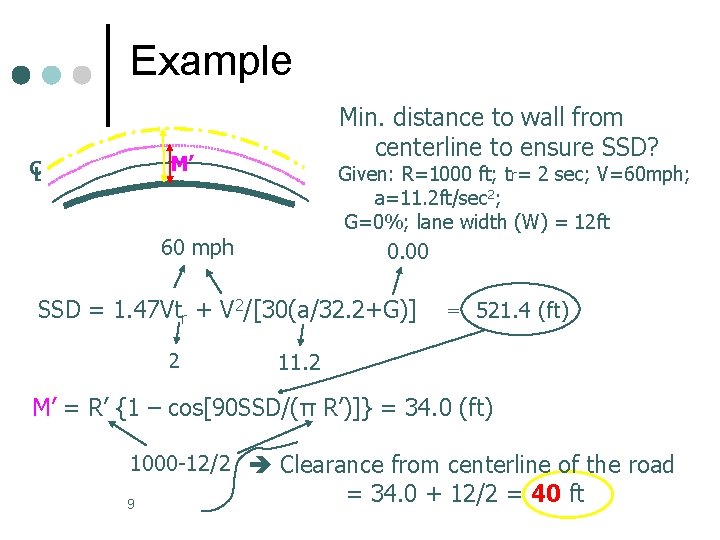
Example Min. distance to wall from centerline to ensure SSD? M’ CL Given: R=1000 ft; tr= 2 sec; V=60 mph; a=11. 2 ft/sec 2; G=0%; lane width (W) = 12 ft 60 mph 0. 00 SSD = 1. 47 Vtr + V 2/[30(a/32. 2+G)] 2 = 521. 4 (ft) 11. 2 M’ = R’ {1 – cos[90 SSD/(π R’)]} = 34. 0 (ft) 1000 -12/2 Clearance from centerline of the road 9 = 34. 0 + 12/2 = 40 ft

Example (cont’d) M’ CL What if the clearance from the centerline is 35 ft? Change V. M’ = 35 – 12/2 = 29 ft Find SSD associated with M’: M’ = R’ {1 – cos[90 SSD/(π R’)]} SSD = πR’ cos-1(1 - M’/R’)/90 = 481. 4 (ft) SSD = 1. 47 Vtr + V 2/[30(a/32. 2+G)] V = 57. 1 (mph) Speed limit = 55 mph 10

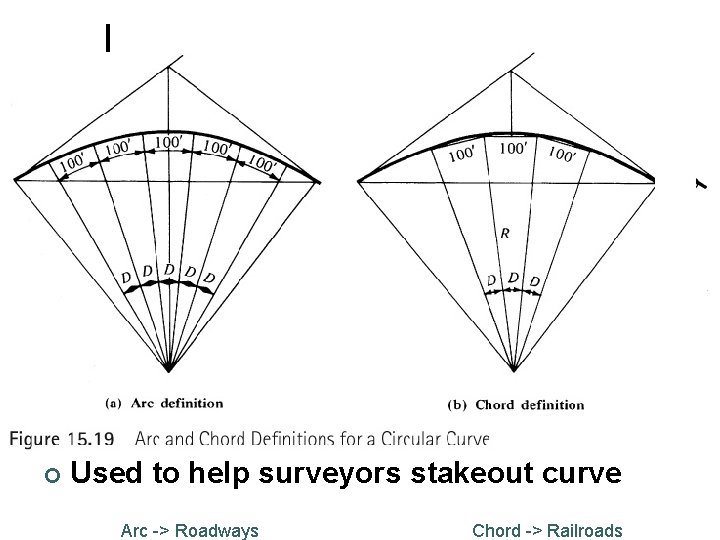
Deflection Angles ¢ ¢ Used in laying out curves Incremental central angle δi = 180 xi /(Rπ) Subtended angles θi = δi/2=180 xi /(2 Rπ) Deflection angles l ¢ Cumulative of subtended angles Chords for laying out curve l Ci = 2 R sin(δi/2) = 2 R sin(θi)

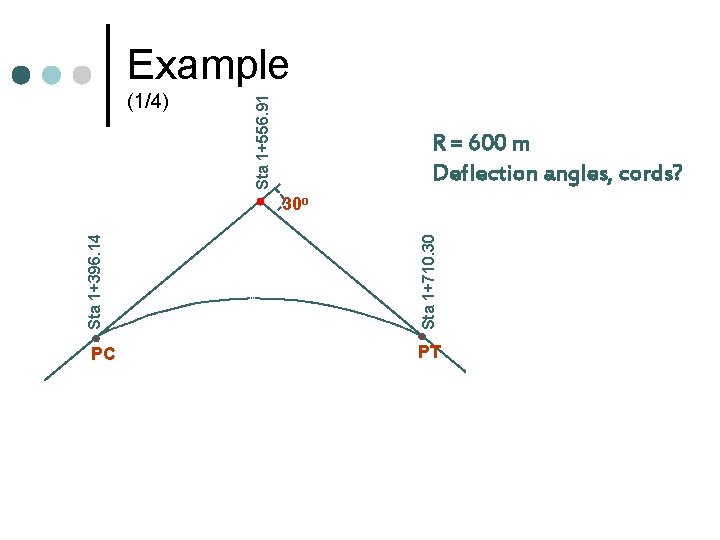
(1/4) Sta 1+556. 91 Example R = 600 m Deflection angles, cords? PC Sta 1+710. 30 Sta 1+396. 14 30 o PT

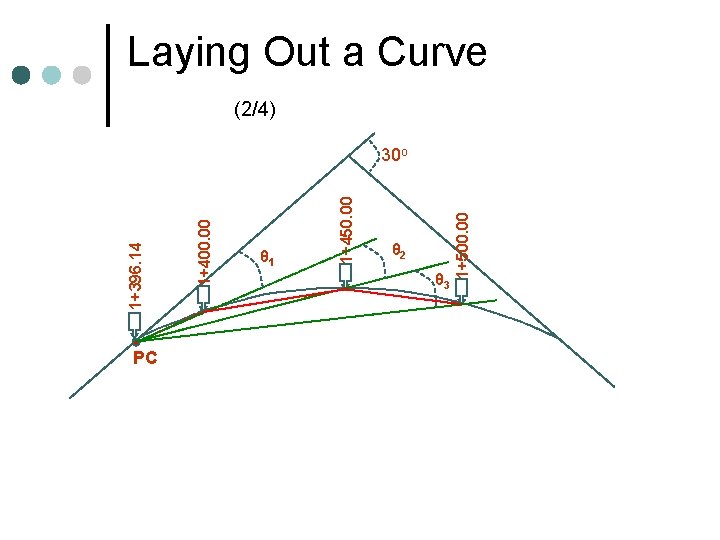
Laying Out a Curve (2/4) PC θ 2 θ 3 1+500. 00 θ 1 1+450. 00 1+400. 00 1+396. 14 30 o

Example (3/4) ¢ 1 st Station 1400 -1396. 14 = 3. 86 m l θ 1 = 180 (3. 86)/[2 (600) π] = 0. 18 o l C 1 = 2 (600)sin(0. 18) = 3. 86 m l ¢ 2 nd Station 1450 -1400 = 50. 00 m l θ 2 = 180 (50)/[2 (600) π] = 2. 39 o l C 2 = 2 (600)sin(2. 39) = 49. 99 m l

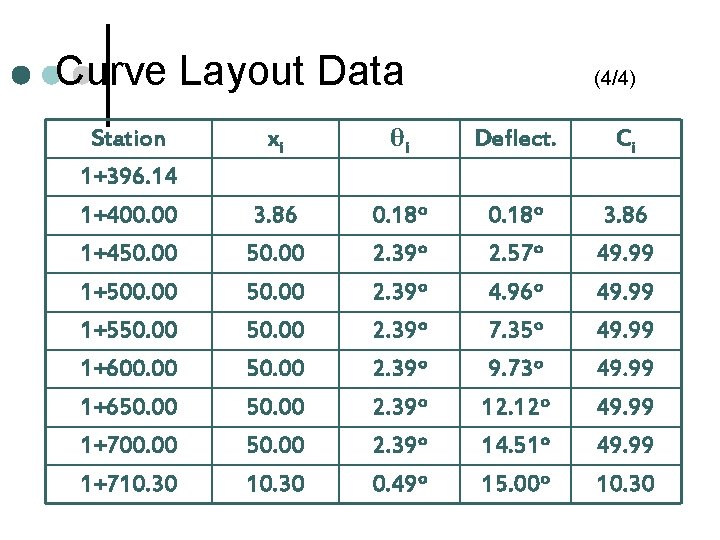
Curve Layout Data Station 1+396. 14 1+400. 00 1+450. 00 1+500. 00 1+550. 00 1+600. 00 1+650. 00 1+700. 00 1+710. 30 (4/4) xi θi Deflect. Ci 3. 86 50. 00 10. 30 0. 18 o 2. 39 o 0. 49 o 0. 18 o 2. 57 o 4. 96 o 7. 35 o 9. 73 o 12. 12 o 14. 51 o 15. 00 o 3. 86 49. 99 10. 30

¢ Used to help surveyors stakeout curve Arc -> Roadways Chord -> Railroads

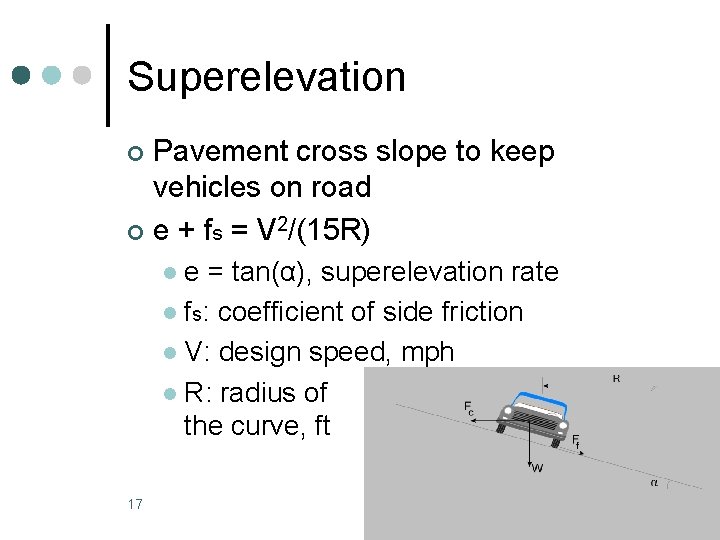
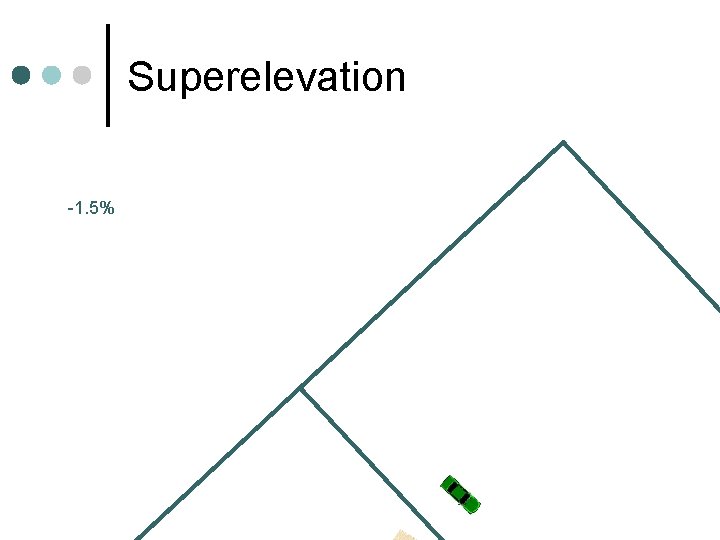
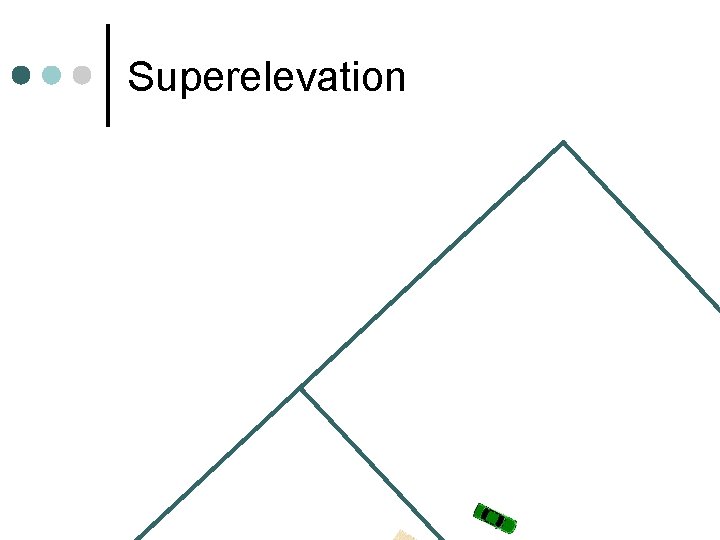
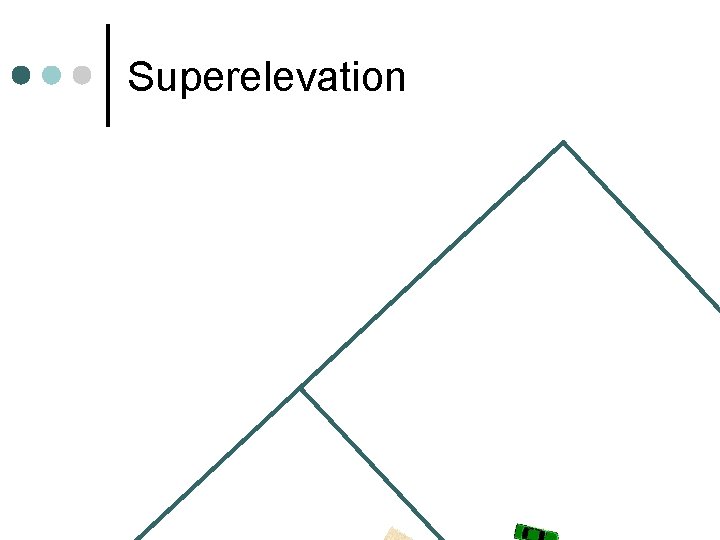
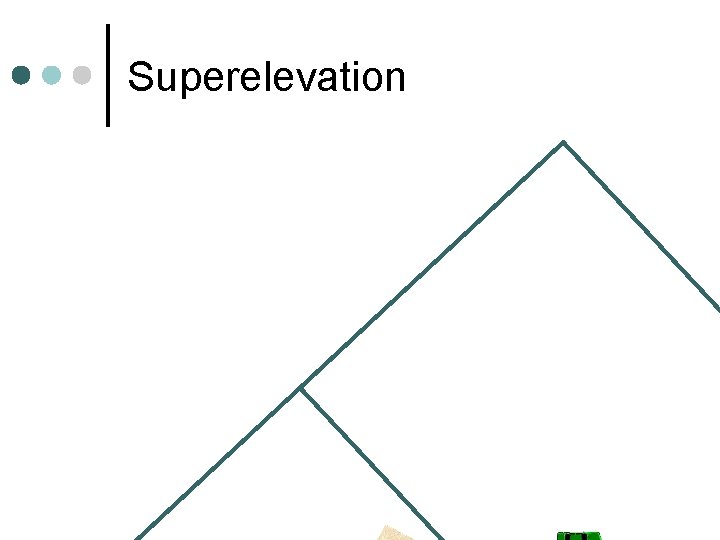
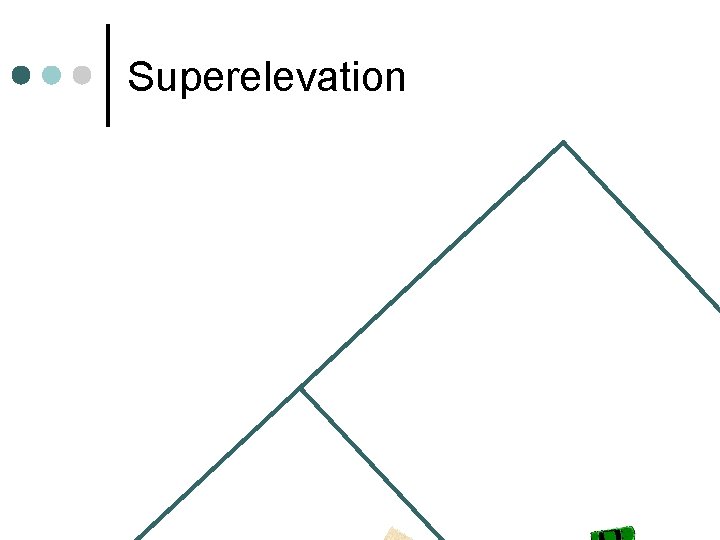
Superelevation Pavement cross slope to keep vehicles on road ¢ e + fs = V 2/(15 R) ¢ e = tan(α), superelevation rate l fs: coefficient of side friction l V: design speed, mph l R: radius of the curve, ft l 17

Superelevation Issues emax – Lower in Maine than in Florida – Why? ¢ fs is a function of driver comfort and safety ¢ l ranges from 0. 17 for 20 mph to 0. 08 at 80 mph Max superelevation sets Min radius ¢ Practice: AASHTO Green Book tables ¢ 18

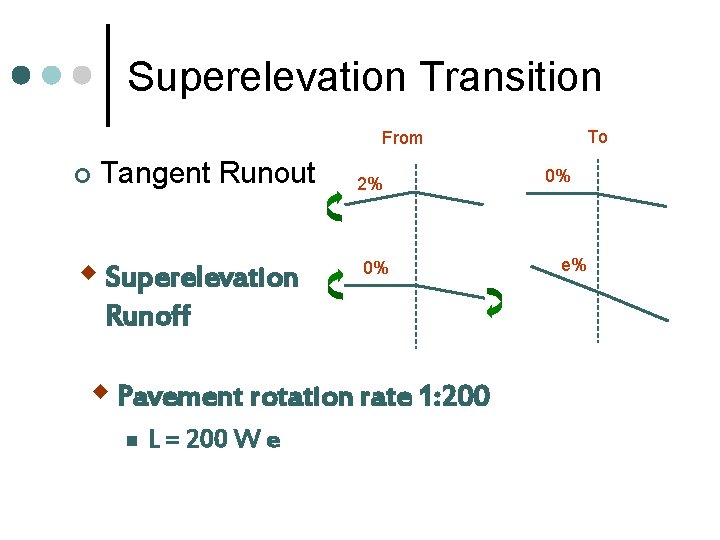
Superelevation Transition To From ¢ Tangent Runout w Superelevation 2% 0% Runoff w Pavement rotation rate 1: 200 n L = 200 W e 0% e%

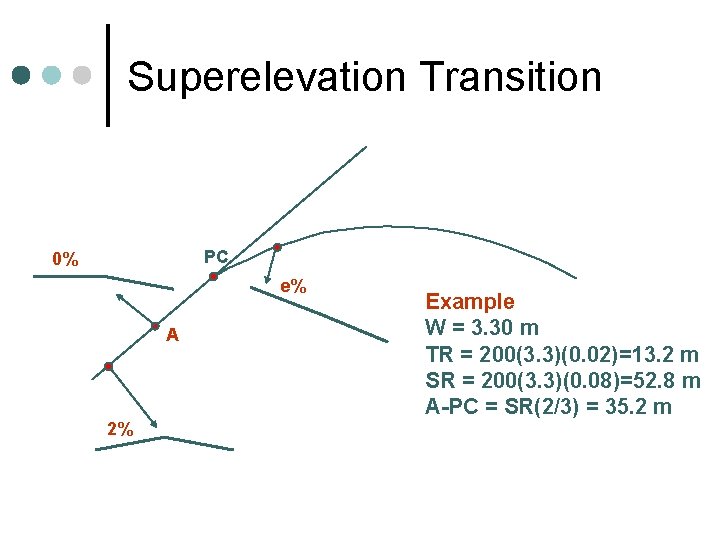
Superelevation Transition PC 0% e% A 2% Example W = 3. 30 m TR = 200(3. 3)(0. 02)=13. 2 m SR = 200(3. 3)(0. 08)=52. 8 m A-PC = SR(2/3) = 35. 2 m

Where do we rotate the roadway? ¢ Rotate pavement about the centerline most common for undivided roadways l Others mainly for drainage or terrain l Rotate pavement about the inner edge ¢ Rotate pavement about the outside edge ¢ Rotate about the center of the median ¢

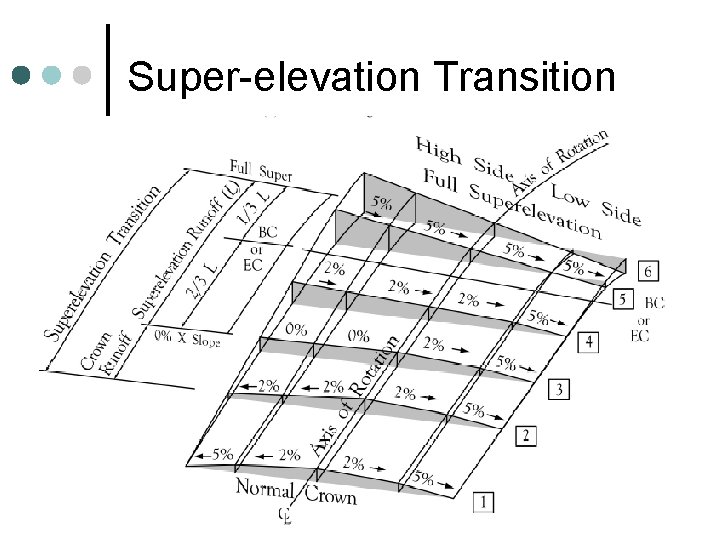
Super-elevation Transition

Superelevation

Superelevation -1. 5%

Superelevation

How do we transition into a super-elevated curve? ¢ No Spiral ¢ Spiral