Geometric Crossover for Multiway Graph Partitioning YongHyuk Kim

Geometric Crossover for Multiway Graph Partitioning Yong-Hyuk Kim, Yourim Yoon, Alberto Moraglio, and Byung-Ro Moon

Contents • Multiway graph partitioning • Geometric crossover – Hamming distance – Labeling-independent distance • Fitness landscape analysis • Experimental results • Conclusions

Multiway Graph Partitioning Problem

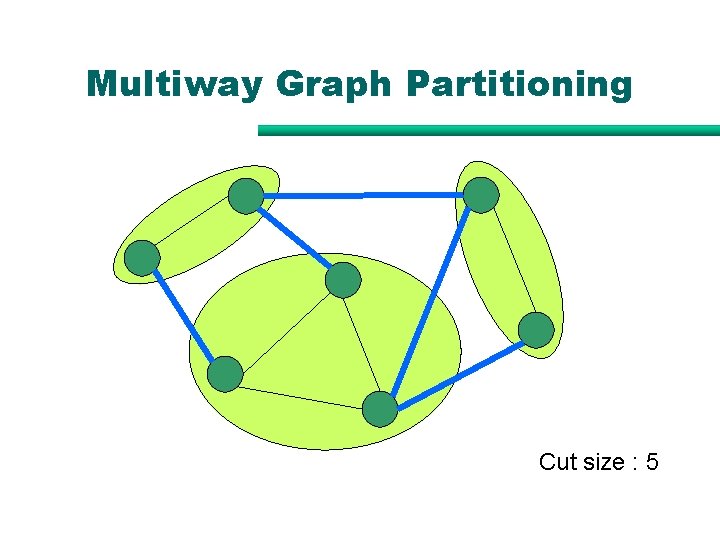
Multiway Graph Partitioning Cut size : 5

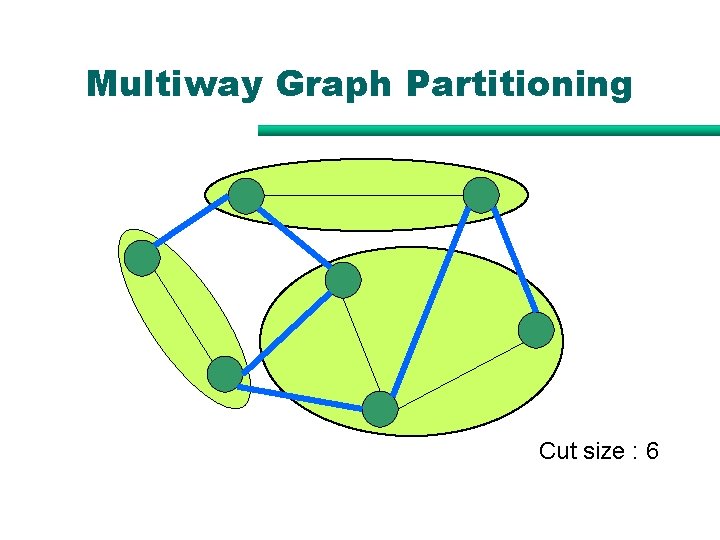
Multiway Graph Partitioning Cut size : 6

Geometric Crossover

Geometric Crossover • Line segment x y • A binary operator GX is a geometric crossover if all offspring are in a segment between its parents. • Geometric crossover is dependent on the metric.

Geometric Crossover • The traditional n-point crossover is geometric under the Hamming distance. 1 A 0 1 1 0 1 B 1 1 0 1 1 B X 2 3 A X 0 1 1 H(A, X) + H(X, B) = H(A, B)

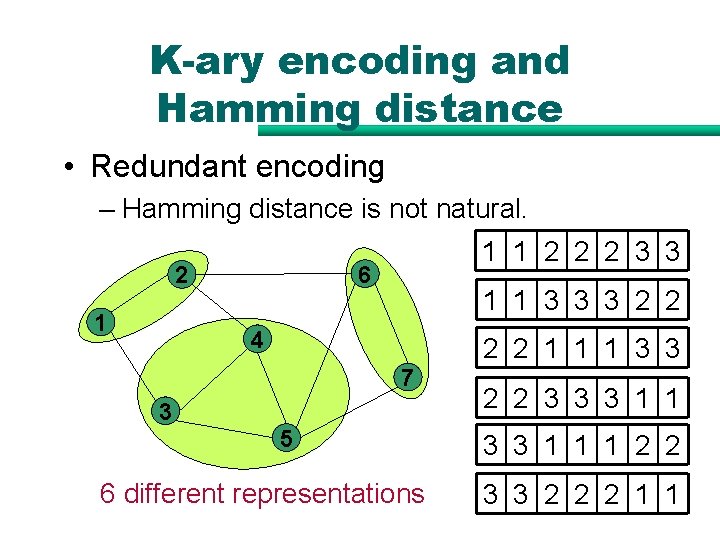
K-ary encoding and Hamming distance • Redundant encoding – Hamming distance is not natural. 6 2 1 1 1 2 2 2 3 3 1 1 3 3 3 2 2 4 2 2 1 1 1 3 3 7 3 5 6 different representations 2 2 3 3 3 1 1 1 2 2 3 3 2 2 2 1 1

Labeling-independent Distance • Given two K-ary encoding, and , , where is a metric. • If the metric is the Hamming distance H, LI can be computed efficiently by the Hungarian method.

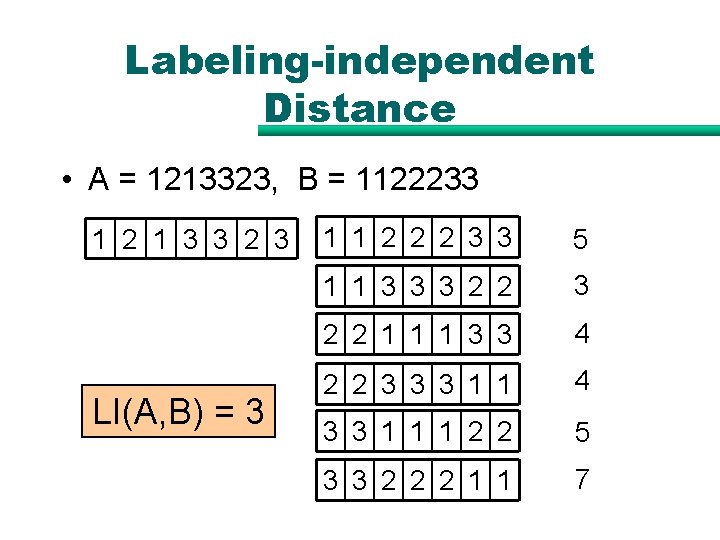
Labeling-independent Distance • A = 1213323, B = 1122233 1 2 1 3 3 2 3 LI(A, B) = 3 1 1 2 2 2 3 3 5 1 1 3 3 3 2 2 1 1 1 3 3 4 2 2 3 3 3 1 1 4 3 3 1 1 1 2 2 5 3 3 2 2 2 1 1 7

N-point LI-GX • Definition (N-point LI-GX) – Normalize the second parent to the first under the Hamming distance. Do the normal n-point crossover using the first parent and the normalized second parent. • The n-point LI-GX is geometric under the labeling-independent metric.

Fitness Landscape Analysis

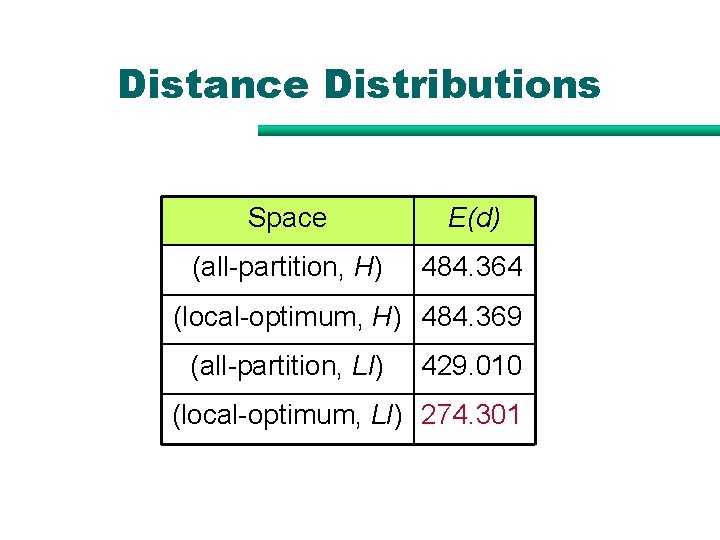
Distance Distributions Space E(d) (all-partition, H) 484. 364 (local-optimum, H) 484. 369 (all-partition, LI) 429. 010 (local-optimum, LI) 274. 301

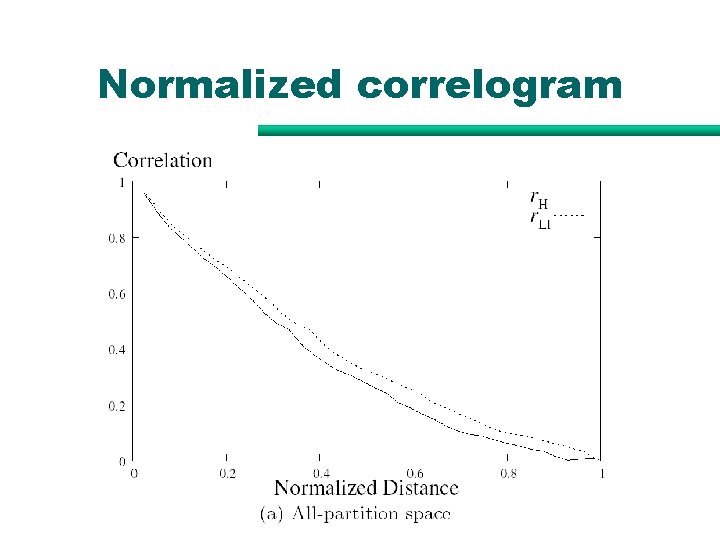
Normalized correlogram

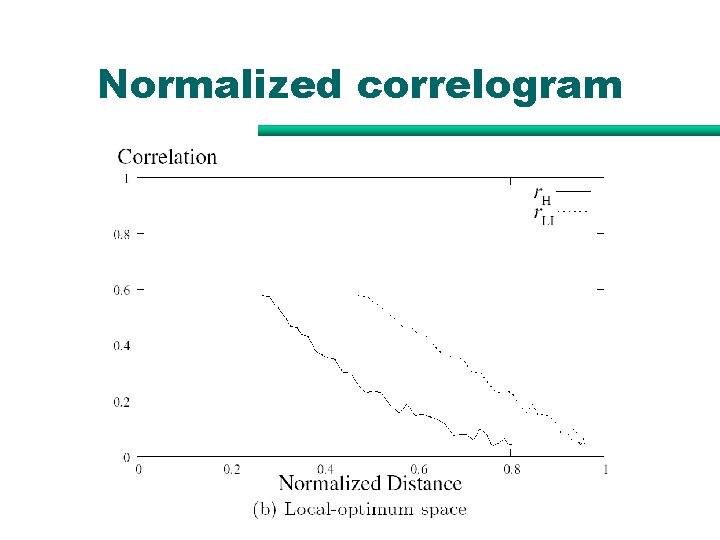
Normalized correlogram

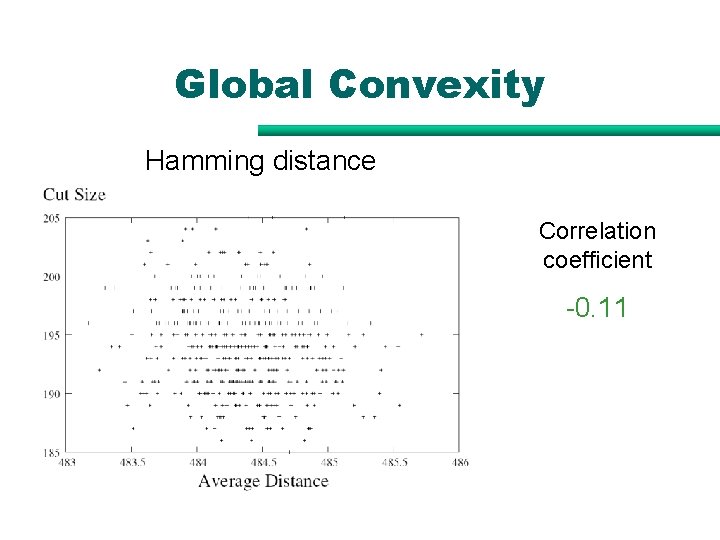
Global Convexity Hamming distance Correlation coefficient -0. 11

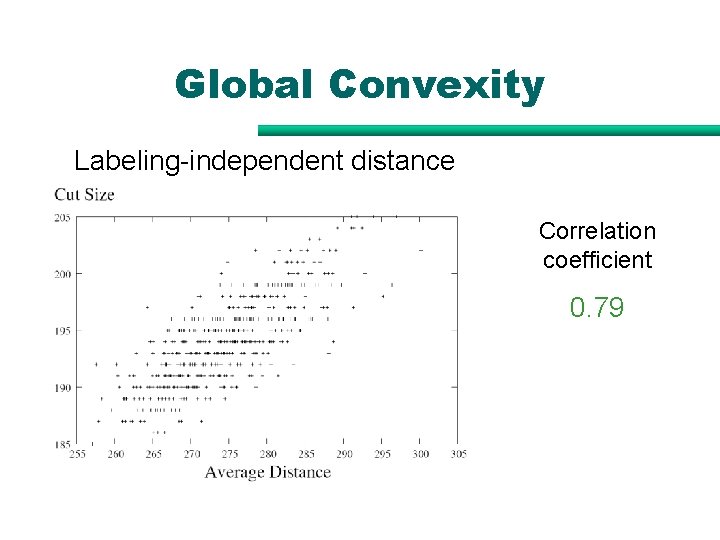
Global Convexity Labeling-independent distance Correlation coefficient 0. 79

Experimental Results

Genetic Framework • GA + FM variant • Population size : 50 • Selection – Roulette-wheel proportional selection • Replacement – Genitor-style replacement • Steady-state GA

Test Environment • Data Set – Johnson’s benchmark data – 4 random graphs (G*. *) and 4 random geometric graphs (U*. *) with 500 vertices. – Used in a number of other graphpartitioning studies. • Tests on 32 -way and 128 -way partitioning

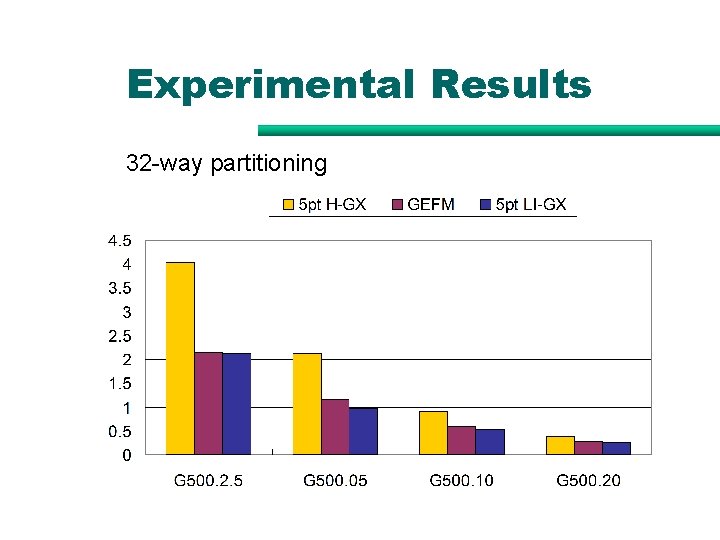
Experimental Results 32 -way partitioning

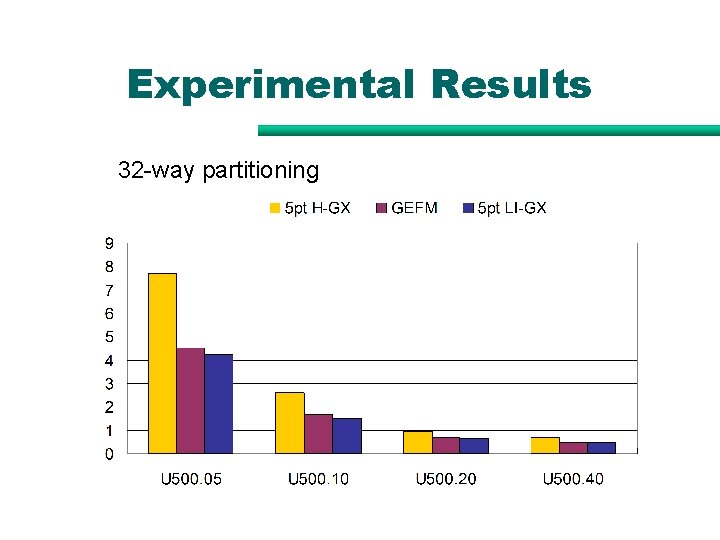
Experimental Results 32 -way partitioning

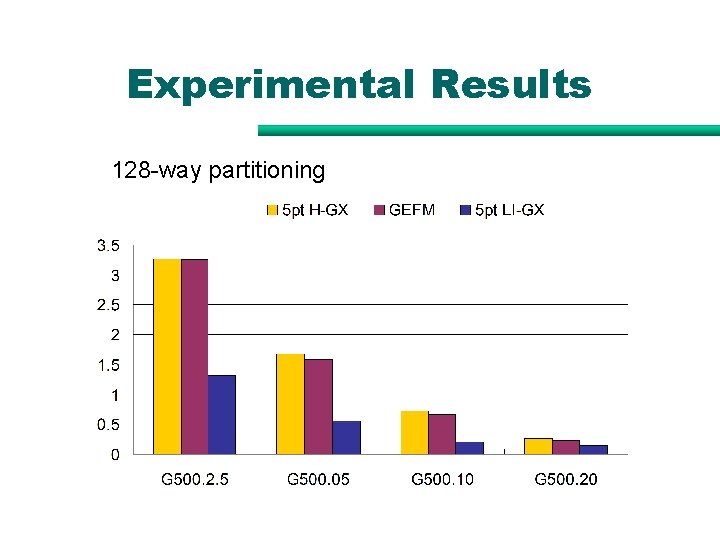
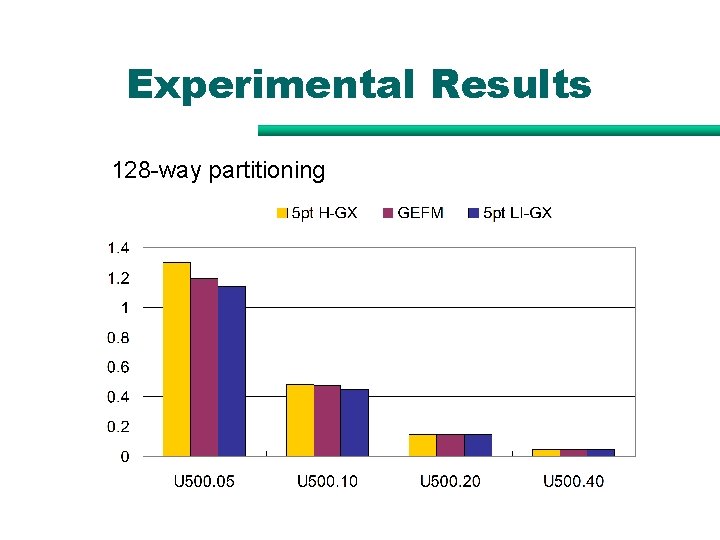
Experimental Results 128 -way partitioning

Experimental Results 128 -way partitioning

Conclusion • Methodology – Designed a geometric crossover based on the labeling independent distance. – Provided evidence for the fact that the labeling-independent distance is more suitable for the multiway graph partitioning problem by the fitness landscape analysis. • Performance – Performed better than existing genetic algorithms.