Geometric Constructions T Madas Constructing Midpoints Perpendicular Bisectors

Geometric Constructions © T Madas

Constructing Midpoints & Perpendicular Bisectors © T Madas

Constructing the Midpoint & Perpendicular bisector of a line segment Construction Lines C A B D Construction Lines © T Madas

Constructing Angle Bisectors © T Madas

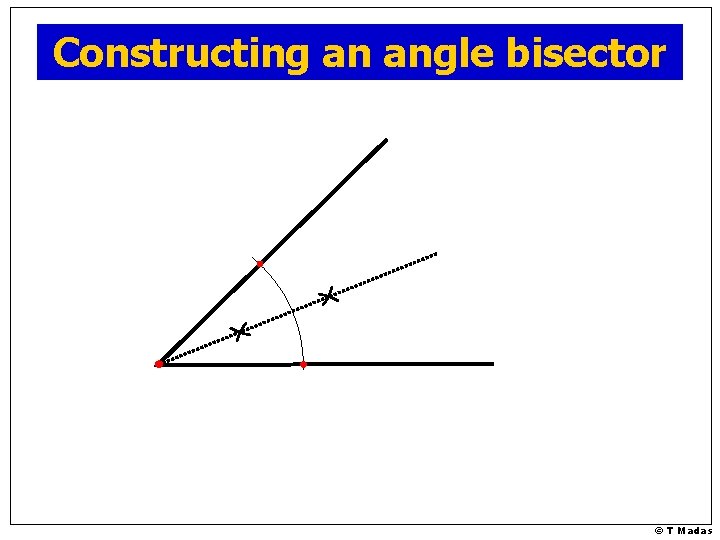
Constructing an angle bisector © T Madas

Constructing Equilateral Triangles © T Madas

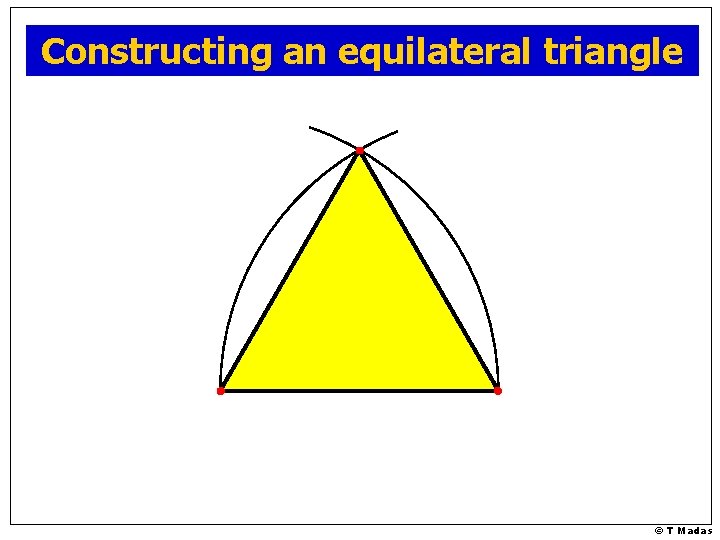
Constructing an equilateral triangle © T Madas

Constructing a perpendicular to a given point on a line © T Madas

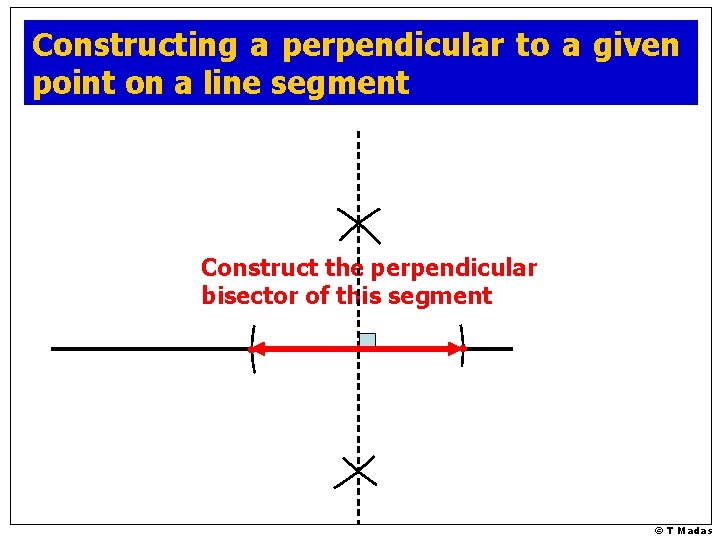
Constructing a perpendicular to a given point on a line segment Construct the perpendicular bisector of this segment © T Madas

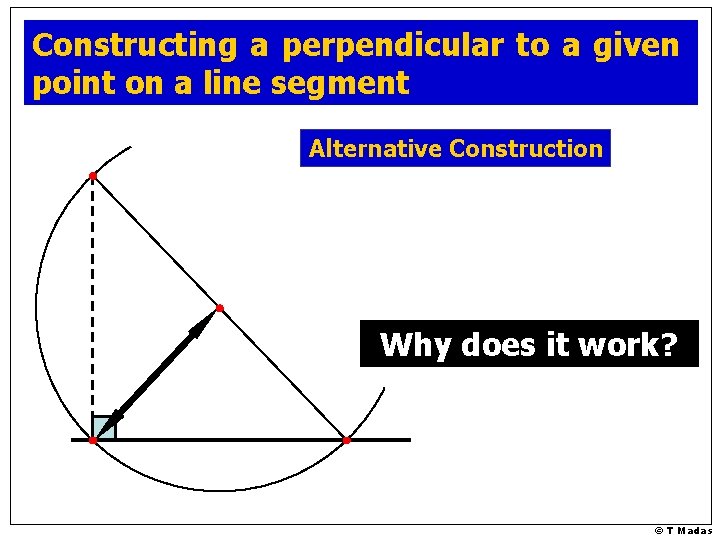
Constructing a perpendicular to a given point on a line segment Alternative Construction Why does it work? © T Madas

Constructing a perpendicular to a given point outside a line © T Madas

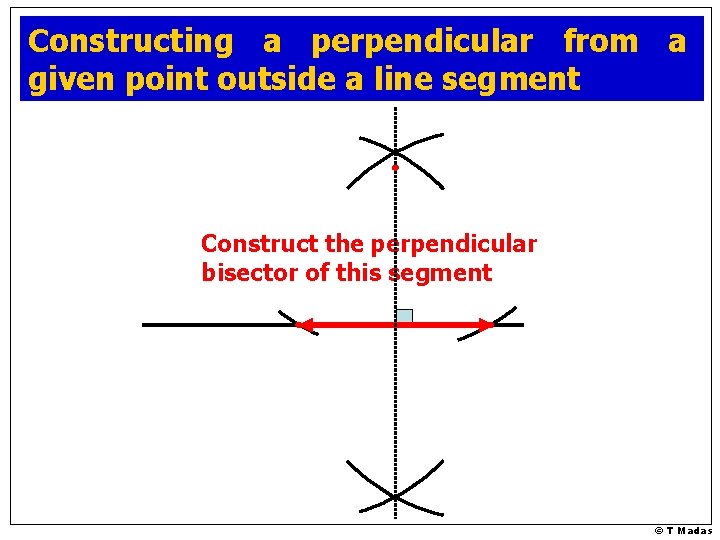
Constructing a perpendicular from a given point outside a line segment Construct the perpendicular bisector of this segment © T Madas

Constructing an identical triangle to one given © T Madas

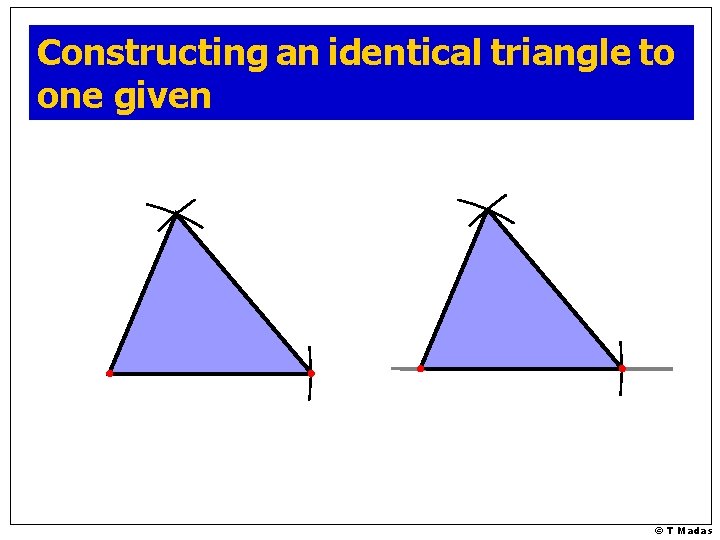
Constructing an identical angle to one given © T Madas

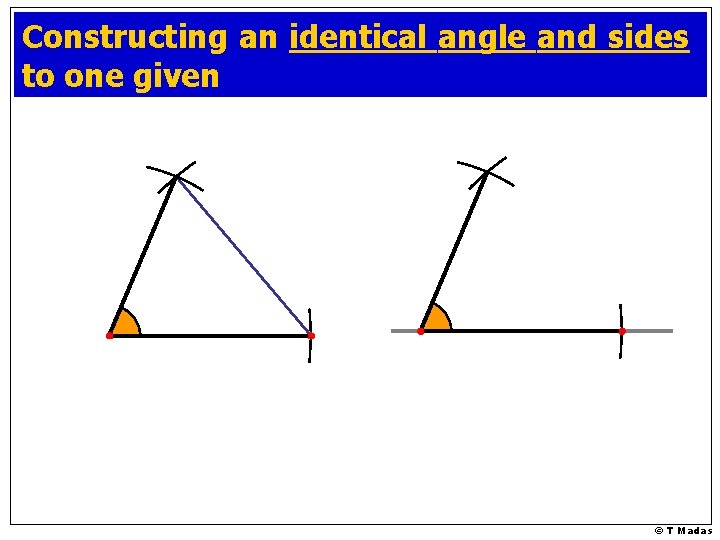
Constructing an identical angle and sides to one given © T Madas

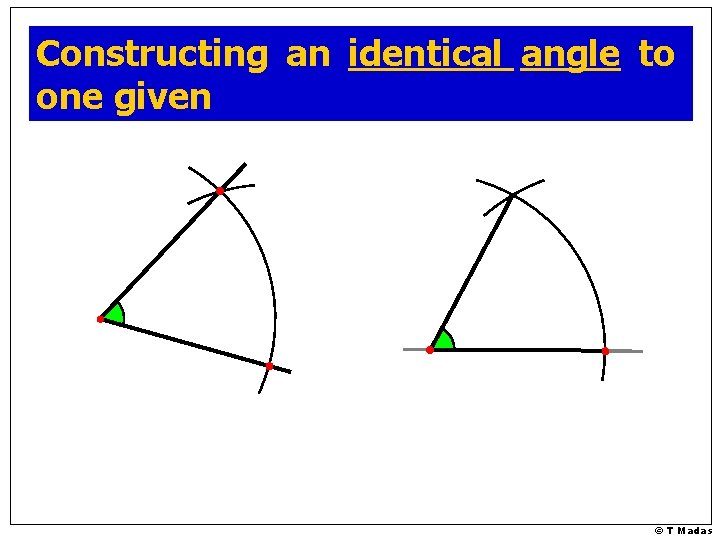
Constructing an identical angle to one given © T Madas

Constructing a parallel line to a given line, through a given point © T Madas

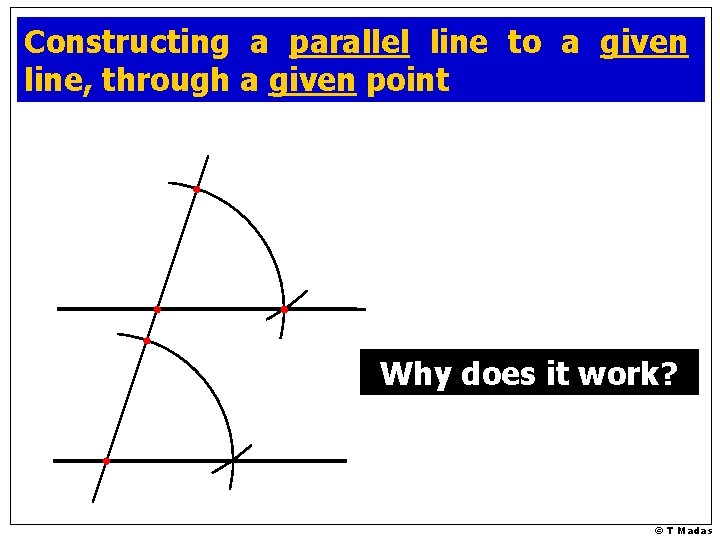
Constructing a parallel line to a given line, through a given point Why does it work? © T Madas

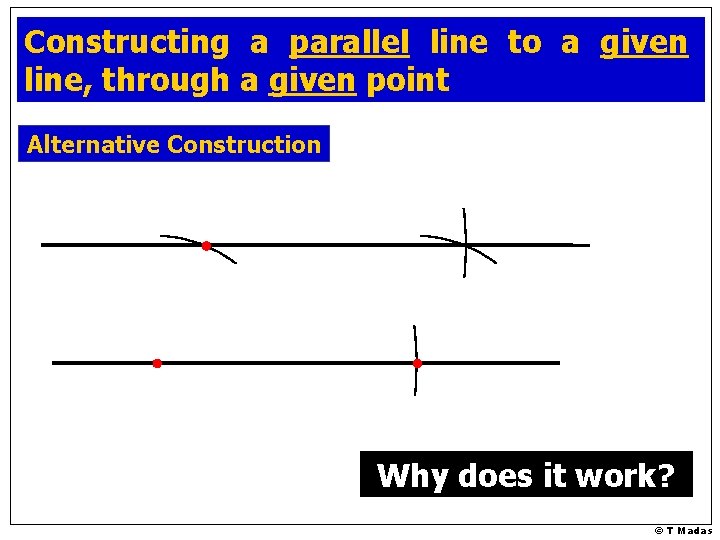
Constructing a parallel line to a given line, through a given point Alternative Construction Why does it work? © T Madas

Circumscribing a triangle © T Madas

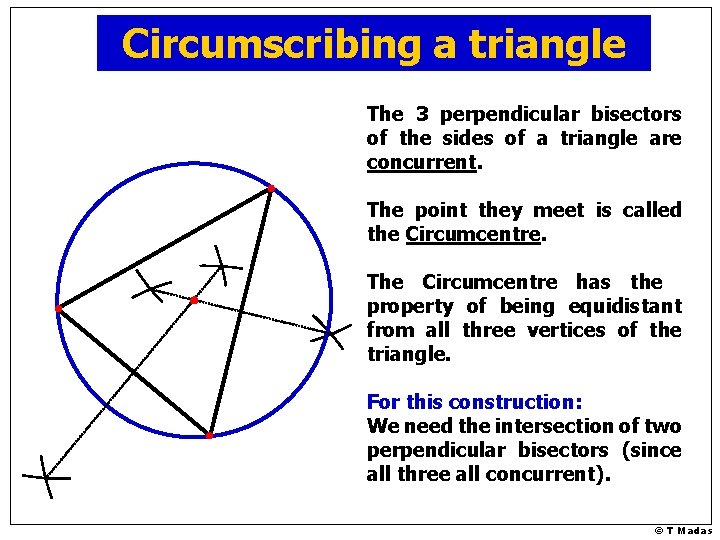
Circumscribing a triangle The 3 perpendicular bisectors of the sides of a triangle are concurrent. The point they meet is called the Circumcentre. The Circumcentre has the property of being equidistant from all three vertices of the triangle. For this construction: We need the intersection of two perpendicular bisectors (since all three all concurrent). © T Madas

Inscribing a triangle in a circle © T Madas

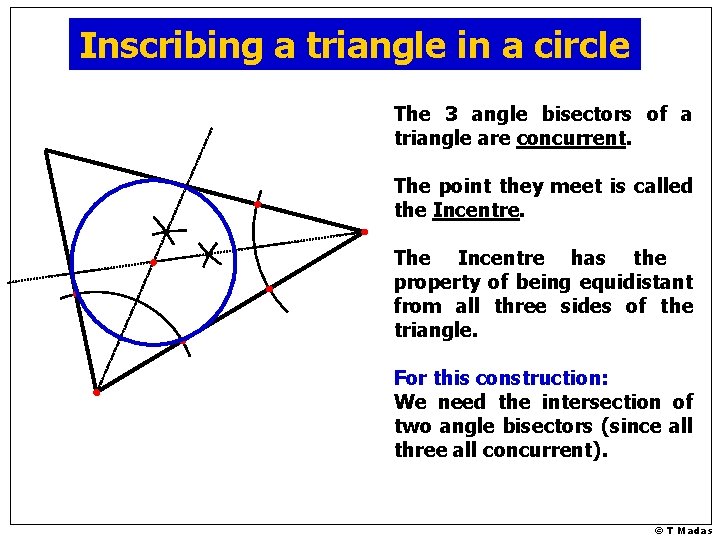
Inscribing a triangle in a circle The 3 angle bisectors of a triangle are concurrent. The point they meet is called the Incentre. The Incentre has the property of being equidistant from all three sides of the triangle. For this construction: We need the intersection of two angle bisectors (since all three all concurrent). © T Madas

Dividing a line into a given number of equal segments © T Madas

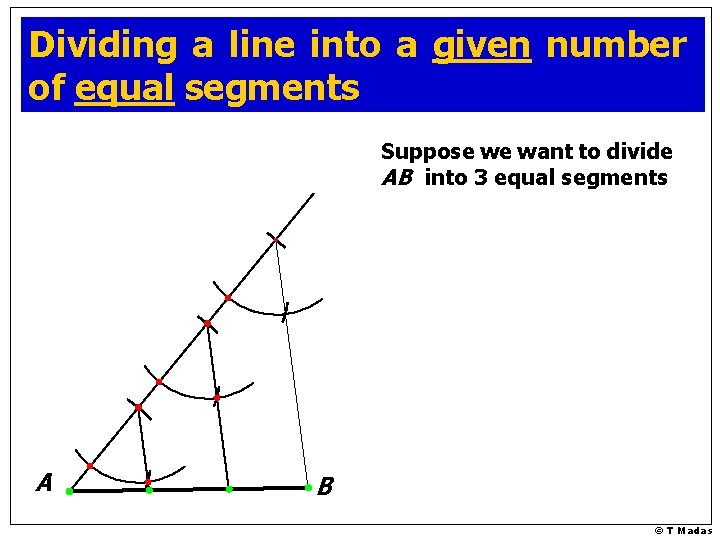
Dividing a line into a given number of equal segments Suppose we want to divide AB into 3 equal segments A B © T Madas

Construct: 1. The midpoint of a line segment 2. The perpendicular bisector of a line segment 3. The angle bisector of an acute angle 4. The angle bisector of an obtuse angle 5. An equilateral triangle 6. A triangle with sides: 3 cm, 4 cm and 6 cm 7. A 45° angle 8. A 60° angle 9. A 120° angle 10. The perpendicular to a line segment through a given point on the line segment 11. The perpendicular to a line segment through a given point outside the line segment 12. A parallel line to a line segment which passes through a point outside the line segment © T Madas

Constructing a Regular Hexagon Why does it work? © T Madas

Constructing Regular Pentagons © T Madas

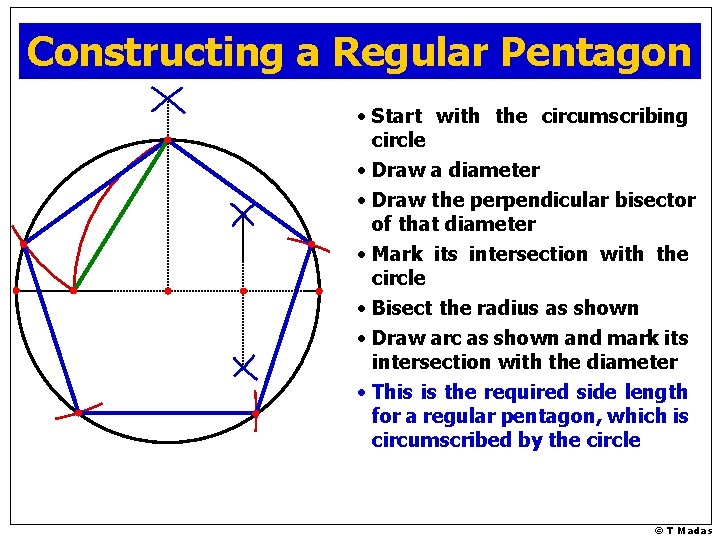
Constructing a Regular Pentagon • Start with the circumscribing circle • Draw a diameter • Draw the perpendicular bisector of that diameter • Mark its intersection with the circle • Bisect the radius as shown • Draw arc as shown and mark its intersection with the diameter • This is the required side length for a regular pentagon, which is circumscribed by the circle © T Madas

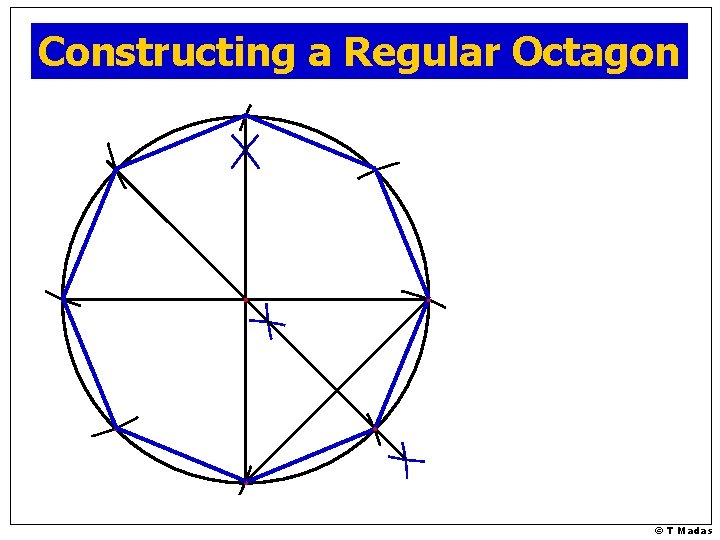
Constructing a Regular Octagon © T Madas

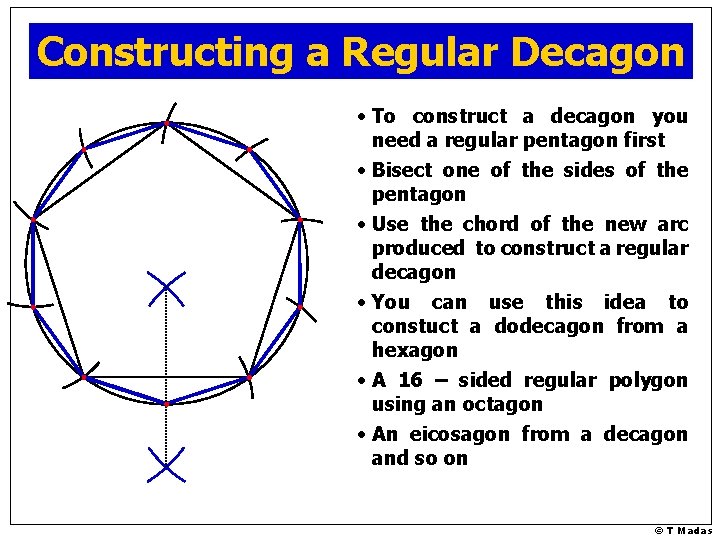
Constructing a Regular Decagon • To construct a decagon you need a regular pentagon first • Bisect one of the sides of the pentagon • Use the chord of the new arc produced to construct a regular decagon • You can use this idea to constuct a dodecagon from a hexagon • A 16 – sided regular polygon using an octagon • An eicosagon from a decagon and so on © T Madas