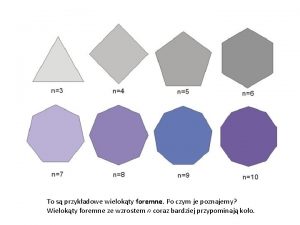
Geometria Krtki kurs geometrii paszczyzny Kty i wielokty

Geometria Krótki kurs geometrii płaszczyzny

Kąty i wielokąty

Nazwy i własności kątów powstających przez przecinające się proste

* Suma kątów przyległych wynosi 180 o

Trójkąty

Z trzech odcinków można zbudować trójkąt tylko wtedy, gdy suma dwóch krótszych odcinków jest większa od najdłuższego.

Rodzaje trójkątów

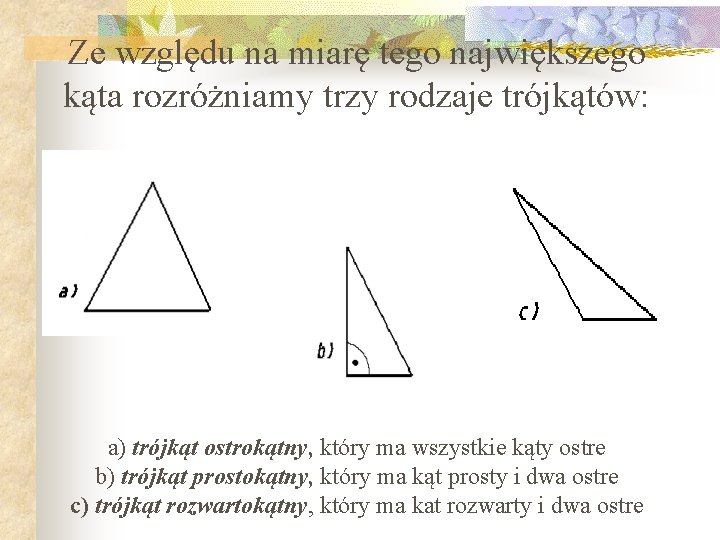
Ze względu na miarę tego największego kąta rozróżniamy trzy rodzaje trójkątów: a) trójkąt ostrokątny, który ma wszystkie kąty ostre b) trójkąt prostokątny, który ma kąt prosty i dwa ostre c) trójkąt rozwartokątny, który ma kat rozwarty i dwa ostre

Ze względu na boki wyróżniamy także trzy rodzaje trójkątów: a) trójkąt równoboczny b) trójkąt równoramienny c) trójkąt różnoboczny

W trójkącie wyróżniamy: 1. wysokość trójkąta 2. symetralna boku 3. dwusieczna kąta

Ćwiczenie 1. Czy istnieje trójkąt rozwartokątny, w którym najmniejszy kąt ma miarę 45 o ?

Symetrie i czworokąty

Figura może mieć symetrię osiową lub środkową, symetrię osiową i środkową, albo nie mieć żadnej z tych symetrii.

Rozróżniamy dwa podstawowe rodzaje symetrii: - symetria względem prostej, czyli symetria osiowa; - symetria względem punktu, czyli symetria środkowa.

Symetria w czworokątach

Kwadrat • wszystkie boki równe • przeciwległe boki równoległe • wszystkie kąty proste • przekątne są równe, dzieląc się na połowy i są prostopadłe • symetria osiowa • symetria środkowa

Prostokąt • przeciwległe boki równe i równoległe • wszystkie kąty proste • przekątne są równe i dzielą się na połowy • symetria osiowa • symetria środkowa

Romb • wszystkie boki równe • przeciwległe boki równoległe • przeciwległe kąty równe • przekątne dzielą się na połowy i są prostopadłe • symetria osiowa • symetria środkowa

Deltoid • dwie pary sąsiednich boków równych • przekątne są prostopadłe • symetria osiowa

Trapez równoramienny • podstawy równoległe • symetria osiowa

Równoległobok • przeciwległe boki równe i równoległe • przeciwległe kąty równe • przekątne dzielą się na połowy • symetria środkowa * Każdy równoległobok ma oś symetrii. Jest nim punkt przecięcia przekątnych.

Ćwiczenie 1. Czy istniej trapez, który ma dokładnie jeden kąt prosty?

Okrąg i koło

Kąty w kole

n Kąt wpisany oparty na średnicy okręgu jest prosty.

n Kąt wpisany ma dwa razy mniejszą miarę niż kąt środkowy oparty na tym samym łuku.

n Kąty wpisane oparte na tym samym łuku są równe.

Ćwiczenia 1. Oblicz kąty w podanych trójkątach

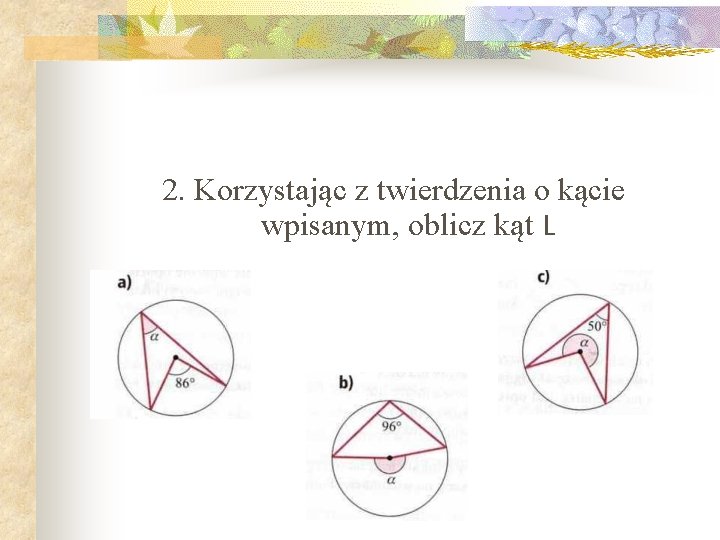
2. Korzystając z twierdzenia o kącie wpisanym, oblicz kąt L

Figury opisane czy wpisane ? ? ?

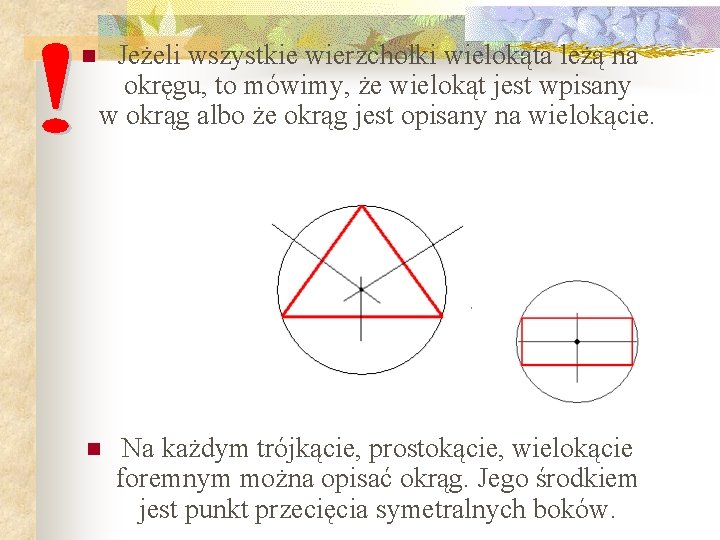
n Jeżeli wszystkie wierzchołki wielokąta leżą na okręgu, to mówimy, że wielokąt jest wpisany w okrąg albo że okrąg jest opisany na wielokącie. n Na każdym trójkącie, prostokącie, wielokącie foremnym można opisać okrąg. Jego środkiem jest punkt przecięcia symetralnych boków.

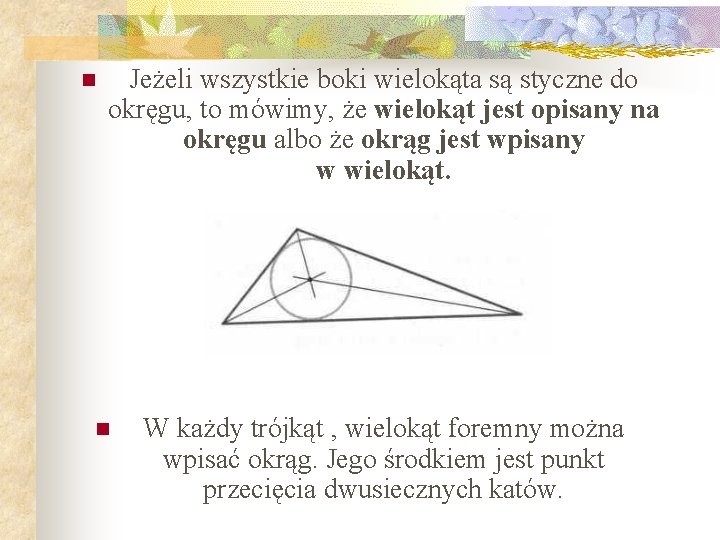
n Jeżeli wszystkie boki wielokąta są styczne do okręgu, to mówimy, że wielokąt jest opisany na okręgu albo że okrąg jest wpisany w wielokąt. n W każdy trójkąt , wielokąt foremny można wpisać okrąg. Jego środkiem jest punkt przecięcia dwusiecznych katów.

Pola, obwody i twierdzenie Pitagorasa

Pitagoras (ok. 570 -491 p. n. e) Grecki matematyk i filozof; założyciel szkoły pitagorejskiej; stworzył twierdzenie o bokach w trójkącie prostokątnym zwane twierdzeniem Pitagorasa

Twierdzenie Pitagorasa W trójkącie prostokątnym suma kwadratów przyprostokątnych jest równa kwadratowi przeciwprostokątnej a 2 + b 2 = c 2

Ćwiczenia 1. Oblicz szukane boki trójkątów.

Zastosowanie twierdzenia Pitagorasa w układzie współrzędnych

Odległość punktów o znanych współrzędnych obliczamy, korzystając z twierdzenia Pitagorasa. Na przykład odległość punktów P=(1, -2) i Q=(3, 4) wyznaczamy z trójkąta prostokątnego PRQ: [PQ]2=[PR]2+[RQ]2 [PQ]2=(3 -1)2+(4 -(-2))2 [PQ]2=4+36 [PQ]2=40/ [P Q]= 40

Przystawanie

Figury nazywamy przystającymi, gdy mają taki sam kształt i taką samą wielkość. Po wycięciu nakładają się na siebie. Aby sprawdzić, że dwa trójkąty są podobne korzystamy z przedstawionych warunków:

Cecha BBB - bok bok Trzy boki jednego trójkąta są równe odpowiednim bokom drugiego trójkąta. n

Cech BKB – bok kąt bok Dwa boki i kat zawarty między nimi w jednym trójkącie są równe odpowiednim bokom i kątowi między nimi w drugim trójkącie. n

Cecha KBK- kąt bok kąt Bok i dwa kąty leżące przy tym boku w jednym trójkącie są równe odpowiedniemu bokowi i kątom w drugim trójkącie. n

Ćwiczenia 1. Sprawdź czy te trójkąty są przystające. Z jakiej cechy skorzystałeś?

Dziękujemy za obejrzenie prezentacji przygotowanej przez uczennice klasy III e Publicznego Gimnazjum w Osięcinach : Katarzynę Sławińską i Monikę Dankiewicz