Geometria Computacional Prof Walter Mascarenhas Segundo semestre de

Geometria Computacional Prof. Walter Mascarenhas Segundo semestre de 2004 Aula 6

Triangulação em O(n logn) 1 - Ordene os pontos pela coordenada y O(n logn) 2 - Decomponha o polígono em trapézios usando uma scanline O(n logn) 3 - Usando os trapézios, quebre o polígono em partes monótonas através da eliminação das cúspides internas O(n) 4 - Triangule as partes monótonas O(n)

Vértices reflexos e cúspides internas Um vértice v de um polígono P é reflexo seu ângulo interno é estritamente maior que pi. Um vértice reflexo r é uma cúspide interna de P com relação à reta r se seus dois vizinhos estão contidos no mesmo semi-plano fechado definido pela paralela a r que passa por v.

Partição em trapézios Um polígono particionado em trapézios (triângulos são trapézios degenerados. ) Note que o lado inferior de cada trapézio contém exatamente um vértice e o superior também

Método da scanline

Poligonais estritamente monótonas Uma poligonal P é estritamente monótona com respeito à uma reta r se toda perpendicular à r corta P em no máximo um ponto

Poligonais monótonas Uma poligonal P é monótona com respeito à uma reta r se toda perpendicular à r corta P em no máximo uma componente conexa

Observação

Polígonos monótonos Uma polígono é (estritamente) monótono com respeito à uma reta r se puder ser particionado em duas poligonais que são (estritamente) monótonas com respeito a r

Conseqüência da observação passada

Critério de não monotonicidade Lema: Um polígono P não monótono com relação a uma reta r contém pelo menos uma cúspide interna com relação a r. . A recíproca deste lema e versões mais fortes são falsas:

Porque o lema é correto

Porque é chato provar o lema

Prova: simplifique o polígono 1 - Polígonos com menos vértices são mais simples 2 - Polígonos com “máximos locais” mais para baixo são mais simples 3 - Polígonos com “mínimos locais” mais para cima são mais simples

Se não der para simplificar então há cúspides

Prova 1 - Remova todos os máximos locais com pelo menos um vizinho acima da reta “crítica” 2 - Remova todos os mínimos locais com pelo menos um vizinho abaixo da reta crítica. . 3 - Os vértices do polígono resultante não podem ter os dois vizinhos em lados opostos da reta crítica! 4 - O polígono resultante é um ``zig zag’’ 5 - Dentre três vértices consecutivos em um zig-zag há uma cúspide

Prova

Prova

De trapézios para partes monótonas: Basta remover as cúspides internas conectando-as da seguinte maneira: 1 - Uma cúspide interna que está no lado inferior de um trapézio é ligada ao vértice do polígono que está no lado superior do mesmo trapézio por uma diagonal 2 - Uma cúspide interna que está no lado superior de um trapézio é ligada ao vértice do polígono que está no lado inferior do mesmo trapézio por uma diagonal

De trapezóides para partes monótonas:

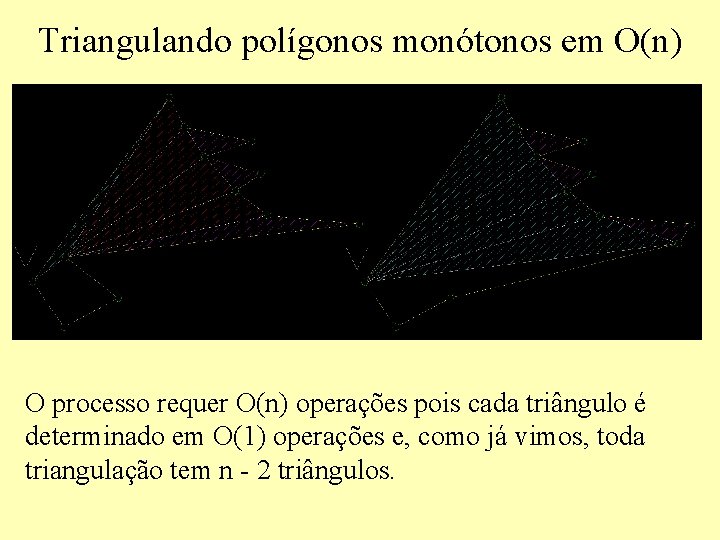
Triangulando polígonos monótonos em O(n)

Triangulando polígonos monótonos em O(n) A partir do topo, escolha o lado no qual o segundo vértice (v) está mais baixo (esquerda neste caso). Percorra os vértices no lado oposto a v, removendo os vértices convexos, como indicado na figura

Triangulando polígonos monótonos em O(n) A remoção de vértices convexos é recursiva, até que restem apenas vértices reversos.

Triangulando polígonos monótonos em O(n) Após a remoção dos vértices convexos, os vértices restantes podem ser ligados a v, definindo triângulos. Após a remoção destes triângulos, o vértice do topo é atualizado.

Triangulando polígonos monótonos em O(n) O processo requer O(n) operações pois cada triângulo é determinado em O(1) operações e, como já vimos, toda triangulação tem n - 2 triângulos.

Contando o número de operações Para contar as operações montaremos uma planilha com duas colunas: uma listará os vértices pendentes e a outra conterá os vértices “externos” em triângulos removidos. A cada passo atualizaremos o “cursor” (em vermelho).

Contando o número de operações No primeiro passo verificamos qual dos vizinhos do vértice 1 está mais abaixo, inserimos o vértice 1 na lista de pendências e movemos o cursor para o vizinho mais baixo.

Como o vértice anterior ao 2 é o 1 e o vértice 3 está acima do 11, coloco o 2 na coluna de pendências e movo o cursor para o 3.

O vértice anterior ao 3, o 2, é reverso: coloco o 3 na coluna de pendências e movo o cursor para o 4.

O vértice 3 é convexo: formo o triângulo 2 -3 -4, coloco 3 na coluna “Triang” e mantenho o cursor em 4.

O vértice anterior ao 4, o 2, é reverso: coloco o 4 na coluna de pendências e movo o cursor para 5.

O vértice anterior ao 5, o 4, é reverso: coloco o 5 na coluna de pendências e movo o cursor para 6.

O vértice anterior ao 6, o 4, é reverso: insiro o 6 na coluna de pendências e movo o cursor para o 7.

O vértice anterior ao 7, o 6, é reverso: insiro o 7 na coluna de pendências e movo o cursor para o 8.

O vértice anterior ao 8, o 7, é reverso: insiro o 8 na coluna de pendências e movo o cursor para o 9.

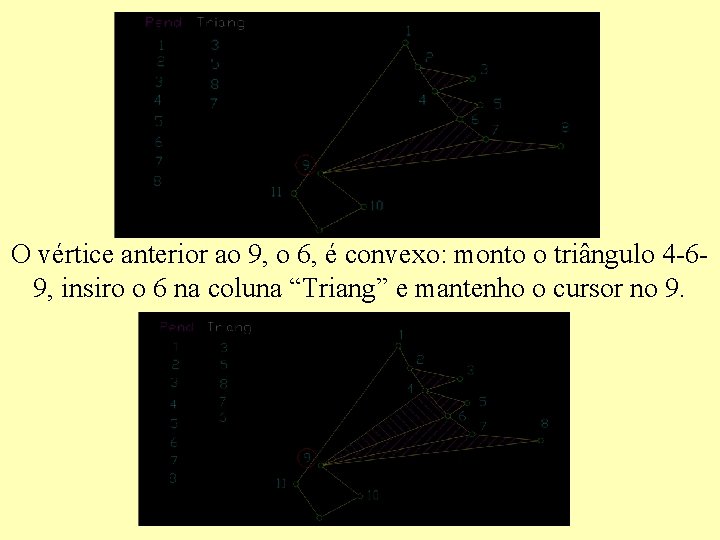
O vértice anterior ao 9, o 8, é convexo: monto o triângulo 7 -89, insiro o 8 na coluna “Triang” e mantenho o cursor no 9.

O vértice anterior ao 9, o 7, é convexo: monto o triângulo 6 -79, insiro o 7 na coluna “Triang” e mantenho o cursor no 9.

O vértice anterior ao 9, o 6, é convexo: monto o triângulo 4 -69, insiro o 6 na coluna “Triang” e mantenho o cursor no 9.

O vértice anterior ao 9, o 4, é convexo: monto o triângulo 2 -49, insiro o 4 na coluna “Triang” e mantenho o cursor no 9.

O vértice anterior ao 9, o 2, é convexo: monto o triângulo 1 -29, insiro o 2 na coluna “Triang” e mantenho o cursor no 9.

O vértice anterior ao 9 é o 1 e o vértice 10 está abaixo do 11: monto o triângulo 9 -1 -11, insiro o 1 na coluna “Triang” e repito o processo para os vértices abaixo do 9 (note que estamos numa situação similar à que estávamos ao analisar o vértice 1).

Estimativa final do número de operações 1 - A cada passo inserimos alguém ou na coluna de pendências ou na de triângulos. Cada passo requer O(1) operações. Logo o número de operações é da ordem do número de elementos na duas colunas. 2 - Cada vértice só é inserido uma vez na coluna de triângulos, pois no momento da inserção ele é removido do polígono 3 - Cada vértice só é inserido uma vez na coluna de pendências, no momento em que o cursor se move dele para um vértice inferior. Conclusão: o número de operações é da ordem é O(2 n) = O(n).