Geometria analitica Punti rette circonferenze e altre figure

Geometria analitica • Punti, rette, circonferenze e altre figure geometriche sono descritti mediante equazioni • I problemi geometrici sono risolti con metodi algebrici • Questa trattazione algebrica di problemi geometrici si ottiene mediante l’introduzione del piano cartesiano

Il piano cartesiano E’ formato da: • due rette orientate tra loro perpendicolari; • un segmento scelto come unità di misura; 1 asse delle ordinate y asse delle ascisse ……. . -4 -3 -2 -1 1 2 3 4 ………. x

Coordinate cartesiane di un punto - consideriamo un punto A del piano - siano i punti A 1 e A 2 le proiezioni ortogonali di A sugli assi cartesiani y 6 x. A = 3 = ascissa di A y. A = 6 = ordinata di A A 2 A ( 3; 6 ) Si dice ascissa di A la misura del segmento orientato OA 1 O A 1 3 Si dice ordinata di A la misura del segmento orientato OA 2 x ogni punto del piano determina una coppia di numeri reali

Coordinate cartesiane di un punto Consideriamo una coppia di numeri reali y I due numeri sono le coordinate di un unico punto del piano Ogni coppia di numeri reali determina un punto del piano 5 x -4 B (-4; 5 )

Coordinate cartesiane Esiste una corrispondenza biunivoca tra punti del piano e coppie di numeri reali GEOMETRIA ALGEBRA

Coordinatecartesiane Coordinate II quadrante (-; +) y I quadrante (+; +) ( -6; 5 ) ( 3; 3 ) x (- 5/2; - 4 ) III quadrante (-; -) (√ 20; - 3 ) IV quadrante (+ ; - )

Distanza tra due punti aventi la stessa ordinata y Es. 1 B( 2 ; 4 ) AB = 5 B(-4; -1 ) AB = 6 A( 7 ; 4 ) = 7 - 2 = x. A- x. B = |2 – 7| = |x. B- x. A| x A( 2; -1 ) = 2 - (- 4) = x. A- x. B = |-4 - 2| = |x. B- x. A| Es. 2

Distanza tra due punti aventi la stessa ordinata In generale, dati due punti y con la stessa ordinata A ( x. A ; y ) B ( x. B ; y ) AB = | x. B – x. A| la loro distanza è data da: y A B x x. A x. B

Distanza tra due punti aventi la stessa ascissa y Analogamente, dati due punti con la stessa ascissa A ( x; y. A ) la loro distanza è data da: B B ( x; y. B ) AB = | y. B – y. A| y. B A y. A x x

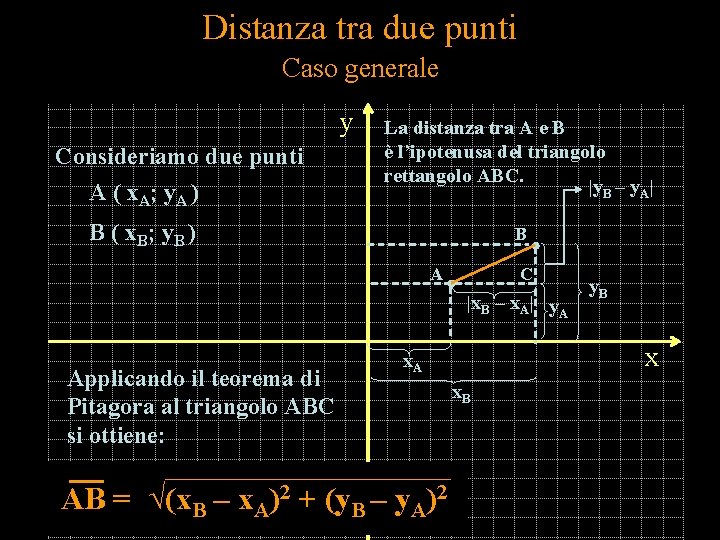
Distanza tra due punti Caso generale y A ( x A ; y. A ) La distanza tra A e B è l’ipotenusa del triangolo rettangolo ABC. |y. B – y. A| B ( x B ; y. B ) B Consideriamo due punti A C |x. B – x. A| y. A Applicando il teorema di Pitagora al triangolo ABC si ottiene: x x. A AB = √(x. B – x. A)2 + (y. B – y. A)2 y. B x. B

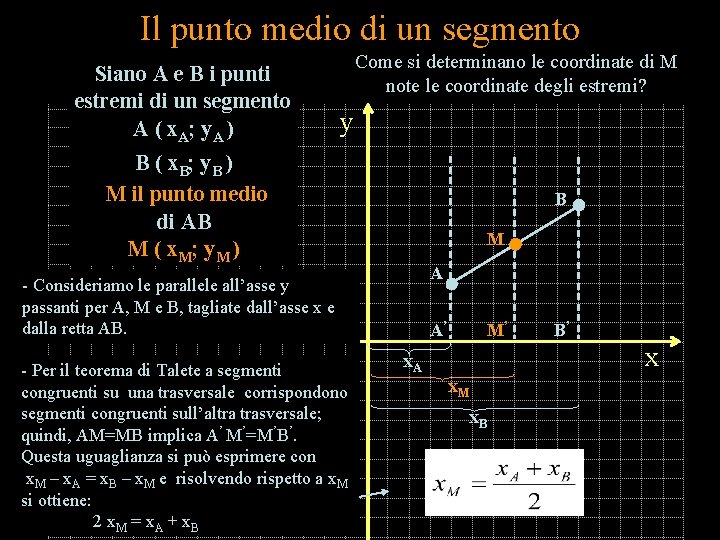
Il punto medio di un segmento Siano A e B i punti estremi di un segmento A ( x A ; y. A ) Come si determinano le coordinate di M note le coordinate degli estremi? y B ( x B ; y. B ) M il punto medio di AB M ( x M ; y. M ) B M A - Consideriamo le parallele all’asse y passanti per A, M e B, tagliate dall’asse x e dalla retta AB. - Per il teorema di Talete a segmenti congruenti su una trasversale corrispondono segmenti congruenti sull’altra trasversale; quindi, AM=MB implica A’ M’=M’B’. Questa uguaglianza si può esprimere con x. M – x. A = x. B – x. M e risolvendo rispetto a x. M si ottiene: 2 x. M = x. A + x. B A’ x. A M’ B’ x x. M x. B

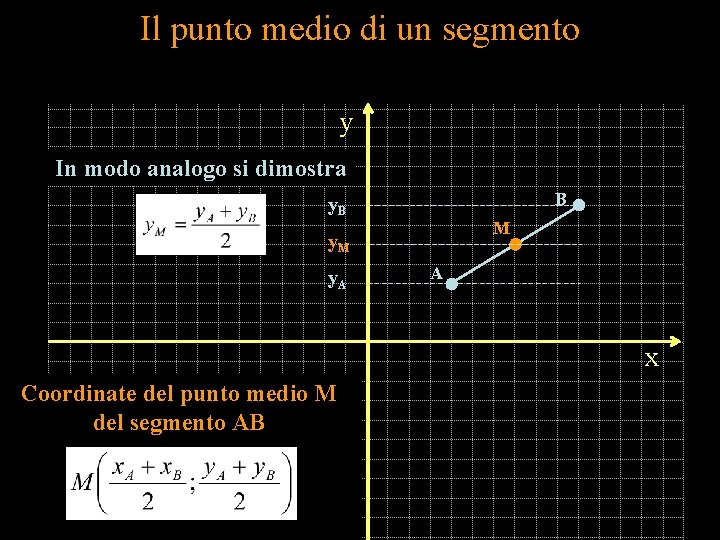
Il punto medio di un segmento y In modo analogo si dimostra B y. B M y. A A x Coordinate del punto medio M del segmento AB

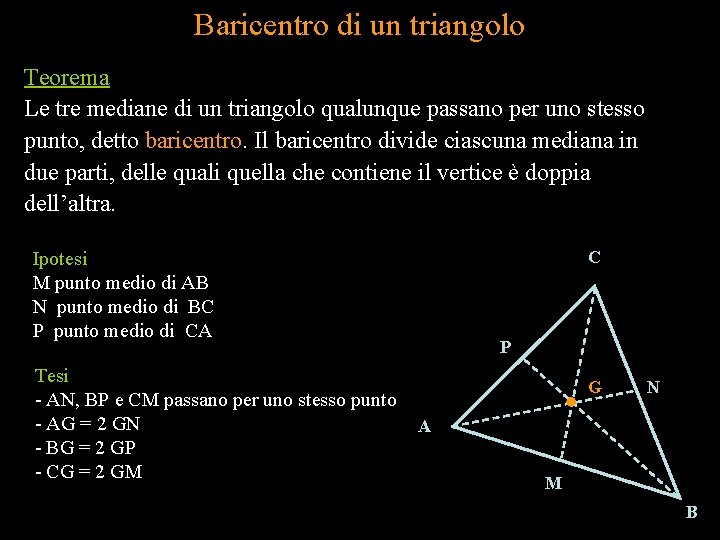
Baricentro di un triangolo Teorema Le tre mediane di un triangolo qualunque passano per uno stesso punto, detto baricentro. Il baricentro divide ciascuna mediana in due parti, delle quali quella che contiene il vertice è doppia dell’altra. C Ipotesi M punto medio di AB N punto medio di BC P punto medio di CA Tesi - AN, BP e CM passano per uno stesso punto - AG = 2 GN - BG = 2 GP - CG = 2 GM P G N A M B

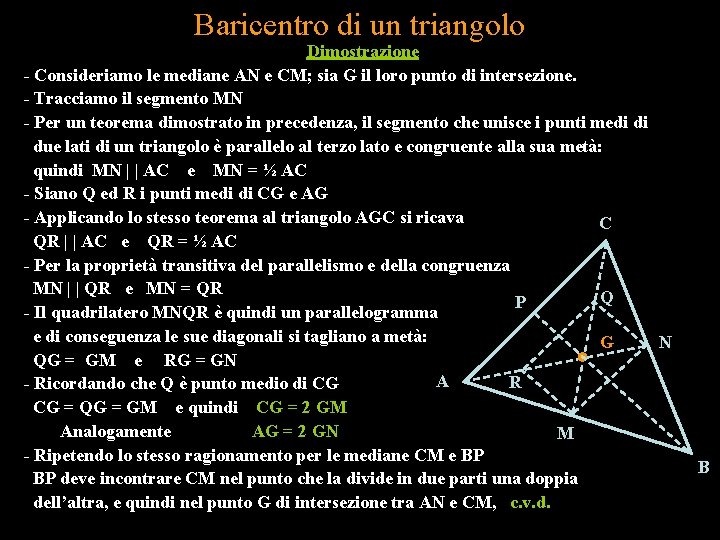
Baricentro di un triangolo Dimostrazione - Consideriamo le mediane AN e CM; sia G il loro punto di intersezione. - Tracciamo il segmento MN - Per un teorema dimostrato in precedenza, il segmento che unisce i punti medi di due lati di un triangolo è parallelo al terzo lato e congruente alla sua metà: quindi MN | | AC e MN = ½ AC - Siano Q ed R i punti medi di CG e AG - Applicando lo stesso teorema al triangolo AGC si ricava C QR | | AC e QR = ½ AC - Per la proprietà transitiva del parallelismo e della congruenza MN | | QR e MN = QR Q P - Il quadrilatero MNQR è quindi un parallelogramma e di conseguenza le sue diagonali si tagliano a metà: G N QG = GM e RG = GN A R - Ricordando che Q è punto medio di CG CG = QG = GM e quindi CG = 2 GM Analogamente AG = 2 GN M - Ripetendo lo stesso ragionamento per le mediane CM e BP BP deve incontrare CM nel punto che la divide in due parti una doppia dell’altra, e quindi nel punto G di intersezione tra AN e CM, c. v. d. B

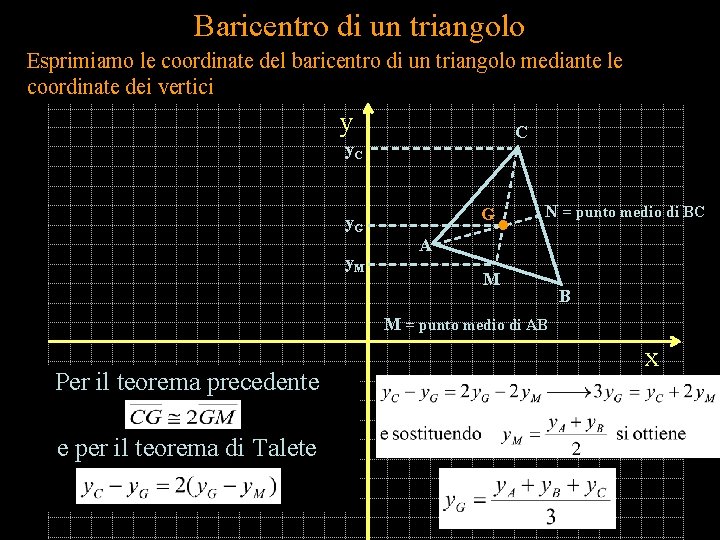
Baricentro di un triangolo Esprimiamo le coordinate del baricentro di un triangolo mediante le coordinate dei vertici y C y. C G y. M N = punto medio di BC A M B M = punto medio di AB Per il teorema precedente e per il teorema di Talete x

Baricentro di un triangolo y C In modo analogo si dimostra G N = punto medio di BC A M B M = punto medio di AB Coordinate del baricentro G del triangolo ABC x