GEOMETRI TRANSFORMASI SRI REJEKI FKIP MATEMATIKA UMS MATERI

GEOMETRI TRANSFORMASI SRI REJEKI FKIP MATEMATIKA UMS

MATERI (1) Pendahuluan Transformasi Geseran Setengah Putaran ◦ Penggolongan Geometri ◦ Geometri Euclides ◦ ◦ ◦ Fungsi dan Jenis-jenis Fungsi Transformasi Sebagai Fungsi Sifat Transformasi Grup Transformasi Pengertian Geseran Menemukan Rumus Geseran Sifat-sifat Geseran Hasil Kali Geseran Pengertian Setengah putaran Menemukan Rumus Setengah putaran Sifat-sifat Setengah putaran Hasil Kali Setengah putaran

MATERI (2) Transformasi Pencerminan Transformasi Putaran Hasil Kali Isometri Group dan Similaritas ◦ ◦ ◦ ◦ Pengertian Pencerminan Menemukan Rumus Pencerminan Sifat-sifat Pencerminan Hasil Kali Pencerminan Pengertian Putaran Menemukan Rumus Putaran Sifat-sifat Putaran Hasil Kali Putaran

REFERENSI B. Susanta Geometri Transformasi, UGM Gatut Iswahyudi Geometri Transformasi, UNS I. M Yaglom Geometric Transformations I, Yale University

PENILAIAN

KONTRAK PERKULIAHAN 1. 2. 3. 4. 5. Presensi minimal 75% … …

LAMBANG-LAMBANG KHUSUS (1) A, B, … : titik-titik g, h, … : garis-garis titik (g, h) : titik potong garis g dan h garis (A, B)= : garis melalui A dan B : sinar garis AB dengan pangkal A : ruas garis AB AB : panjang ruas garis

LAMBANG-LAMBANG KHUSUS (2) : ruas garis berarah dari A ke B : vektor dengan pangkal A ujung B A-B-C : B terletak diantara A dan C : sudut ABC : besar sudut ABC (dalam derajat) : kongruen : sebangun (similar)

PENGGOLONGAN GEOMETRI (1) Berdasar ruang lingkup 1. Geometri bidang (dimensi 2) 2. Geometri ruang (dimensi 3) 3. Geometri dimensi n 4. Geometri bola 5. dsb

PENGGOLONGAN GEOMETRI (2) Berdasar bahasa 1. Geometri murni (dengan geometri/gambar) 2. Geometri analitik (dengan bahasa aljabar) 3. Geometri differensial (dengan bahasa derivatif) 4. dsb

PENGGOLONGAN GEOMETRI (3) Berdasar sistem aksioma 1. Geometri euclides 2. Geometri non euclides 3. Geometri proyektif 4. dsb

PENGGOLONGAN GEOMETRI (4) Berdasar transformasi Berdasar metode pendekatannya dst.

CONTOH 1. 2. Dalam bidang diketahui lingkaran pusat A(0, 0) dengan jari-jari 5 Diketahui persamaan: x+2 y=4 z-y =4

TRANSFORMASI

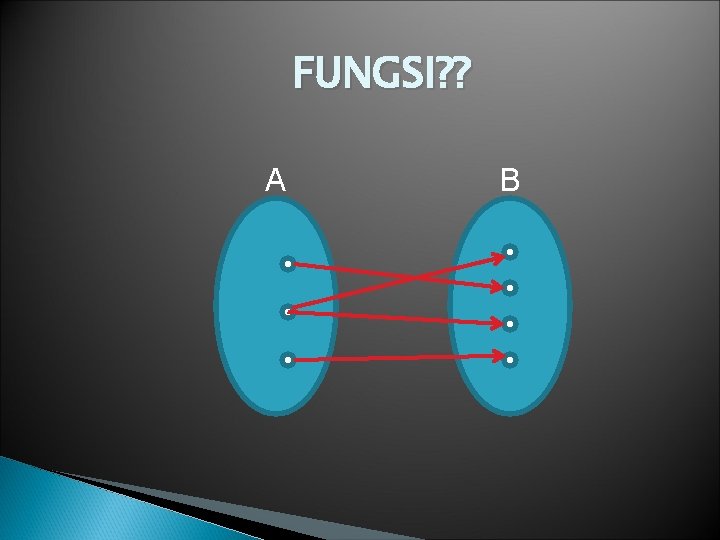
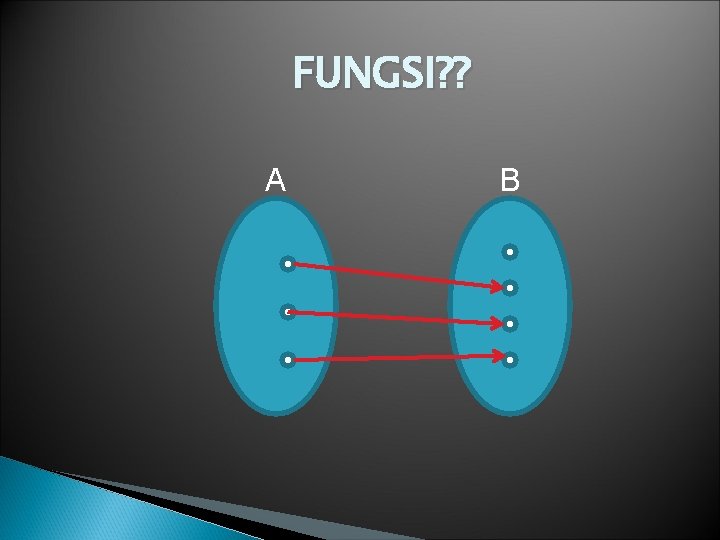
FUNGSI? ? A B

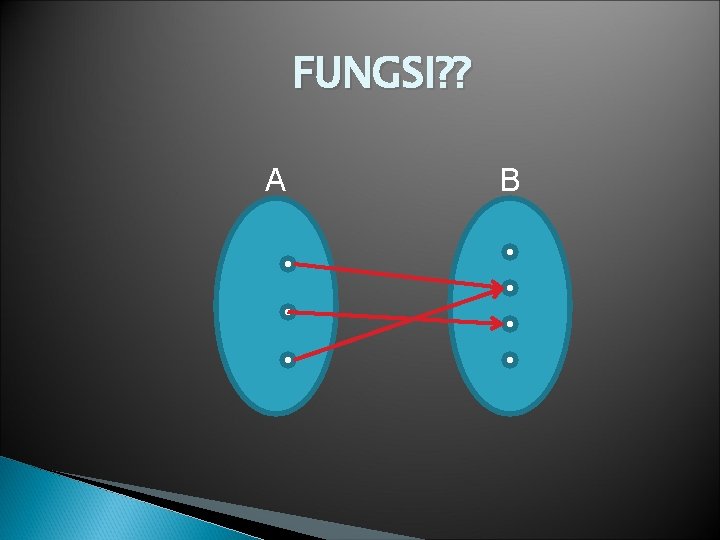
FUNGSI? ? A B

FUNGSI? ? A B

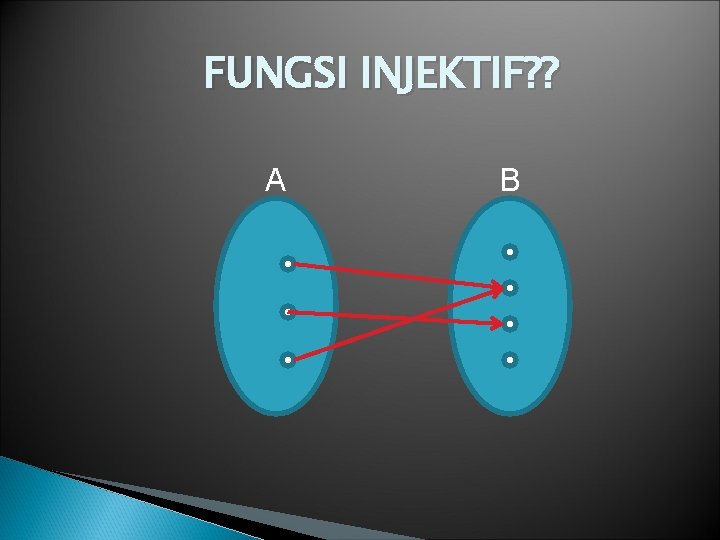
FUNGSI INJEKTIF? ? A B

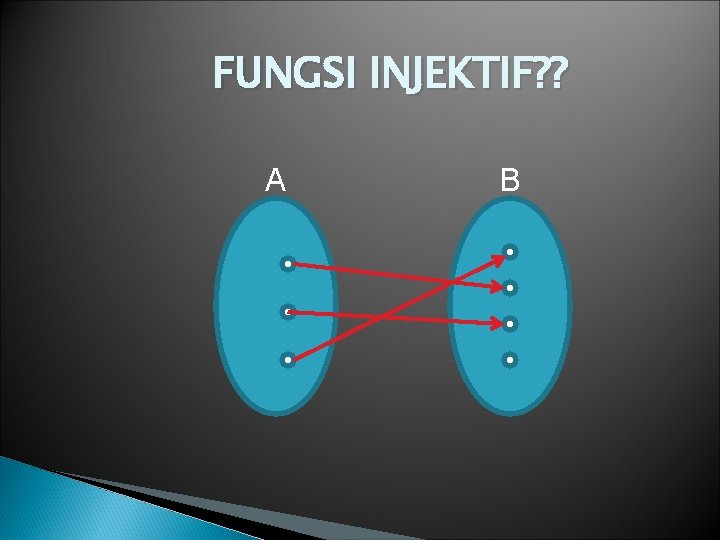
FUNGSI INJEKTIF? ? A B

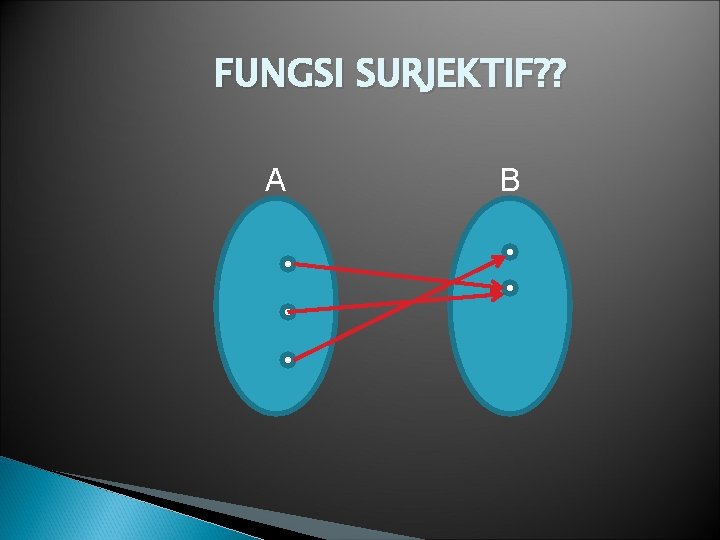
FUNGSI SURJEKTIF? ? A B

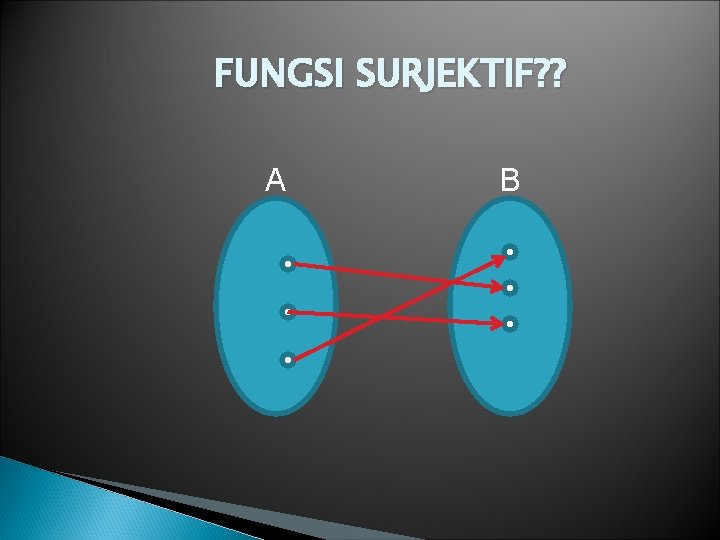
FUNGSI SURJEKTIF? ? A B

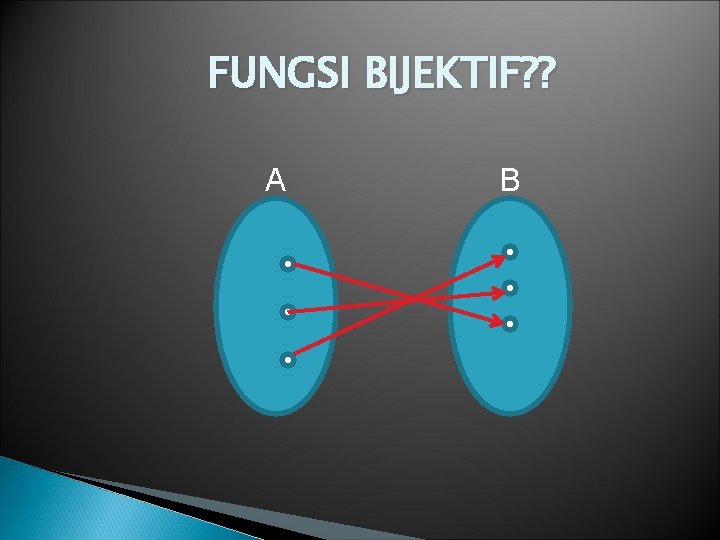
FUNGSI BIJEKTIF? ? A B

PENGERTIAN TRANSFORMASI

SIFAT-SIFAT TRANSFORMASI Unsur tetap Kolineasi Identitas Isometri Involusi

UNSUR TETAP KOLINEASI

IDENTITAS ISOMETRI

INVOLUSI

MENYELIDIKI SIFAT-SIFAT TRANSFORMASI ISOMETRI? KOLINEASI? INVOLUSI?

contoh

TEOREMA-TEOREMA Isometri adalah kolineasi atau bila U isometri dan g garis maka U(g) = g’ Isometri mempertahankan kesejajaran Isometri mempertahankan besar sudut

HASIL KALI DUA TRANSFORMASI

TEOREMA

CONTOH

GESERAN

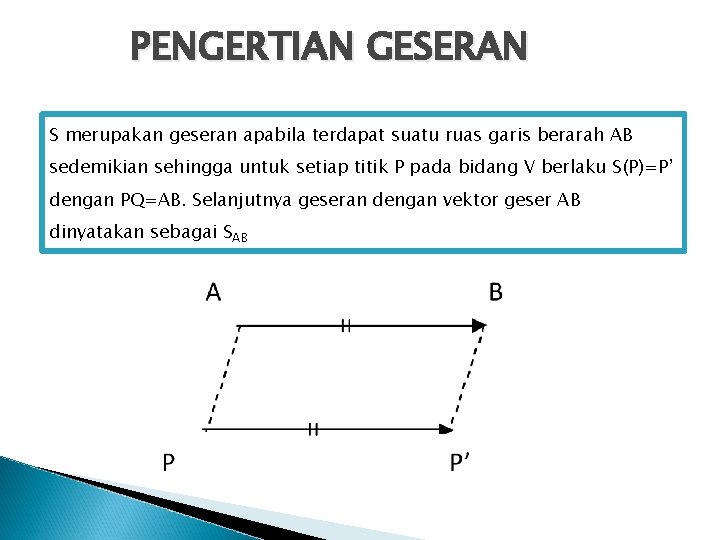
PENGERTIAN GESERAN S merupakan geseran apabila terdapat suatu ruas garis berarah AB sedemikian sehingga untuk setiap titik P pada bidang V berlaku S(P)=P’ dengan PQ=AB. Selanjutnya geseran dengan vektor geser AB dinyatakan sebagai SAB

TEOREMA-TEOREMA GESERAN

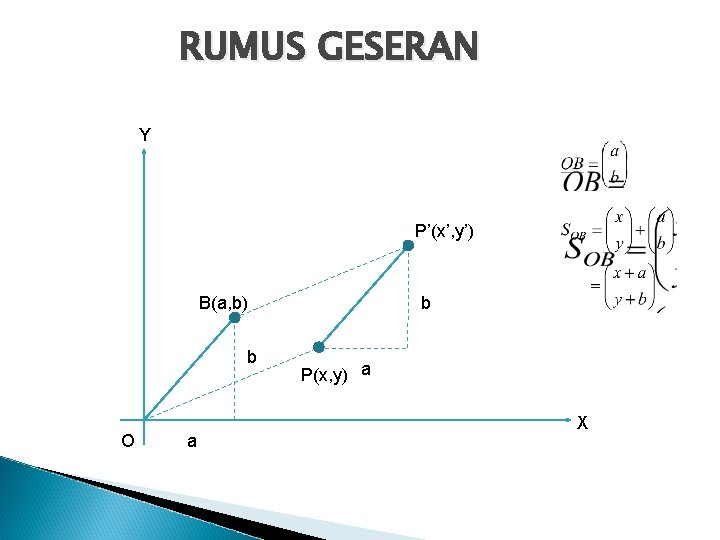
RUMUS GESERAN Y P’(x’, y’) B(a, b) b O a b P(x, y) a X

Catatan : Q(c, d) P(a, b)

soal Diketahui titik-titik A(4, -6) dan B(3, 1) 1) 2) 3) 4) 5) 6) Carilah rumus SAB dan SBA? Kena Apakah SBA kolineasi? kan SBA pada garis h di mana h melalui titik A dan tegak lurus dengan garis g : 8 x 3 y+10=9. Apakah SBA involusi? Apakah SBA isometri? Apakah hasil kali SAB dan SBA?

Sifat-sifat geseran Diketahui titik-titik A(4, -6) dan B(3, 1) ◦ Apakah SBA kolineasi? ◦ Kenakan SBA pada garis h di mana h melalui titik A dan tegak lurus dengan garis g : 8 x 3 y+10=0. ◦ Apakah SBA involusi? ◦ Apakah SBA isometri? ◦ Apakah hasil kali SAB dan SBA ?

Dari soal-soal di atas buatlah kesimpulan tentang sifat-sifat geseran, ◦ Apakah geseran merupakan suatu kolineasi? ◦ Apakah geseran merupakan involusi? ◦ Apakah geseran merupakan isometri? ◦ Apakah hasil kali geseran dengan vektor geser yang berlawanan arah?

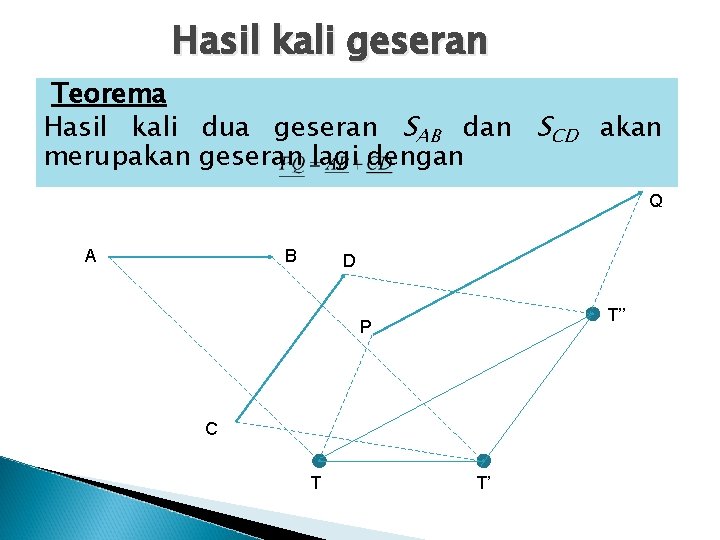
Hasil kali geseran Teorema Hasil kali dua geseran SAB dan SCD akan merupakan geseran lagi dengan Q A B D T’’ P C T T’

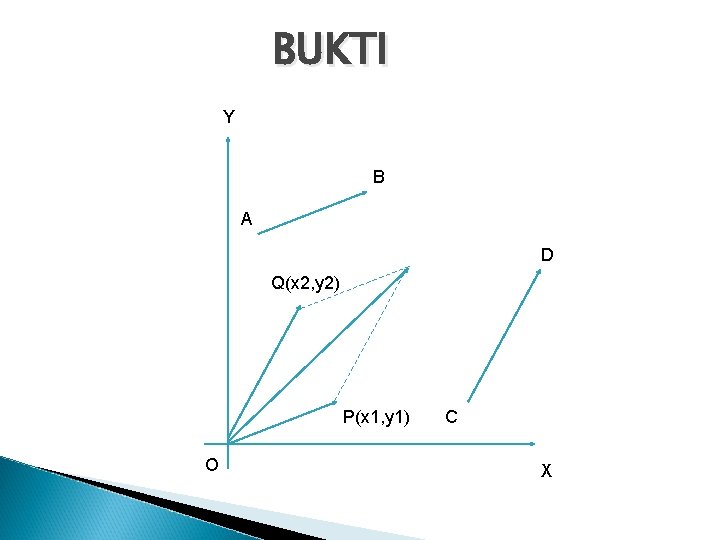
BUKTI Y B A D Q(x 2, y 2) P(x 1, y 1) O C X

Bukti analitik? ? ?

SETENGAH PUTARAN (H)

Definisi A’ Setengah putaran terhadap titik P (dengan pusat P) dilambangkan dengan Hp, adalah pemetaan yang memenuhi untuk sebarang titik A P di bidang V : 1. Jika A ≠ P maka titik P titik tengah AA’ A Hp(A)=A’ 2. Jika A = P maka Hp(A)=P=A

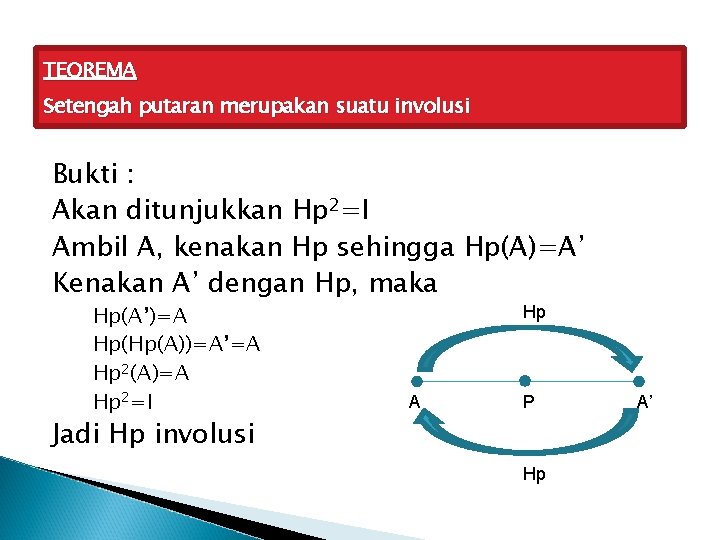
TEOREMA Setengah putaran merupakan suatu involusi Bukti : Akan ditunjukkan Hp 2=I Ambil A, kenakan Hp sehingga Hp(A)=A’ Kenakan A’ dengan Hp, maka Hp(A’)=A Hp(Hp(A))=A’=A Hp 2(A)=A Hp 2=I Hp A P Jadi Hp involusi Hp A’

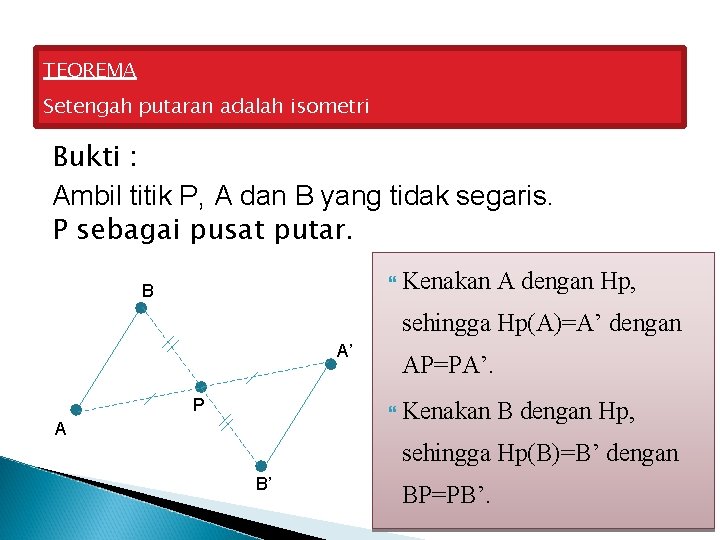
TEOREMA Setengah putaran adalah isometri Bukti : Ambil titik P, A dan B yang tidak segaris. P sebagai pusat putar. Kenakan A dengan Hp, B sehingga Hp(A)=A’ dengan A’ P AP=PA’. Kenakan B dengan Hp, A sehingga Hp(B)=B’ dengan B’ BP=PB’.

Lanjutan Perhatikan ∆APB dan ∆A’PB’ Karena AP=PA’ BP=PB’ Maka ∆APB dan ∆A’PB’ kongruen (s, sd, s) Akibat : AB=A’B’ Jadi setengah putaran adalah isometri

RUMUS SETENGAH PUTARAN Y A’(x’, y’) Ambil P(a, b) sebagai pusat putar. P(a, b) Hp memetakan A(x, y) ke A’(x’, y’). A(x, y) O X

Diperoleh hubungan bahwa : Jadi jika P(a, b) maka : Hp = (x, y)→(x’, y’) dengan

LATIHAN Diketahui A(-3, -5) dan B(-2, 3) 1. Carilah 2. Apakah 3. HB HA • HB involusi? memetakan ∆KLM ke∆K’L’M’ dengan K(3, 5), L(-5, -4) dan M(5, 6). Carilah koordinat K’, L’ dan M’ 4. Carilah Q s. d. s HA • HB(Q)=P dengan P(-4, 7)

PR 1. Diketahui A(4, 4), B(2, -5) dan P(6, 4), tentukan HA • HB(P) dan HB • HA(P). 2. Diketahui P(3, 2). Tentukan Hp((1, 3)) dan Hp-1 ((2, 4)). 3. Misalkan L={(x, y)│x 2+y 2=25}. Tentukan L’=HB • HA(L) jika A(2, 1) dan B(-3, 5). 4. Misalkan g={(x, y)│y=5 x+3} dan A(2, 3), B(-1, -2) dan C(3, 5). Tentukan SAB • Hc(g).

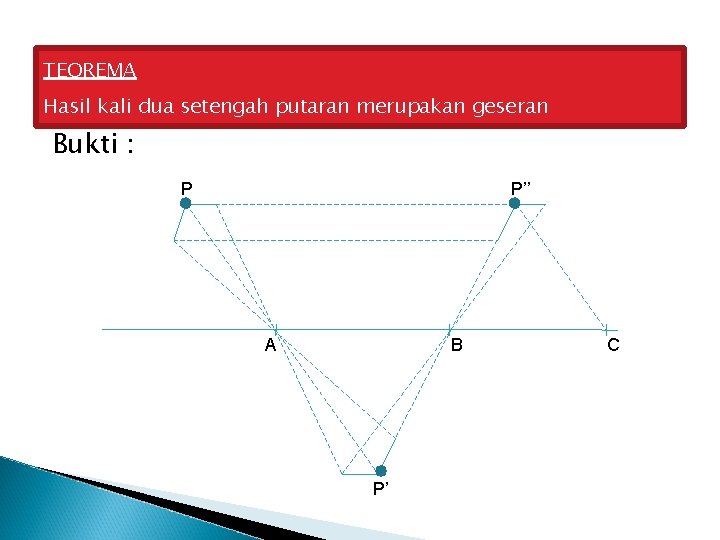
TEOREMA Hasil kali dua setengah putaran merupakan geseran Bukti : P P’’ A B P’ C

Ambil titik P, A dan B tidak segaris, kenakan P dengan HA sehingga : HA(P)=P’ berlaku PA=AP’ HB(P)=P’ berlaku P’B=BP’’ Berarti : HB(P’)=P’’ HB(HA(P))=P’’ HB • HA(P)=P’’ Karena PA=AP’ dan P’B=BP’’ Maka AB merupakan garis tengah sejajar alas PP’ dalam ∆PP’P’’ sehingga PP’’=2 AB Berarti HA • HB merupakan geseran atau HA • HB=SAC dengan AC=2 AB

Bukti secara analitik ? ? ? Hasil kali geseran dan setengah putaran ? ? ?

LATIHAN Diketahui koordinat P(-2, 8) dan R(0, 10) serta ∆A’B’C’ dengan A’(5, 1) B’(-3, -4) dan C’(1, -5). Carilah ∆ABC sehingga : HR • HP(A)=A’ HR • HP(B)=B’ HR • HP(C)=C’ Jawab : A(1, -3) B(-7, -8) C(-3, -9)

Diketahui koordinat E(-5, -1) F(1, 4) G(-2, -8) 1. Apakah hasil dari HF • HG Jawab : (6 -x, 22 -y) 2. Jika HF • HG=SED carilah koordinat D Jawab : (1, 21) 3. Kenakan HE • HF pada garis g di mana g melalui E dan tegak lurus garis yang melalui F dan G 4. Apakah hasil dari HF • HE • HG 5. Selidiki apakah HG • SEF involusi Find the answers by yourself, pasti bisa!!!

PENCERMINAN

ØPencerminan (refleksi) Transformasi pencerminan /refleksi menghasilkan bayangan yang tergantung pada acuannya.

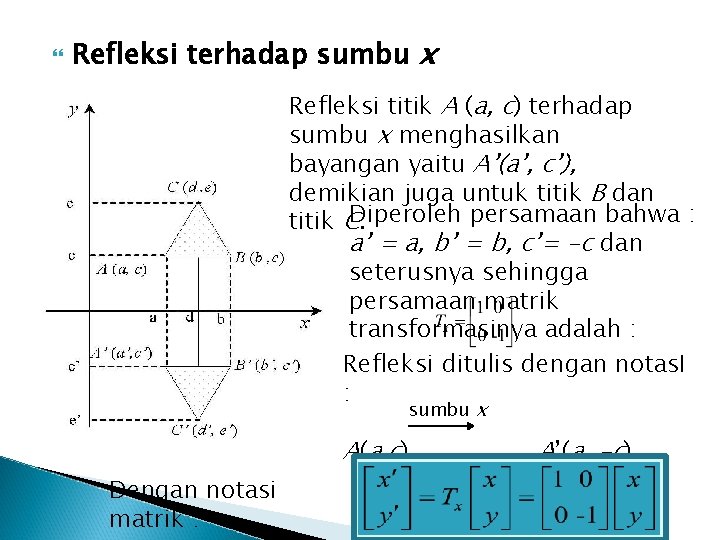
Refleksi terhadap sumbu x Refleksi titik A (a, c) terhadap sumbu x menghasilkan bayangan yaitu A’(a’, c’), demikian juga untuk titik B dan persamaan bahwa : titik CDiperoleh. a’ = a, b’ = b, c’= -c dan seterusnya sehingga persamaan matrik transformasinya adalah : Refleksi ditulis dengan notas. I : sumbu x A(a, c) Dengan notasi matrik : A’(a, -c)

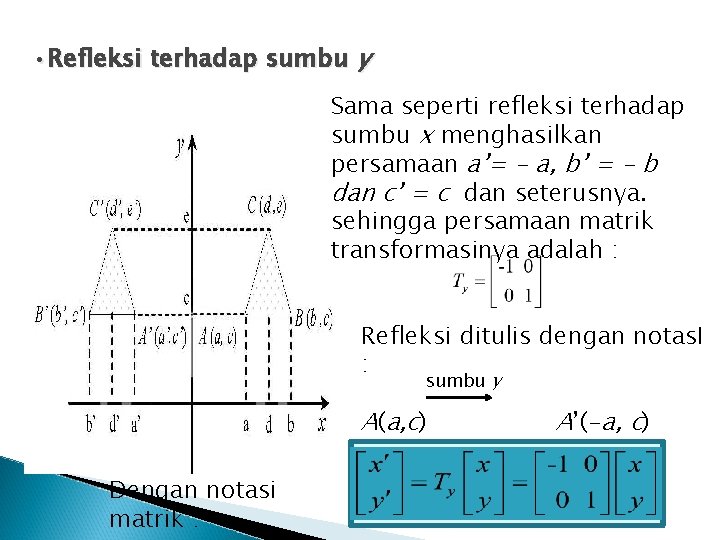
• Refleksi terhadap sumbu y Sama seperti refleksi terhadap sumbu x menghasilkan persamaan a’= - a, b’ = - b dan c’ = c dan seterusnya. sehingga persamaan matrik transformasinya adalah : Refleksi ditulis dengan notas. I : sumbu y A(a, c) Dengan notasi matrik : A’(-a, c)

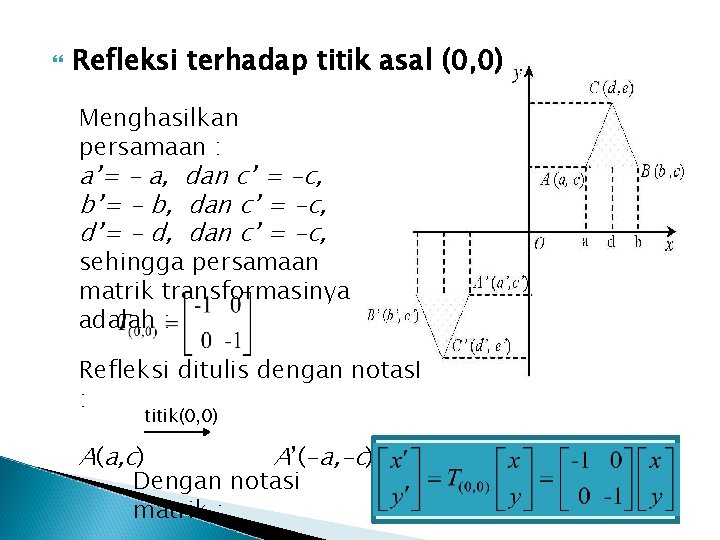
Refleksi terhadap titik asal (0, 0) Menghasilkan persamaan : a’= - a, dan c’ = -c, b’= - b, dan c’ = -c, d’= - d, dan c’ = -c, sehingga persamaan matrik transformasinya adalah : Refleksi ditulis dengan notas. I : titik(0, 0) A(a, c) A’(-a, -c) Dengan notasi matrik :

Refleksi terhadap garis y = x Menghasilkan persamaan : a’= c, dan c’ = a, b’= c, dan c’’ = b, d’= e, dan e’ = d dan seterusnya sehingga persamaan matrik transformasinya adalah : Refleksi ditulis dengan notas. I : y=x A(a, c) A’(c, a) Dengan notasi matrik :

Refleksi terhadap garis y = - x Menghasilkan persamaan : a’= -c, dan c’ = -a, b’= -c, dan c’’ = -b, d’= -e, dan e’ = -d dan seterusnya, sehingga persamaan matrik transformasinya adalah : Refleksi ditulis dengan notas. I : y =- x A(a, c) A’(-c, -a) Dengan notasi matrik :

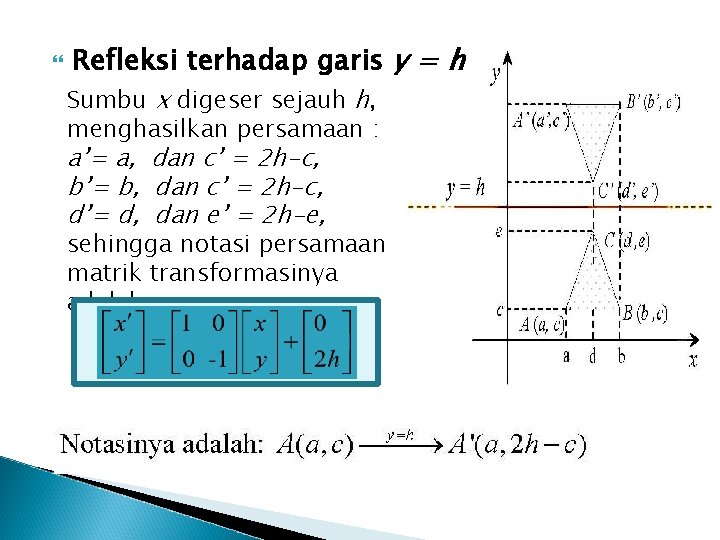
Refleksi terhadap garis y = h Sumbu x digeser sejauh h, menghasilkan persamaan : a’= a, dan c’ = 2 h-c, b’= b, dan c’ = 2 h-c, d’= d, dan e’ = 2 h-e, sehingga notasi persamaan matrik transformasinya adalah :

Bukti : Sumbu-x dipindahkan sejauh h sehingga sumbu-x yang baru adalah y = h. Maka koefisien setiap titik berubah menjadi (x’, y’) dengan : Kemudian titik tersebut direfleksikan pada sumbu-x yang baru menjadi : Tahap terakhir, menggeser sumbu-x yang baru ke sumbu-x semula dengan memakai translasi diperoleh:

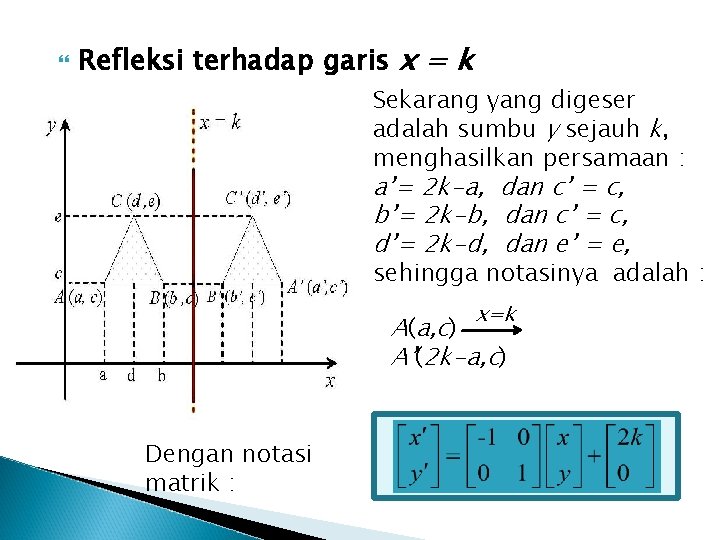
Refleksi terhadap garis x = k Sekarang yang digeser adalah sumbu y sejauh k, menghasilkan persamaan : a’= 2 k-a, dan c’ = c, b’= 2 k-b, dan c’ = c, d’= 2 k-d, dan e’ = e, sehingga notasinya adalah : x=k A(a, c) A’(2 k-a, c) Dengan notasi matrik :

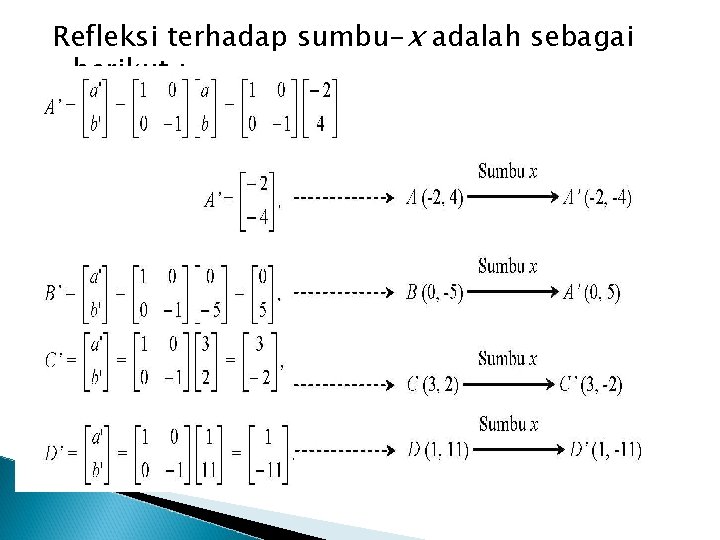
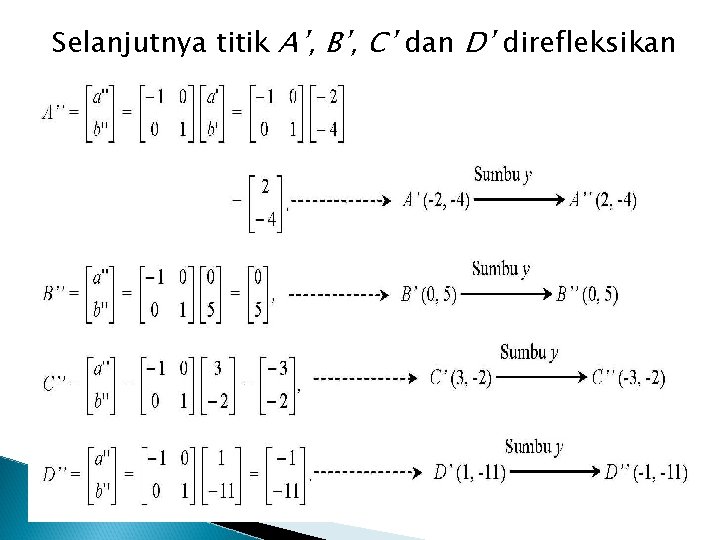
Contoh Soal : Tentukan bayangan jajaran-genjang ABCD dengan titik sudut A(-2, 4), B(0, -5) C(3, 2) dan D(1, 11) jika direfleksikan terhadap sumbu-x, kemudian dilanjutkan dengan refleksi terhadap sumbu-y. Jawab : Penyelesaian soal tersebut dilakukan dengan dua tahap yaitu mencari bayangan jajaran-genjang ABCD dari refleksi terhadap sumbu-x, kemudian bayangan yang terjadi direfleksikan terhadap

Refleksi terhadap sumbu-x adalah sebagai berikut :

Selanjutnya titik A’, B’, C’ dan D’ direfleksikan pada sb-y

Hasil akhir diperoleh jajaran-genjang A’’B’’C’’D’’ dengan titik sudut A’’(2, -4), B’’(0, 5), C’’(-3, -2) dan D’’(-1, -11). Coba pikirkan : Bagaimana cara mendapatkan matrik transformasi pada suatu sistem yang mengalami refleksi lebih dari satu kali tetapi penyelesaiannya hanya dengan mengunakan satu tahap saja ?

PUTARAN

Telah dibahas bahwa : ◦ Hasil kali 2 pencerminan dengan kedua sumbu sejajar adalah berupa geseran. ◦ Hasil kali 2 pencerminan dengan kedua sumbu yang saling tegak lurus adalah berupa setengah putaran. Apakah hasil kali 2 pencerminan jika kedua sumbu sebarang? ? ?

Ambil sebarang sumbu s dan t yang berpotongan di P. Sebuah titik A sebarang dikenai Ms dan Mt , berarti : Ms(A) = A’ Mt(A’) = A’’ Jadi, Mt(A’) = A’’ Mt(Ms(A)) = A’’ (Mt • Ms)(A) =A’’ Ambil Q titik tengah AA’ Ambil R titik tengah A’A’’

DEFINISI Putaran terhadap P dengan sudut θ sebagai sudut putar dilambangkan dengan RP, θ adalah pemetaan yang memenuhi : ◦ RP, θ (P) = P ◦ Rp, θ (A) =A’ di mana PA=PA’ dan P = pusat putar θ = sudut putar

CATATAN Jika θ = 0 o maka RP, θ = I Jika θ = 180 o maka RP, θ = HP Jika α = β maka α = β + k • 360 o, dengan k anggota B+ Sudut θ positif jika arah berlawanan jarum jam

SIFAT Sebarang putaran RP, θ selalu dapat dianggap sebagai hasil kali 2 pencerminan, satu terhadap sumbu s dan satu terhadap sumbu t. P = titik (s, t) Jadi, hasil kali 2 pencerminan Mt • Ms : ◦ Jika s//t maka Mt • Ms = SAB dengan AB = 2 jarak (s, t) ◦ Jika s tidak sejajar t maka Mt • Ms = Rp, θ dengan P = titik (s, t) dan ◦ Jika s tegak lurus t maka Mt • Ms = RP, θ = HP

RUMUS PUTARAN Dengan pusat putar (0, 0)

RUMUS PUTARAN Dengan pusat putar P(a, b)

TUGAS

ISOMETRI

HASILKALI BEBERAPA ISOMETRI HASILKALI YANG DIBICARAKAN 1. REFLEKSI GESER 2. GESERAN DAN ROTASI 3. ROTASI DAN ROTASI

PENGERTIAN REFLEKSI GESER Definisi Misalkan s suatu garis dan AB suatu garis berarah dengan AB // s. Suatu refleksi geser G adalah pemetaan yang memenuhi G=Ms. SAB. . Teorema Misal s garis dan AB garis berarah. Jika s//AB , maka Ms. SAB = SABMs

. Teorema Suatu refleksi geser tidak mempunyai titik tetap. Satu-satunya garis tetap adalah sumbunya sendiri. Teorema Misal t suatu garis dan CD suatu garis berarah sedemikian sehingga CD tida tegak lurus t. Terdapat suatu refleksi geser G sedemikian sehingga G = SCDMt.

ilustrasi . D E r t C

. Misalkan p suatu garis dengan p // t dan jarak (p, t) = ½ |CE| Maka : SCDMt = SEDSCE Mt = SED (Mp Mt ) Mt = SED Mp (Mt Mt ) = SED Mp I = SED Mp = G ( = suatu refleksi geser karena p//ED )

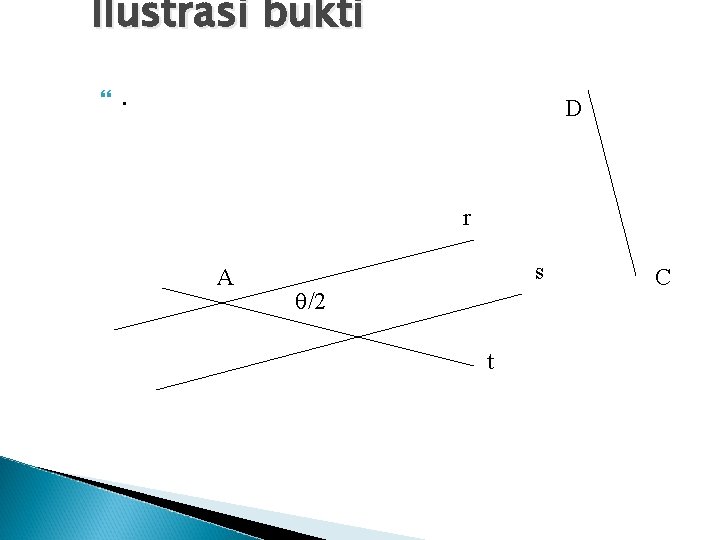
Teorema Misal s suatu garis dan A titik di luar s . Misalkan diketahui suatu sudut dengan besar . Terdapat suatu refleksi geser G 1 dan G 2 sedemikian sehingga G 1 = Ms RA, dan G 2 = RA, M s. ( Dengan kata lain teorema ini , mengatakan bahwa suatu putaran terhadap A dan diikuti oleh suatu refleksi terhadap garis s atau sebaliknya merupakan suatu refleksi geser )

Ilustrasi bukti . D r A s /2 t C

ukti Misalkan r garis yang melalui A dan r // s. Misalkan t garis yang melalui A dengan m(<(t, r)) = ½ . Diperoleh Ms RA, = Ms (Mr Mt) = (Ms Mr) Mt = SCD Mt = G 1.

orema Misalkan s suatu garis, P titik yang tidak terletak pada s. Misal r garis yang melalui P tegak lurus s. Maka berlaku: a. HPMs merupakan suatu refleksi geser yang sama dengan Mr. SAB b. Ms. HP merupakan suatu refleksi geser yang sama dengan SCDMr.

bukti . Misal t adalah garis yang melalui P dengan t // s dan r garis yang melalui P dengan r tegak lurus s. Misal AB garis berarah dengan AB//r , |AB| = 2 kali jarak (s, t) dan CD garis berarah dengan CD//r , |CD| = 2 kali jarak ( t, s). Sehingga HP Ms = ( Mr Mt ) Ms = Mr ( Mt Ms ) = Mr SAB Kemudian Ms HP = Ms ( Mt Mr ) = (Ms Mt ) Mr = SCD Mr

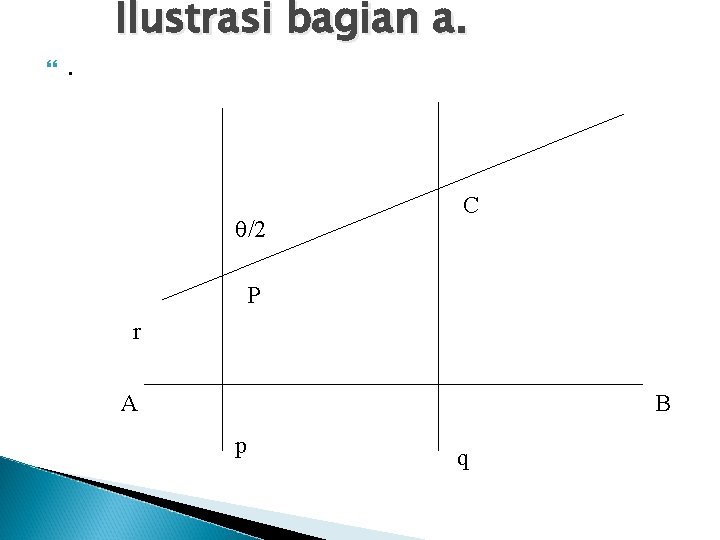
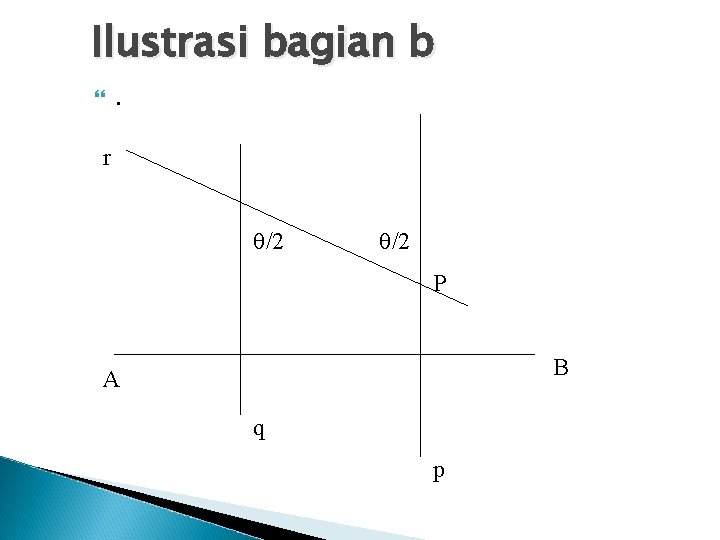
Geseran dan Putaran Teorema Untuk sebarang titik A, B, P dan suatu sudut dengan besar , selalu dapat ditemukan titik C dan D sedemikian sehingga : a. SAB RP, = RC, b. RP, SAB = RD,

. Ilustrasi bagian a. /2 C P r A B p q

Bukti . Dari yang diketahui titik-titik A, B, dan P serta suatu sudut dengan besar , tarik garis p melalui P dengan p tegak lurus AB dan tarik garis q dengan q // p , (p, q) = ½ |AB|. Kemudian buat garis r melalui P dengan m(<(r, p)) = ½ . Sehingga : SAB RP, = (Mq Mp )(Mp Mr ) = Mq ( Mp Mp ) Mr = Mq I Mr = Mq Mr = RC,

Ilustrasi bagian b . r /2 P B A q p

Bukti b. Dari yang diketahui titik-titik A, B, dan P serta suatu sudut dengan besar , tarik garis p melalui P dengan p tegak lurus AB dan tarik garis q dengan q // p , (p, q) = ½ |AB|. Kemudian buat garis r melalui P dengan m(<(p, r)) = ½ . RP, SAB = ( Mr Mp ) (Mp Mq ) = Mr( Mp Mp ) Mq = Mr I Mq = Mr Mq = RD,

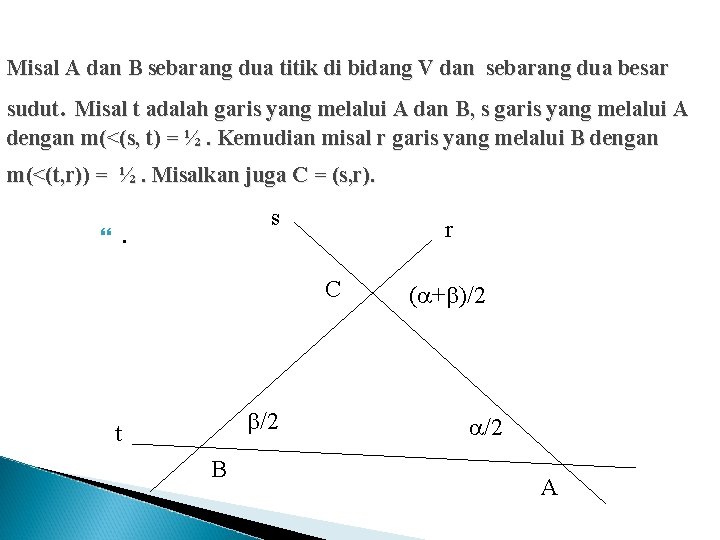
Putaran dan Putaran Pada saat membahas tentang putaran telah diketahui bahwa hasil kali dua putaran yang pusatnya sama , akan menghasilkan suatu putaran baru dengan pusat semula dan besar sudut putar adalah jumlah dari kedua sudut putar semula, atau dalam lambang putaran. Berikut ini akan dibahas tentang hasil kali putaran dengan putaran tetapi pusat kedua putaran tidak sama. Teorema Hasil kali dua putaran , A B akan berupa putaran lagi dengan sudut putar + atau berupa geseran jika + = 360.

Misal A dan B sebarang dua titik di bidang V dan sebarang dua besar sudut. Misal t adalah garis yang melalui A dan B, s garis yang melalui A dengan m(<(s, t) = ½. Kemudian misal r garis yang melalui B dengan m(<(t, r)) = ½. Misalkan juga C = (s, r). s . r C /2 t B ( + )/2 /2 A

. Dalam segitiga ABC di atas, m(<ABC) = m(<(t, r)) = ½ . dan m(<CAB) = m(<(s, t) = ½ , maka m(<ACD =(<(s, r)) = ½ + ½ = ( + )/2 , sehingga putaran yang dihasilkan oleh Mr. Ms mempunyai sudut putaran sebesar + .

. Hal tersebut tidak akan terjadi jika C tidak ada( yaitu dalam kondisi r // s). Jadi apabila m(<(r, t)) = m(<(s, t)) = ½ , tetapi m(<(t, r)) = -m(<(r, t)) = ½ . Jadi – ½ = ½ sehingga + = 0. Dalam hal ini RB, RA, = Mr. Ms = SCD ( dengan |CD| = 2 kali jarak ( s, r)

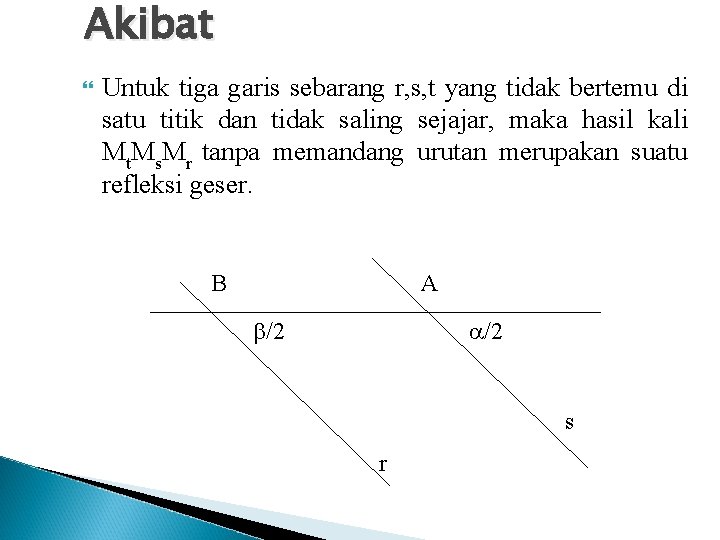
Akibat Untuk tiga garis sebarang r, s, t yang tidak bertemu di satu titik dan tidak saling sejajar, maka hasil kali Mt. Ms. Mr tanpa memandang urutan merupakan suatu refleksi geser. B A /2 s r

Bukti Pandang Mt. Ms. Mr = Mt (Ms. Mr ) = Mt RA, = G ( misal m(<(r, s)) = Apa yang terjadi jika r, s, t melalui satu titik yang sama ? Bagaimana pula jika r//t//s

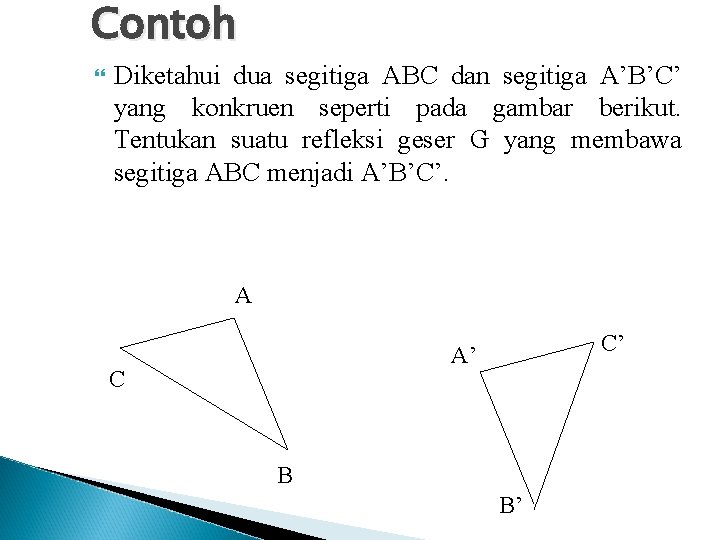
Contoh Diketahui dua segitiga ABC dan segitiga A’B’C’ yang konkruen seperti pada gambar berikut. Tentukan suatu refleksi geser G yang membawa segitiga ABC menjadi A’B’C’. A C’ A’ C B B’

Jawab Andaikan G sudah didapat, berarti terdapat ruas garis berarah PQ dan garis s sedemikian sehingga G = SPQMs yang berarti G(ABC) = A’B’C’. Misalkan A”B”C” = Ms(ABC) dan A’B’C’= SPQ(A”B”C”), diperoleh A’C’//A”C” dan m(<(s, AC)) = m(<(s, A”C”)). Jadi m(<(A’C’, s )) = m(<(s, AC)) . Sehingga dapat disimpulkan bahwa s sejajar dengan garis bagi (A’C’ , AC ).

Berdasarkan uraian tersebut , dapat diperoleh langkah dalam mendapatkan refleksi geser G. a. Lukis P = ( A’C’ , AC ) b. Lukis garis bagi <(A’C’ , AC ), yaitu garis t. c. Lukis garis m, dengan m//t , m melalui A dan garis l, dengan l t, l melalui A. Misal A”=( m, l ). d. Lukis garis s , dengan s//t dan s melalui titik tengah AA”. e. Lukis titik-titik B” dan C” , dengan B”=Ms(B) dan C”=Ms(C). f. Lukis titik P, Q di t sedemikian sehingga PQ=A’A” g. Diperoleh G= SPQMs sedemikian sehingga (A’B’C’) = SPQMs (ABC) = G(ABC)

SIMILARITAS (KESEBANGUNANAN)

Similaritas (kesebangunan)

Bukti Similaritas adalah suatu kolineasi