Geomecnica computacional Mdulo 2 Geotecnia III UNLP Geomecnica

Geomecánica computacional Módulo 2 Geotecnia III UNLP

Geomecánica computacional 2 Plasticidad perfecta unidimensional Ensayo de laboratorio 2 Interpretación Teoría

Plasticidad perfecta 1 D Geomecánica computacional 2 • Variables de estado 3 Son las variables independientes del problema Cuando uno conoce el valor de las variables de estado, sabe exactamente en que estado está el material

Geomecánica computacional 2 Plasticidad perfecta 1 D • Variables de estado • Cinemática de elastoplasticidad Es la hipótesis básica de la compatibilidad Esta simple fórmula implica que no hay deformaciones dependientes del tiempo 4

Geomecánica computacional 2 Plasticidad perfecta 1 D 5 • Variables de estado • Cinemática de elastoplasticidad • Relación tensión-deformación Permite calcular las tensiones conociendo sólo la parte elástica de las deformaciones

Geomecánica computacional 2 Plasticidad perfecta 1 D • • Variables de estado Cinemática de elastoplasticidad Relación tensión-deformación Función de fluencia Permite establecer cuando se produce la plasticidad (la “falla”) del material 6

Geomecánica computacional 2 Plasticidad perfecta 1 D • • Variables de estado Cinemática de elastoplasticidad Relación tensión-deformación Función de fluencia • Regla de flujo Permite establecer que dirección tendrán las deformaciones permanentes del material 7

Geomecánica computacional 2 Plasticidad perfecta 1 D El rol de la función de fluencia 8 • Si la tensión es menor a la tensión de fluencia, el comportamiento es elástico • La tensión no puede ser mayor que la tensión de fluencia • Si la tensión es igual a la tensión de fluencia, puede haber deformación plástica • La deformación plástica depende del trabajo aportado

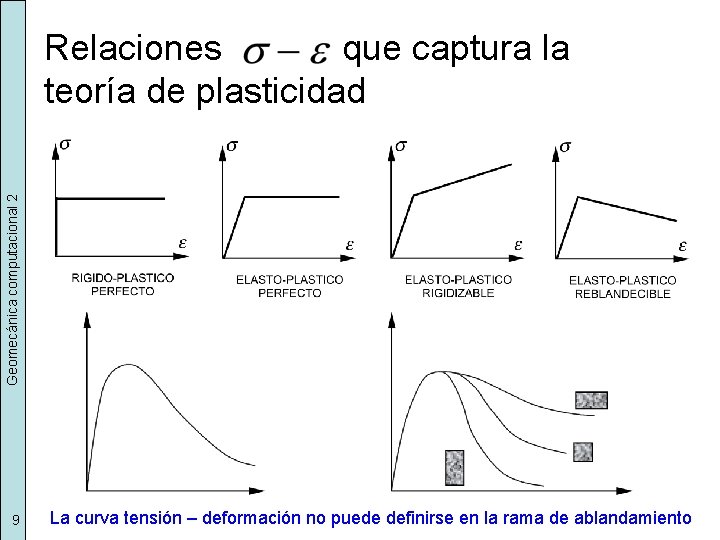
Geomecánica computacional 2 Relaciones que captura la teoría de plasticidad 9 La curva tensión – deformación no puede definirse en la rama de ablandamiento

Geomecánica computacional 2 Elementos de un modelo elastoplástico general • • Variables de estado Cinemática de elastoplasticidad Relación tensión-deformación Función de fluencia • Regla de flujo • Reglas de evolución (en la plasticidad con endurecimiento/ablandamiento) 10

Geomecánica computacional 2 Plasticidad perfecta El rol de la regla de flujo 11 • La regla de flujo indica para donde es la deformación plástica (en 1 D es sólo la función signo) • En plasticidad 3 D, la regla de flujo determina la dirección de la deformación plástica • G es una función escalar, lo que implica que los autovectores de son los mismos que los de

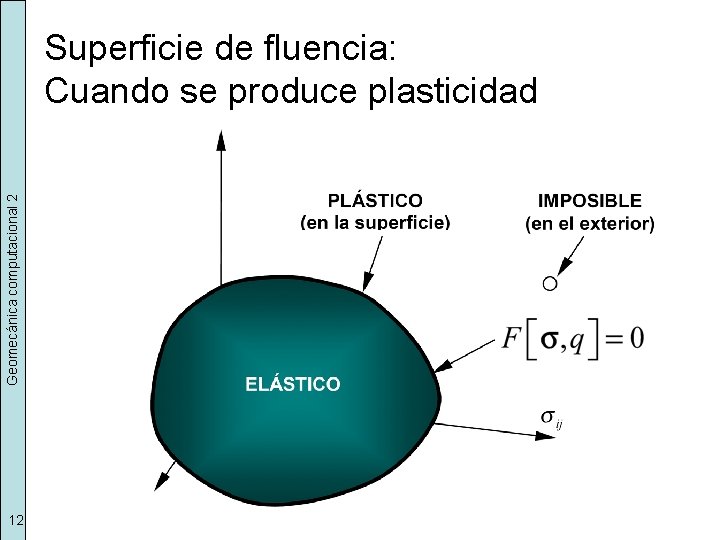
Geomecánica computacional 2 Superficie de fluencia: Cuando se produce plasticidad 12

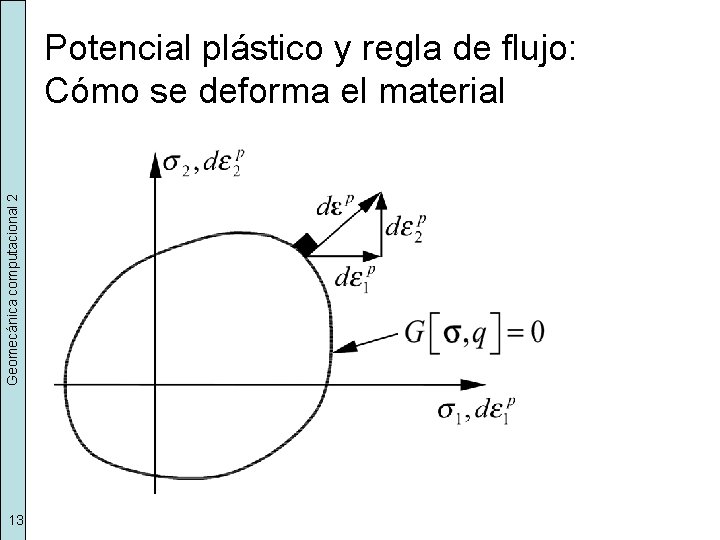
Geomecánica computacional 2 Potencial plástico y regla de flujo: Cómo se deforma el material 13

Geomecánica computacional 2 Asociatividad plástica 14 Asociatividad (típica en metales) No asociatividad (típica en materiales friccionales) La no-asociatividad de los materiales friccionales está asociada a la componente volumétrica de la deformación plástica (ejemplo mas adelante)

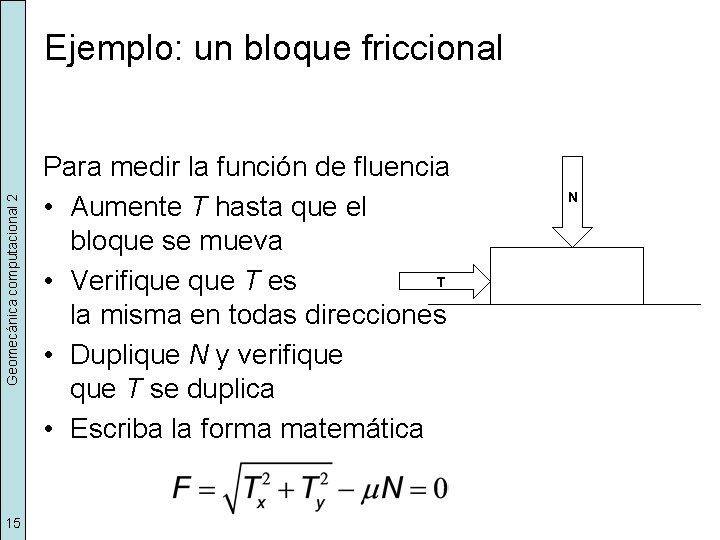
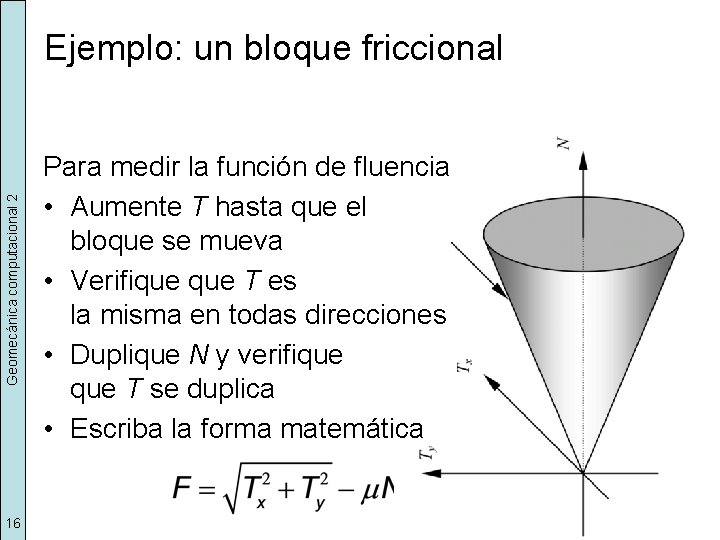
Geomecánica computacional 2 Ejemplo: un bloque friccional 15 Para medir la función de fluencia • Aumente T hasta que el bloque se mueva T • Verifique T es la misma en todas direcciones • Duplique N y verifique T se duplica • Escriba la forma matemática N

Geomecánica computacional 2 Ejemplo: un bloque friccional 16 Para medir la función de fluencia • Aumente T hasta que el bloque se mueva • Verifique T es la misma en todas direcciones • Duplique N y verifique T se duplica • Escriba la forma matemática

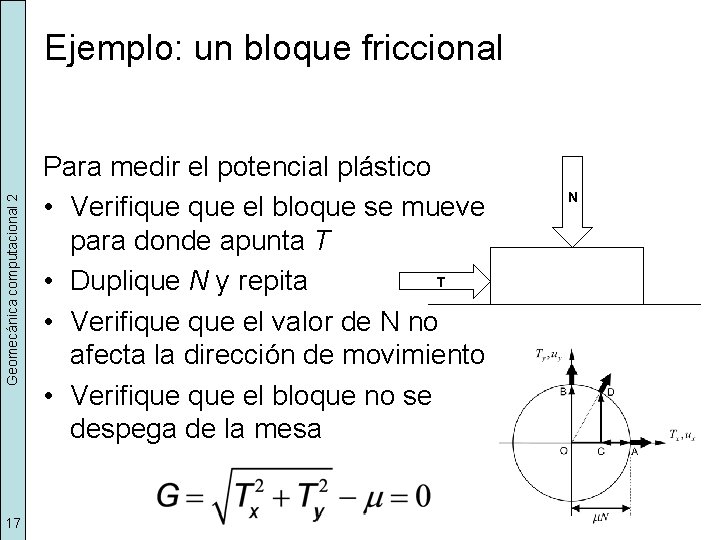
Geomecánica computacional 2 Ejemplo: un bloque friccional 17 Para medir el potencial plástico • Verifique el bloque se mueve para donde apunta T T • Duplique N y repita • Verifique el valor de N no afecta la dirección de movimiento • Verifique el bloque no se despega de la mesa N

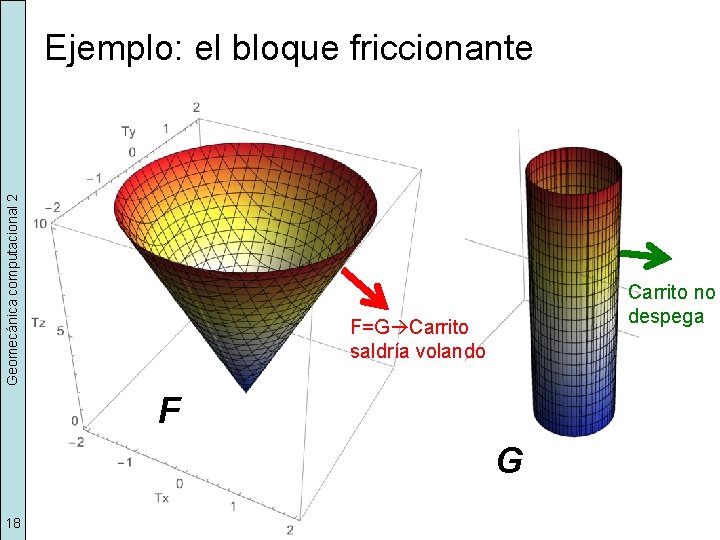
Geomecánica computacional 2 Ejemplo: el bloque friccionante Carrito no despega F=G Carrito saldría volando F G 18

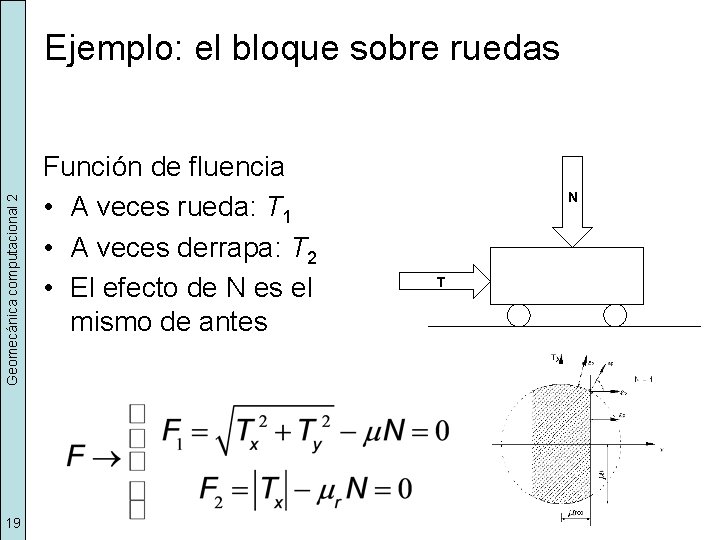
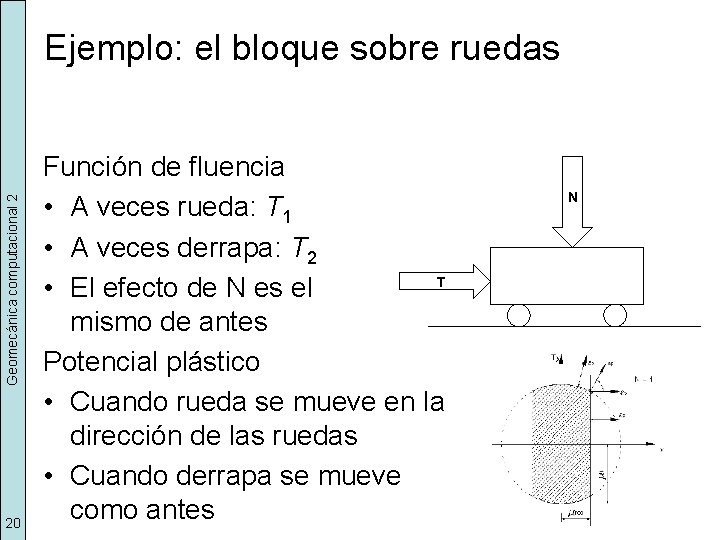
Geomecánica computacional 2 Ejemplo: el bloque sobre ruedas 19 Función de fluencia • A veces rueda: T 1 • A veces derrapa: T 2 • El efecto de N es el mismo de antes N T

Geomecánica computacional 2 Ejemplo: el bloque sobre ruedas 20 Función de fluencia • A veces rueda: T 1 • A veces derrapa: T 2 T • El efecto de N es el mismo de antes Potencial plástico • Cuando rueda se mueve en la dirección de las ruedas • Cuando derrapa se mueve como antes N

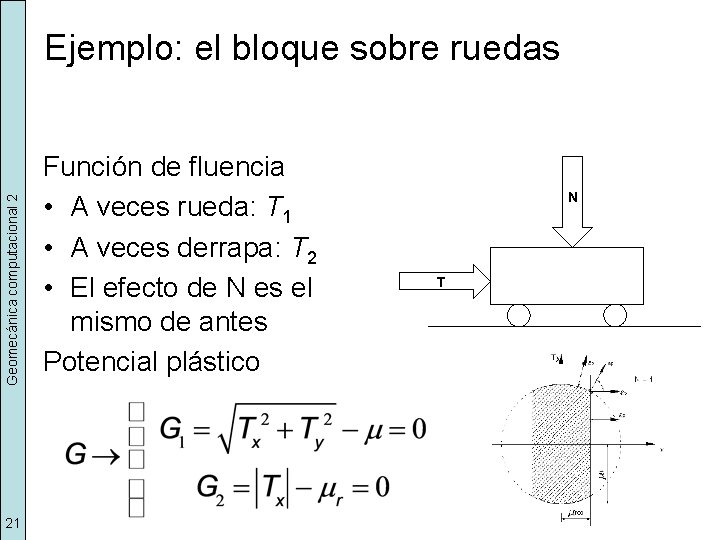
Geomecánica computacional 2 Ejemplo: el bloque sobre ruedas 21 Función de fluencia • A veces rueda: T 1 • A veces derrapa: T 2 • El efecto de N es el mismo de antes Potencial plástico N T

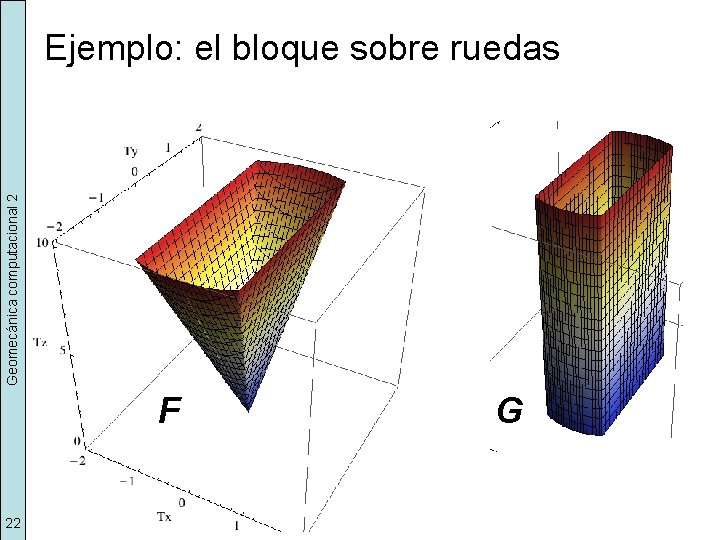
Geomecánica computacional 2 Ejemplo: el bloque sobre ruedas F 22 G

Ejemplo: cómputo del desplazamiento (fórmulas) Geomecánica computacional 2 Cinemática Relación cargadesplazamiento Función de fluencia Potencial plástico Trabajo aplicado 23

Ejemplo: cómputo del desplazamiento (datos entrada) Geomecánica computacional 2 Cinemática 24 Relación cargadesplazamiento Función de fluencia Potencial plástico Se impone un desplazamiento horizontal de 10 cm ¿cuánto trabajo se aporta, cuanto se almacena y cuanto se consume?

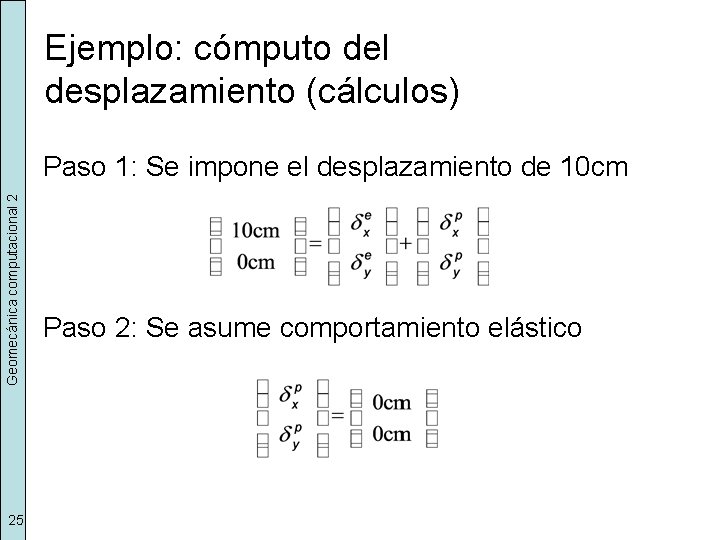
Ejemplo: cómputo del desplazamiento (cálculos) Geomecánica computacional 2 Paso 1: Se impone el desplazamiento de 10 cm 25 Paso 2: Se asume comportamiento elástico

Ejemplo: cómputo del desplazamiento (cálculos) Geomecánica computacional 2 Paso 3: Se calcula la fuerza resultante Paso 4: Se verifica el criterio de fluencia Como F > 0 habrá desplazamiento plástico 26

Ejemplo: cómputo del desplazamiento (cálculos) Geomecánica computacional 2 Paso 5: Se calcula la dirección de despl. plástico 27 Paso 6: Se calcula el multiplicador plástico λ

Ejemplo: cómputo del desplazamiento (cálculos) Geomecánica computacional 2 Paso 7: Se calculan los desplazamientos finales Paso 8: Se calcula el trabajo realizado Respuesta: Trabajo total = 4. 38 k. Nm; Almacenado = 0. 63 k. Nm; Disipado = 3. 75 k. Nm 28

Geomecánica computacional 2 Comportamiento que captura la plasticidad perfecta La plasticidad perfecta fue desarrollada para aceros (rigidez constante, tensión de fluencia constante) • Criterio de Tresca • Criterio de Von Mises 29 (Hoyos 2012)

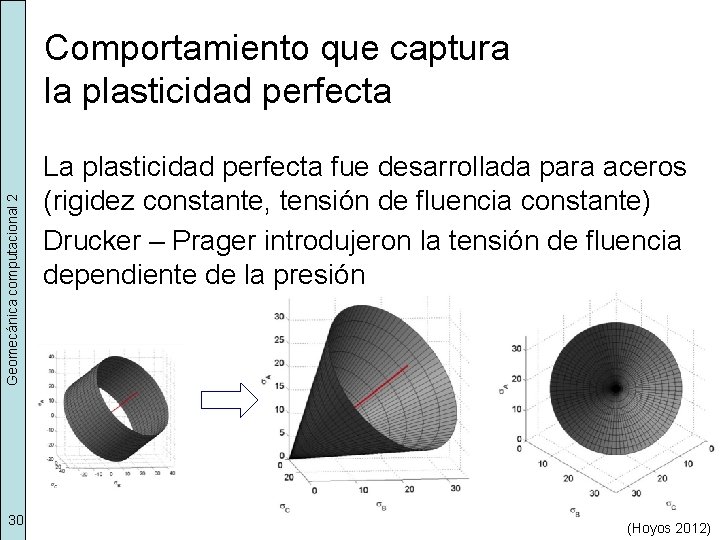
Geomecánica computacional 2 Comportamiento que captura la plasticidad perfecta 30 La plasticidad perfecta fue desarrollada para aceros (rigidez constante, tensión de fluencia constante) Drucker – Prager introdujeron la tensión de fluencia dependiente de la presión (Hoyos 2012)

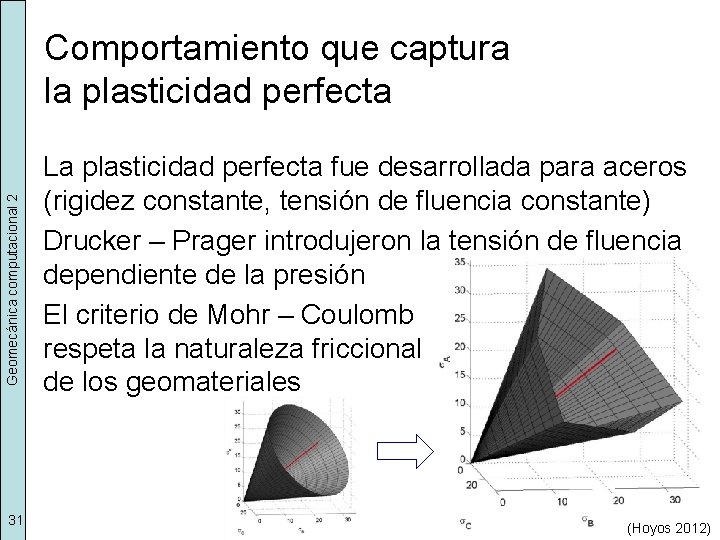
Geomecánica computacional 2 Comportamiento que captura la plasticidad perfecta 31 La plasticidad perfecta fue desarrollada para aceros (rigidez constante, tensión de fluencia constante) Drucker – Prager introdujeron la tensión de fluencia dependiente de la presión El criterio de Mohr – Coulomb respeta la naturaleza friccional de los geomateriales (Hoyos 2012)

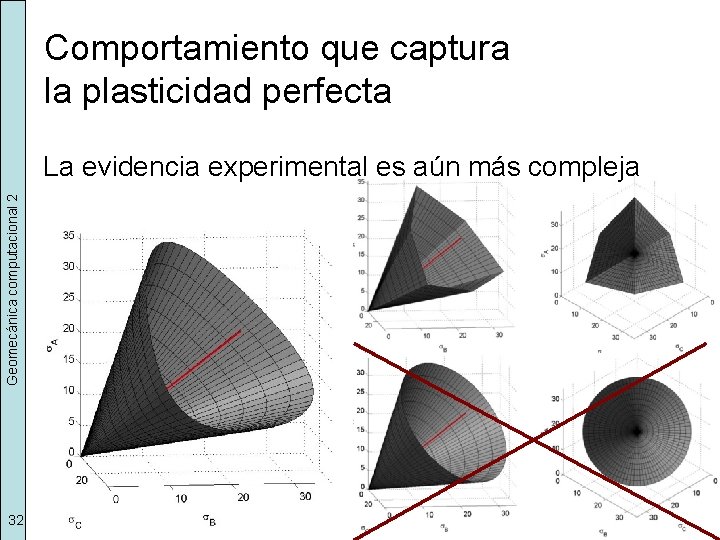
Comportamiento que captura la plasticidad perfecta Geomecánica computacional 2 La evidencia experimental es aún más compleja 32

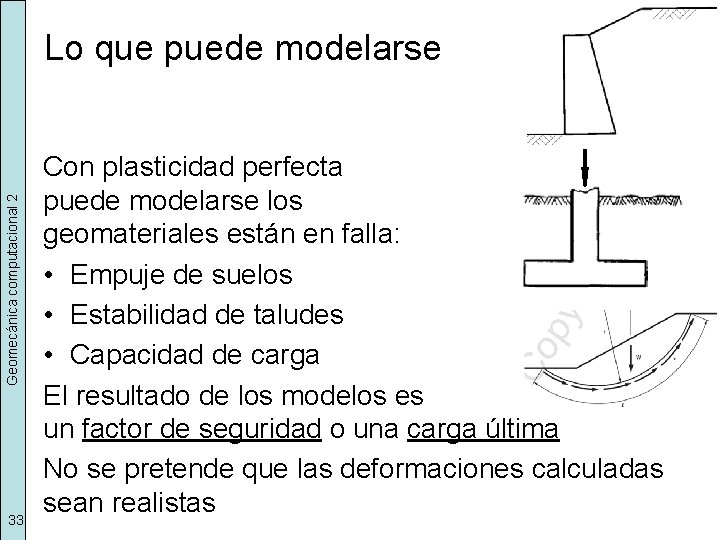
Geomecánica computacional 2 Lo que puede modelarse 33 Con plasticidad perfecta puede modelarse los geomateriales están en falla: • Empuje de suelos • Estabilidad de taludes • Capacidad de carga El resultado de los modelos es un factor de seguridad o una carga última No se pretende que las deformaciones calculadas sean realistas

Geomecánica computacional 2 Lo que no debe modelarse 34 No debe modelarse problemas de interacción suelo – estructura o aquellos en los que la deformación controla el comportamiento: • Asentamiento de fundaciones • Túneles (excepto seguridad del frente) • Compresión y consolidación • Problemas acoplados (p. ej. no drenado) Si se requiere una predicción de desplazamientos y/o solicitaciones estructurales conviene emplear plasticidad con endurecimiento

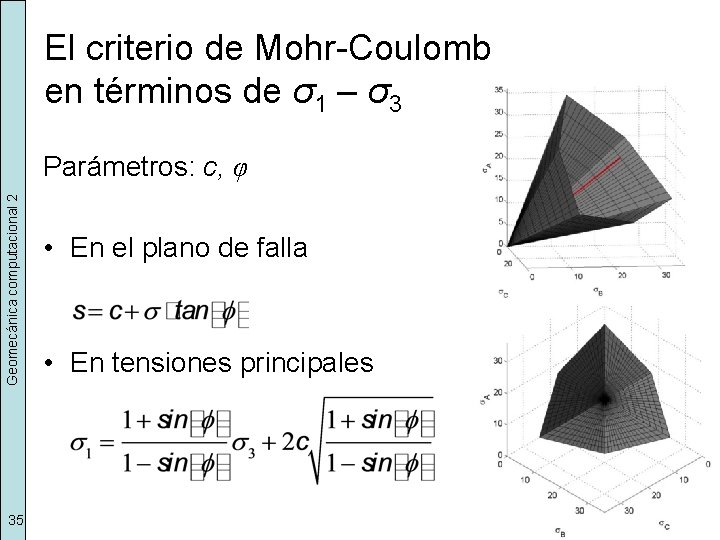
El criterio de Mohr-Coulomb en términos de σ1 – σ3 Geomecánica computacional 2 Parámetros: c, φ 35 • En el plano de falla • En tensiones principales

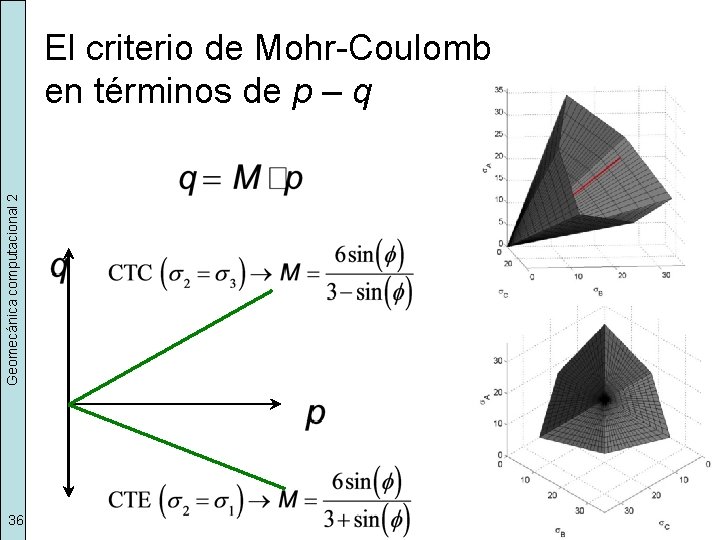
Geomecánica computacional 2 El criterio de Mohr-Coulomb en términos de p – q 36

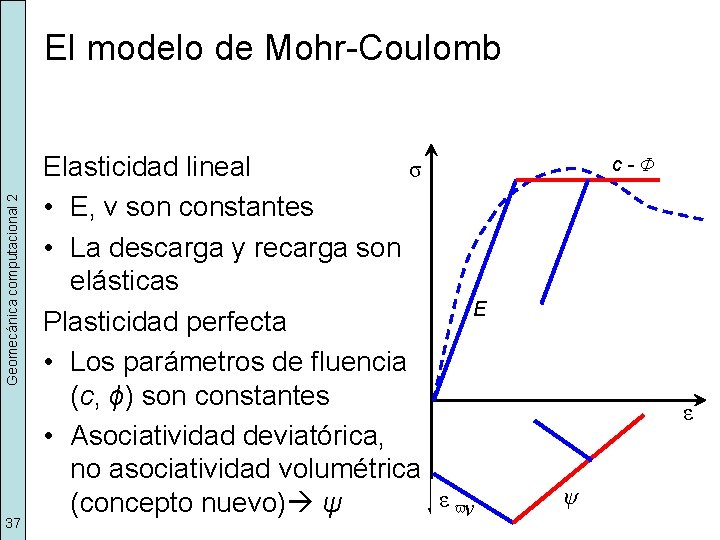
Geomecánica computacional 2 El modelo de Mohr-Coulomb 37 Elasticidad lineal σ • E, ν son constantes • La descarga y recarga son elásticas E Plasticidad perfecta • Los parámetros de fluencia (c, ϕ) son constantes • Asociatividad deviatórica, no asociatividad volumétrica ε vν (concepto nuevo) ψ c-Φ ε ψ

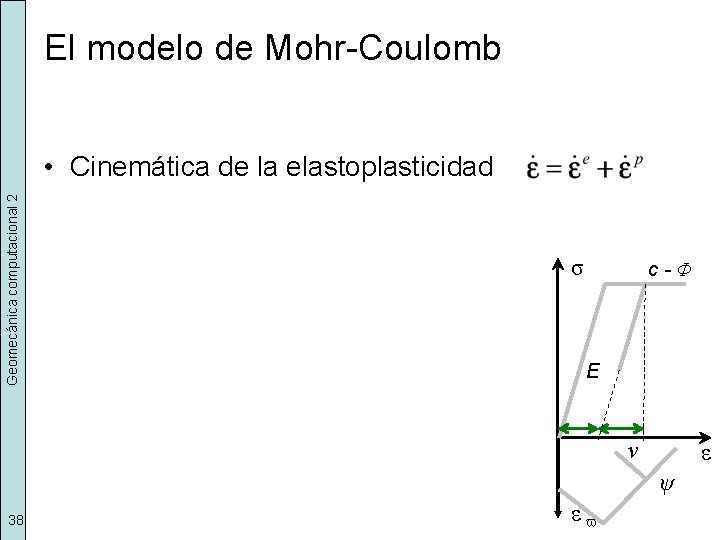
El modelo de Mohr-Coulomb Geomecánica computacional 2 • Cinemática de la elastoplasticidad σ c-Φ E ν ε ψ 38 εv

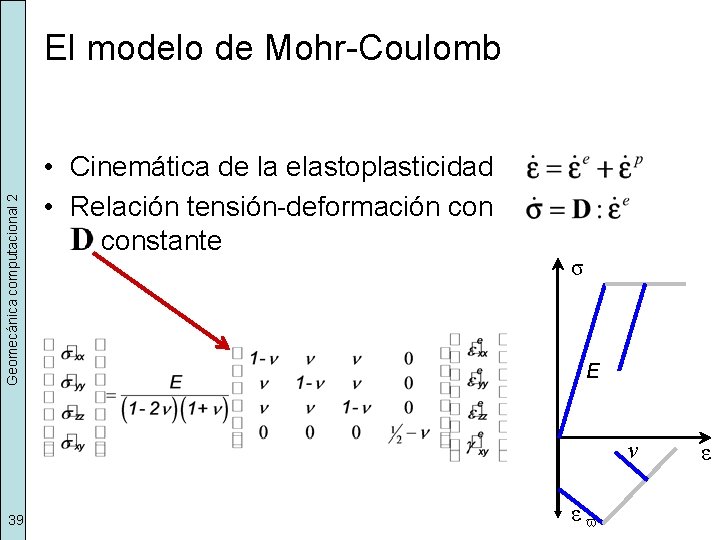
Geomecánica computacional 2 El modelo de Mohr-Coulomb • Cinemática de la elastoplasticidad • Relación tensión-deformación constante σ E ν 39 εv ε

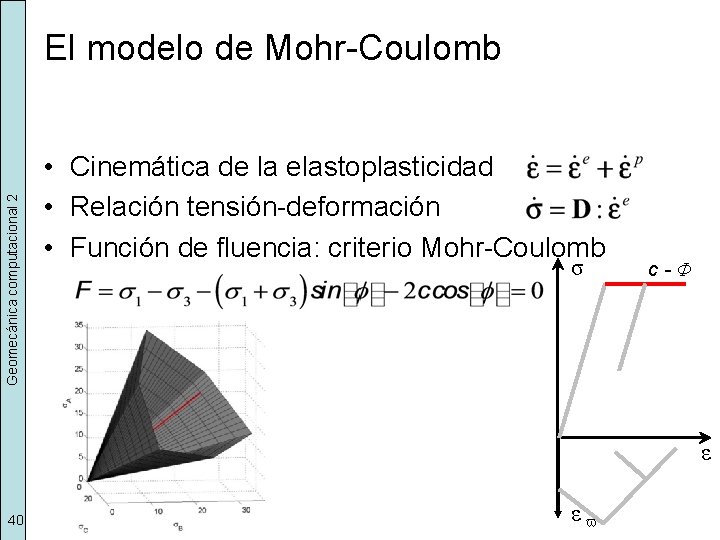
Geomecánica computacional 2 El modelo de Mohr-Coulomb • Cinemática de la elastoplasticidad • Relación tensión-deformación • Función de fluencia: criterio Mohr-Coulomb σ c-Φ ε 40 εv

Geomecánica computacional 2 El modelo de Mohr-Coulomb • • Cinemática de la elastoplasticidad Relación tensión-deformación Función de fluencia Ley de flujo (ángulo de dilatancia que controla el cambio de volumen durante la deformación plástica) σ ε ψ 41 εv

Geomecánica computacional 2 El modelo de Mohr-Coulomb Resumen 42 • • Cinemática de la elastoplasticidad Relación tensión-deformación Función de fluencia Ley de flujo • Noten la similitud formal entre F y G

Geomecánica computacional 2 Ventajas y limitaciones del modelo de Mohr-Coulomb 43 Ventajas • Modelo simple y claro • Buena representación de falla drenada • Comparable con resultados analíticos Desventajas • Elástico lineal hasta falla con rigidez constante • No distingue carga primaria de recarga • Predice comportamiento elástico en compresión edométrica

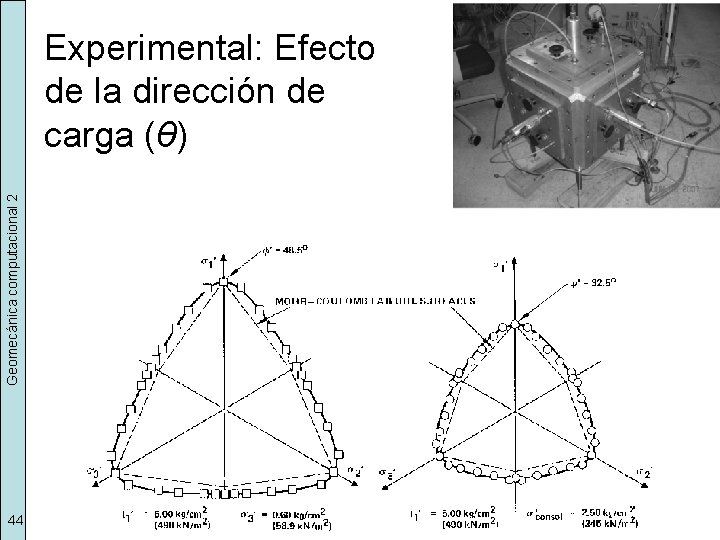
Geomecánica computacional 2 Experimental: Efecto de la dirección de carga (θ) 44

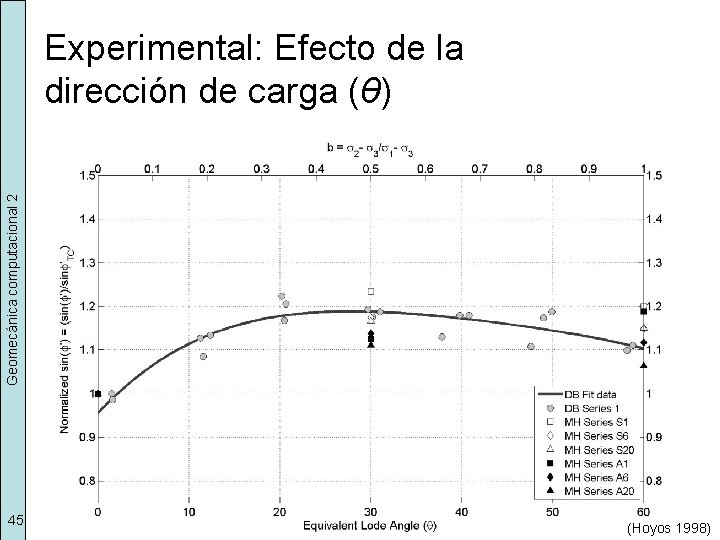
Geomecánica computacional 2 Experimental: Efecto de la dirección de carga (θ) 45 (Hoyos 1998)

Geomecánica computacional 2 Efecto de la dirección de carga en arenas (θ) 46

Geomecánica computacional 2 Efecto de la dirección de carga en arcillas (θ) 47

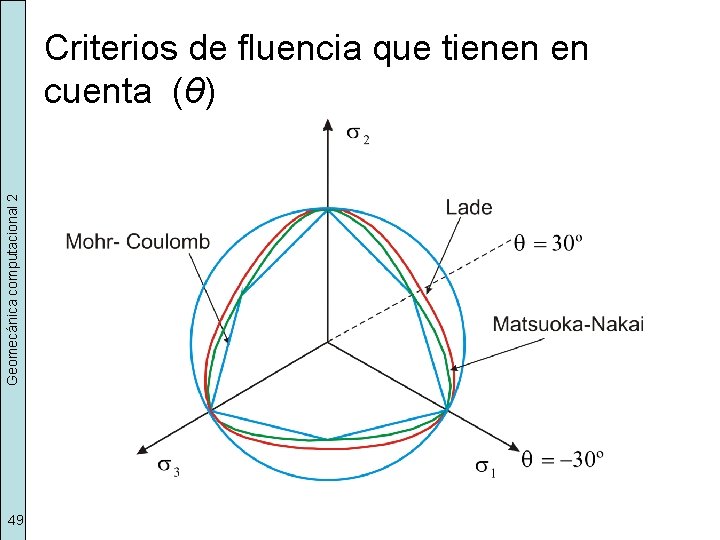
Criterios de fluencia que tienen en cuenta (θ) Geomecánica computacional 2 • Matsuoka – Nakai • Lade • Zienkiewicz – Pande 48

Geomecánica computacional 2 Criterios de fluencia que tienen en cuenta (θ) 49

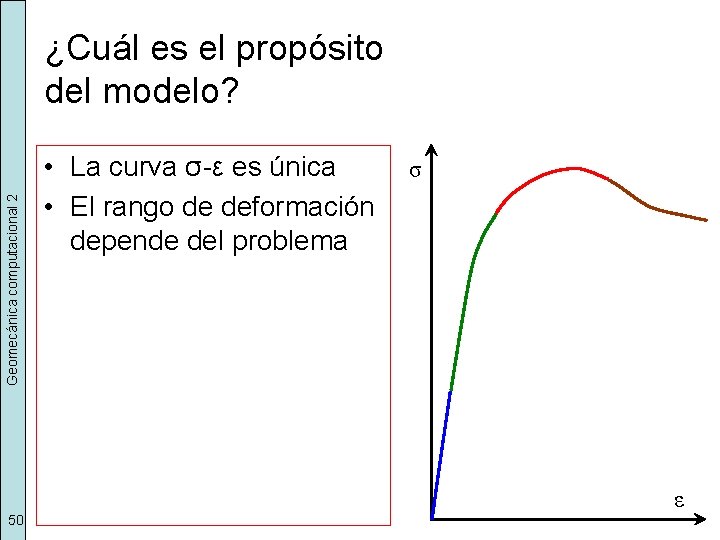
Geomecánica computacional 2 ¿Cuál es el propósito del modelo? • La curva σ-ε es única • El rango de deformación depende del problema σ ε 50

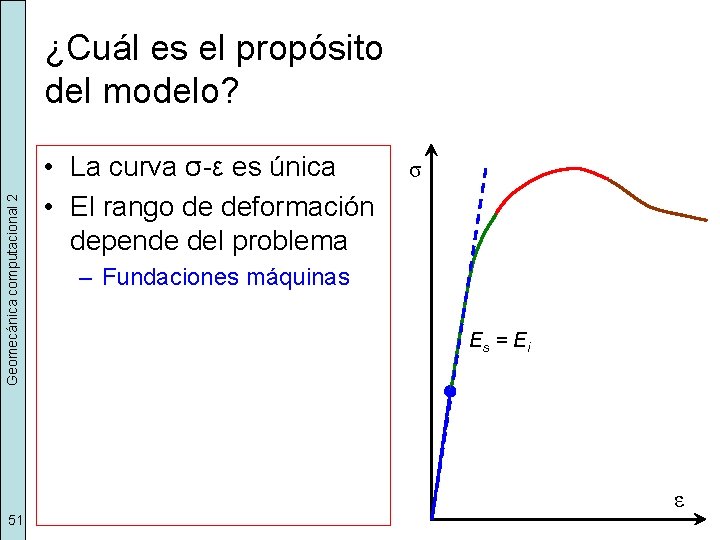
Geomecánica computacional 2 ¿Cuál es el propósito del modelo? • La curva σ-ε es única • El rango de deformación depende del problema σ – Fundaciones máquinas Es = E i ε 51

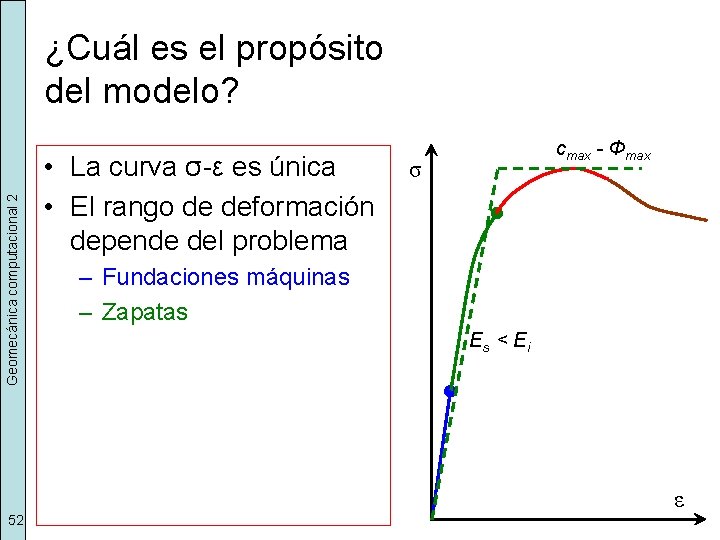
Geomecánica computacional 2 ¿Cuál es el propósito del modelo? • La curva σ-ε es única • El rango de deformación depende del problema cmax - Φmax σ – Fundaciones máquinas – Zapatas Es < E i ε 52

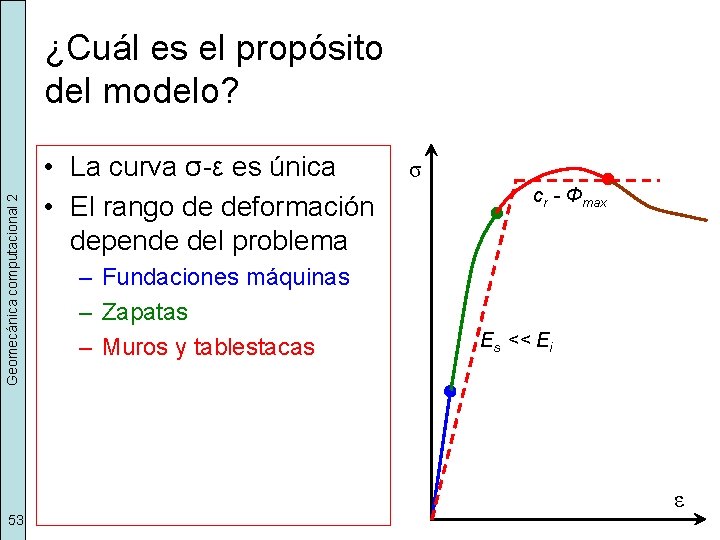
Geomecánica computacional 2 ¿Cuál es el propósito del modelo? • La curva σ-ε es única • El rango de deformación depende del problema – Fundaciones máquinas – Zapatas – Muros y tablestacas σ cr - Φmax Es << Ei ε 53

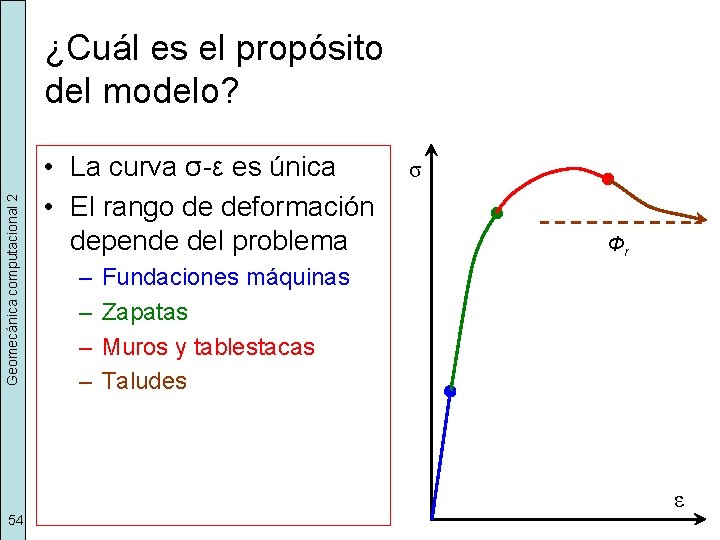
Geomecánica computacional 2 ¿Cuál es el propósito del modelo? • La curva σ-ε es única • El rango de deformación depende del problema – – σ Φr Fundaciones máquinas Zapatas Muros y tablestacas Taludes ε 54

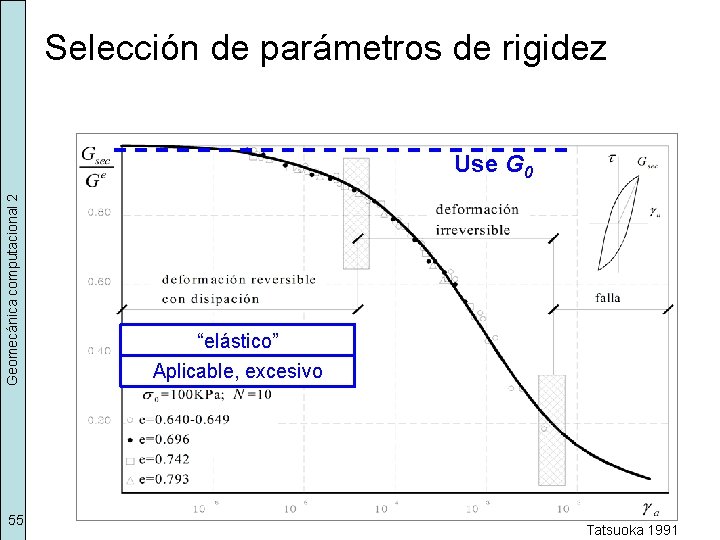
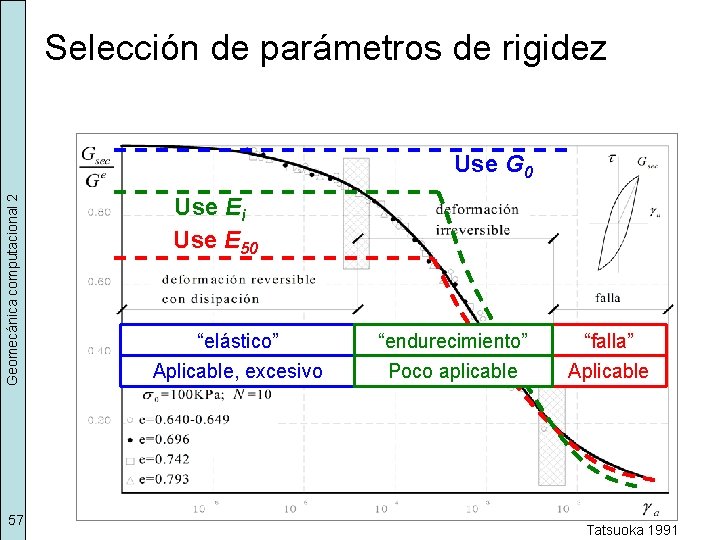
Selección de parámetros de rigidez Geomecánica computacional 2 Use G 0 55 “elástico” Aplicable, excesivo Tatsuoka 1991

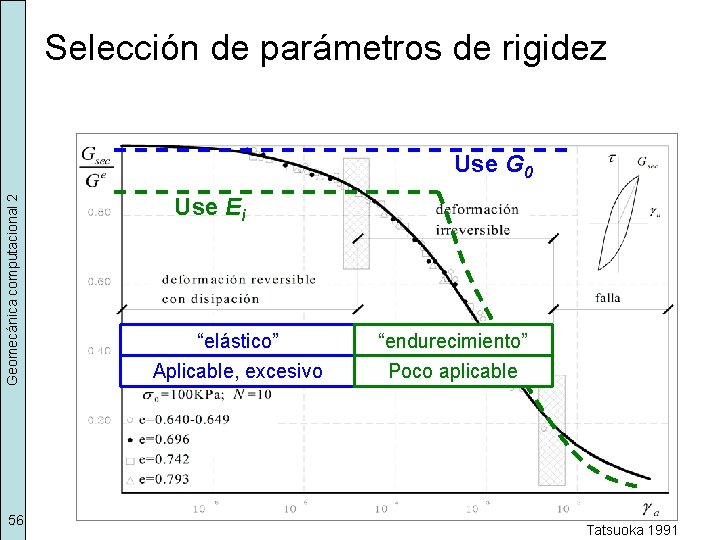
Selección de parámetros de rigidez Geomecánica computacional 2 Use G 0 56 Use Ei “elástico” “endurecimiento” Aplicable, excesivo Poco aplicable Tatsuoka 1991

Selección de parámetros de rigidez Geomecánica computacional 2 Use G 0 57 Use Ei Use E 50 “elástico” “endurecimiento” “falla” Aplicable, excesivo Poco aplicable Aplicable Tatsuoka 1991

Geomecánica computacional 2 Selección de parámetros resistentes 58 La selección de la cohesión y fricción debe tener en cuenta • El rango de deformación – Pequeñas deformaciones: use valores máximos – Grandes deformaciones: use valores residuales • La dirección de carga para M – C(los criterios J 3 lo tienen en cuenta explícitamente) • La presión media (si el modelo no lo tiene en cuenta explícitamente)

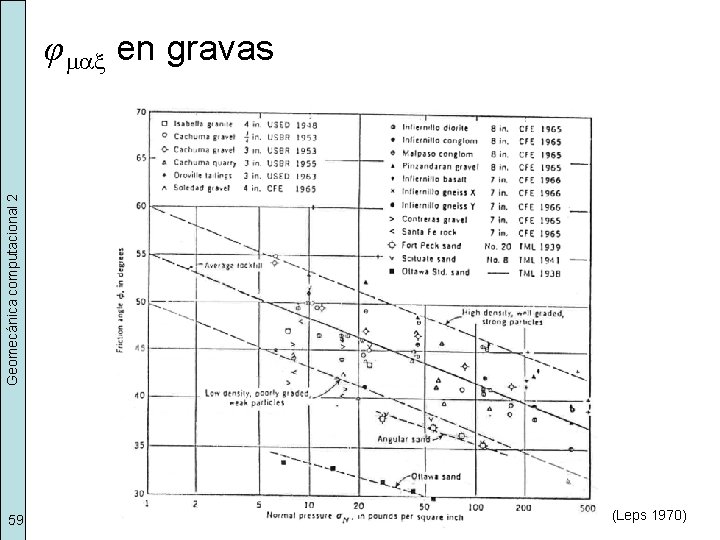
Geomecánica computacional 2 φ max en gravas 59 (Leps 1970)

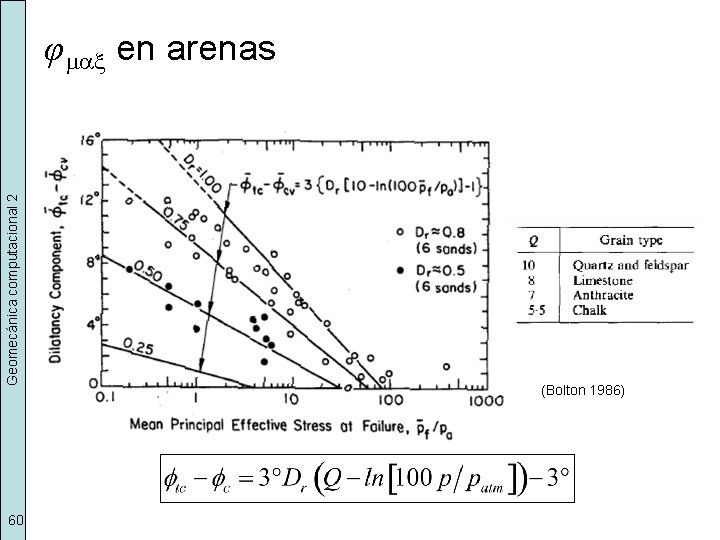
Geomecánica computacional 2 φ max en arenas 60 (Bolton 1986)

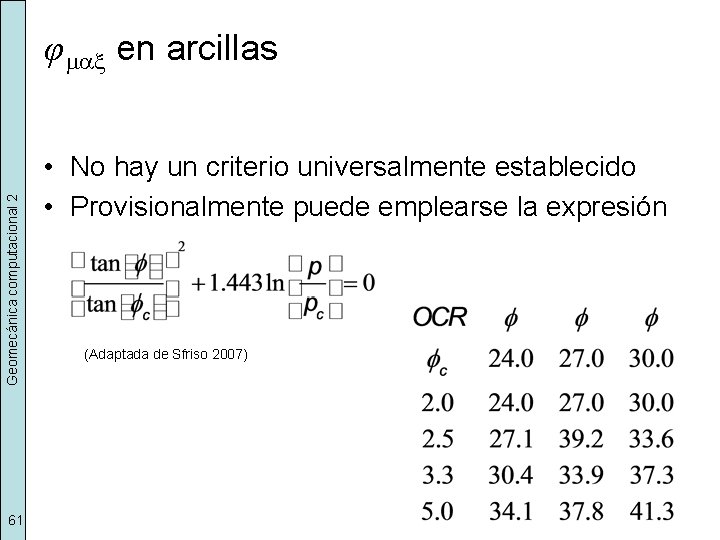
Geomecánica computacional 2 φ max en arcillas 61 • No hay un criterio universalmente establecido • Provisionalmente puede emplearse la expresión (Adaptada de Sfriso 2007)

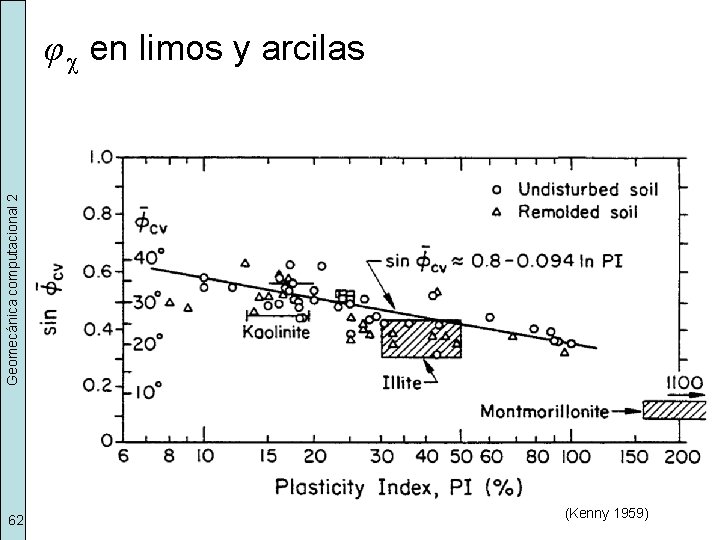
Geomecánica computacional 2 φ c en limos y arcilas 62 (Kenny 1959)

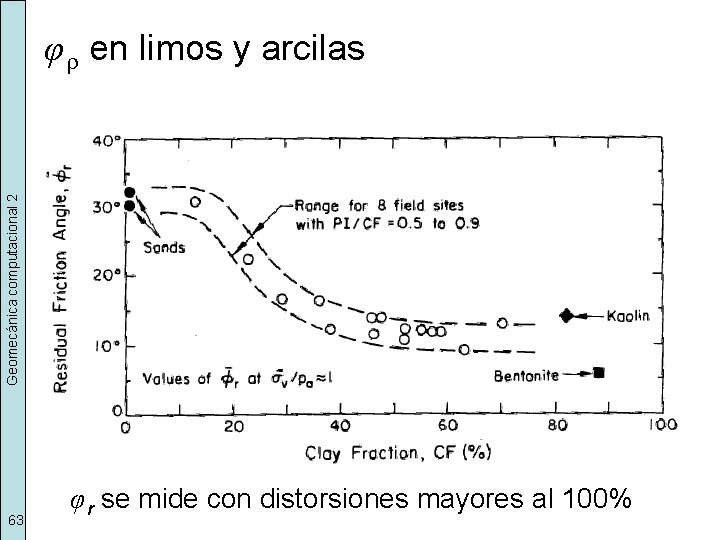
Geomecánica computacional 2 φ r en limos y arcilas 63 φ r se mide con distorsiones mayores al 100%

Geomecánica computacional 2 Arena/PP 64 Arena/PP es un modelo de plasticidad isotrópica • F = Matsuoka – Nakai • G = Teoría tensión – dilatancia de Rowe • Ángulo de fricción ϕ(p, e 0) = ϕc + ψ(p, e 0) El endurecimiento aparece porque el cambio de relación de vacíos impone un cambio de resistencia La dilatancia reduce la resistencia = ablandamiento plástico = localización de deformaciones La cadena se corta en el eslabón mas débil

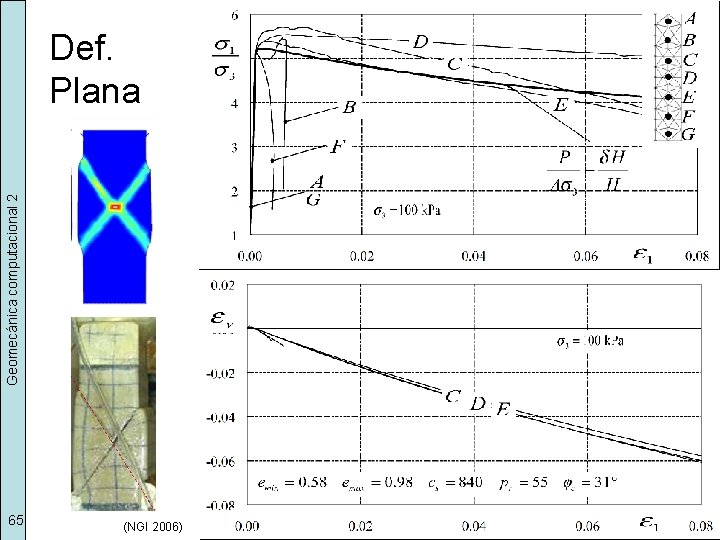
Geomecánica computacional 2 Def. Plana 65 (NGI 2006)

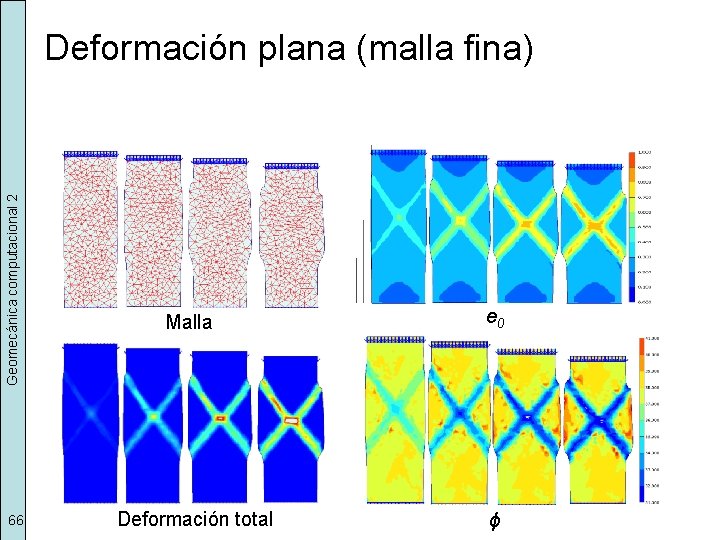
Geomecánica computacional 2 Deformación plana (malla fina) 66 Malla e 0 Deformación total ϕ

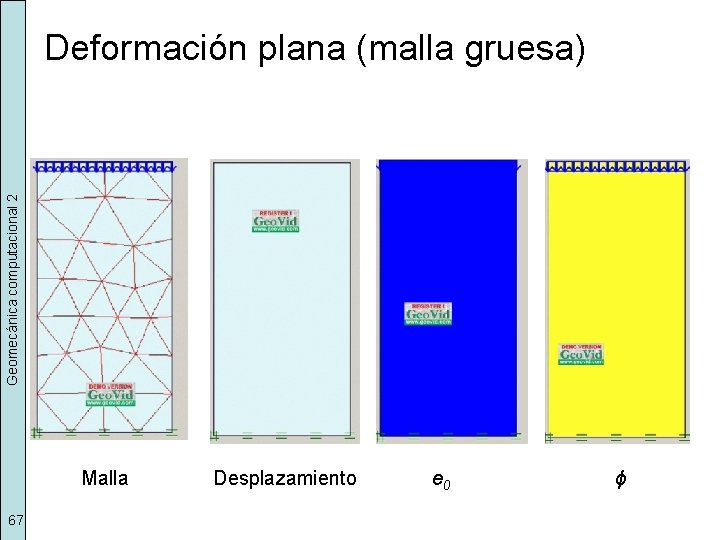
Geomecánica computacional 2 Deformación plana (malla gruesa) Malla 67 Desplazamiento e 0 ϕ

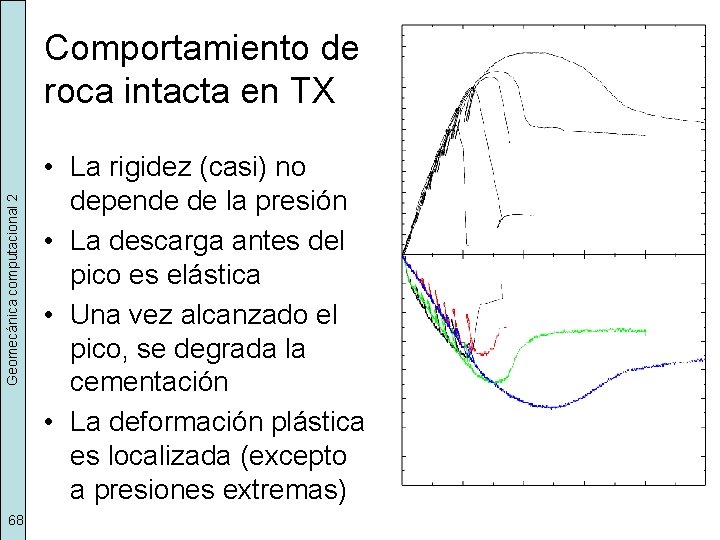
Geomecánica computacional 2 Comportamiento de roca intacta en TX 68 • La rigidez (casi) no depende de la presión • La descarga antes del pico es elástica • Una vez alcanzado el pico, se degrada la cementación • La deformación plástica es localizada (excepto a presiones extremas)

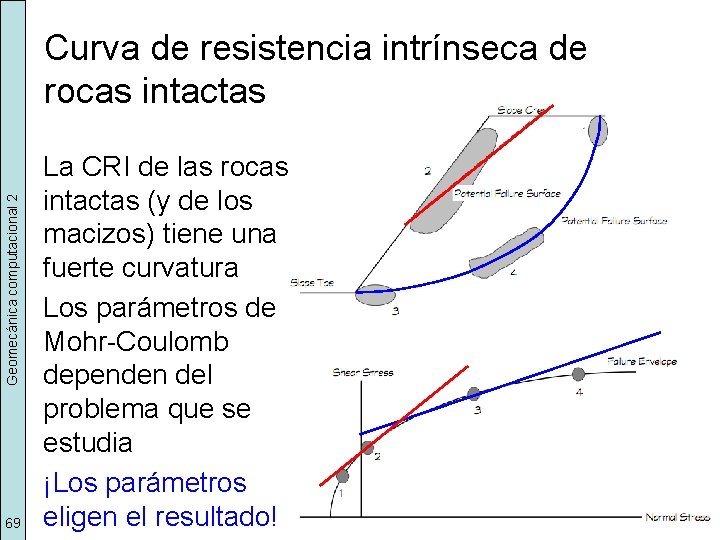
Geomecánica computacional 2 Curva de resistencia intrínseca de rocas intactas 69 La CRI de las rocas intactas (y de los macizos) tiene una fuerte curvatura Los parámetros de Mohr-Coulomb dependen del problema que se estudia ¡Los parámetros eligen el resultado!

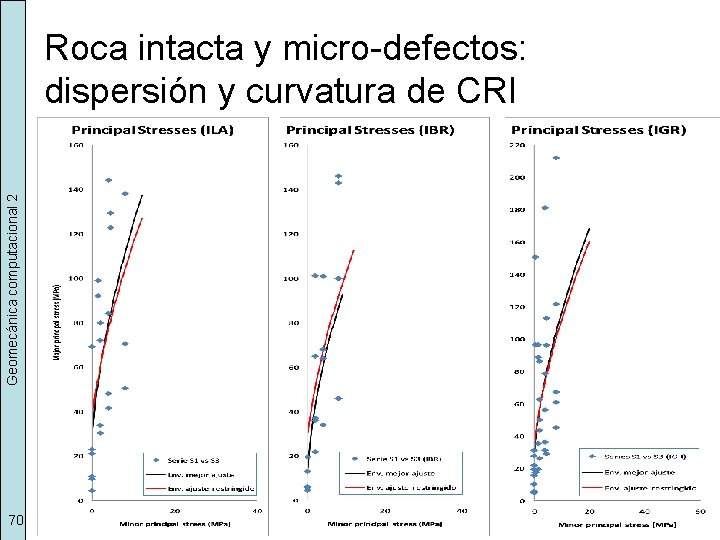
Geomecánica computacional 2 Roca intacta y micro-defectos: dispersión y curvatura de CRI 70

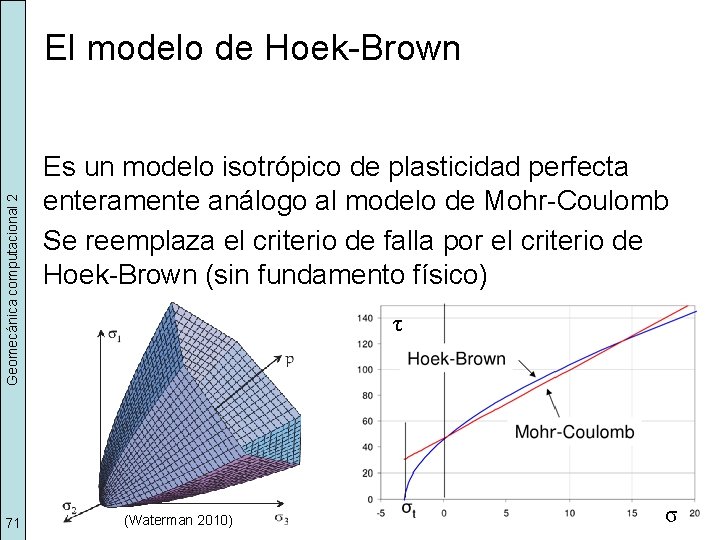
Geomecánica computacional 2 El modelo de Hoek-Brown 71 Es un modelo isotrópico de plasticidad perfecta enteramente análogo al modelo de Mohr-Coulomb Se reemplaza el criterio de falla por el criterio de Hoek-Brown (sin fundamento físico) τ (Waterman 2010) σ

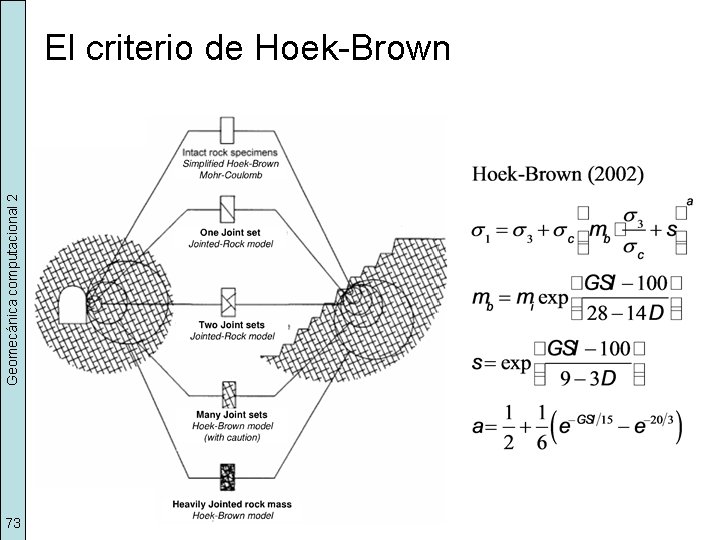
Geomecánica computacional 2 El criterio de Hoek-Brown 72 Limitaciones • Asume igual resistencia en todas las direcciones • Los parámetros dependen del grado de fracturamiento • Cambian todos los parámetros cuando cambia el grado de fracturación del macizo

Geomecánica computacional 2 El criterio de Hoek-Brown 73

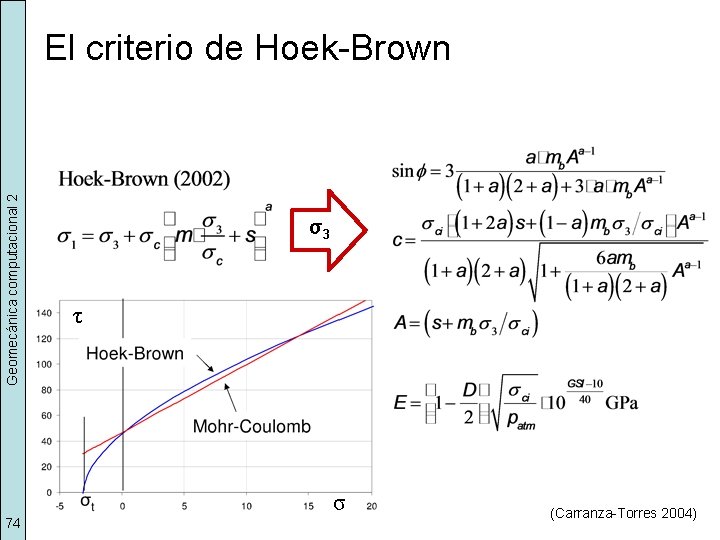
Geomecánica computacional 2 El criterio de Hoek-Brown 74 σ3 τ σ (Carranza-Torres 2004)

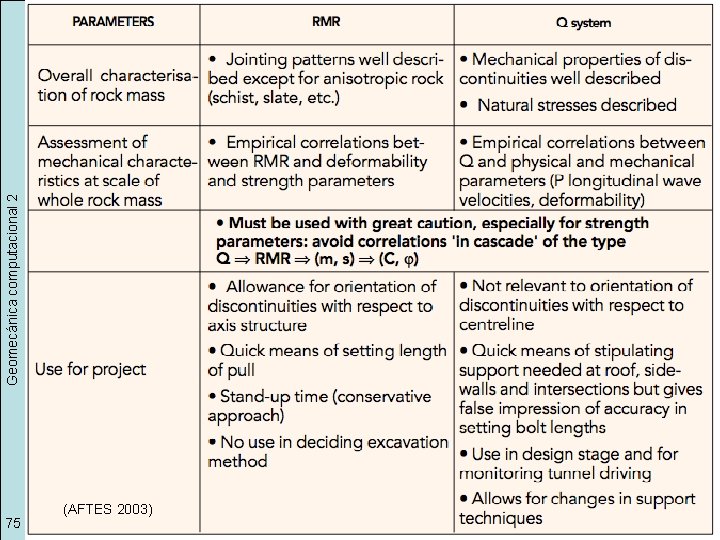
75 (AFTES 2003) Geomecánica computacional 2

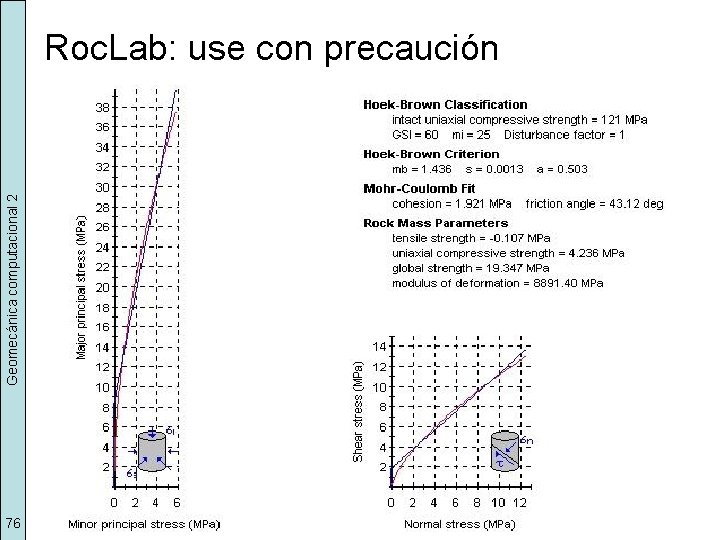
Geomecánica computacional 2 Roc. Lab: use con precaución 76

Geomecánica computacional 2 Ventajas y limitaciones del modelo de Hoek-Brown 77 Ventajas • Criterio de falla curvo, mejor ajuste que Mohr – Coulomb para rocas y macizos rocosos • Amplia aceptación por parte de la industria • Determinación de parámetros bien establecida Limitaciones • No tiene un buen fundamento físico • Plasticidad isotrópica • Calibración con GSI: falsa sensación de robustez

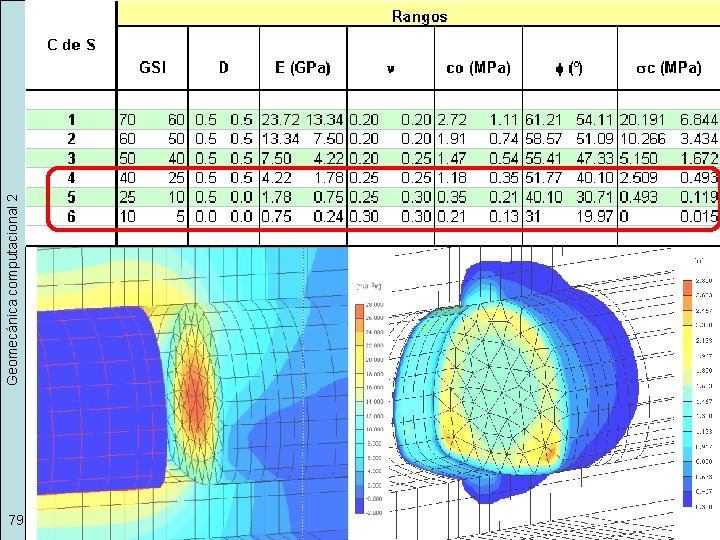
Geomecánica computacional 2 Los parámetros deben escalarse para el tamaño del problema 78

79 Geomecánica computacional 2

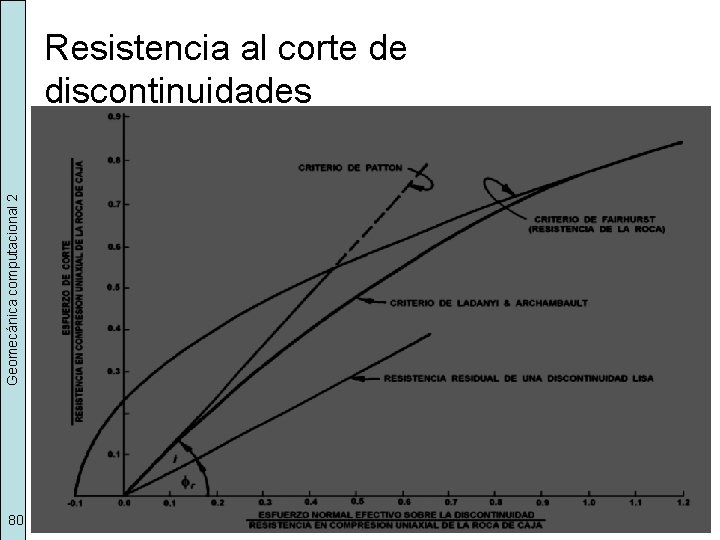
Geomecánica computacional 2 Resistencia al corte de discontinuidades 80

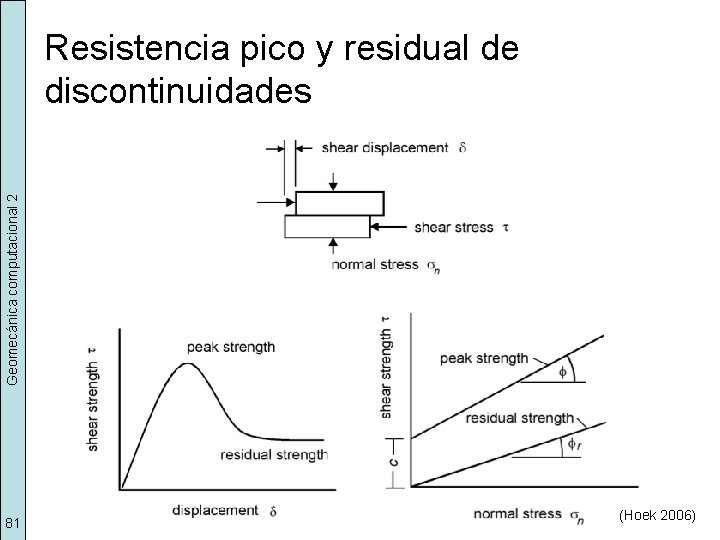
Geomecánica computacional 2 Resistencia pico y residual de discontinuidades 81 (Hoek 2006)

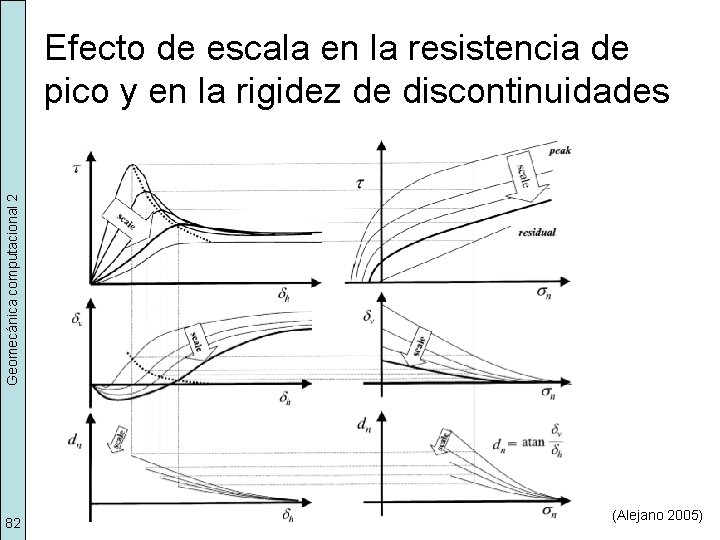
Geomecánica computacional 2 Efecto de escala en la resistencia de pico y en la rigidez de discontinuidades 82 (Alejano 2005)

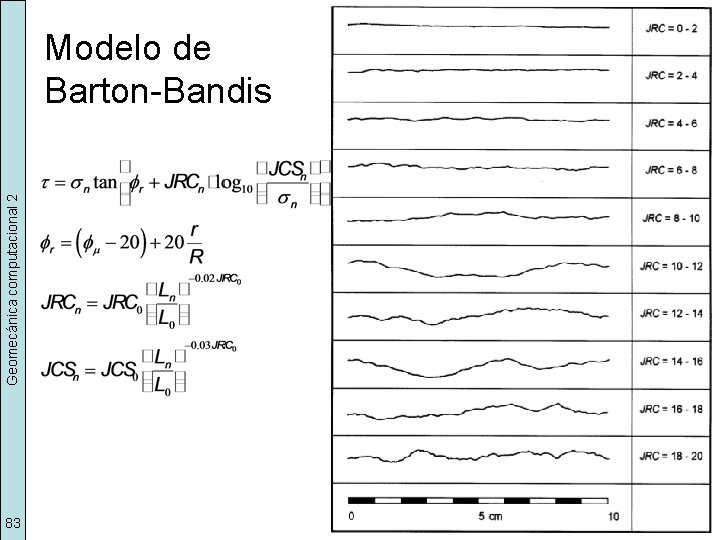
Geomecánica computacional 2 Modelo de Barton-Bandis 83

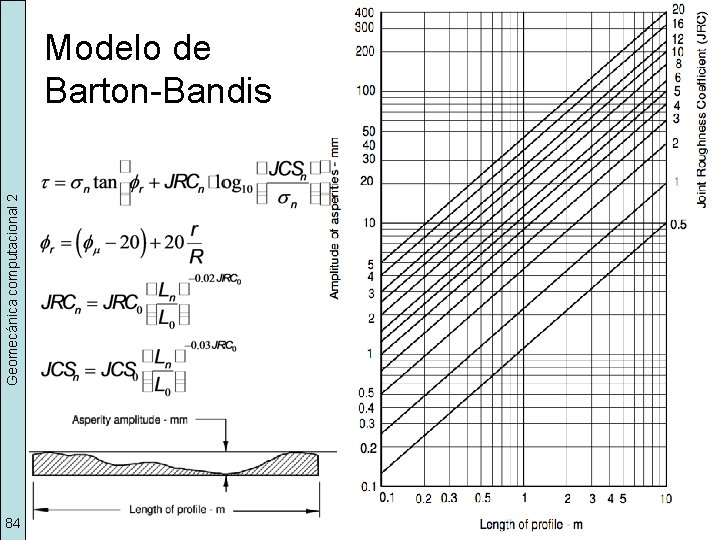
Geomecánica computacional 2 Modelo de Barton-Bandis 84

Criterios de Jennings y Cording-Jamil Geomecánica computacional 2 Jennings: interpolación lineal Lj Lr Lj Cording-Jamil: falla escalonada tan i=d/Lj Lj d Lj 85

Geomecánica computacional 2 Criterios de Jennings y Cording-Jamil: validación experimental 86 (Prudencio y Hormazábal 2012)

Geomecánica computacional 2 Bibliografía esencial (en orden decreciente) 87 • Potts et al. Guideline for the use of advanced numerical analysis. COST Action C 7. Thomas Telford 2002. • Potts & Zdravkovic. Finite element analysis in geotechnical engineering. Thomas Telford 1999. • Chen & Mizuno. Nonlinear analysis in soil mechanics. Elsevier 1990. • Muir Wood. Geotechnical modelling. 2004. • USACE. Geotechnical analysis by the FEM. Report ETL 1110 -2 -544. • Puzrin. Constitutive modelling in geomechanics. Springer 2012. • Yu. Plasticity and geotechnics. Springer 2006. • Bull. Numerical analysis modelling geomechanics. Spon Press 2003.

Geomecánica computacional 2 Bibliografía esencial (en orden decreciente) 88 • Bull. Numerical analysis modelling geomechanics. Spon Press 2003. • Zienkiewicz et al. Computational geomechanics. Wiley 1999. • Lewis&Schrefler. The FEM in the static and dynamic deformation and consolidation of porous media. Wiley 1998. • Bathe, K. Finite element procedures. Bathe. • Zienkiewicz et al. The finite element method. Butterworth-Heinemann. • Olivella & Agelet. Mecánica de medios continuos para ingenieros. UPC.