Geology Department Geophysics I Lecture 4 Isostasy theory

Geology Department Geophysics (I) Lecture 4

Isostasy theory Isostasy is the state of gravitational equilibrium between Earth's crust and mantle such that the crust "floats" at an elevation that depends on its thickness and density. Long wavelength variations in topography are isostatically compensated at depth. This means that the excess mass in positive topography is compensated by a mass deficiency at depth. There are three Models of Isostasy.

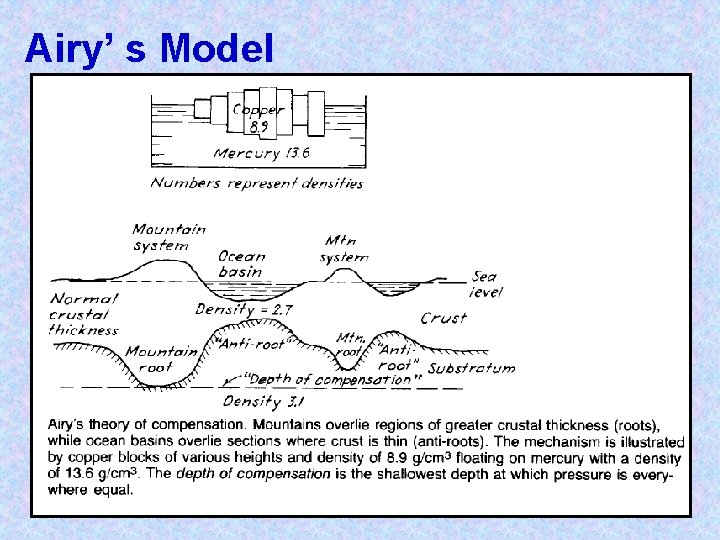
Airy’ s Model

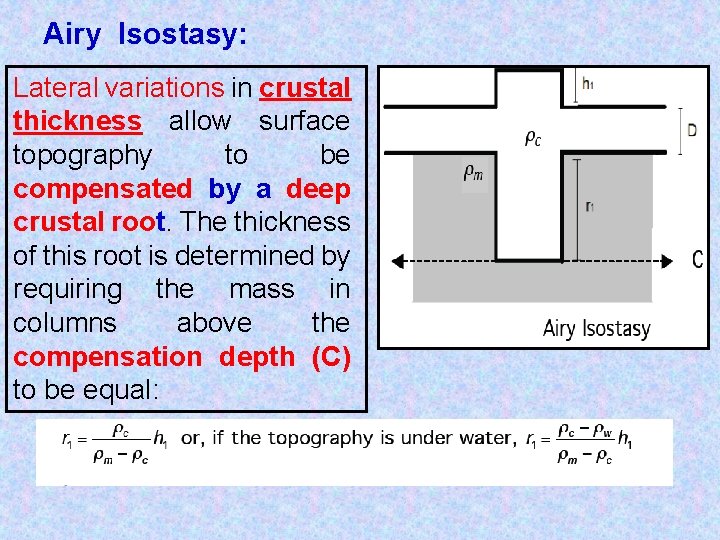
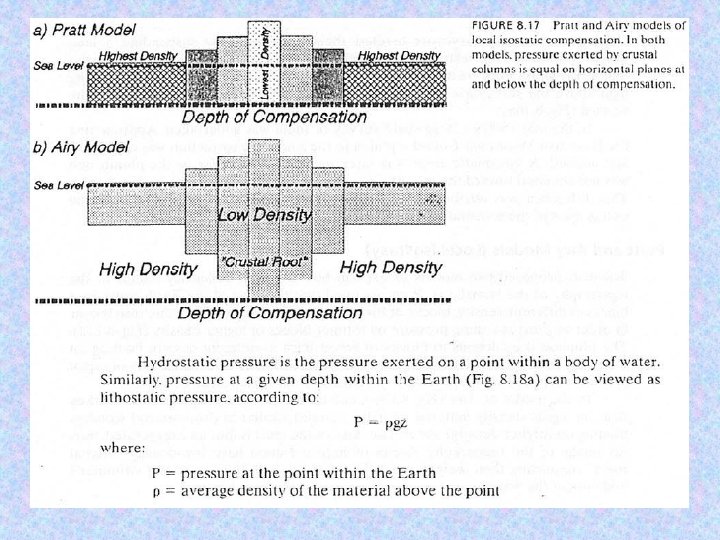
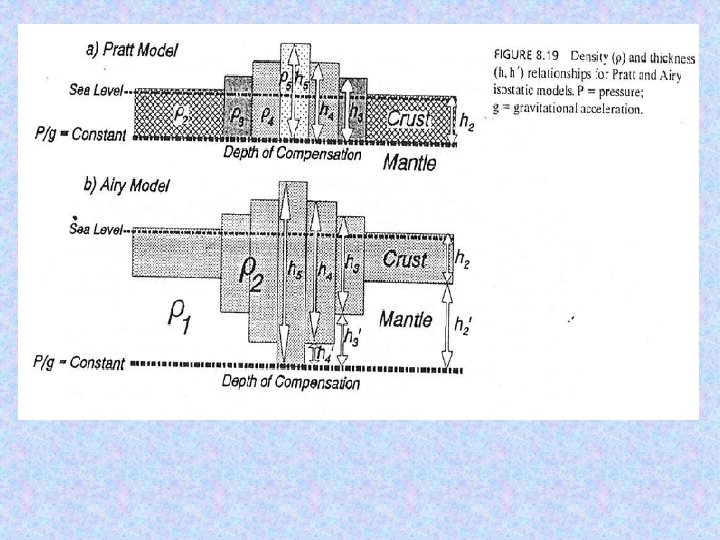
Airy Isostasy: Lateral variations in crustal thickness allow surface topography to be compensated by a deep crustal root. The thickness of this root is determined by requiring the mass in columns above the compensation depth (C) to be equal:

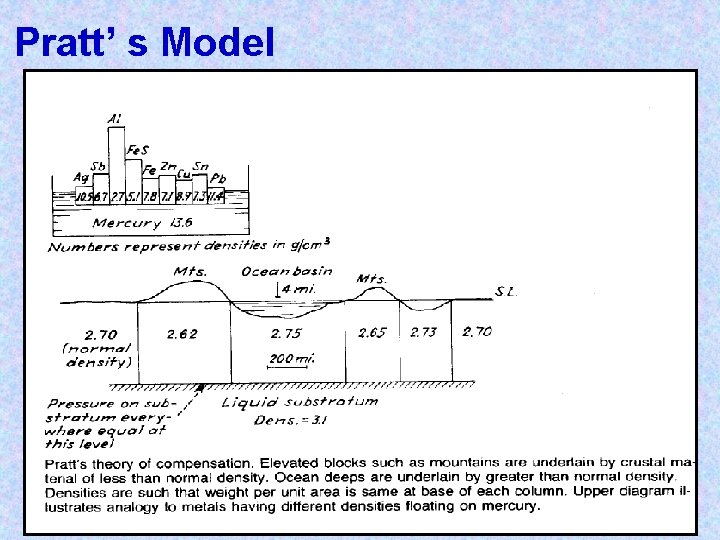
Pratt’ s Model

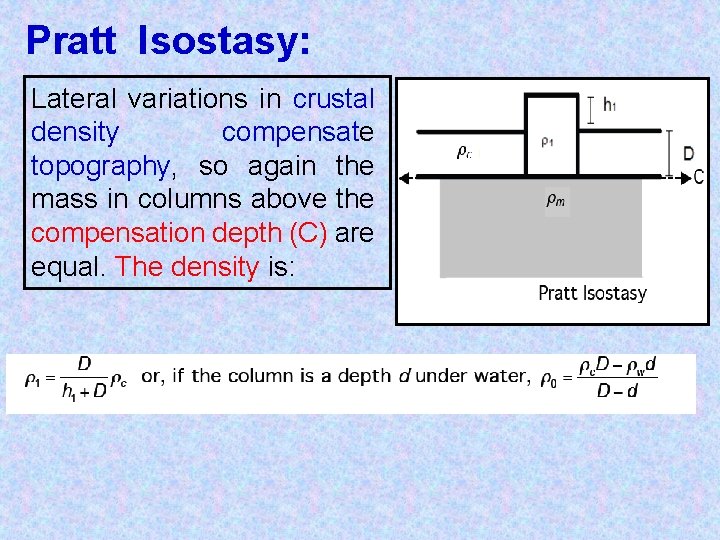
Pratt Isostasy: Lateral variations in crustal density compensate topography, so again the mass in columns above the compensation depth (C) are equal. The density is:

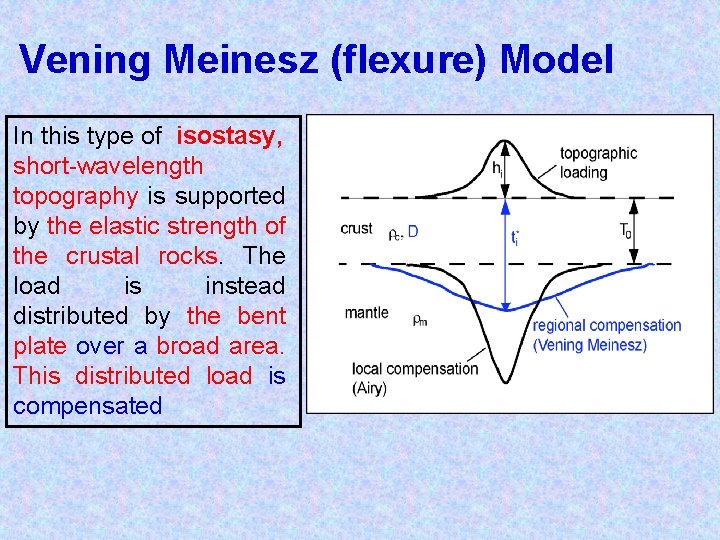
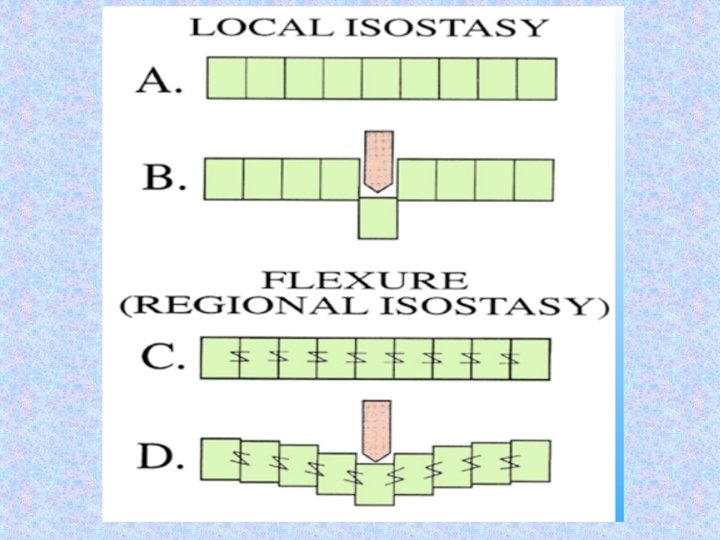
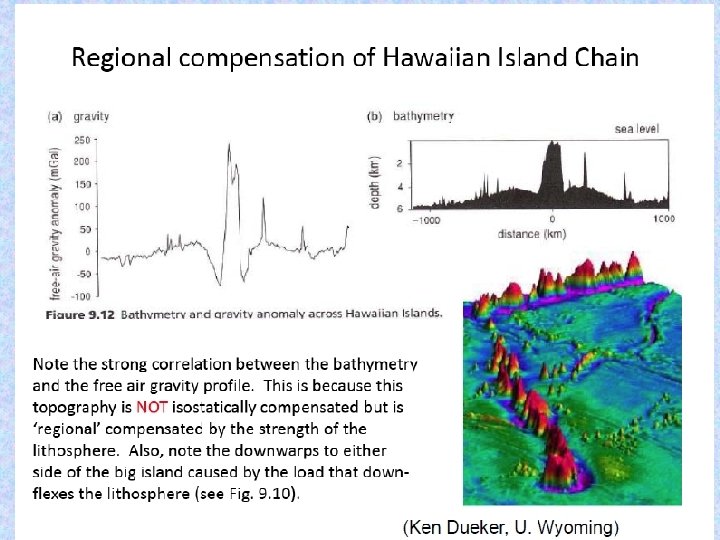
Vening Meinesz (flexure) Model In this type of isostasy, short-wavelength topography is supported by the elastic strength of the crustal rocks. The load is instead distributed by the bent plate over a broad area. This distributed load is compensated

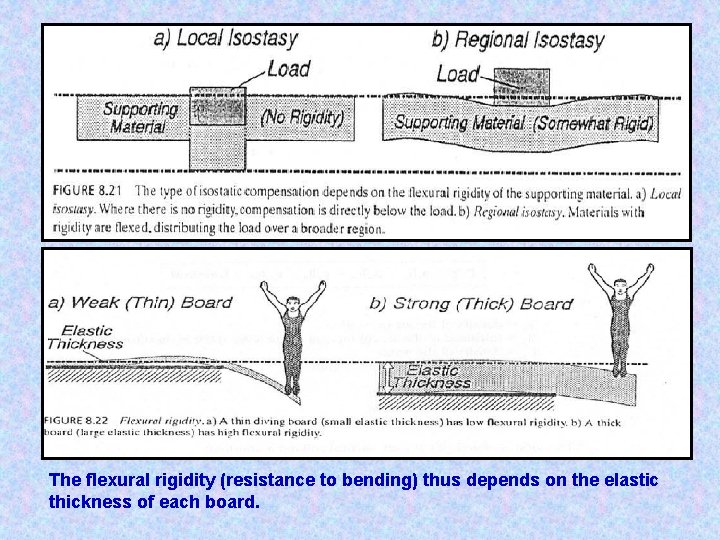
The flexural rigidity (resistance to bending) thus depends on the elastic thickness of each board.

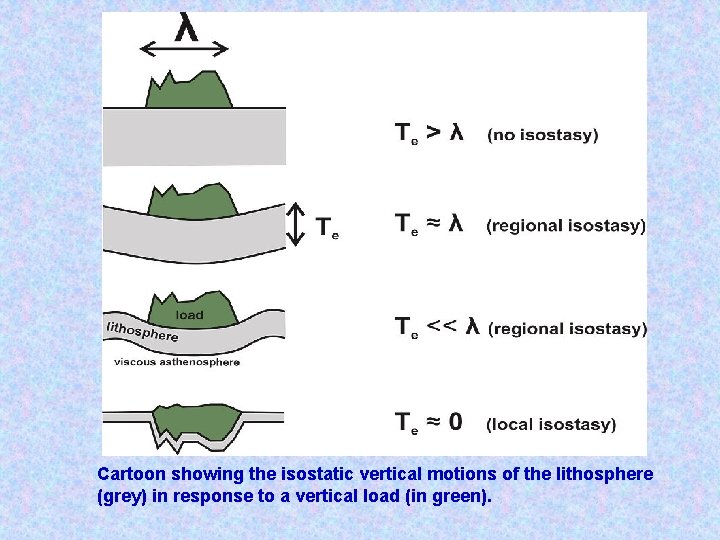
Cartoon showing the isostatic vertical motions of the lithosphere (grey) in response to a vertical load (in green).

Isostatic correction Airy’s isostatic model is preferred geologically and seismologically, whereas Pratt’s model is easier to use to calculate the isostatic correction (e. g. Rimbert et al. , 1987), but the results are similar. Pratt’s model was developed by Heiskanen (1938), who suggested that density changes laterally with variable thickness of crust and that density increases gradually with depth. The aim of the isostatic correction is that effects on g of the large -scale changes in density should be removed, thereby isolating the Bouguer anomaly due to lateral variations in density in the upper crust (Hayford and Bowie, 1912).

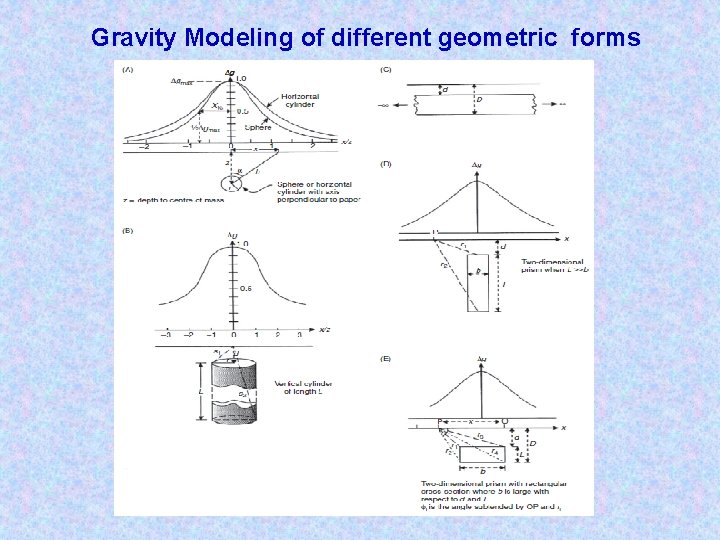
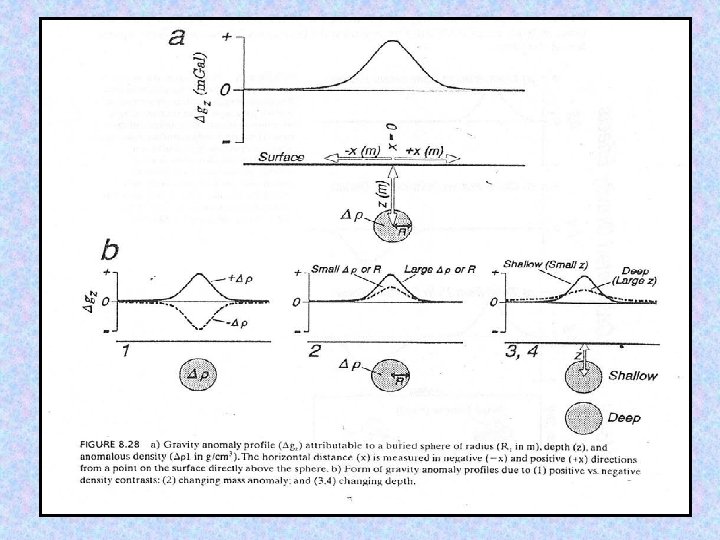
Gravity Modeling of different geometric forms

Gravity anomalies associated with geometric forms

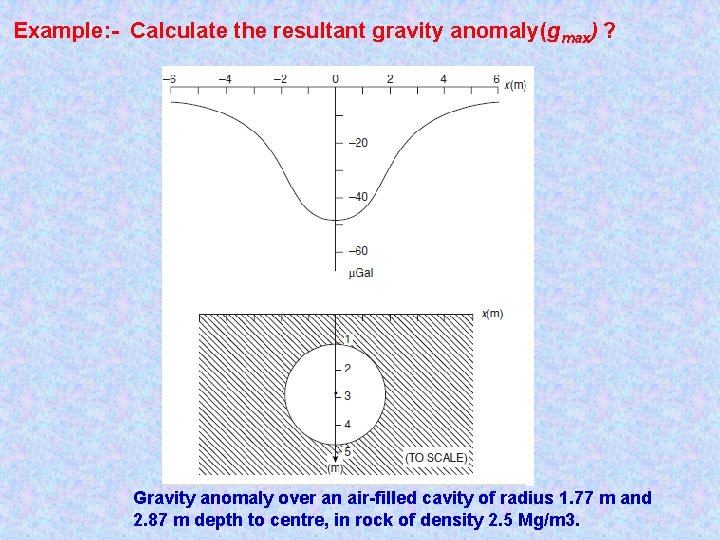
Example: - Calculate the resultant gravity anomaly(gmax) ? Gravity anomaly over an air-filled cavity of radius 1. 77 m and 2. 87 m depth to centre, in rock of density 2. 5 Mg/m 3.