Genetic simplex model in the classical twin design

Genetic simplex model in the classical twin design Conor Dolan & Sanja Franic Boulder Workshop 2016 boulder 2016 dolan & franic simplex model 1

Two general approaches to longitudinal modeling (not mutually exclusive) Markov models: (Vector) autoregressive models for continuous data (Hidden) Markov transition models discrete data Growth curve models: Focus on linear and non-linear growth curves Typically multilevel or random effects model Which to use? Use the model that fit theory / data / hypotheses boulder 2016 dolan & franic simplex model 2

Growth curve modeling ? If you’re interested in growth trajectories. Linear or non-linear: Autoregressive modeling ? If you’re mainly interested in stability. Can be combined (this afternoon) boulder 2016 dolan & franic simplex model 3

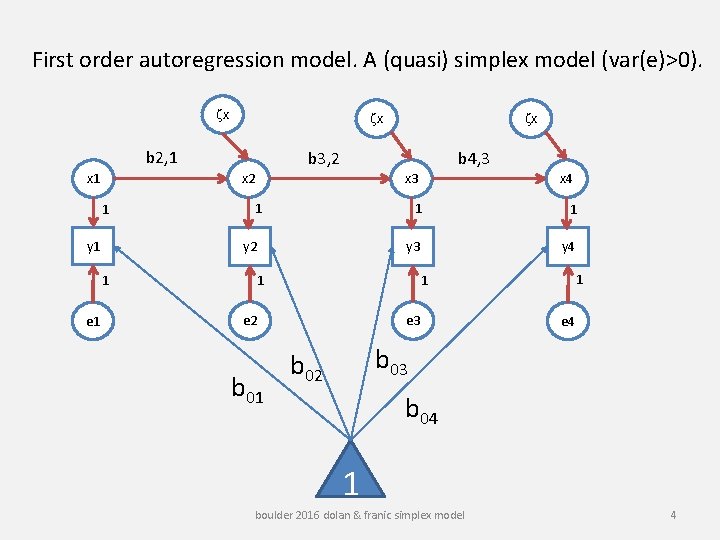
First order autoregression model. A (quasi) simplex model (var(e)>0). zx zx b 2, 1 x 1 y 1 b 4, 3 x 3 1 y 2 1 e 1 b 3, 2 x 2 1 zx 1 1 y 3 y 4 1 1 1 e 2 b 01 x 4 e 3 e 4 b 03 b 02 b 04 1 boulder 2016 dolan & franic simplex model 4

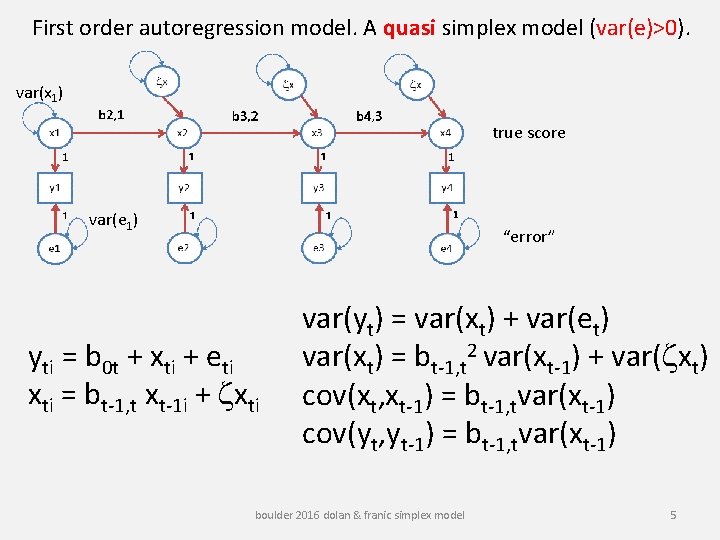
First order autoregression model. A quasi simplex model (var(e)>0). var(x 1) true score var(e 1) “error” yti = b 0 t + xti + eti xti = bt-1, t xt-1 i + zxti var(yt) = var(xt) + var(et) var(xt) = bt-1, t 2 var(xt-1) + var(zxt) cov(xt, xt-1) = bt-1, tvar(xt-1) cov(yt, yt-1) = bt-1, tvar(xt-1) boulder 2016 dolan & franic simplex model 5

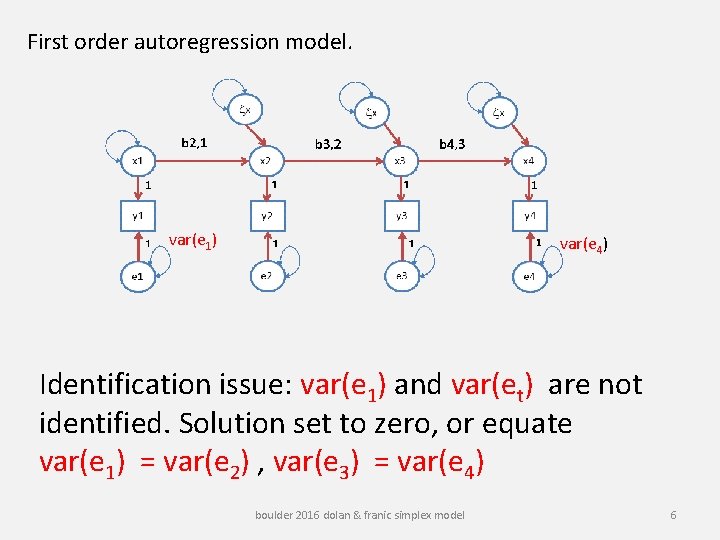
First order autoregression model. var(e 1) var(e 4) Identification issue: var(e 1) and var(et) are not identified. Solution set to zero, or equate var(e 1) = var(e 2) , var(e 3) = var(e 4) boulder 2016 dolan & franic simplex model 6

var(yt) = var(xt) + var(et) var(xt) = bt-1, t 2 var(xt-1) + var(zxt) cov(xt, xt-1) = bt-1, tvar(xt-1) cov(yt, yt-1) = bt-1, tvar(xt-1) Standardized stats part I: “Reliability” at each t, rel(yt) : rel(yt) = var(xt) / {var(xt) + var(et)} Interpretation: % of variance in yt due to latent xt boulder 2016 dolan & franic simplex model 7

var(yt) = var(xt) + var(et) var(xt) = bt-1, t 2 var(xt-1) + var(zxt) cov(xt, xt-1) = bt-1, tvar(xt-1) cov(yt, yt-1) = bt-1, tvar(xt-1) Standardized stats part II: Stability at level of X, stab(Xt, Xt-1): bt-1, t 2 var(xt) / {bt-1, t 2 var(xt-1) + var(zxt)} Interpretation: % of the variance in xt due to xt-1 boulder 2016 dolan & franic simplex model 8

var(yt) = var(xt) + var(et) var(xt) = bt-1, t 2 var(xt-1) + var(zxt) cov(xt, xt-1) = bt-1, tvar(xt-1) cov(yt, yt-1) = bt-1, tvar(xt-1) Standardized stats part III: Correlation t, t-1, cor(t, t-1): bt-1, t var(xt-1) / {sd(yt-1) * sd(yt)} sd(yt) = √(var(xt) + var(et)) var(xt) = bt-1, t var(xt-1) + var(zxt) Interpretation: strength of linear relationship boulder 2016 dolan & franic simplex model 9

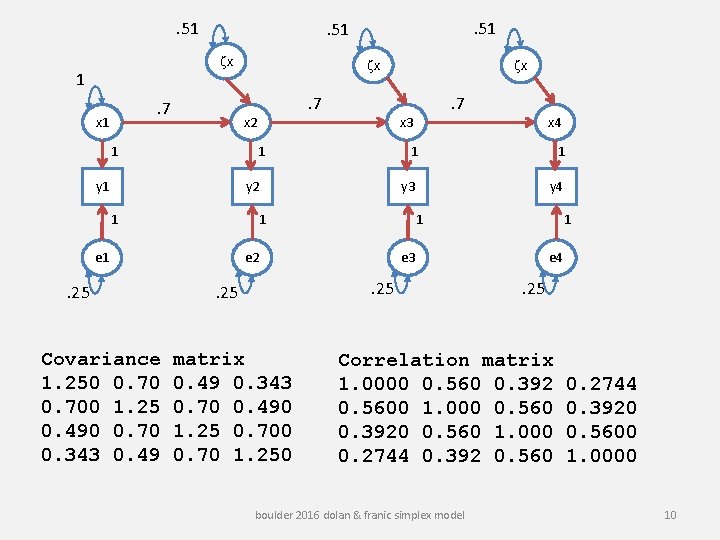
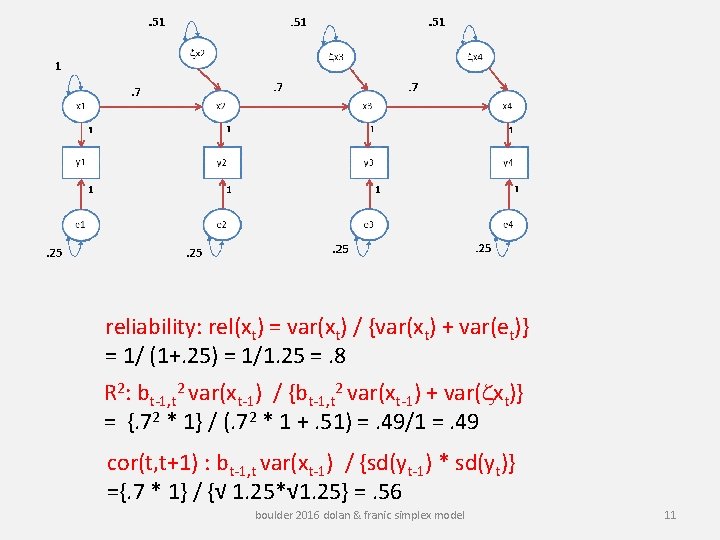
. 51 zx 1. 7 x 1 . 51 zx . 7 x 2 y 1 y 2 1 . 25 Covariance 1. 250 0. 700 1. 25 0. 490 0. 70 0. 343 0. 49 1 y 3 y 4 e 3 . 25 matrix 0. 49 0. 343 0. 70 0. 490 1. 25 0. 700 0. 70 1. 250 1 1 e 2 . 25 x 4 1 1 e 1 . 7 x 3 1 1 zx e 4 . 25 Correlation matrix 1. 0000 0. 560 0. 392 0. 5600 1. 000 0. 560 0. 3920 0. 560 1. 000 0. 2744 0. 392 0. 560 boulder 2016 dolan & franic simplex model 0. 2744 0. 3920 0. 5600 1. 0000 10

reliability: rel(xt) = var(xt) / {var(xt) + var(et)} = 1/ (1+. 25) = 1/1. 25 =. 8 R 2: bt-1, t 2 var(xt-1) / {bt-1, t 2 var(xt-1) + var(zxt)} = {. 72 * 1} / (. 72 * 1 +. 51) =. 49/1 =. 49 cor(t, t+1) : bt-1, t var(xt-1) / {sd(yt-1) * sd(yt)} ={. 7 * 1} / {√ 1. 25*√ 1. 25} =. 56 boulder 2016 dolan & franic simplex model 11

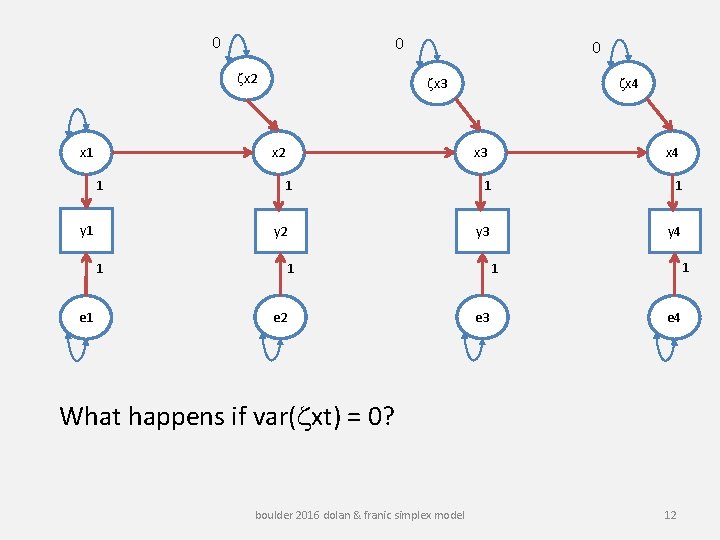
0 0 zx 2 x 1 zx 3 x 2 1 y 1 1 y 2 1 e 1 0 zx 4 x 3 x 4 1 1 y 3 y 4 1 e 2 1 1 e 3 e 4 What happens if var(zxt) = 0? boulder 2016 dolan & franic simplex model 12

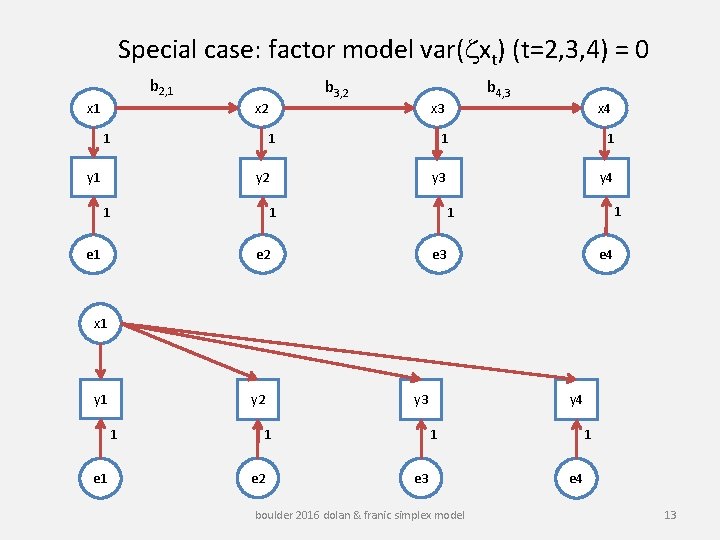
Special case: factor model var(zxt) (t=2, 3, 4) = 0 b 2, 1 x 1 b 3, 2 x 3 1 1 y 2 1 x 4 1 1 y 3 y 4 1 1 1 e 2 e 1 b 4, 3 e 4 x 1 y 2 1 e 1 y 3 1 e 2 y 4 1 1 e 3 boulder 2016 dolan & franic simplex model e 4 13

Multivariate decomposition of phenotypic covariance matrix (Tx. T, say T=4): Sph = SA + SC + SE Sph 12 Sph 2 SA + SC + SE r SA + SC + SE = r SA + SC + SE (r=1 or. 5) boulder 2016 dolan & franic simplex model 14

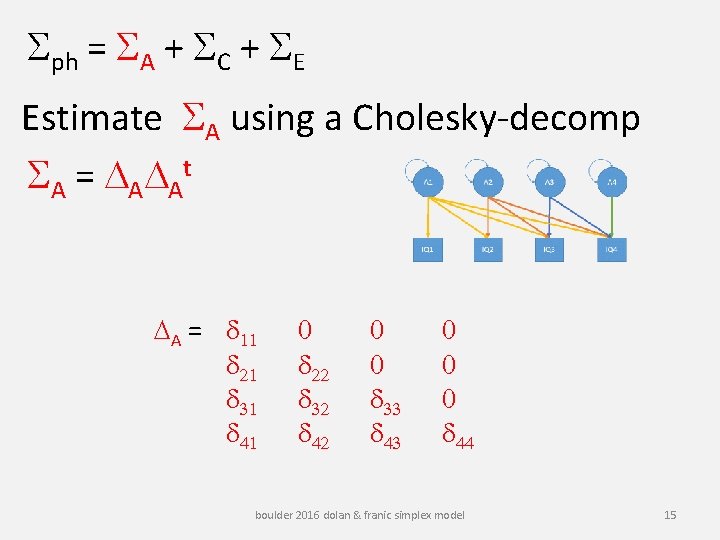
Sph = SA + SC + SE Estimate SA using a Cholesky-decomp S A = D AD At DA = d 11 d 21 d 31 d 41 0 d 22 d 32 d 42 0 0 d 33 d 43 0 0 0 d 44 boulder 2016 dolan & franic simplex model 15

Sph = SA + SC + SE Model SA using a simplex model SA = (I-B)A-1 YA (I-B)A-1 t + QA boulder 2016 dolan & franic simplex model 16

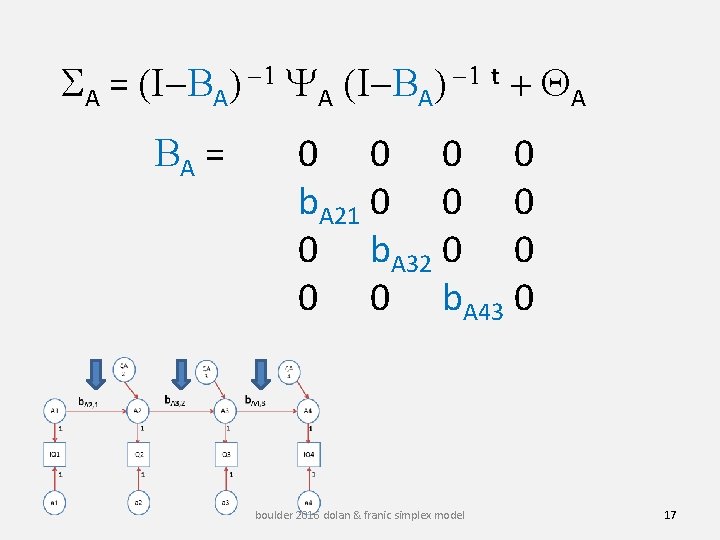
SA = (I-BA) -1 YA (I-BA) -1 t + QA BA = 0 0 b. A 21 0 0 b. A 32 0 0 b. A 43 0 boulder 2016 dolan & franic simplex model 17

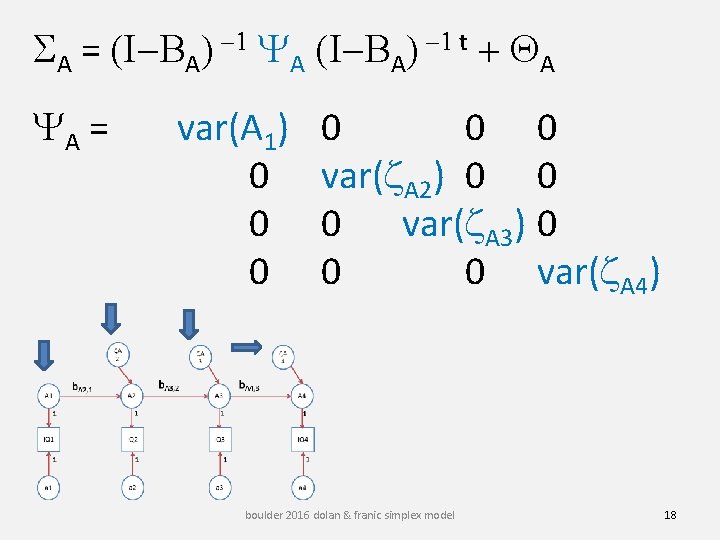
SA = (I-BA) -1 YA (I-BA) -1 t + QA YA = var(A 1) 0 0 0 var(z. A 2) 0 0 0 var(z. A 3) 0 0 0 var(z. A 4) boulder 2016 dolan & franic simplex model 18

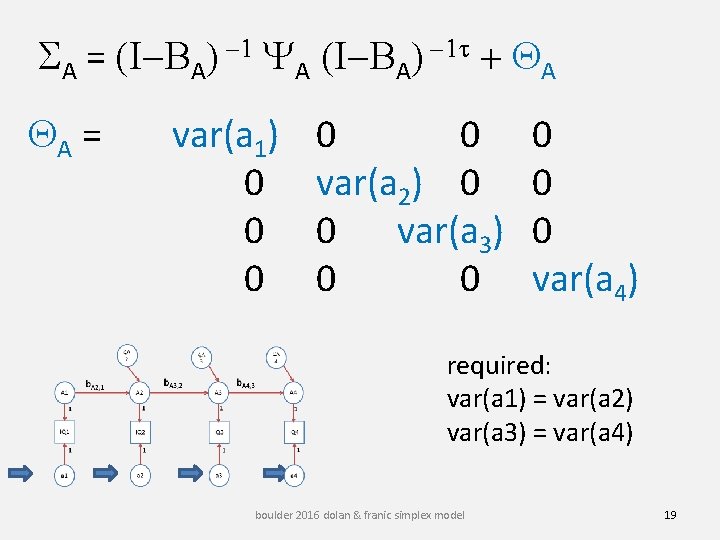
SA = (I-BA) -1 YA (I-BA) -1 t + QA QA = var(a 1) 0 0 0 var(a 2) 0 0 var(a 3) 0 0 0 var(a 4) required: var(a 1) = var(a 2) var(a 3) = var(a 4) boulder 2016 dolan & franic simplex model 19

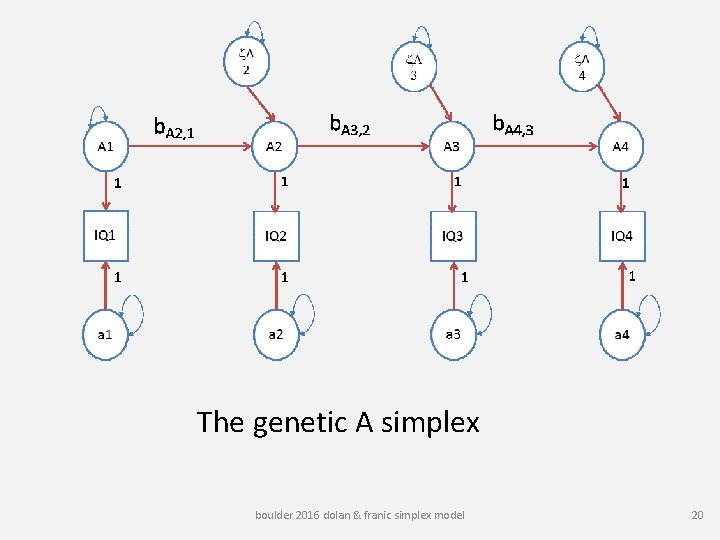
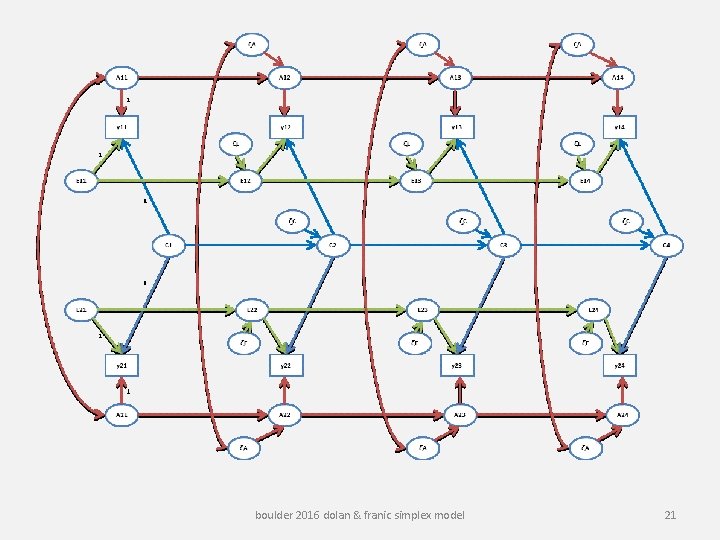
The genetic A simplex boulder 2016 dolan & franic simplex model 20

boulder 2016 dolan & franic simplex model 21

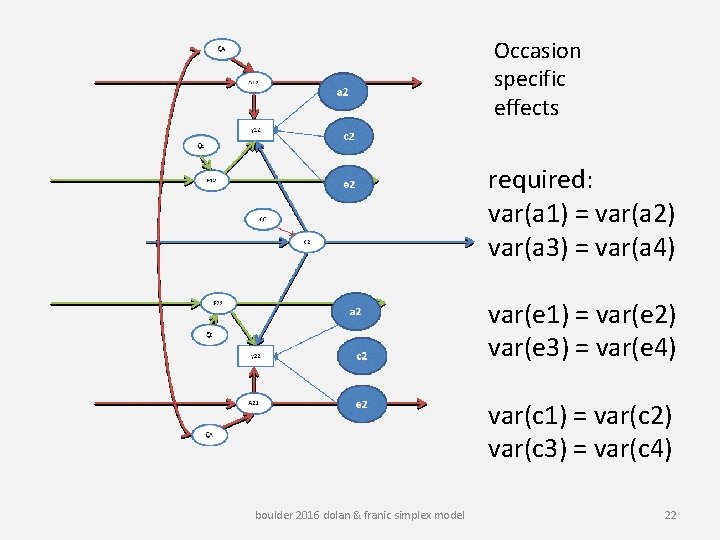
Occasion specific effects required: var(a 1) = var(a 2) var(a 3) = var(a 4) var(e 1) = var(e 2) var(e 3) = var(e 4) var(c 1) = var(c 2) var(c 3) = var(c 4) boulder 2016 dolan & franic simplex model 22

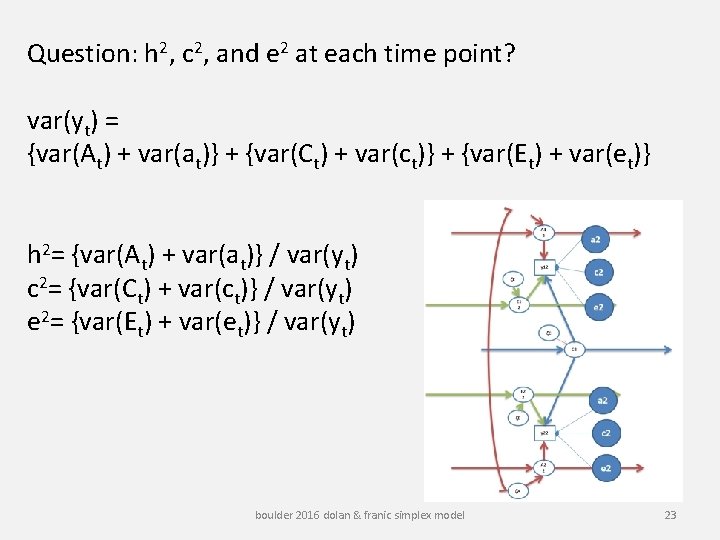
Question: h 2, c 2, and e 2 at each time point? var(yt) = {var(At) + var(at)} + {var(Ct) + var(ct)} + {var(Et) + var(et)} h 2= {var(At) + var(at)} / var(yt) c 2= {var(Ct) + var(ct)} / var(yt) e 2= {var(Et) + var(et)} / var(yt) boulder 2016 dolan & franic simplex model 23

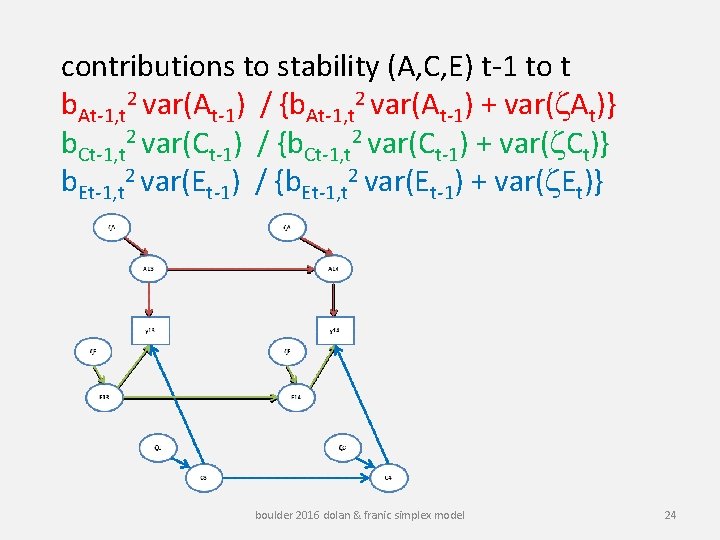
contributions to stability (A, C, E) t-1 to t b. At-1, t 2 var(At-1) / {b. At-1, t 2 var(At-1) + var(z. At)} b. Ct-1, t 2 var(Ct-1) / {b. Ct-1, t 2 var(Ct-1) + var(z. Ct)} b. Et-1, t 2 var(Et-1) / {b. Et-1, t 2 var(Et-1) + var(z. Et)} boulder 2016 dolan & franic simplex model 24

contributions of A to Phenotypic stability t-1 to t b. At-1, t 2 var(At-1) {b. At-1, t 2 var(At-1) + var(z. At)} + {b. Ct-1, t 2 var(Ct-1) + var(z. Ct)} + {b. Et-1, t 2 var(Et-1) + var(z. Et)} boulder 2016 dolan & franic simplex model 25

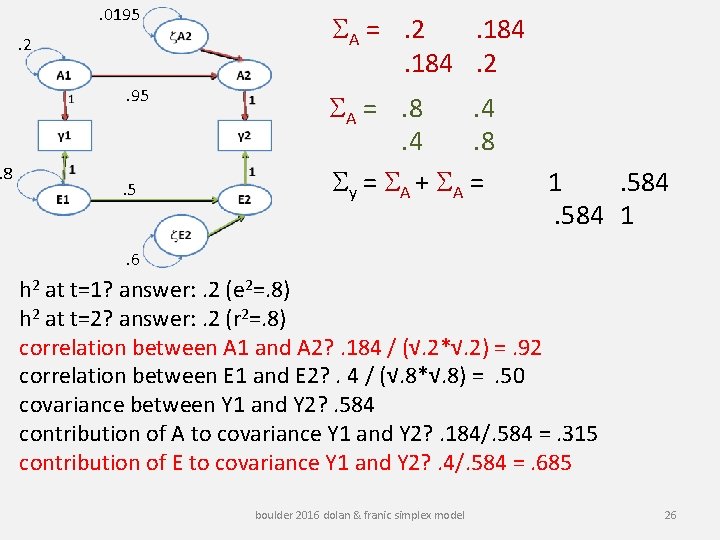
. 8 . 0195. 2. 95 . 5 SA =. 2. 184. 2 SA =. 8. 4. 4. 8 Sy = SA + SA = 1. 584 1 . 6 h 2 at t=1? answer: . 2 (e 2=. 8) h 2 at t=2? answer: . 2 (r 2=. 8) correlation between A 1 and A 2? . 184 / (√. 2*√. 2) =. 92 correlation between E 1 and E 2? . 4 / (√. 8*√. 8) =. 50 covariance between Y 1 and Y 2? . 584 contribution of A to covariance Y 1 and Y 2? . 184/. 584 =. 315 contribution of E to covariance Y 1 and Y 2? . 4/. 584 =. 685 boulder 2016 dolan & franic simplex model 26

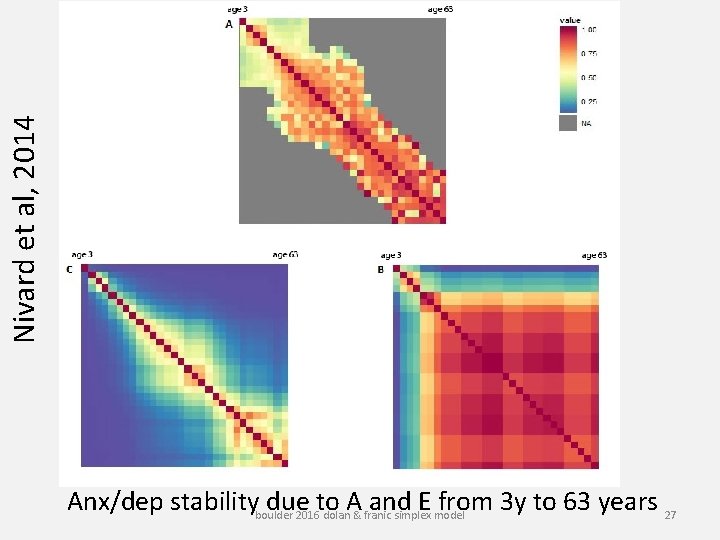
Nivard et al, 2014 Anx/dep stabilityboulder due 2016 to A and E from 3 y to 63 years 27 dolan & franic simplex model

Sanja’s Practical: the genetic simplex model applied to FSIQ at 4 occasions. But first. . Variations on theme boulder 2016 dolan & franic simplex model 28

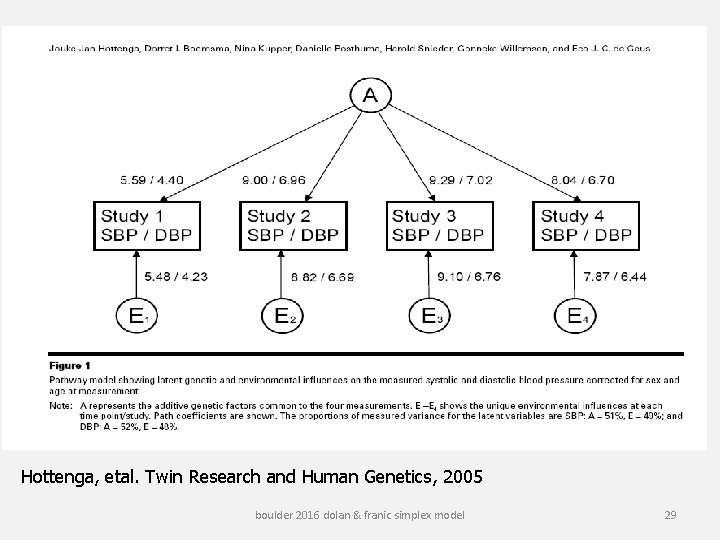
Hottenga, etal. Twin Research and Human Genetics, 2005 boulder 2016 dolan & franic simplex model 29

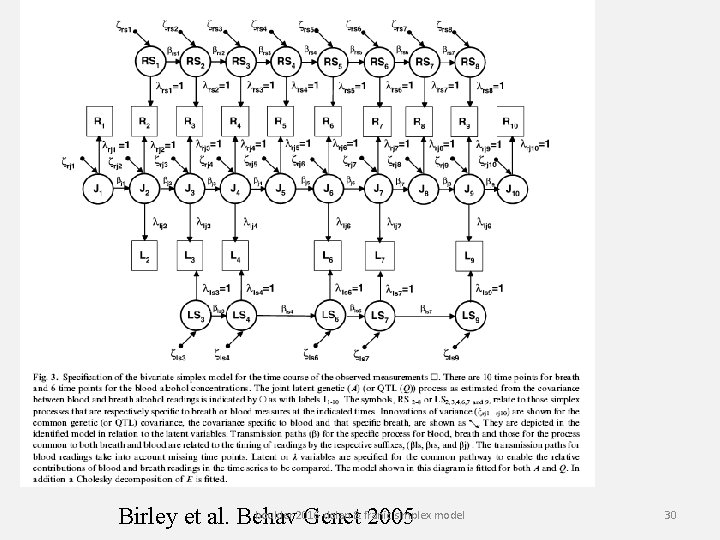
boulder 2016 dolan & franic simplex model Birley et al. Behav Genet 2005 30

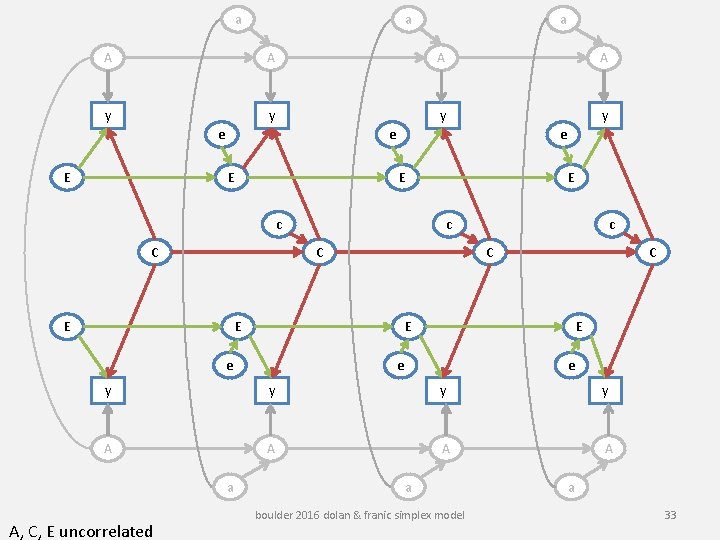
“Niche-picking” During development children seek out and create and are furnished surrounding (E) that fit their phenotype. A smart child growing up will pick the niche that fits her/her phenotypic intelligence. A anxious child growing up may pick out the niche that least aggrevates his / her phenotypic anxiety. Phenotype of twin 1 at time t -> environment of twin 1 at time t+1 boulder 2016 dolan & franic simplex model 31

Mutual influences During development children’s behavior may contribute to the environment of their siblings. A smart child growing up will pick the niche that fits her/her phenotypic intelligence and in so doing may influence (contriibute to) the environment of his or her sibling. A behavior of an anxious child may be a source of stress for his or her siblings. Phenotype of twin 1 at time t -> environment of twin 2 at time t+1 boulder 2016 dolan & franic simplex model 32

a a a A A y y e E e E E c C E e E e e y y A A a A, C, E uncorrelated a boulder 2016 dolan & franic simplex model a 33

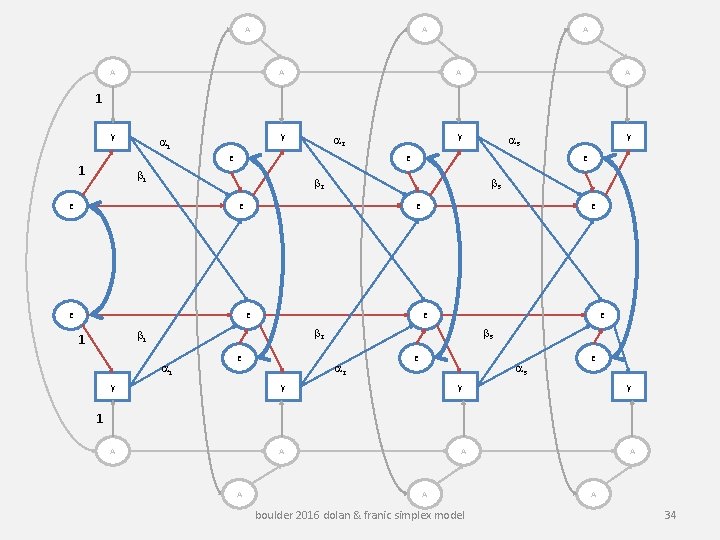
A A A A 1 y y a 1 E 1 y a 2 E b 1 E b 2 E b 3 E E E E b 2 b 1 1 a 1 y a 3 E b 3 a 2 E a 3 E y y A A 1 A A boulder 2016 dolan & franic simplex model A 34

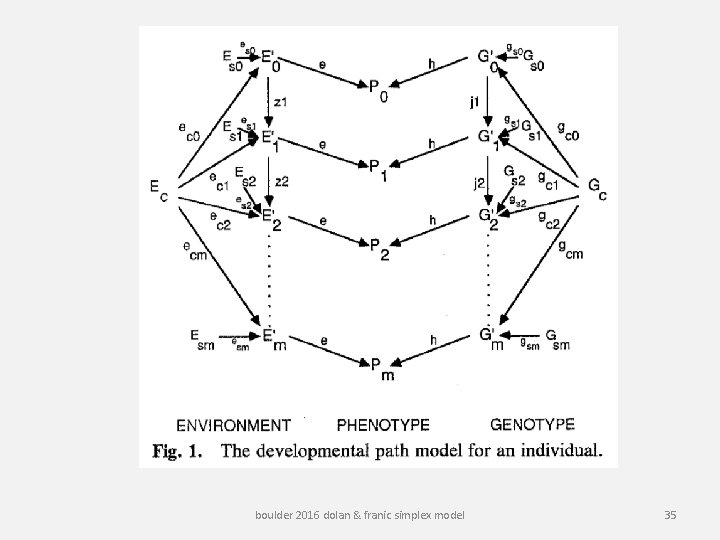
boulder 2016 dolan & franic simplex model 35

Environments selected by genotypes (Scarr & Mc. Cartny, 1983; Plomin, De. Fries & Loehlin, 1977) Sibling effects (Carey, 1986, Behav Genet 16: 319– 341) boulder 2016 dolan & franic simplex model 36

boulder 2016 dolan & franic simplex model 37

boulder 2016 dolan & franic simplex model 38

boulder 2016 dolan & franic simplex model 39

boulder 2016 dolan & franic simplex model 40

Mi - chael boulder 2016 dolan & franic simplex model 41