Genetic Polymorphism and Speciation An Adaptive Dynamics Perspective

Genetic Polymorphism and Speciation - An Adaptive Dynamics Perspective - Eva Kisdi & Stefan Geritz Dept. of Mathematics, University of Turku

Evolutionary branching http: //users. utu. fi/evakis/addyn. htm

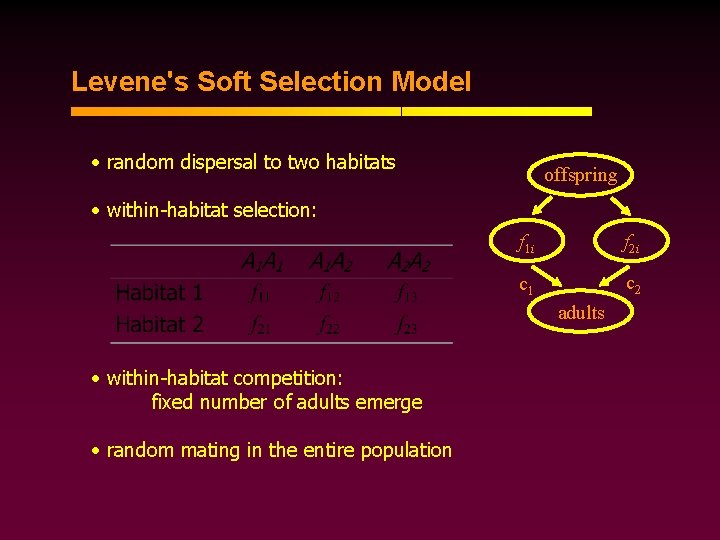
Levene's Soft Selection Model • random dispersal to two habitats offspring • within-habitat selection: f 1 i f 2 i c 1 c 2 adults • within-habitat competition: fixed number of adults emerge • random mating in the entire population

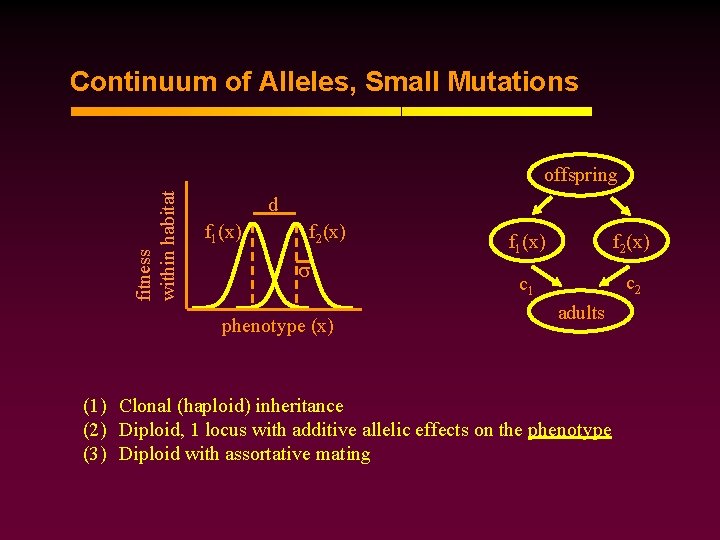
Continuum of Alleles, Small Mutations fitness within habitat offspring d f 1(x) f 2(x) phenotype (x) f 1(x) f 2(x) c 1 c 2 adults (1) Clonal (haploid) inheritance (2) Diploid, 1 locus with additive allelic effects on the phenotype (3) Diploid with assortative mating

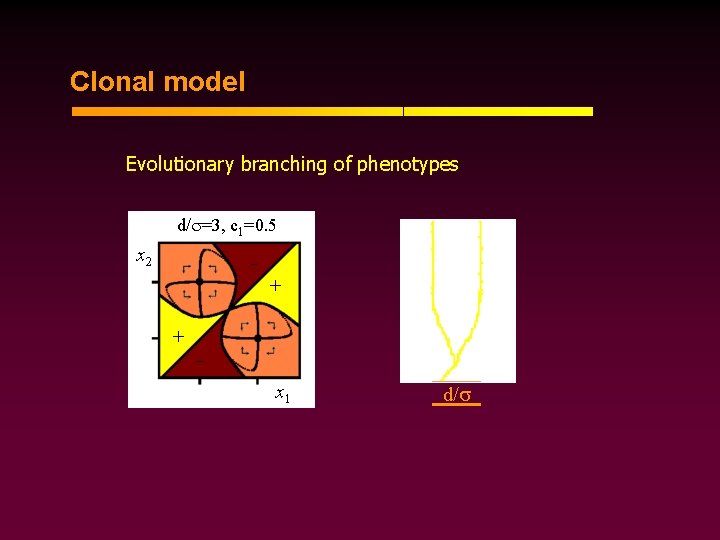
Clonal model Evolutionary branching of phenotypes d/ =3, c 1=0. 5 x 2 + + x 1 d/

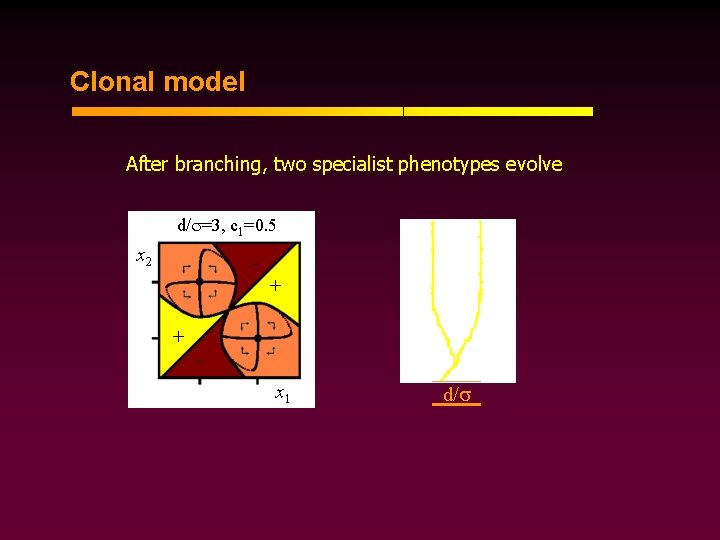
Clonal & diploid models Clonal model: evolutionary branching of phenotypes Diploid 1 -locus model: evolutionary branching of alleles c 1 (d/ )2 > 1/c 1 c 2 d/ Infinite loci, +/- alleles: Genetic polymorphism in each locus (Spichtig & Kawecki, in press) Two loci, continuum of alleles: Initially both loci undergo branching, but only one remains polymorphic (Kisdi & Geritz 1999)

Genetic Polymorphism Protected polymorphism of similar alleles – under weak selection - ? ! Evolving alleles: Fixed alleles: + + - Hoekstra et al. 1985

Genetic Polymorphism Generic models of a wide class, both clonal and diploid: no polymorphism of similar alleles away from singularities invasion implies fixation near a singularity, protected polymorphism or rare disadvantage of similar alleles fine-tuning done by directional evolution if the singularity is an ESS, then the polymorphism is transient on the long-term evolutionary timescale not every polymorphism is evolutionarily permanent

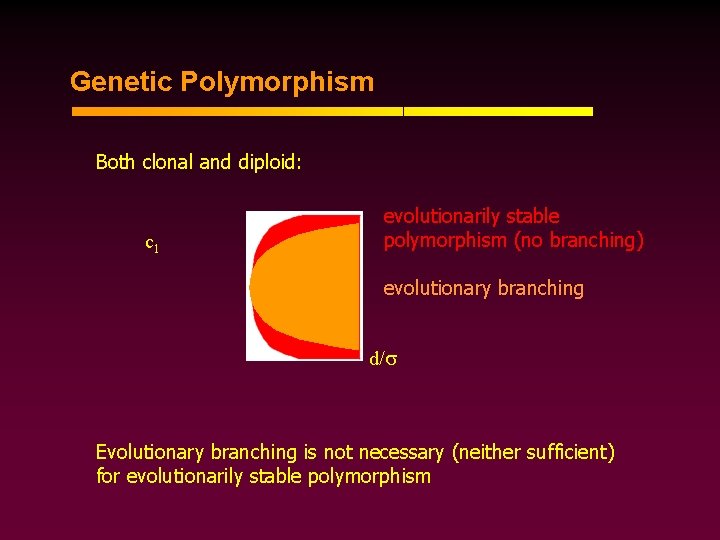
Genetic Polymorphism Both clonal and diploid: c 1 evolutionarily stable polymorphism (no branching) evolutionary branching d/ Evolutionary branching is not necessary (neither sufficient) for evolutionarily stable polymorphism

Clonal model After branching, two specialist phenotypes evolve d/ =3, c 1=0. 5 x 2 + + x 1 d/

Diploid model d/ =2. 25, c 1=0. 5 d/ =3, c 1=0. 5 d/ =5, c 1=0. 5 x 2 x 1 x 1 Will assortative mating restore the simplicity of the clonal model?

Assortative mating "Two-allele mechanisms": (Felsenstein, 1981) strong selection is necessary to counterbalance recombination Evolution to strongest heterozygote inferiority Time window for speciation

Population Genetics of Assortative mating Udovic (1980) model: mating locus with two alleles (B, b) mating groups: BB+Bb and bb p = penetrance: mating within group with prob. p, otherwise random mating r = recombination between the ecological and the mating locus In linkage equilibrium, alleles B and b are neutral

Population Genetics of Assortative Mating Ecological locus (no mutation): Mating locus: B, b u = freq(x 1) = 0. 5 v = freq(b) Gamete frequencies: in the dominant (BB+Bb) mating group in the recessive (bb) mating group overall Zygote frequencies: except

Population Genetics of Assortative Mating Zygote frequencies: except Selection by the ecological locus: relative fitnesses Gamete frequencies by the standard Mendelian rules within each mating group recombination rate r 6 variables – 1 (sum of the Q's is 1) – 1 (symmetry, u=0. 5)

Population Genetics of Assortative Mating p = 0. 75 r = 0. 5 s = 0. 358 (max s with d/s=3, c 1=0. 5) v=freq(b) vcrit D = qib - uv Bistability of the gamete frequency dynamics: LE is stable LE is unstable

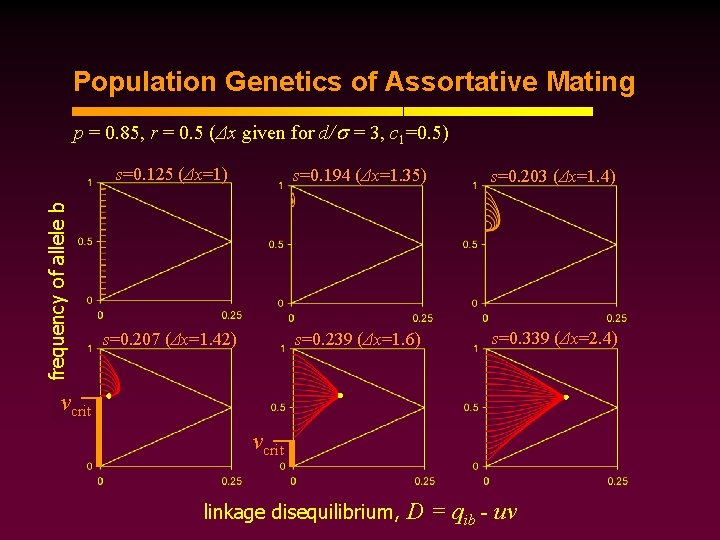
Population Genetics of Assortative Mating frequency of allele b p = 0. 85, r = 0. 5 (Δx given for d/s = 3, c 1=0. 5) s=0. 125 (Δx=1) s=0. 194 (Δx=1. 35) s=0. 203 (Δx=1. 4) s=0. 207 (Δx=1. 42) s=0. 239 (Δx=1. 6) s=0. 339 (Δx=2. 4) vcrit linkage disequilibrium, D = qib - uv

recombination (r) Population Genetics of Assortative Mating penetrance (p) LD evolves if v is high enough 1 LD does not evolve s = 0. 358 (maximum for d/s=3, c 1=0. 5)

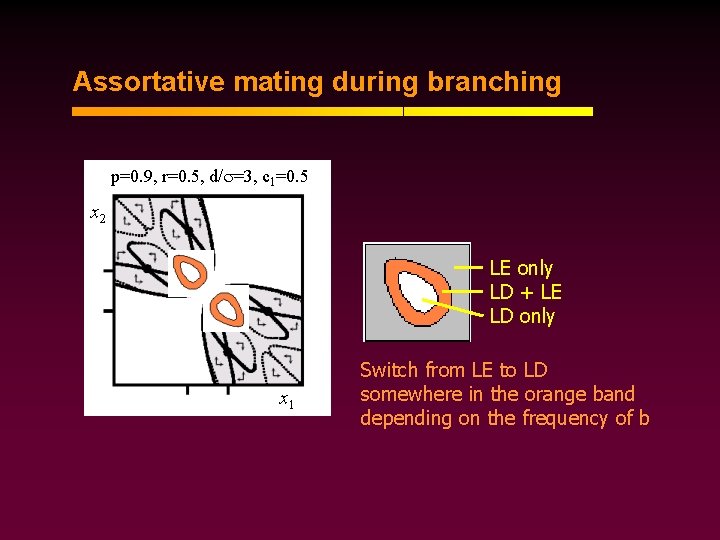
Assortative mating during branching p=0. 9, r=0. 5, d/ =3, c 1=0. 5 x 2 LE only LD + LE LD only x 1 Switch from LE to LD somewhere in the orange band depending on the frequency of b

Adaptive dynamics of alleles at LD p=0. 9, r=0. 5, d/ =3, c 1=0. 5 x 2 x 1 d/ F heterozygote deficiency before / after selection

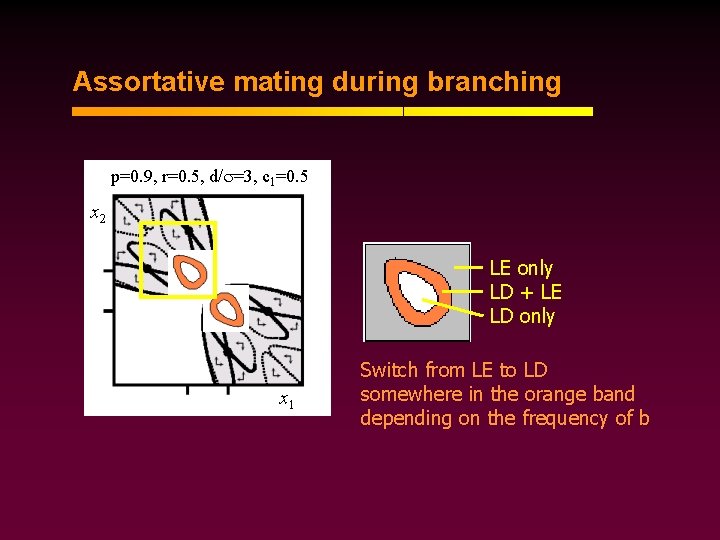
Assortative mating during branching p=0. 9, r=0. 5, d/ =3, c 1=0. 5 x 2 LE only LD + LE LD only x 1 Switch from LE to LD somewhere in the orange band depending on the frequency of b

Adaptive dynamics of alleles at LD LD permanent – incipient speciation LD lost p=0. 73, r=0. 5, d/ =3, c 1=0. 5 p=0. 85, r=0. 5, d/ =3, c 1=0. 5 x 2 x 1 LD exists LE only x 1

Prospects for speciation recombination (r) Levene model with d/s = 3, c 1 = 0. 5 penetrance (p) Left to the red line: AD saddle LD may evolve but will be lost 1 LD does not evolve Right to the red line: AD attractor LD evolves if v is high enough

Prospects for speciation B and b are neutral at LE - mutational equilibrium - drift and hitchhiking: the frequency of allele b, v, is most often near 0 (LD in ) or near 1 (LD in and ) - sexual selection: if rare males are at a disadvantage, B or b will be rare and selected against Increasing penetrance - natural selection favours increased p at LD - increasing p transforms a saddle into an attractor of AD - closes gene flow down - role of temporary LD in increasing penetrance (Dieckmann and Doebeli 1999)

Prospects for speciation "Byproduct" speciation - no LD is needed between the ecological and mating loci - sexual selection may counterbalance disruptive natural selection (Kirkpatrick and Nuismer 2004), and causes a bistability in the evolutionary dynamics of assortment (Matessi et al. 2001, Meszéna and Christiansen in prep. ) - environmental variance in the selected trait constrains the maximum attainable level of assortment

An Adaptive Dynamics Perspective. . . on polymorphism directional evolution takes care of "fine tuning" polymorphism may be transient in evolution (evolution near an ESS, evolution to extinction) evolutionary branching is neither necessary nor sufficient for an evolutionarily stable polymorphism to exist. . . on speciation evolution can lead to strong disruptive selection but can lead away from it again (time window) competing processes: evolution of dominance, sexual dimorphism, mixed strategies

An Adaptive Dynamics Perspective. . . on speciation - evolution to polymorphism under disruptive selection appears to be common - reproductive isolation: depends on genetics Alliance with population genetics needed!