Genetic Algorithms Introduction To Genetic Algorithms GAs 3

Genetic Algorithms

Introduction To Genetic Algorithms (GAs) 3

What Are Genetic Algorithms (GAs)? Genetic Algorithms are search and optimization techniques based on Darwin’s Principle of Natural Selection. 4

How is it different from other optimization and search procedures? 1. 2. 3. 4. Works with a coding of the parameter set, not the parameters themselves Search for a population of point and not a single point Use objective function information and not derivatives or other auxiliary knowledge Uses probabilistic transition rules and not deterministic rules

How GA is used and different from other optimization techniques? n n The first step in GA is to code the parameter x as a finite length string Example 1 can be code as string of 5 bits with an output f=f(s) , where s=string of bits Successive populations are generated using the GA For effective check GA requires only objective functions associated with individual strings

Simple genetic algorithm n n n Reproduction: - individual strings are copied according to their objective fn: values f(FITNESS FUNCTION) Crossover: - Members of the newly reproduced strings are mated at random. Each pair of strings undergoes crossing overs. Mutation: -supplements reproduction and crossover and acts as an insurance policy against premature loss of important notions

Darwin’s Principle Of Natural Selection n n n I IF there are organisms that reproduce, and IF offsprings inherit traits from their parents, and IF there is variability of traits, and IF the environment cannot support all members of a growing population, THEN those members of the population with lessadaptive traits (determined by the environment) will die out, and THEN those members with more-adaptive traits (determined by the environment) will thrive The result is the evolution of species. 8

Basic Idea Of Principle Of Natural Selection “Select The Best, Discard The Rest” 9

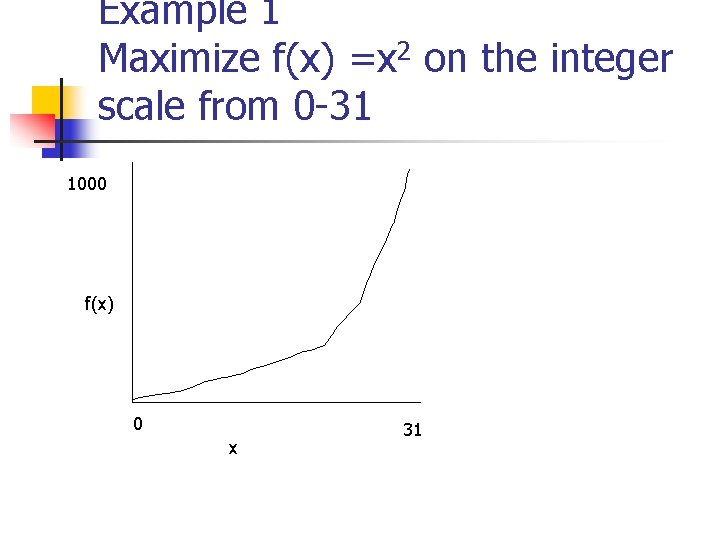
Example 1 Maximize f(x) =x 2 on the integer scale from 0 -31 1000 f(x) 0 x 31

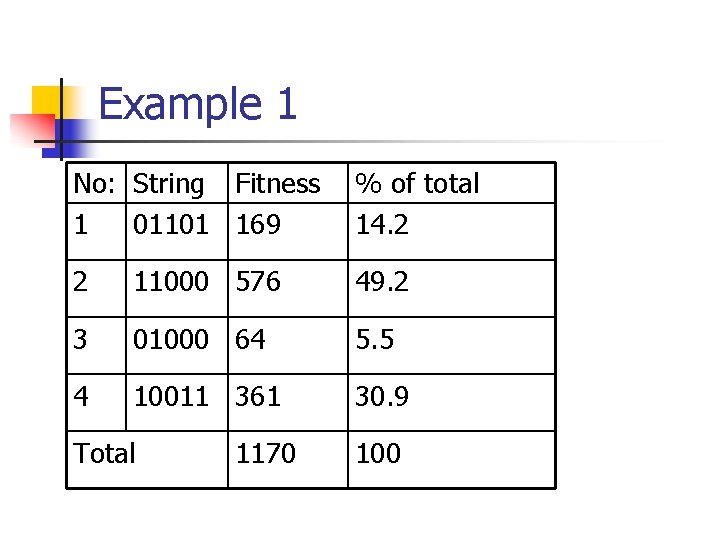
Example 1 No: String Fitness 1 01101 169 % of total 14. 2 2 11000 576 49. 2 3 01000 64 5. 5 4 10011 361 30. 9 Total 1170 100

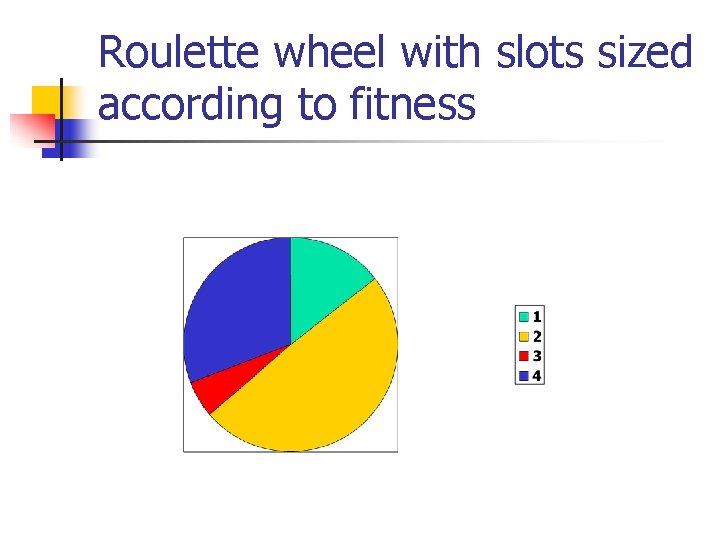
Roulette wheel with slots sized according to fitness

Crossover A 1=0 1 1 0 1 A 2=1 1 0 0 0 A 1’=0 1 1 0 0 A 2’=1 1 0 0 1

Simple GA by Hand(Reproduction) No: String x f(x) x 2 pselect fi/Ʃf Expected count n. pselect Actual count (Roulette Wheel 0 1 01101 13 169 . 14 . 58 1 2 11000 24 576 . 49 1. 97 2 3 01000 08 64 . 06 0. 24 0 4 10011 19 361 0. 31 1. 24 1 Sum 1170 1. 00 4 4. 0 Average 293 0. 25 1. 00 1. 0 Maximum 576 . 49 1. 97 2

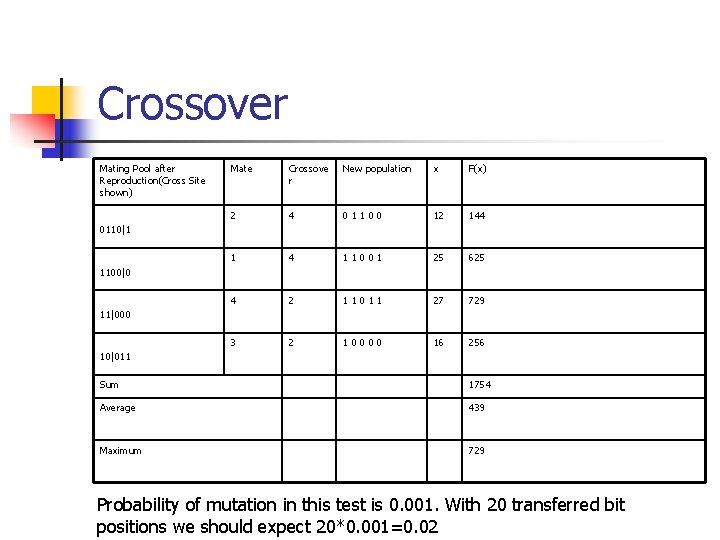
Crossover Mating Pool after Reproduction(Cross Site shown) Mate Crossove r New population x F(x) 2 4 01100 12 144 1 4 11001 25 625 4 2 11011 27 729 3 2 10000 16 256 0110|1 1100|0 11|000 10|011 Sum 1754 Average 439 Maximum 729 Probability of mutation in this test is 0. 001. With 20 transferred bit positions we should expect 20*0. 001=0. 02

How does the directed search guide for improvement? n n Seeking similarities among strings in population Causal relationships between similarities and high fitness

Evolution in the real world n n n n Each cell of a living thing contains chromosomes - strings of DNA Each chromosome contains a set of genes - blocks of DNA Each gene determines some aspect of the organism (like eye colour) A collection of genes is sometimes called a genotype A collection of aspects (like eye colour) is sometimes called a phenotype Reproduction involves recombination of genes from parents and then small amounts of mutation (errors) in copying The fitness of an organism is how much it can reproduce before it dies Evolution based on “survival of the fittest” 17

Basic Idea Of Principle Of Natural Selection “Select The Best, Discard The Rest”

Algorithm Generate Initial Population do Calculate the Fitness of each member do { Select Parents from current population Perform Crossover add offspring to the new population Merge new population into the current population Mutate current population till result is obtained

Population population Chromosomes could be: n n n Bit strings 1100) Real numbers 89. 2) Permutations of element Lists of rules R 23). . . any data structure. . . (0101. . . (43. 2 -33. 1. . . 0. 0 (E 11 E 3 E 7. . . E 15) (R 1 R 2 R 3. . . R 22

Algorithm Generate Initial Population do Calculate the Fitness of each member do { Select Parents from current population Perform Crossover add offspring to the new population Merge new population into the current population Mutate current population till result is obtained

Algorithm Generate Initial Population do Calculate the Fitness of each member do { Select Parents from current population Perform Crossover add offspring to the new population Merge new population into the current population Mutate current population till result is obtained

Fitness Function A fitness function quantifies the optimality of a solution so that particular solution may be ranked against all the other solutions. n n A fitness value is assigned to each solution depending on how close it actually is to solving the problem. Ideal fitness function correlates closely to goal + quickly computable.

Algorithm Generate Initial Population do Calculate the Fitness of each member do { Select Parents from current population Perform Crossover add offspring to the new population Merge new population into the current population Mutate current population till result is obtained

Algorithm Generate Initial Population do Calculate the Fitness of each member do { Select Parents from current population Perform Crossover add offspring to the new population Merge new population into the current population Mutate current population till result is obtained

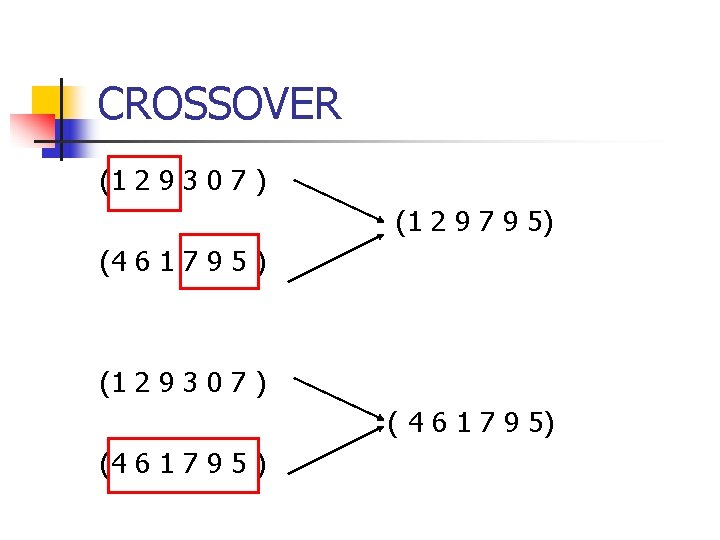
Crossover n Mimics biological recombination n n Some portion of genetic material is swapped between chromosomes Typically the swapping produces an offspring

CROSSOVER (1 2 9 3 0 7 ) (1 2 9 7 9 5) (4 6 1 7 9 5 ) (1 2 9 3 0 7 ) ( 4 6 1 7 9 5) (4 6 1 7 9 5 )

Algorithm Generate Initial Population do Calculate the Fitness of each member do { Select Parents from current population Perform Crossover add offspring to the new population Merge new population into the current population Mutate current population till result is obtained

Algorithm Generate Initial Population do Calculate the Fitness of each member do { Select Parents from current population Perform Crossover add offspring to the new population Merge new population into the current population Mutate current population till result is obtained

Mutation n n Selects a random locus – gene location – with some probability and alters the allele at that locus The intuitive mechanism for the preservation of variety in the population

Mutation: Local Modification Before: After: (1 0 1 1 0) (0 1 1 0) Before: After: (1. 38 -69. 4 326. 44 0. 1) (1. 38 -67. 5 326. 44 0. 1)

The Problem The Traveling Salesman Problem is defined as: Given: 1) A set of cities 2) Symmetric distance matrix that indicates the cost of travel from each city to every other city. Goal: 1) Find the shortest circular tour, visiting every city exactly once. 2) Minimize the total travel cost, which includes the cost of traveling from the last city back to the first city’.

Traveling Salesperson Problem

Encoding n n Represent every city with an integer. Consider 6 Indian cities – Mumbai, Nagpur , Calcutta, Delhi, Bangalore and Pune assign a number to each. Mumbai Nagpur Calcutta Delhi Bangalore Pune 1 2 3 4 5 6 34

Encoding n n Thus a path would be represented as a sequence of integers from 1 to 6. The path [1 2 3 4 5 6] represents a path from Mumbai to Nagpur - Nagpur to Calcutta - Calcutta to Delhi - Delhi to Bangalore - Bangalore to Pune and pune to Mumbai. 35

Fitness Function n n The fitness function will be the total cost of the tour represented by each chromosome. This can be calculated as the sum of the distances traversed in each travel segment. The Lesser The Sum, The Fitter The Solution Represented By That Chromosome.

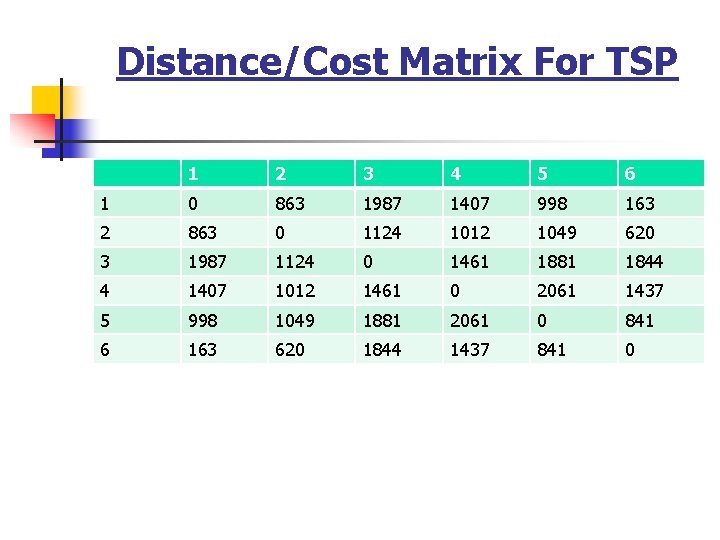
Distance/Cost Matrix For TSP 1 2 3 4 5 6 1 0 863 1987 1407 998 163 2 863 0 1124 1012 1049 620 3 1987 1124 0 1461 1881 1844 4 1407 1012 1461 0 2061 1437 5 998 1049 1881 2061 0 841 6 163 620 1844 1437 841 0

Fitness Function (contd. ) n n n So, for a chromosome [4 1 3 2 5 6 ], the total cost of travel or fitness will be calculated as shown below Fitness = 1407 + 1987 + 1124 + 1049 + 841 = 6408 kms. Since our objective is to Minimize the distance, the lesser the total distance, the fitter the solution.

Initial Population for TSP (5, 3, 4, 6, 2) (2, 4, 6, 3, 5) (4, 3, 6, 5, 2) (2, 3, 4, 6, 5) (4, 3, 6, 2, 5) (3, 4, 5, 2, 6) (3, 5, 4, 6, 2) (4, 5, 3, 6, 2) (5, 4, 2, 3, 6) (4, 6, 3, 2, 5) (3, 4, 2, 6, 5) (3, 6, 5, 1, 4)

Select Parents (5, 3, 4, 6, 2) (2, 4, 6, 3, 5) (4, 3, 6, 5, 2) (2, 3, 4, 6, 5) (4, 3, 6, 2, 5) (3, 4, 5, 2, 6) (3, 5, 4, 6, 2) (4, 5, 3, 6, 2) (5, 4, 2, 3, 6) (4, 6, 3, 2, 5) (3, 4, 2, 6, 5) (3, 6, 5, 1, 4) Try to pick the better ones.

Create Off-Spring – 1 point (5, 3, 4, 6, 2) (2, 4, 6, 3, 5) (4, 3, 6, 5, 2) (2, 3, 4, 6, 5) (4, 3, 6, 2, 5) (3, 4, 5, 2, 6) (3, 5, 4, 6, 2) (4, 5, 3, 6, 2) (5, 4, 2, 3, 6) (4, 6, 3, 2, 5) (3, 4, 2, 6, 5) (3, 6, 5, 1, 4) (3, 4, 5, 6, 2)

Create More Offspring (5, 3, 4, 6, 2) (2, 4, 6, 3, 5) (4, 3, 6, 5, 2) (2, 3, 4, 6, 5) (4, 3, 6, 2, 5) (3, 4, 5, 2, 6) (3, 5, 4, 6, 2) (4, 5, 3, 6, 2) (5, 4, 2, 3, 6) (4, 6, 3, 2, 5) (3, 4, 2, 6, 5) (3, 6, 5, 1, 4) (3, 4, 5, 6, 2) (5, 4, 2, 6, 3)

Mutate (5, 3, 4, 6, 2) (2, 4, 6, 3, 5) (4, 3, 6, 5, 2) (2, 3, 4, 6, 5) (4, 3, 6, 2, 5) (3, 4, 5, 2, 6) (3, 5, 4, 6, 2) (4, 5, 3, 6, 2) (5, 4, 2, 3, 6) (4, 6, 3, 2, 5) (3, 4, 2, 6, 5) (3, 6, 5, 1, 4) (3, 4, 5, 6, 2) (5, 4, 2, 6, 3)

Mutate (5, 3, 4, 6, 2) (2, 4, 6, 3, 5) (4, 3, 6, 5, 2) (2, 3, 4, 6, 5) (2, 3, 6, 4, 5) (3, 4, 5, 2, 6) (3, 5, 4, 6, 2) (4, 5, 3, 6, 2) (5, 4, 2, 3, 6) (4, 6, 3, 2, 5) (3, 4, 2, 6, 5) (3, 6, 5, 1, 4) (3, 4, 5, 6, 2) (5, 4, 2, 6, 3)

Eliminate (5, 3, 4, 6, 2) (2, 4, 6, 3, 5) (4, 3, 6, 5, 2) (2, 3, 4, 6, 5) (2, 3, 6, 4, 5) (3, 4, 5, 2, 6) (3, 5, 4, 6, 2) (4, 5, 3, 6, 2) (5, 4, 2, 3, 6) (4, 6, 3, 2, 5) (3, 4, 2, 6, 5) (3, 6, 5, 1, 4) (3, 4, 5, 6, 2) (5, 4, 2, 6, 3) Tend to kill off the worst ones.

Integrate (5, 3, 4, 6, 2) (2, 4, 6, 3, 5) (5, 4, 2, 6, 3) (3, 4, 5, 6, 2) (2, 3, 6, 4, 5) (3, 4, 5, 2, 6) (3, 5, 4, 6, 2) (4, 5, 3, 6, 2) (5, 4, 2, 3, 6) (4, 6, 3, 2, 5) (3, 4, 2, 6, 5) (3, 6, 5, 1, 4)

Restart (5, 3, 4, 6, 2) (2, 4, 6, 3, 5) (5, 4, 2, 6, 3) (3, 4, 5, 6, 2) (2, 3, 6, 4, 5) (3, 4, 5, 2, 6) (3, 5, 4, 6, 2) (4, 5, 3, 6, 2) (5, 4, 2, 3, 6) (4, 6, 3, 2, 5) (3, 4, 2, 6, 5) (3, 6, 5, 1, 4)

When to Use a GA n n n Alternate solutions are too slow or overly complicated Need an exploratory tool to examine new approaches Problem is similar to one that has already been successfully solved by using a GA Want to hybridize with an existing solution Benefits of the GA technology meet key problem requirements

n n SUMMARY Genetic Algorithms (GAs) implement optimization strategies based on simulation of the natural law of evolution of a species by natural selection The basic GA Operators are: Encoding Recombination Crossover Mutation GAs have been applied to a variety of function optimization problems, and have been shown to be highly effective in searching a large, poorly defined search space 49

THANK YOU