Genetic Algorithms Genetic Programming Lecture Outline Introduction Main

Genetic Algorithms + Genetic Programming

Lecture Outline Introduction Main Components Simple GA Steps Representation Scheme Fitness Function Genetic Operators – Crossover – Mutation Genetic Programming

Introduction First proposed by Fraser in 1957 Later by Bremermann in 1962 and Reed et al in 1967 Popularized by Holland in 1975 Genetic algorithms (GA) focuses on genetic evolution

Main Components The main components of GAs are: – Representation Scheme – Population – Fitness Function – Selection Scheme – Genetic Operators Reproduction Crossover Mutation – Stopping Conditions

GA Steps The series of operations carried out when implementing a canonical (basic) GA paradigm is: 1. Initialize the population. 2. Calculate fitness for each individual in the population. 3. Reproduce selected individuals to form a new population. 4. Perform crossover and mutation on the population. 5. Loop to step 2 until some condition is met.

Representation Scheme – used to encode each potential solution into a suitable representation needed by the genetic operations. – The encoded potential solution is called chromosome which consists of a sequence of genes. – The encoding of GA is viewed as a mapping between genotype level and phenotype level. – The conventional GA representation scheme is a binary representation with fixed length chromosome. – In this case each potential solution is represented as a binary string of fixed length L.

Population GA Population – Consists of a number of chromosomes (population size). – In conventional GA the population size is constant – The population size remains constant from generation to generation. – Initially, the first generation is generated randomly; – however, the subsequent generations are generated via genetic operations.

Fitness Function – The fitness function is the driving force of the evolution in GA. – It must be devised for each problem to be solved. – Given a particular chromosome, the fitness function returns a numerical value, which is supposed to be proportional to the utility or ability of the potential solution that chromosome represents. – For optimisation problem, the fitness function is simply the optimisation function.

Selection Scheme – used to select a chromosome in the population for genetic operations. – based on the survival-of-the-fittest, where the fitter the chromosome is, the higher its probability of being selected. – Many ways to perform selection in GAs, such as roulette wheel selection, Ranking selection, tournament selection, etc. – Recombination with replacement: If one offspring is generated, it may replace the worst parent Restriction can be imposed that offspring must be better Offspring may replace the worst individual in the population

Genetic Operators The genetic operators – The basis of GA evolution. – They recombine the chromosomes of the current population to produce the next generation. – Two operators are commonly implemented – Crossover operator: Probabilistically selects chromosomes from the current population based on their fitness values, and recombines them to generate offspring. Each offspring contains some genetic material from each of its parents. – Mutation: insures the population against permanent fixation. The common mutation is to randomly alter the value of a selected chromosome at a randomly selected position, and then copied it into the next generation.

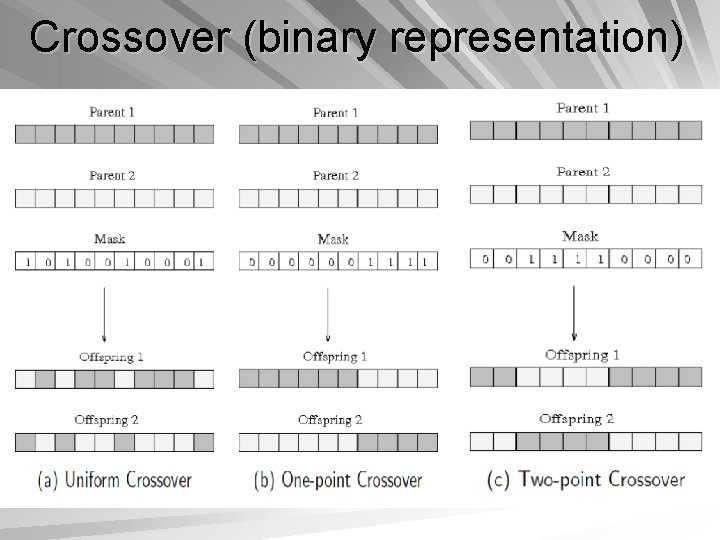
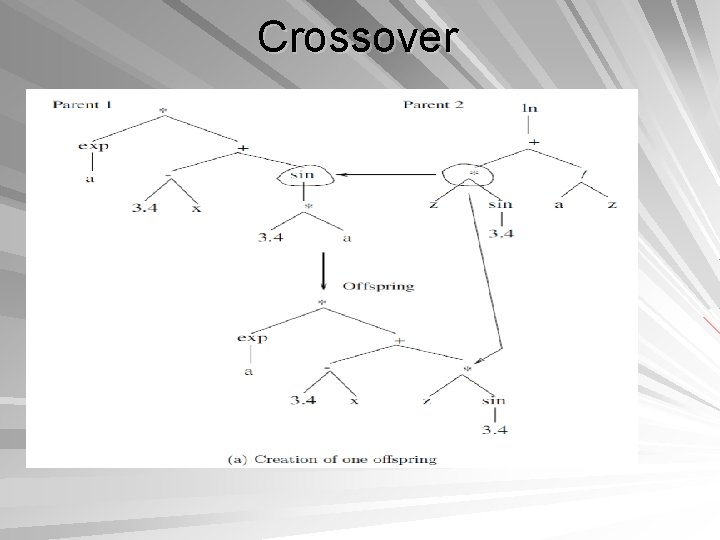
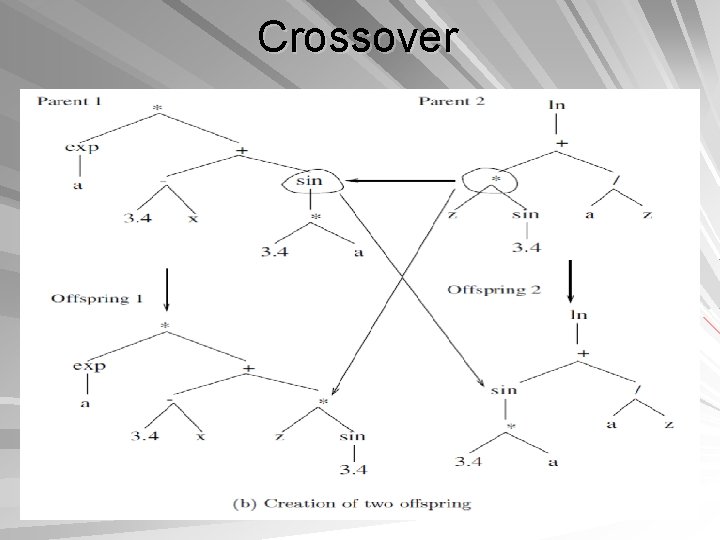
Crossover produce offspring by recombining genetic material from parents. two parents are used to produce one or two offspring Crossover occurs at a crossover probability, pc Selection of parents: use any selection scheme various crossover operators have been developed, according to the representation scheme

Crossover (binary representation)

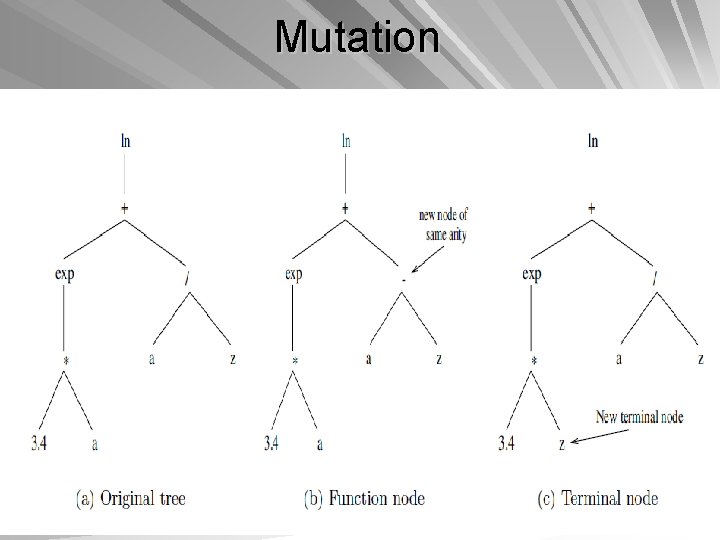
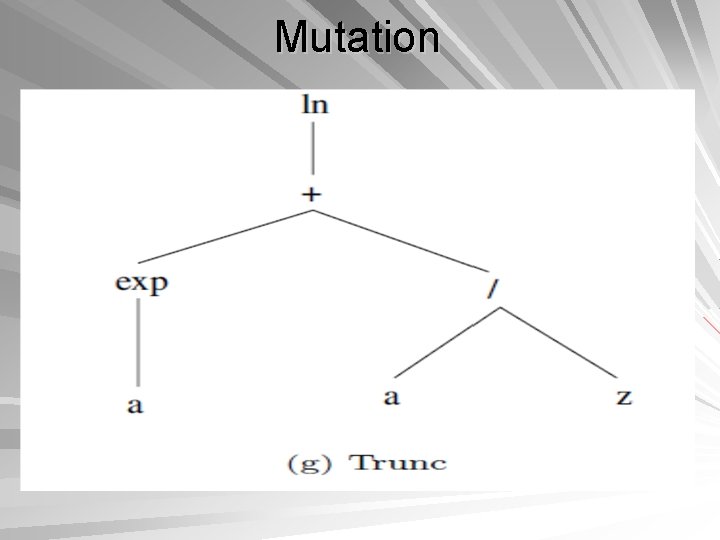
Mutation operator – – – introduces new genetic material into an existing individual adds diversity to the genetic characteristics of the population ensures that the full range of allele is accessible for each gene Applied at a mutation probability, pm Given that each gene is mutated at probability pm, the probability that an individual will be mutated is given by For Binary Representation

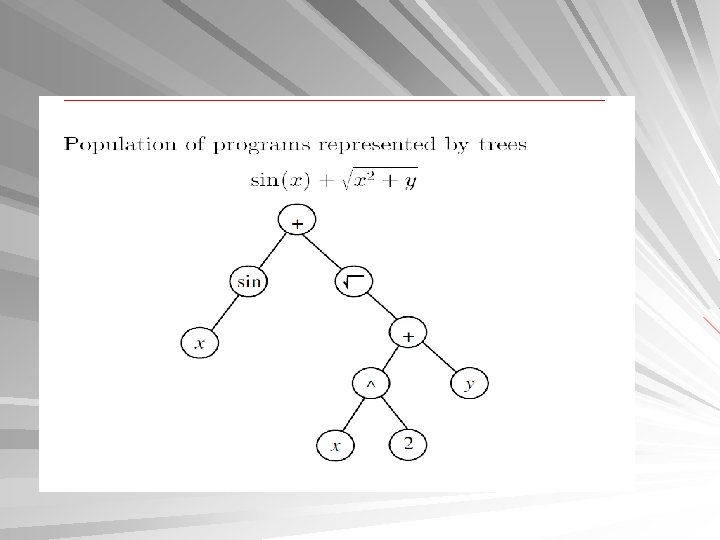
Genetic Programming Introduction Developed by Koza in the late 1980 s A specialization of GAs, where tree-based representations are used Originally developed to evolve computer programs As part of the fitness function, each program is executed to determine its outcomes

Tree Representation Each chromosome represents a solution as a tree Implications: – Adaptive individuals Size of individuals is not fixed Size depends on depth of tree and branching factor

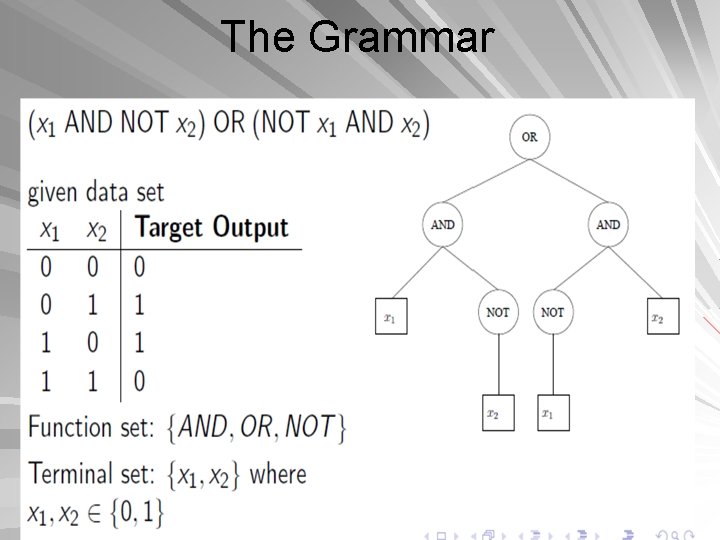
The Grammar Terminal set specifies all the variables and constants Function set contains all the functions that can be applied to the elements of the terminal set – – mathematical arithmetic Boolean decision structures such as if-then-else and loops Semantic rules which characterize valid solutions Example (1): Evolve Boolean expression

The Grammar

The Grammar Example (2): Evolve mathematical expression Terminal set: {a, x, z, 3. 4} with a, x, z R Function set: {−, +, *, /, sin, exp, ln}

Initial Population Randomly generated within the restrictions of a maximum depth and semantics as expressed by the given grammar For each individual, a root is randomly selected from the set of function elements Non-terminal nodes are randomly selected from the function set Terminal nodes selected from the terminal set Start with small initial trees

GP Operators

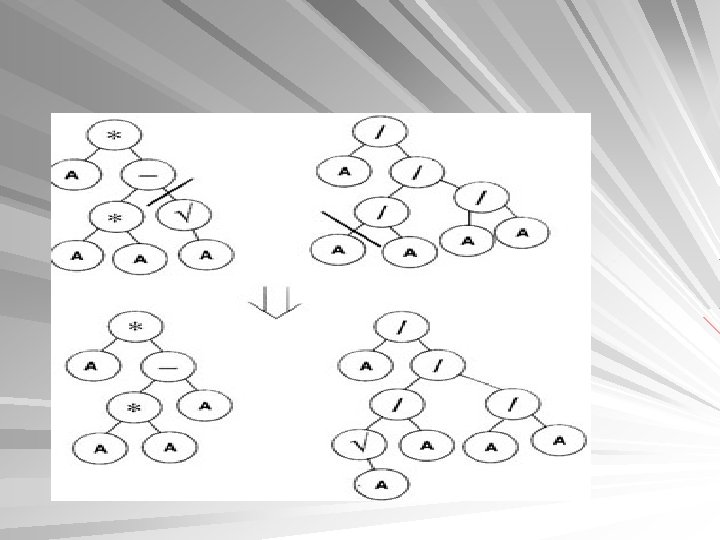
Crossover

Crossover

Mutation

Mutation