Genetic Algorithms Biological Evolution Lamarck and others Species

Genetic Algorithms

Biological Evolution • Lamarck and others: – Species “transmute” over time • Darwin: – Consistent, heritable variation among individuals in population – Natural selection of the fittest

Why GAs? • Evolution is known to be a successful, robust method for adaptation within biological systems. • GAs can search spaces of hypotheses containing complex interacting parts. – GAs have been applied successfully to a variety of learning tasks and optimization problems • GAs admit a natural implementation on massively parallel computers.

GAs - High Level Overview • Begin with a collection of initial hypotheses – a population • Then score the hypotheses (individuals) in the current population using a fitness function. • A new population is is then generated by probabilistically selecting the most fit individuals from the current population (survival of the fittest). • Some of these selected individuals are carried forward into the next generation intact. • Others are used as basis for creating new offspring individuals by applying genetic operations of crossover and mutation.

Formally GA(Fitness, Fitness threshold, p, r, m) • Initialize: P ← p random hypotheses • Evaluate: for each h in P, compute Fitness(h) • While [max Fitness(h)] < Fitness threshold 1. Select: Probabilistically select (1 − r)p members of P to add to Ps. 2. Crossover: Probabilistically select r·p/2 pairs of hypotheses from P. For each pair, <h 1, h 2>, produce two offspring by applying the Crossover operator. Add all offspring to Ps. 3. Mutate: Invert a randomly selected bit in m·p random members of Ps 4. Update: P ← Ps 5. Evaluate: for each h in P, compute Fitness(h) • Return the hypothesis from P that has the highest fitness.

Individual Selection • Roulette-Wheel Selection: Choose members from a population in a way that is proportional to their fitness. – Population’s total fitness score is represented by a pie chart, or roulette wheel. – Assign a slice of the wheel to each member of the population. • Size of the slice is proportional to that individual fitness score. – Select a member by spinning the ball and selecting the one at the point it stops. • Tournament Selection: Two members are chosen at random from a population. – With some predefined probability p the more fit of these two is then selected, and with probability 1 -p the less fit hypothesis is selected. Sometimes TS yields a more diverse population that RS.

Representing Hypotheses Represent (Outlook = Overcast Rain) (Wind = Strong) by Outlook Wind 011 10 Represent IF Wind = Strong THEN Play. Tennis = yes by Outlook Wind Play. Tennis 111 10 10 Don’t care for Outlook here.

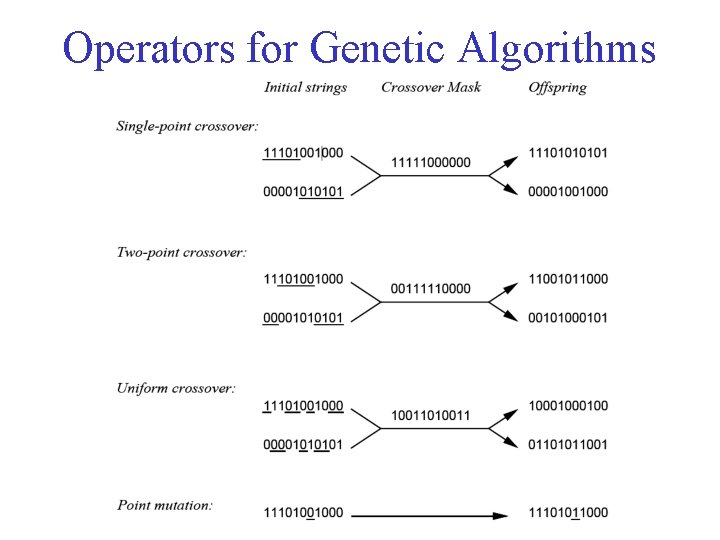
Operators for Genetic Algorithms

GABIL [De. Jong et al. 1993] • Learn a set of rules Representation: • Each hypothesis is a set of rules • To represent a set of rules, the bit-string representation of individual rules are concatenated Example IF a 1 = T AND a 2 = F THEN c = T; IF a 2 = T THEN c = F a 1 a 2 c 10 01 1 a 2 c 11 10 0

GABIL Fitness function: Fitness(h) = (correct(h))2 correct(h): the percent of all training examples correctly classified

GABIL: Genetic operators • Use the standard mutation operator • Crossover: extension of the two-point crossover operator – want variable length rule sets – want only well-formed bitstring hypotheses • Crossover with variable-length bitstrings 1. choose two crossover points for h 1. Let d 1 (d 2) be the distance to the rule boundary immediately to its left. 2. now restrict points in h 2 to those that have the same d 1 and d 2 value

GABIL: Crossover h 1 : h 2 : a 1 a 2 c 10 01 11 0 a 1 a 2 c 11 10 01 0 Suppose crossover points for h 1, are after bits 1, 8 (d 1=1; d 2=3) a 1 a 2 c h 1 : 1[0 01 1 11 1]0 0 Allowed pairs of crossover points for h 2 are <1; 3>, <1; 8>, <6; 8>. If pair <1; 3> is chosen, a 1 a 2 c h 2 : 0[1 1]1 0 10 01 0 the result is:

GABIL: Crossover h 3 : a 1 a 2 c 11 10 0 h 4 : a 1 a 2 c 00 01 1 a 2 c 11 11 0 a 1 a 2 c 10 01 0