GENETIC ALGORITHMS AND GENETIC PROGRAMMING John R Koza

GENETIC ALGORITHMS AND GENETIC PROGRAMMING

John R. Koza Consulting Professor (Medical Informatics) Department of Medicine School of Medicine Consulting Professor Department of Electrical Engineering School of Engineering Stanford University Stanford, California 94305 koza@stanford. edu http: //www. smi. stanford. edu/people/koza/

DEFINITION OF THE GENETIC ALGORITHM (GA) The genetic algorithm is a probabalistic search algorithm that iteratively transforms a set (called a population) of mathematical objects (typically fixed-length binary character strings), each with an associated fitness value, into a new population of offspring objects using the Darwinian principle of natural selection and using operations that are patterned after naturally occurring genetic operations, such as crossover (sexual recombination) and mutation.

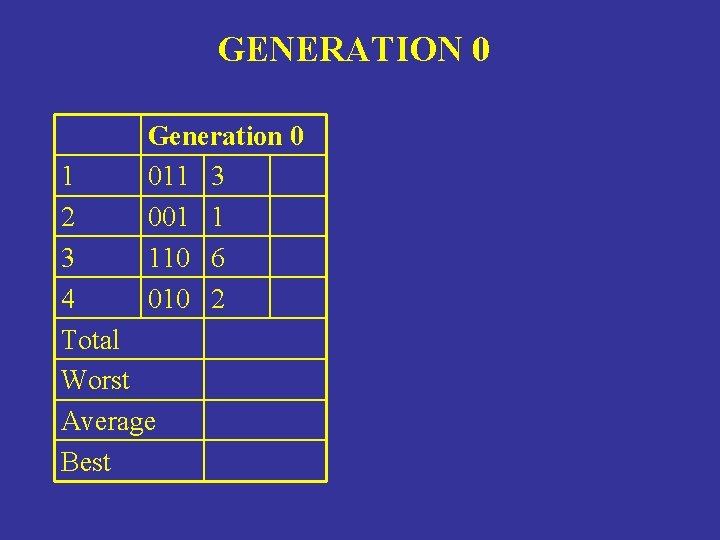
GENETIC ALGORITHM (GA) Generation 0 Generation 1 Individuals Fitness Offspring 011 $3 111 001 $1 010 110 $6 110 010 $2 010

HAMBURGER RESTAURANT PROBLEM • Price 1 = $ 0. 50 price 0 = $10. 00 price • Drink 1 = Coca Cola 0 = Wine • Ambiance 1 = Fast snappy service 0 = Leisurely service with tuxedoed waiter

CHROMOSOME (GENOME) OF THE GLOBAL OPTIMUM Mc. DONALD's 1 1 1

THE SEARCH SPACE 1 2 3 4 5 6 7 8 000 001 010 011 100 101 110 111 • Alphabet size K=2, Length L=3 • Size of search space: KL=2 L=23=8

IMPRACTICALITY OF RANDOM OR ENUMERATIVE SEARCH • 81 -bit problems are very small for GA • However, even if L is as small as 81, 281 ~ 1027 = number of nanoseconds since the beginning of the universe 15 billion years ago

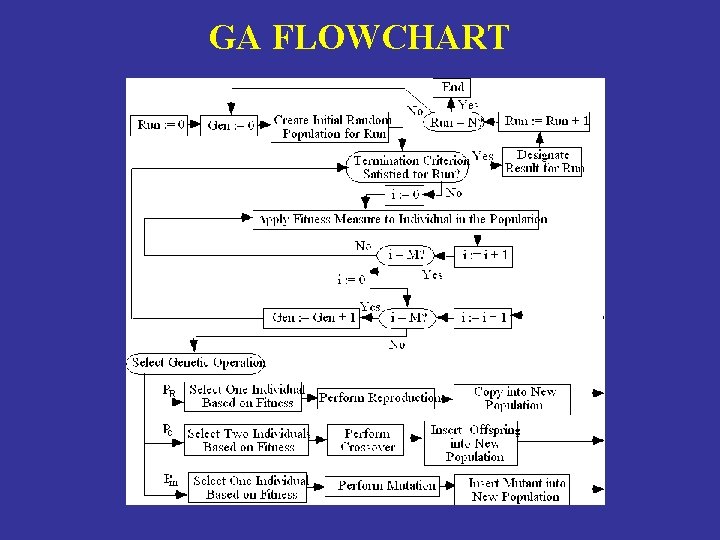
GA FLOWCHART

GENERATION 0 Generation 0 011 3 001 1 110 6 010 2 1 2 3 4 Total Worst Average Best

DEFINITION OF THE GENETIC ALGORITHM (GA) The genetic algorithm is a probabalistic search algorithm that iteratively transforms a set (called a population) of mathematical objects (typically fixed-length binary character strings), each with an associated fitness value, into a new population of offspring objects using the Darwinian principle of natural selection and using operations that are patterned after naturally occurring genetic operations, such as crossover (sexual recombination) and mutation.

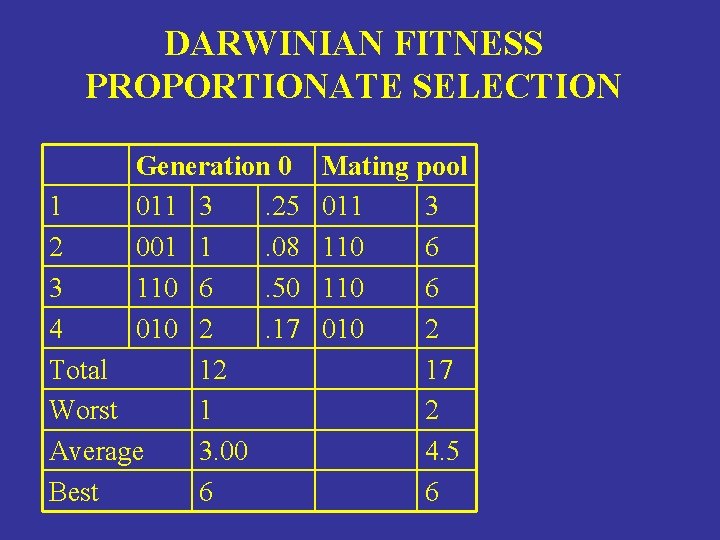
PROBABILISTIC SELECTION BASED ON FITNESS • • • Better individuals are preferred Best is not always picked Worst is not necessarily excluded Nothing is guaranteed Mixture of greedy exploitation and adventurous exploration • Similarities to simulated annealing (SA)

DARWINIAN FITNESS PROPORTIONATE SELECTION Generation 0 1 011 3. 25 2 001 1. 08 3 110 6. 50 4 010 2. 17 Total 12 Worst 1 Average 3. 00 Best 6 Mating pool 011 3 110 6 010 2 17 2 4. 5 6

DEFINITION OF THE GENETIC ALGORITHM (GA) The genetic algorithm is a probabalistic search algorithm that iteratively transforms a set (called a population) of mathematical objects (typically fixed-length binary character strings), each with an associated fitness value, into a new population of offspring objects using the Darwinian principle of natural selection and using operations that are patterned after naturally occurring genetic operations, such as crossover (sexual recombination) and mutation.

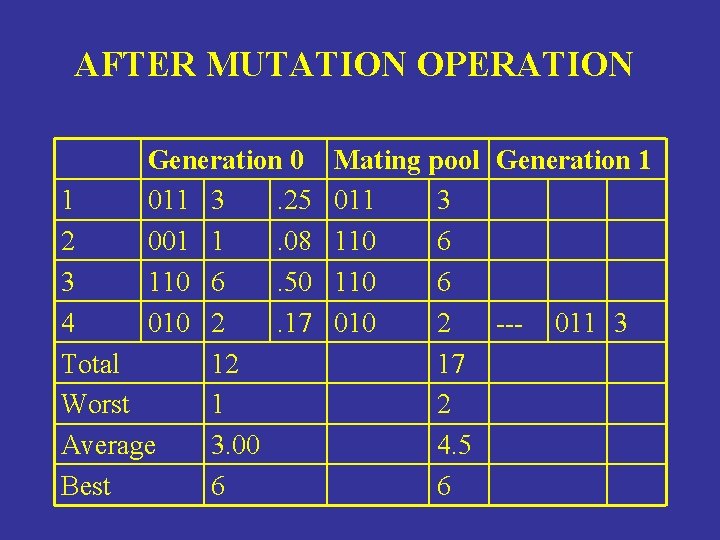
MUTATION OPERATION • Parent chosen probabilistically based on fitness Parent 010 • Mutation point chosen at random Parent --0 • One offspring Offspring 011

AFTER MUTATION OPERATION Generation 0 1 011 3. 25 2 001 1. 08 3 110 6. 50 4 010 2. 17 Total 12 Worst 1 Average 3. 00 Best 6 Mating pool Generation 1 011 3 110 6 010 2 --- 011 3 17 2 4. 5 6

CROSSOVER OPERATION • 2 parents chosen probabilistically based on fitness P a r e n t 1 P a r e n t 2

CROSSOVER (CONTINUED) • Interstitial point picked at random Fragment 1 01 - Fragment 2 11 - • 2 remainders Remainder 1 Remainder 2 --1 --0 • 2 offspring produced by crossover Offspring 1 111 Offspring 2 010

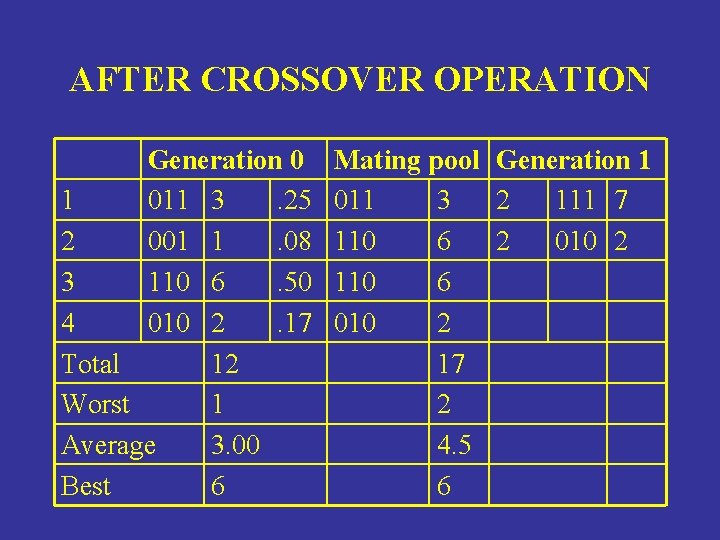
AFTER CROSSOVER OPERATION Generation 0 1 011 3. 25 2 001 1. 08 3 110 6. 50 4 010 2. 17 Total 12 Worst 1 Average 3. 00 Best 6 Mating pool Generation 1 011 3 2 111 7 110 6 2 010 2 110 6 010 2 17 2 4. 5 6

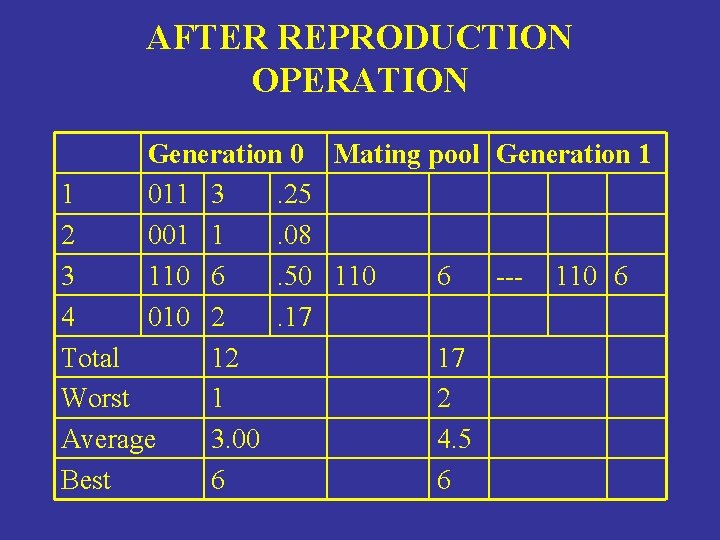
AFTER REPRODUCTION OPERATION Generation 0 Mating pool Generation 1 1 011 3. 25 2 001 1. 08 3 110 6. 50 110 6 --- 110 6 4 010 2. 17 Total 12 17 Worst 1 2 Average 3. 00 4. 5 Best 6 6

DEFINITION OF THE GENETIC ALGORITHM (GA) The genetic algorithm is a probabalistic search algorithm that iteratively transforms a set (called a population) of mathematical objects (typically fixed-length binary character strings), each with an associated fitness value, into a new population of offspring objects using the Darwinian principle of natural selection and using operations that are patterned after naturally occurring genetic operations, such as crossover (sexual recombination) and mutation.

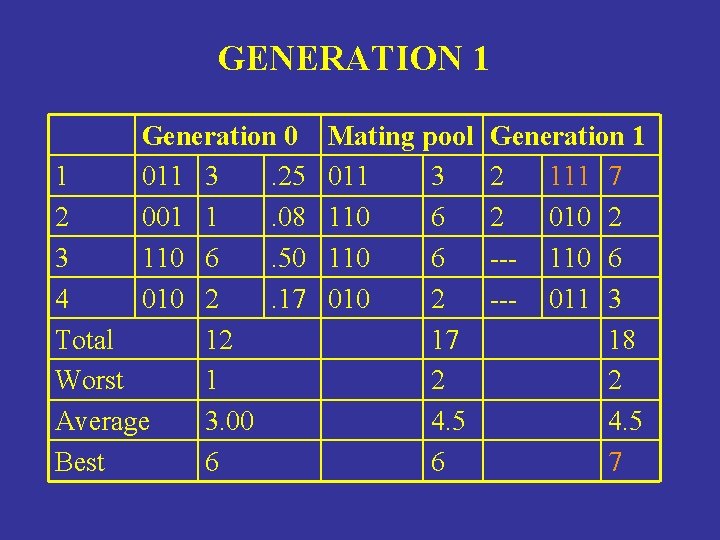
GENERATION 1 Generation 0 1 011 3. 25 2 001 1. 08 3 110 6. 50 4 010 2. 17 Total 12 Worst 1 Average 3. 00 Best 6 Mating pool 011 3 110 6 010 2 17 2 4. 5 6 Generation 1 2 111 7 2 010 2 --- 110 6 --- 011 3 18 2 4. 5 7

PROBABILISTIC STEPS • The initial population is typically random • Probabilistic selection based on fitness - Best is not always picked - Worst is not necessarily excluded • Random picking of mutation and crossover points • Often, there is probabilistic scenario as part of the fitness measure

GENETIC PROGRAMMING

THE CHALLENGE "How can computers learn to solve problems without being explicitly programmed? In other words, how can computers be made to do what is needed to be done, without being told exactly how to do it? " Attributed to Arthur Samuel (1959)

CRITERION FOR SUCCESS "The aim [is]. . . to get machines to exhibit behavior, which if done by humans, would be assumed to involve the use of intelligence. “ Arthur Samuel (1983)

REPRESENTATIONS • Decision trees • If-then production rules • Horn clauses • Neural nets • Bayesian networks • Frames • Propositional logic • Binary decision diagrams • Formal grammars • Coefficients for polynomials • Reinforcement learning tables • Conceptual clusters • Classifier systems

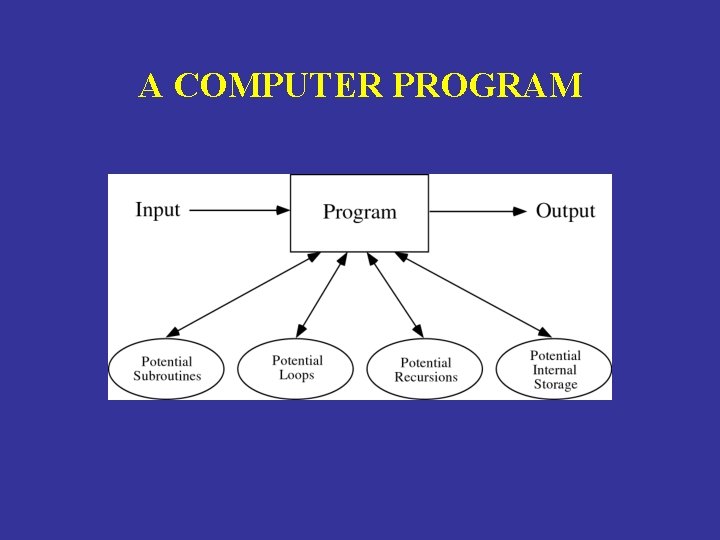
A COMPUTER PROGRAM

GENETIC PROGRAMMING (GP) • GP applies the approach of the genetic algorithm to the space of possible computer programs • Computer programs are the lingua franca for expressing the solutions to a wide variety of problems • A wide variety of seemingly different problems from many different fields can be reformulated as a search for a computer program to solve the problem.

GP MAIN POINTS • Genetic programming now routinely delivers high-return human-competitive machine intelligence. • Genetic programming is an automated invention machine. • Genetic programming has delivered a progression of qualitatively more substantial results in synchrony with five approximately order-of-magnitude increases in the expenditure of computer time.

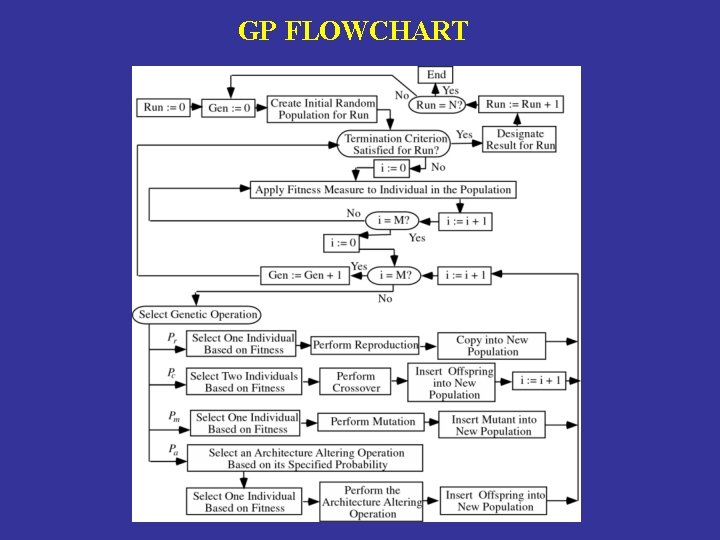
GP FLOWCHART

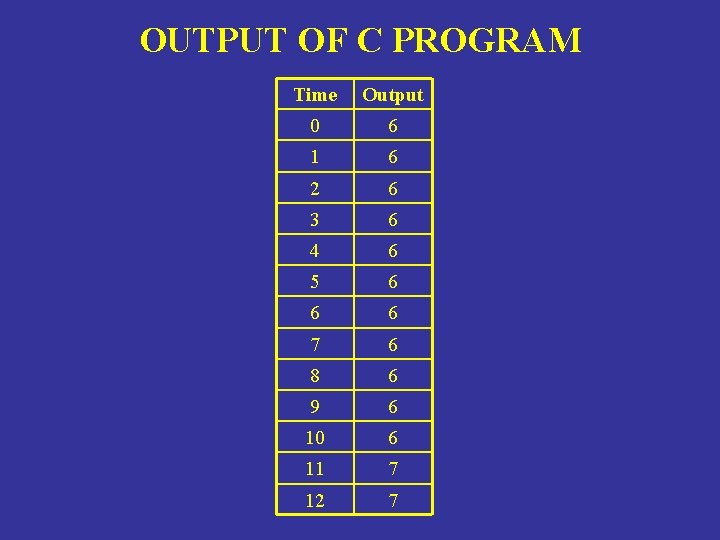
A COMPUTER PROGRAM IN C int foo (int time) { int temp 1, temp 2; if (time > 10) temp 1 = 3; else temp 1 = 4; temp 2 = temp 1 + 2; return (temp 2); }

OUTPUT OF C PROGRAM Time Output 0 6 1 6 2 6 3 6 4 6 5 6 6 6 7 6 8 6 9 6 10 6 11 7 12 7

PROGRAM TREE (+ 1 2 (IF (> TIME 10) 3 4))

CREATING RANDOM PROGRAMS

CREATING RANDOM PROGRAMS • Available functions F = {+, -, *, %, IFLTE} • Available terminals T = {X, Y, Random-Constants} • The random programs are: – Of different sizes and shapes – Syntactically valid – Executable

GP GENETIC OPERATIONS • • Reproduction Mutation Crossover (sexual recombination) Architecture-altering operations

MUTATION OPERATION

MUTATION OPERATION • • Select 1 parent probabilistically based on fitness Pick point from 1 to NUMBER-OF-POINTS Delete subtree at the picked point Grow new subtree at the mutation point in same way as generated trees for initial random population (generation 0) • The result is a syntactically valid executable program • Put the offspring into the next generation of the population

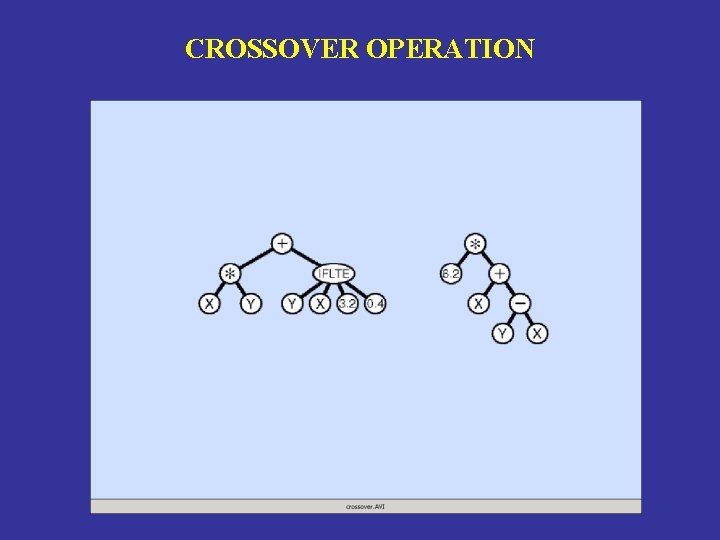
CROSSOVER OPERATION

CROSSOVER OPERATION • Select 2 parents probabilistically based on fitness • Randomly pick a number from 1 to NUMBER-OFPOINTS for 1 st parent • Independently randomly pick a number for 2 nd parent • The result is a syntactically valid executable program • Put the offspring into the next generation of the population • Identify the subtrees rooted at the two picked points

REPRODUCTION OPERATION • Select parent probabilistically based on fitness • Copy it (unchanged) into the next generation of the population

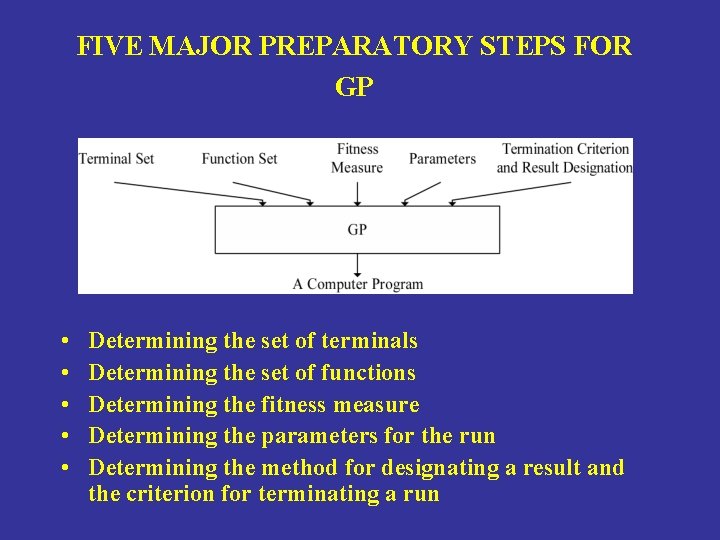
FIVE MAJOR PREPARATORY STEPS FOR GP • • • Determining the set of terminals Determining the set of functions Determining the fitness measure Determining the parameters for the run Determining the method for designating a result and the criterion for terminating a run

PREPARATORY STEPS Objective: Find a computer program with one input (independent variable X) whose output equals the given data 1 Terminal set: T = {X, Random-Constants} 2 Function set: F = {+, 3 Fitness: The sum of the absolute value of the differences between the candidate program’s output and the given data (computed over numerous values of the independent variable x from – 1. 0 to +1. 0) 4 Parameters: Population size M = 4 5 Termination: An individual emerges whose sum of absolute errors is less than 0. 1 -, *, %}

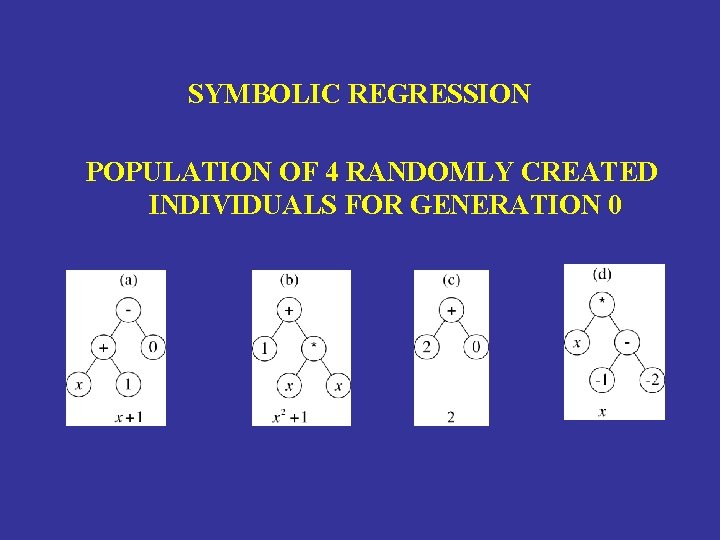
SYMBOLIC REGRESSION POPULATION OF 4 RANDOMLY CREATED INDIVIDUALS FOR GENERATION 0

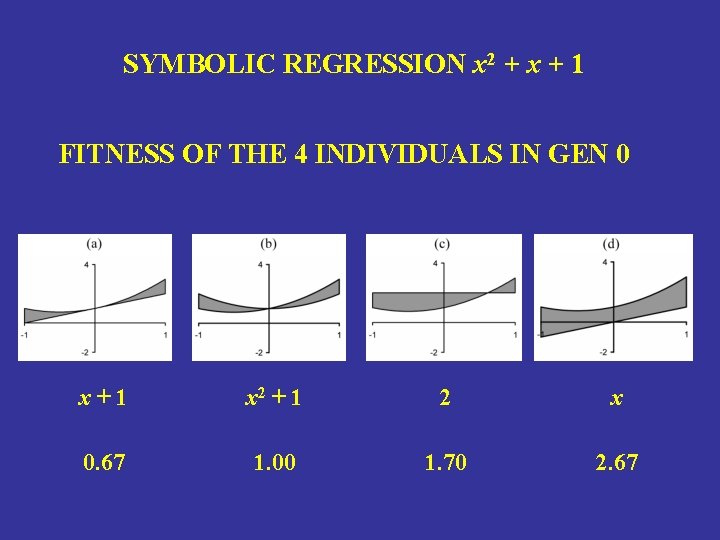
SYMBOLIC REGRESSION x 2 + x + 1 FITNESS OF THE 4 INDIVIDUALS IN GEN 0 x+1 x 2 + 1 2 x 0. 67 1. 00 1. 70 2. 67

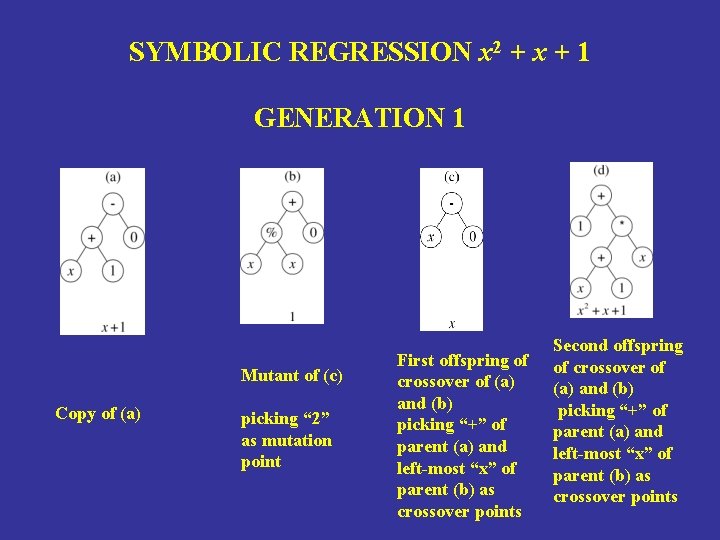
SYMBOLIC REGRESSION x 2 + x + 1 GENERATION 1 Mutant of (c) Copy of (a) picking “ 2” as mutation point First offspring of crossover of (a) and (b) picking “+” of parent (a) and left-most “x” of parent (b) as crossover points Second offspring of crossover of (a) and (b) picking “+” of parent (a) and left-most “x” of parent (b) as crossover points

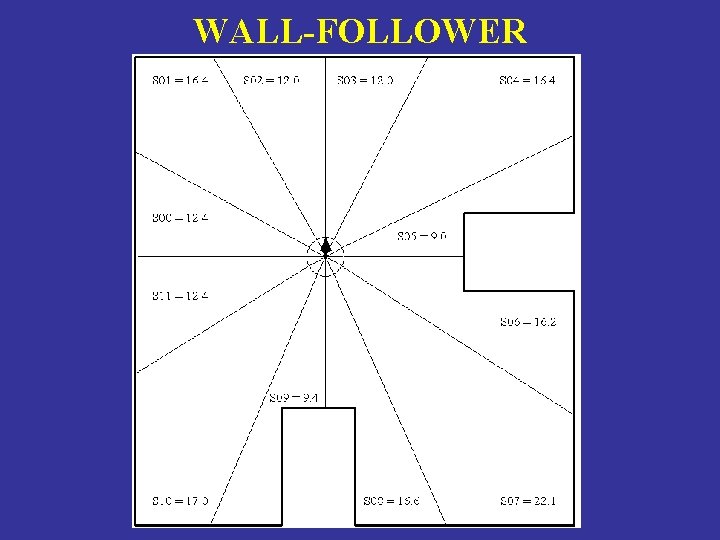
WALL-FOLLOWER

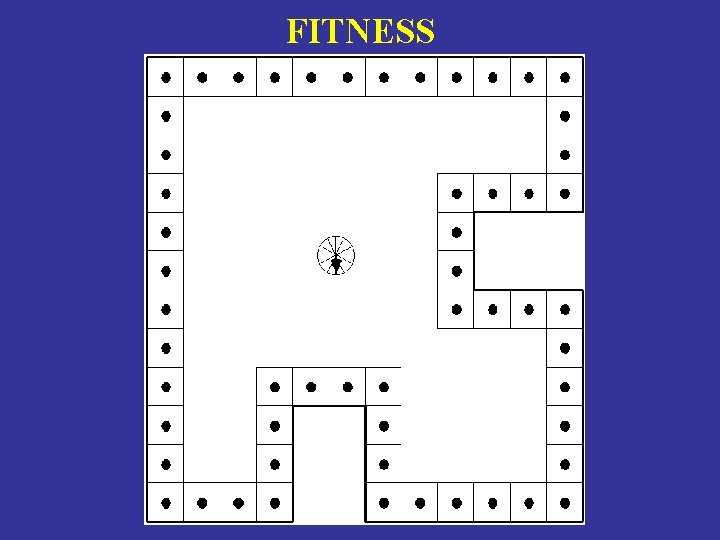
FITNESS

BEST OF GENERATION 57

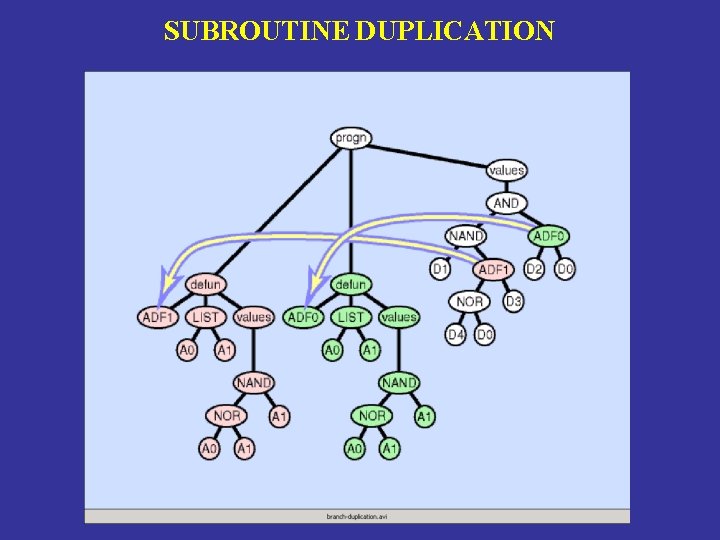
SUBROUTINE DUPLICATION

SUBROUTINE CREATION

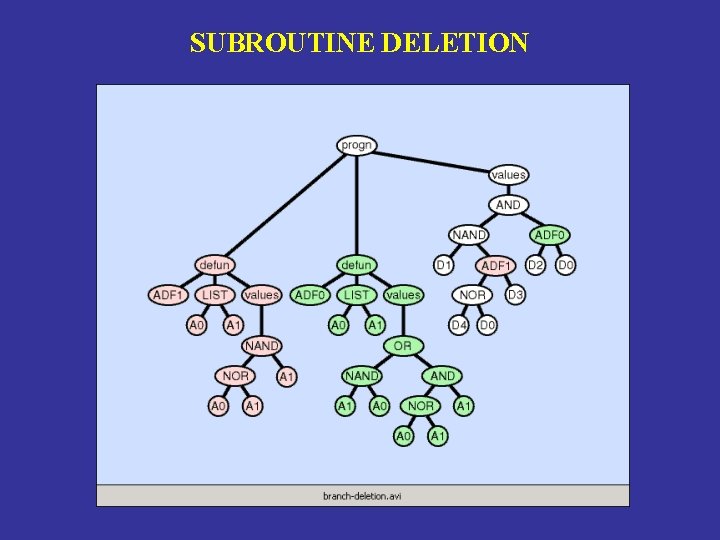
SUBROUTINE DELETION

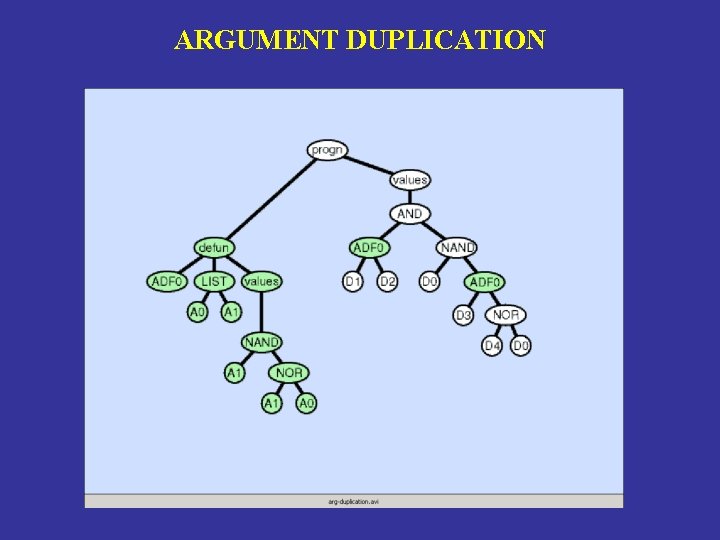
ARGUMENT DUPLICATION

ARGUMENT DELETION

16 ATTRIBUTES OF A SYSTEM FOR AUTOMATICALLY CREATING COMPUTER PROGRAMS • Starts with "What needs to be done" • Tells us "How to do it" • Produces a computer program • Automatic determination of program size • Code reuse • Parameterized reuse • Internal storage • Iterations, loops, and recursions • Self-organization of hierarchies • Automatic determination of program architecture • Wide range of programming constructs • Well-defined • Problem-independent • Wide applicability • Scalable • Competitive with humanproduced results

PROGRESSION OF QUALITATIVELY MORE SUBSTANTIAL RESULTS PRODUCED BY GP • • • Toy problems Human-competitive non-patent results 20 th-century patented inventions 21 st-century patented inventions Patentable new inventions

GP AS AN INVENTION MACHINE

NASA EVOLVED ANTENNA To be on satellite to be launched in 2004

CHARACTERISTICS SUGGESTING USE OF GP (1) discovering the size and shape of the solution, (2) reusing substructures, (3) discovering the number of substructures, (4) discovering the nature of the hierarchical references among substructures, (5) passing parameters to a substructure, (6) discovering the type of substructures (e. g. , subroutines, iterations, loops, recursions, or storage), (7) discovering the number of arguments possessed by a substructure, (8) maintaining syntactic validity and locality by means of a developmental process, or (9) discovering a general solution in the form of a parameterized topology containing free variables

DESIGNING A GIRAFFE • • • Long neck Long tongue Vegetable-digesting enzymes in stomach 4 legs Long legs Brown coloration

THE DESIGN OF A GOOD GIRAFE Neck length Tongue length Carnivorous? Number Leg of legs length 15. 11 feet 14 inches No 4 9. 96 feet Brown Floating point Integer Floating Categorical point Boolean Coloration

NON-LINEARITY — GIRAFE • Taken one-by-one, some gene values found in a giraffe, such as the long neck contribute (alone) negatively to fitness – requires considerable material to construct – requires considerable energy to maintain – prone to injury (thereby hurting rate of survival and reproduction) • Thus, maximizing any one variable will not lead to the global optimum solution

NON-LINEARITY (CONTINUED) • When the variables are taken in pairs (there are 15 possible pairs), many combinations of pairs (e. g. , Long neck and long tongue) are doubly detrimental

NON-LINEARITY (CONTINUED) • But, certain combinations of traits, when taken together, are "co-adapted sets of alleles" that yield a very fit animal for eating high acacia leaves in the jungle environment, having good camouflage, having high escape velocity when faced with predators, and exploiting a niche (and avoiding competition) with other animals feeding on low-hanging vegetation

SEARCH METHODS IN GENERAL • • • Initial structure(s) Fitness measure Operations for creating new structures Parameters Termination criterion and method of designating the result

SPACE WITH MANY LOCAL OPTIMA

SEARCH METHODS • Blind random search does not use acquired information in deciding on the future direction of the search • Hill combing and gradient descent use acquired information; however, they are prone to becoming trapped on local optima • The previous point is especially true for nontrivial search spaces

7 DIFFERENCES BETWEEN GP AND ARTIFICIAL INTELLIGENCE AND MACHINE LEARNING APPROACHES

REPRESENTATION Genetic programming overtly conducts it search for a solution to the given problem in program space

ROLE OF POINT-TO-POINT TRANSFORMATIONS IN THE SEARCH Genetic programming does not conduct its search by transforming a single point in the search space into another single point, but instead transforms a set of points into another set of points

ROLE OF HILL CLIMBING IN THE SEARCH Genetic programming does not rely exclusively on greedy hill climbing to conduct its search, but instead allocates a certain number of trials, in a principled way, to choices that are known to be inferior

DETERMINISM IN THE SEARCH Genetic programming conducts its search probabilistically

ROLE OF AN EXPLICIT KNOWLEDGE BASE Genetic programming does NOT make use of a knowledge base

ROLE OF FORMAL LOGIC IN THE SEARCH Genetic programming does not utilize formal logic in it’s search strategy. Contradictory alternatives are created and actively maintained.

UNDERPINNINGS OF THE TECHNIQUE Biologically inspired

TURING (1948) Turing made the connection between searches and the challenge of getting a computer to solve a problem without explicitly programming it in his 1948 essay “Intelligent Machines” "Further research into intelligence of machinery will probably be very greatly concerned with 'searches'. . . “

TURING’S 3 APPROACHES TO MACHINE INTELLIGENCE (1948) LOGIC-BASED SEARCH One approach that Turing identified is a search through the space of integers representing candidate computer programs.

TURING’S 3 APPROACHES (CONTINUED) CULTURAL SEARCH A second approach is the "cultural search“ which relies on knowledge and expertise acquired over a period of years from others (akin to present-day knowledgebased systems).

TURING’S 3 APPROACHES (CONTINUED) GENETICAL OR EVOLUTIONARY SEARCH "There is the genetical or evolutionary search by which a combination of genes is looked for, the criterion being the survival value. “

TURING (1950) From Turing’s 1950 paper "Computing Machinery and Intelligence" … “We cannot expect to find a good childmachine at the first attempt. One must experiment with teaching one such machine and see how well it learns. One can then try another and see if it is better or worse. There is an obvious connection between this process and evolution, by the identifications”

TURING (1950) (CONTINUED) “Structure of the child machine = Hereditary material “Changes of the child machine = Mutations “Natural selection = of the experimenter” Judgment