Generating Inputs to the TDOA simulator By Andrew

Generating Inputs to the TDOA simulator By Andrew De. Vries Progress Report 10/22
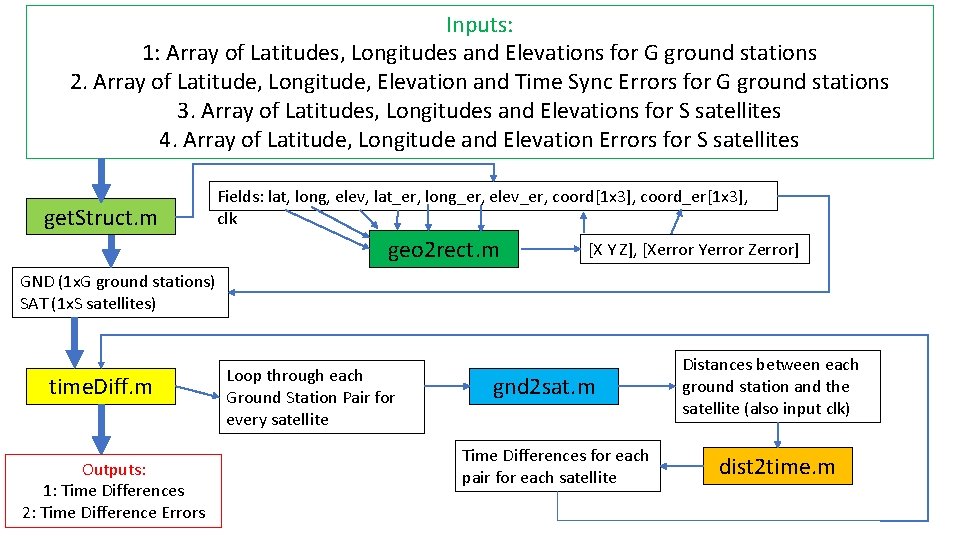
Inputs: 1: Array of Latitudes, Longitudes and Elevations for G ground stations 2. Array of Latitude, Longitude, Elevation and Time Sync Errors for G ground stations 3. Array of Latitudes, Longitudes and Elevations for S satellites 4. Array of Latitude, Longitude and Elevation Errors for S satellites get. Struct. m Fields: lat, long, elev, lat_er, long_er, elev_er, coord[1 x 3], coord_er[1 x 3], clk geo 2 rect. m [X Y Z], [Xerror Yerror Zerror] GND (1 x. G ground stations) SAT (1 x. S satellites) time. Diff. m Outputs: 1: Time Differences 2: Time Difference Errors Loop through each Ground Station Pair for every satellite gnd 2 sat. m Time Differences for each pair for each satellite Distances between each ground station and the satellite (also input clk) dist 2 time. m
![S 1 Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] S 1 Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m]](http://slidetodoc.com/presentation_image_h2/77e6e5cc883597f4dc8bce6b2808a7bf/image-3.jpg)
S 1 Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Inputs: A Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk sync [s] C Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk sync [s] B Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk sync [s] D Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk sync [s] S 2 Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m]
![A Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk A Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk](http://slidetodoc.com/presentation_image_h2/77e6e5cc883597f4dc8bce6b2808a7bf/image-4.jpg)
A Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk sync All information captured in GND structure! C Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk sync B Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk sync D Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] Clk sync
![S 1 Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] S 1 Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m]](http://slidetodoc.com/presentation_image_h2/77e6e5cc883597f4dc8bce6b2808a7bf/image-5.jpg)
S 1 Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m] All information captured in SAT structure! S 2 Lat, Lat error [deg] Long, Long error [deg] Elev, Elev error [m]
![Outputs: Time Difference Matrix Time Difference [s] Time Difference Error [s] N satellites G Outputs: Time Difference Matrix Time Difference [s] Time Difference Error [s] N satellites G](http://slidetodoc.com/presentation_image_h2/77e6e5cc883597f4dc8bce6b2808a7bf/image-6.jpg)
Outputs: Time Difference Matrix Time Difference [s] Time Difference Error [s] N satellites G Ground Stations S 1 S 2 … A-B A-B error A-C A-C error A-D A-D error . . B-C B-C error . . B-D B-D error . . C-D C-D error (G-1)-G error SN

Notes: • time. Diff can run with any size GND and SAT structures • The coordinate conversion assumes a spherical earth • Satellite position is absolute Lat and Long, not azimuth and elevation • The elevations values are in meters above sea level

The TDo. A simulator By Anthony Iannuzzi Progress Report 10/22
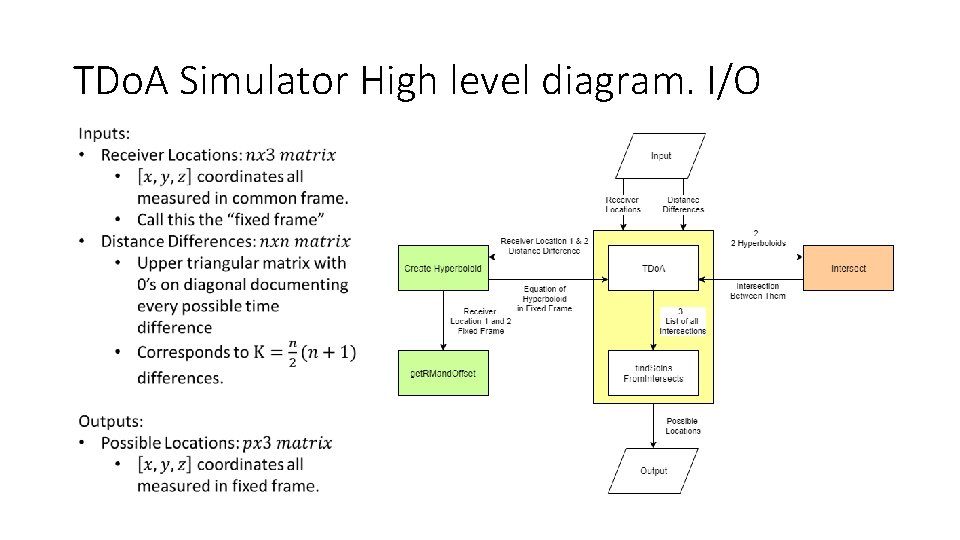
TDo. A Simulator High level diagram. I/O
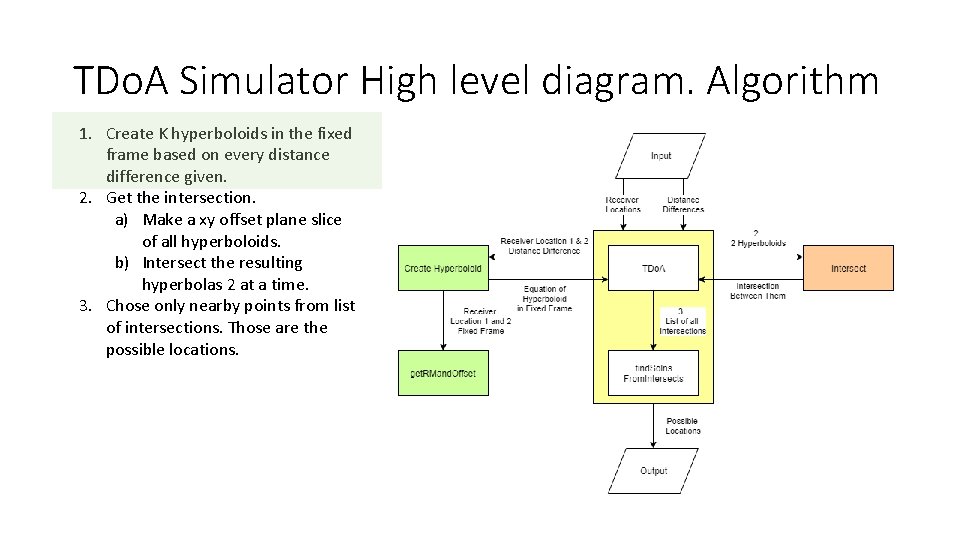
TDo. A Simulator High level diagram. Algorithm 1. Create K hyperboloids in the fixed frame based on every distance difference given. 2. Get the intersection. a) Make a xy offset plane slice of all hyperboloids. b) Intersect the resulting hyperbolas 2 at a time. 3. Chose only nearby points from list of intersections. Those are the possible locations.
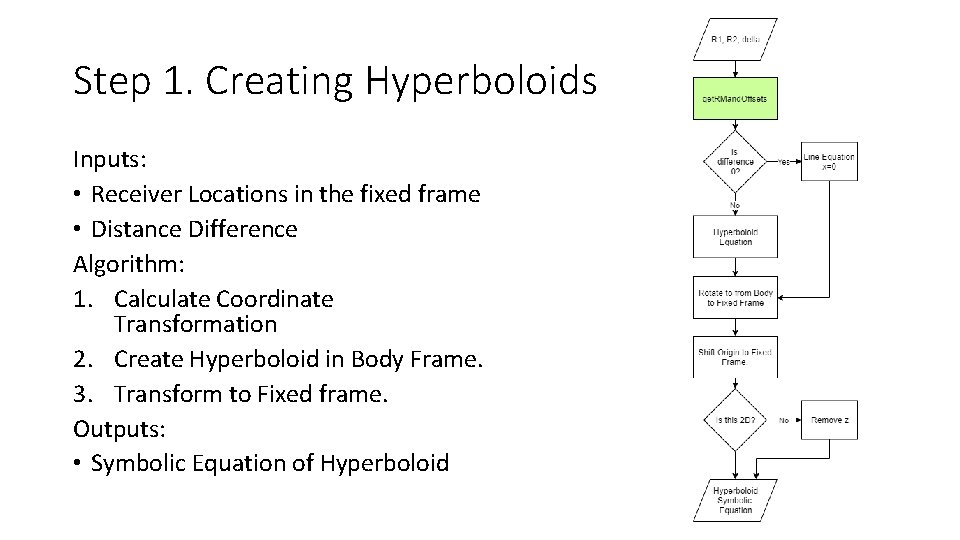
Step 1. Creating Hyperboloids Inputs: • Receiver Locations in the fixed frame • Distance Difference Algorithm: 1. Calculate Coordinate Transformation 2. Create Hyperboloid in Body Frame. 3. Transform to Fixed frame. Outputs: • Symbolic Equation of Hyperboloid
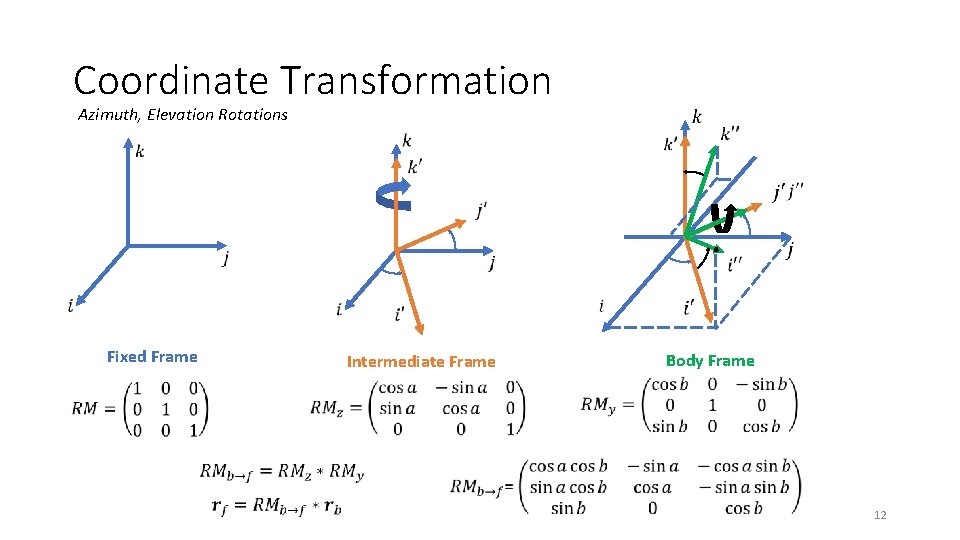
Coordinate Transformation Azimuth, Elevation Rotations Fixed Frame Intermediate Frame Body Frame 12
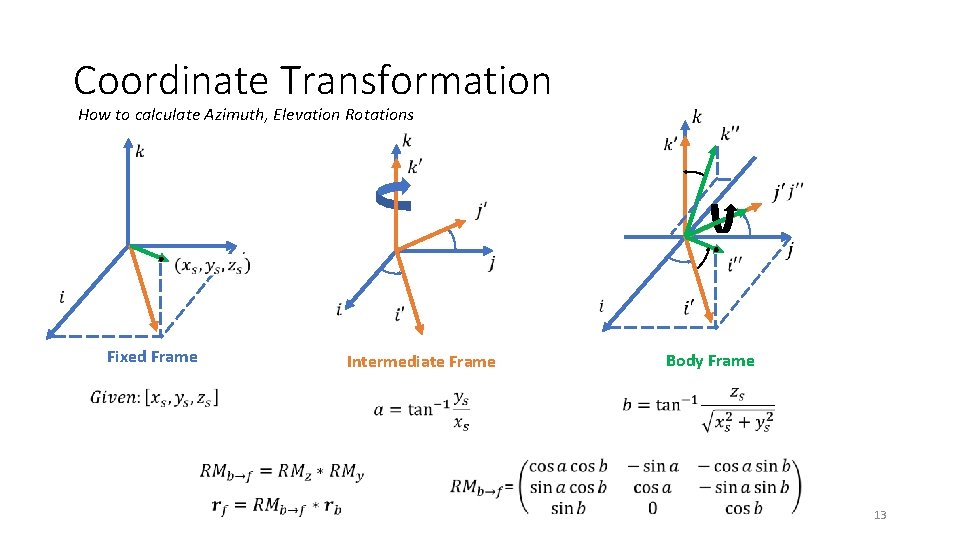
Coordinate Transformation How to calculate Azimuth, Elevation Rotations Fixed Frame Intermediate Frame Body Frame 13
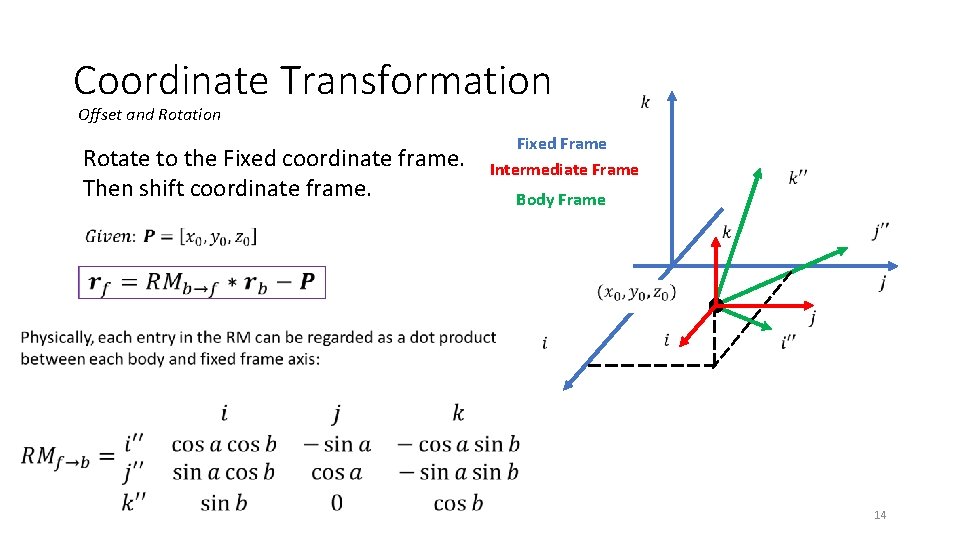
Coordinate Transformation Offset and Rotation Rotate to the Fixed coordinate frame. Then shift coordinate frame. Fixed Frame Intermediate Frame Body Frame 14
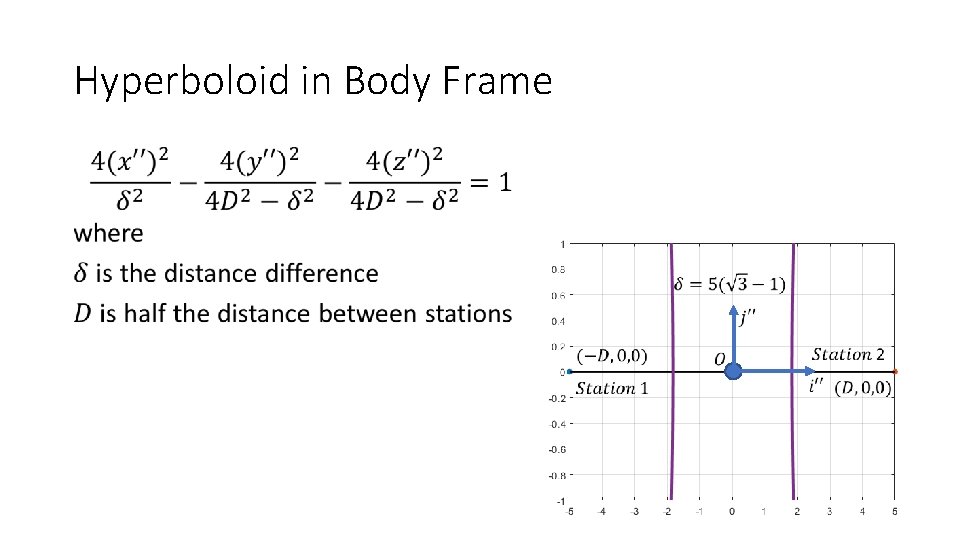
Hyperboloid in Body Frame •

Hyperboloid in Fixed Frame •
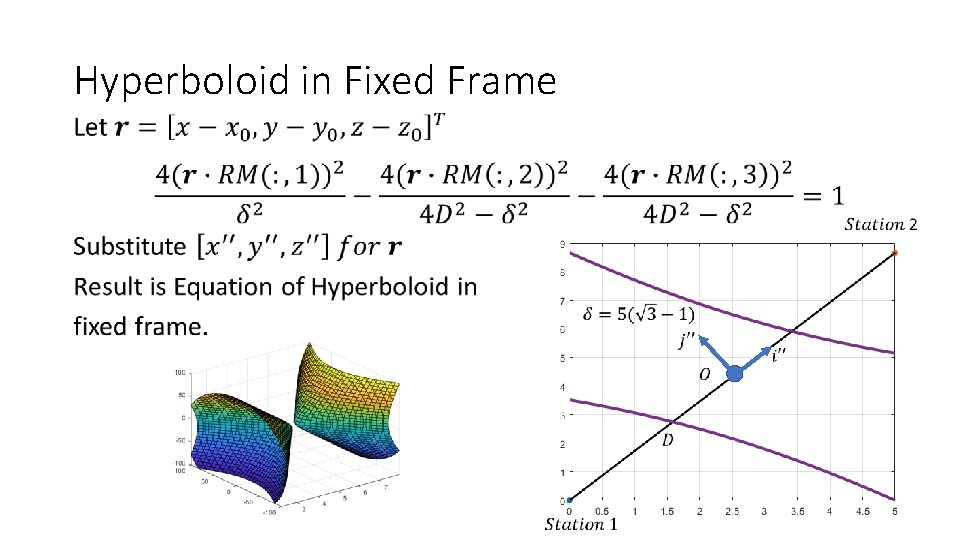
Hyperboloid in Fixed Frame •
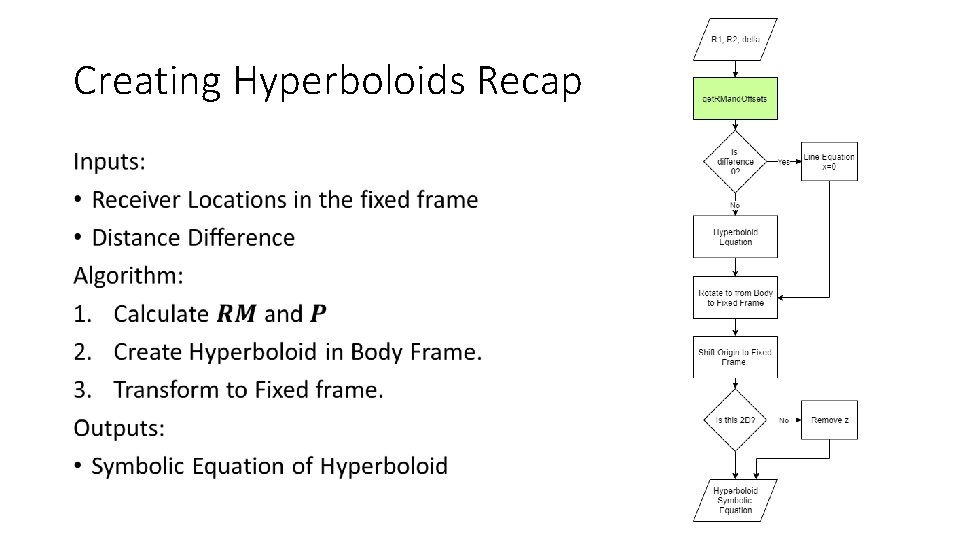
Creating Hyperboloids Recap •
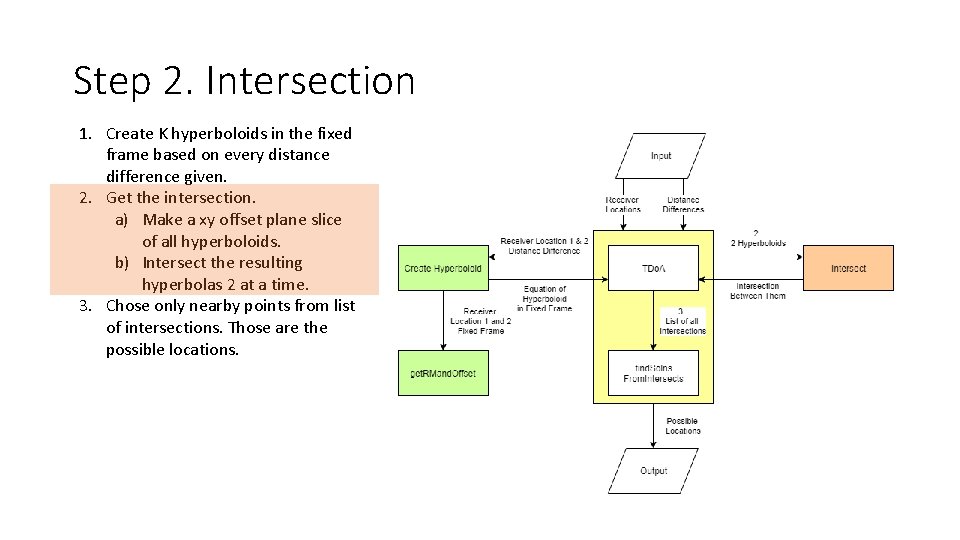
Step 2. Intersection 1. Create K hyperboloids in the fixed frame based on every distance difference given. 2. Get the intersection. a) Make a xy offset plane slice of all hyperboloids. b) Intersect the resulting hyperbolas 2 at a time. 3. Chose only nearby points from list of intersections. Those are the possible locations.

Intersecting 2 Surfaces 2 D
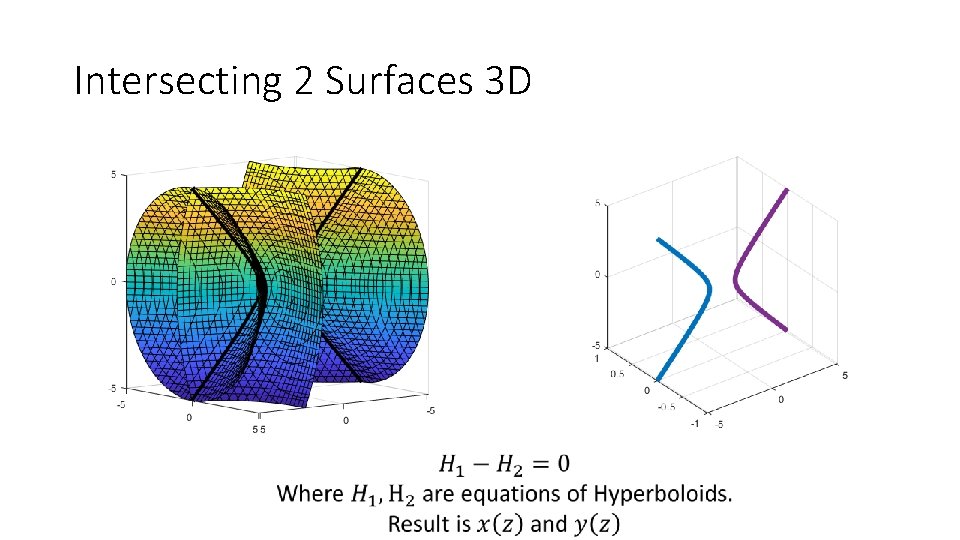
Intersecting 2 Surfaces 3 D
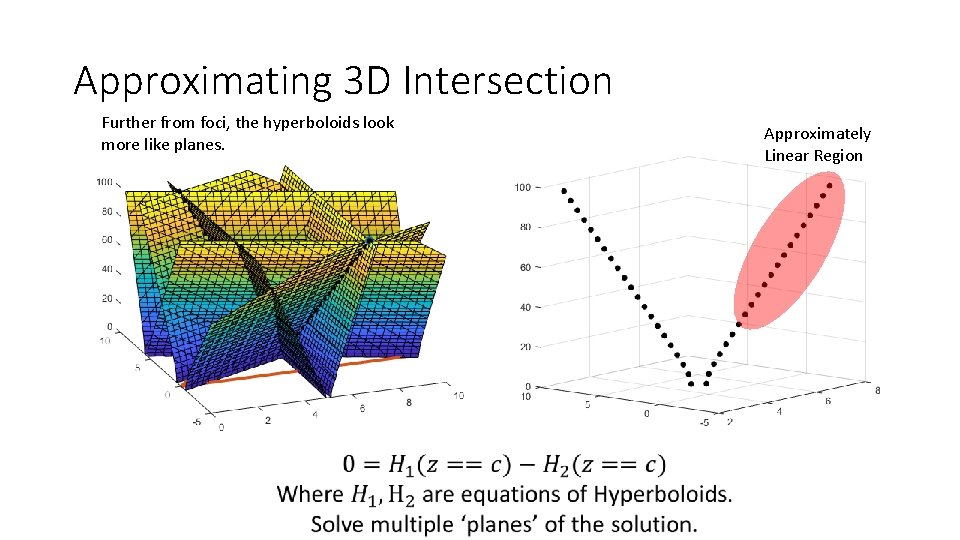
Approximating 3 D Intersection Further from foci, the hyperboloids look more like planes. Approximately Linear Region
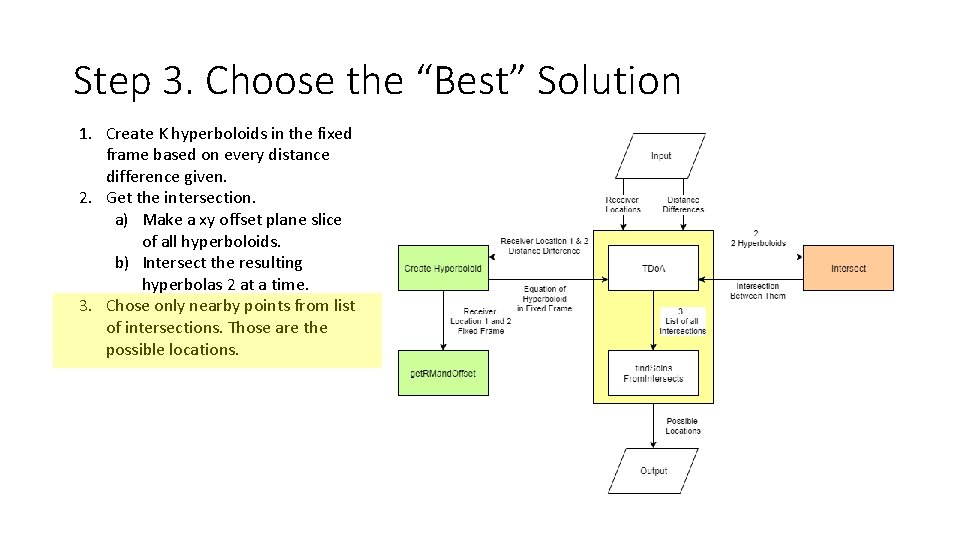
Step 3. Choose the “Best” Solution 1. Create K hyperboloids in the fixed frame based on every distance difference given. 2. Get the intersection. a) Make a xy offset plane slice of all hyperboloids. b) Intersect the resulting hyperbolas 2 at a time. 3. Chose only nearby points from list of intersections. Those are the possible locations.
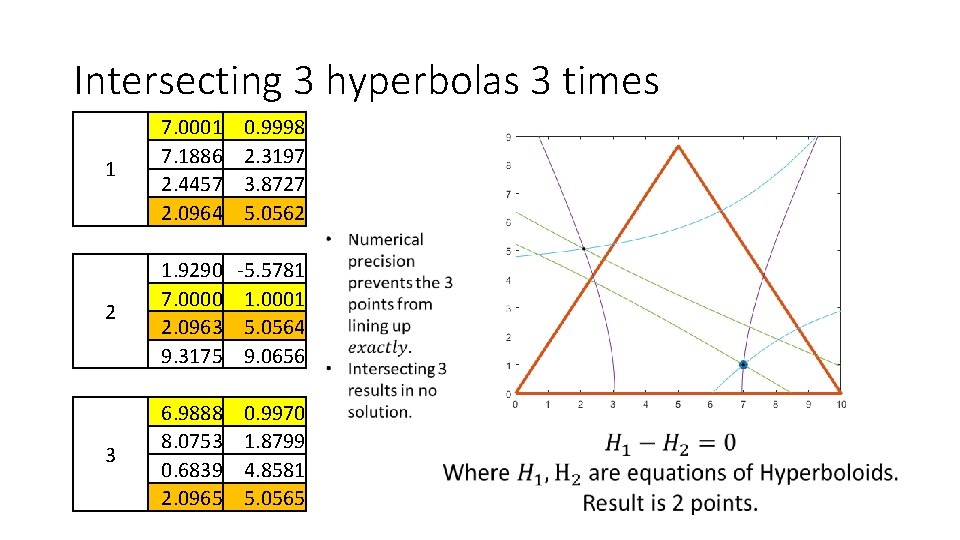
Intersecting 3 hyperbolas 3 times 1 7. 0001 7. 1886 2. 4457 2. 0964 0. 9998 2. 3197 3. 8727 5. 0562 2 1. 9290 7. 0000 2. 0963 9. 3175 -5. 5781 1. 0001 5. 0564 9. 0656 3 6. 9888 8. 0753 0. 6839 2. 0965 0. 9970 1. 8799 4. 8581 5. 0565
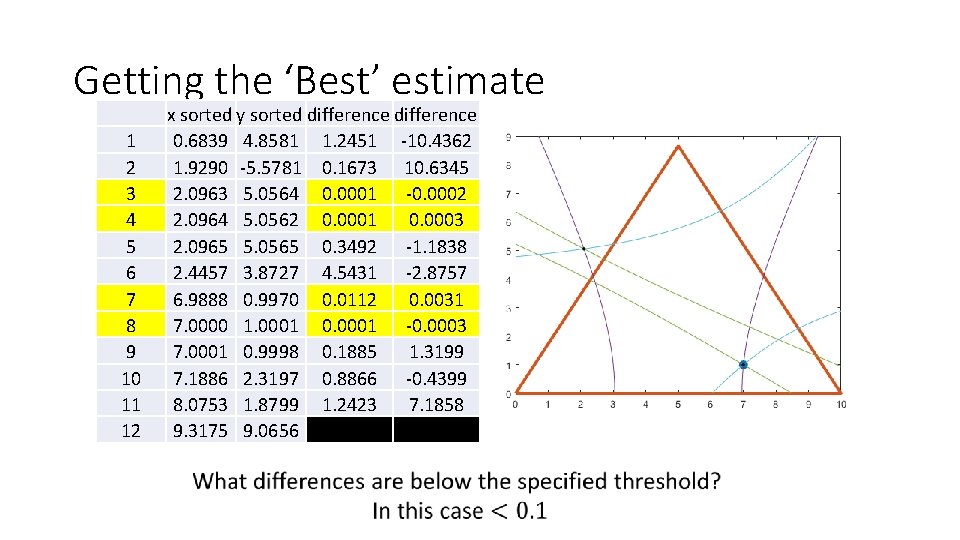
Getting the ‘Best’ estimate 1 2 3 4 5 6 7 8 9 10 11 12 x sorted y sorted difference 0. 6839 4. 8581 1. 2451 -10. 4362 1. 9290 -5. 5781 0. 1673 10. 6345 2. 0963 5. 0564 0. 0001 -0. 0002 2. 0964 5. 0562 0. 0001 0. 0003 2. 0965 5. 0565 0. 3492 -1. 1838 2. 4457 3. 8727 4. 5431 -2. 8757 6. 9888 0. 9970 0. 0112 0. 0031 7. 0000 1. 0001 0. 0001 -0. 0003 7. 0001 0. 9998 0. 1885 1. 3199 7. 1886 2. 3197 0. 8866 -0. 4399 8. 0753 1. 8799 1. 2423 7. 1858 9. 3175 9. 0656

Index 1 2 3 4 5 6 7 8 9 10 11 12 Getting the ‘Best’ estimate Diff - 1 x sorted y sorted difference 0. 6839 4. 8581 1. 2451 -10. 4362 1. 9290 -5. 5781 0. 1673 10. 6345 0 2. 0963 5. 0564 0. 0001 -0. 0002 2 2. 0964 5. 0562 0. 0001 0. 0003 2. 0965 5. 0565 0. 3492 -1. 1838 2. 4457 3. 8727 4. 5431 -2. 8757 0 6. 9888 0. 9970 0. 0112 0. 0031 7. 0000 1. 0001 0. 0001 -0. 0003 0 7. 0001 0. 9998 0. 1885 1. 3199 7. 1886 2. 3197 0. 8866 -0. 4399 8. 0753 1. 8799 1. 2423 7. 1858 9. 3175 9. 0656

Index 1 2 3 4 5 6 7 8 9 10 11 12 Getting the ‘Best’ estimate Diff - 1 x sorted y sorted difference 0. 6839 4. 8581 1. 2451 -10. 4362 1. 9290 -5. 5781 0. 1673 10. 6345 0 2. 0963 5. 0564 0. 0001 -0. 0002 2 2. 0964 5. 0562 0. 0001 0. 0003 2. 0965 5. 0565 0. 3492 -1. 1838 2. 4457 3. 8727 4. 5431 -2. 8757 0 6. 9888 0. 9970 0. 0112 0. 0031 7. 0000 1. 0001 0. 0001 -0. 0003 7. 0001 0. 9998 0. 1885 1. 3199 7. 1886 2. 3197 0. 8866 -0. 4399 8. 0753 1. 8799 1. 2423 7. 1858 9. 3175 9. 0656

Index 1 2 3 4 5 6 7 8 9 10 11 12 Getting the ‘Best’ estimate Diff - 1 x sorted y sorted difference 0. 6839 4. 8581 1. 2451 -10. 4362 1. 9290 -5. 5781 0. 1673 10. 6345 0 2. 0963 5. 0564 0. 0001 -0. 0002 2 2. 0964 5. 0562 0. 0001 0. 0003 2. 0965 5. 0565 0. 3492 -1. 1838 2. 4457 3. 8727 4. 5431 -2. 8757 0 6. 9888 0. 9970 0. 0112 0. 0031 7. 0000 1. 0001 0. 0001 -0. 0003 7. 0001 0. 9998 0. 1885 1. 3199 7. 1886 2. 3197 0. 8866 -0. 4399 8. 0753 1. 8799 1. 2423 7. 1858 9. 3175 9. 0656
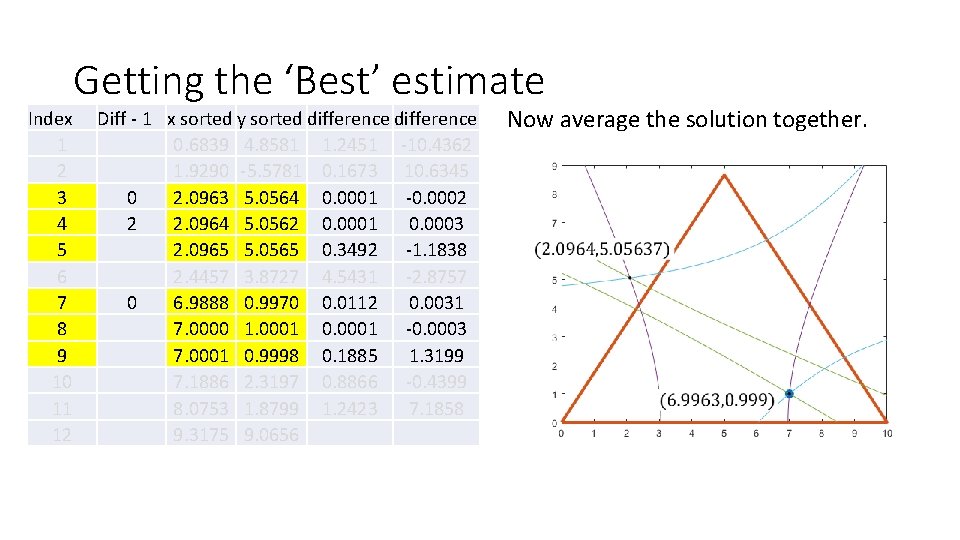
Index 1 2 3 4 5 6 7 8 9 10 11 12 Getting the ‘Best’ estimate Diff - 1 x sorted y sorted difference 0. 6839 4. 8581 1. 2451 -10. 4362 1. 9290 -5. 5781 0. 1673 10. 6345 0 2. 0963 5. 0564 0. 0001 -0. 0002 2 2. 0964 5. 0562 0. 0001 0. 0003 2. 0965 5. 0565 0. 3492 -1. 1838 2. 4457 3. 8727 4. 5431 -2. 8757 0 6. 9888 0. 9970 0. 0112 0. 0031 7. 0000 1. 0001 0. 0001 -0. 0003 7. 0001 0. 9998 0. 1885 1. 3199 7. 1886 2. 3197 0. 8866 -0. 4399 8. 0753 1. 8799 1. 2423 7. 1858 9. 3175 9. 0656 Now average the solution together.
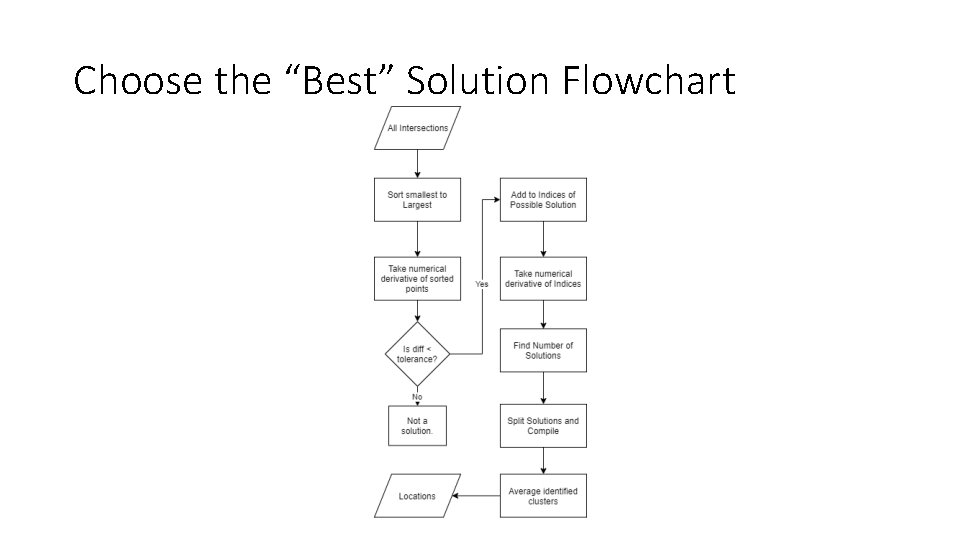
Choose the “Best” Solution Flowchart

Points on Planes to a Line Fit.

Line to Azimuth and Elevation. 1. Intersect Line and Earth Model a) Earth is sphere. b) Constitutes our “reference frame location” 2. Convert Line direction vector to Azimuth and Elevation

Real Example with Satellite • Satellite located above the Sentinel Statue with altitude 775 km • 3 Stations located at the Hill, Ellingson, and RIT Inn. Results: Line Fit via 3 points. Extra -77. 76 43. 22793 Real -77. 5685 42. 90641 Difference 0. 1914 -0. 3215
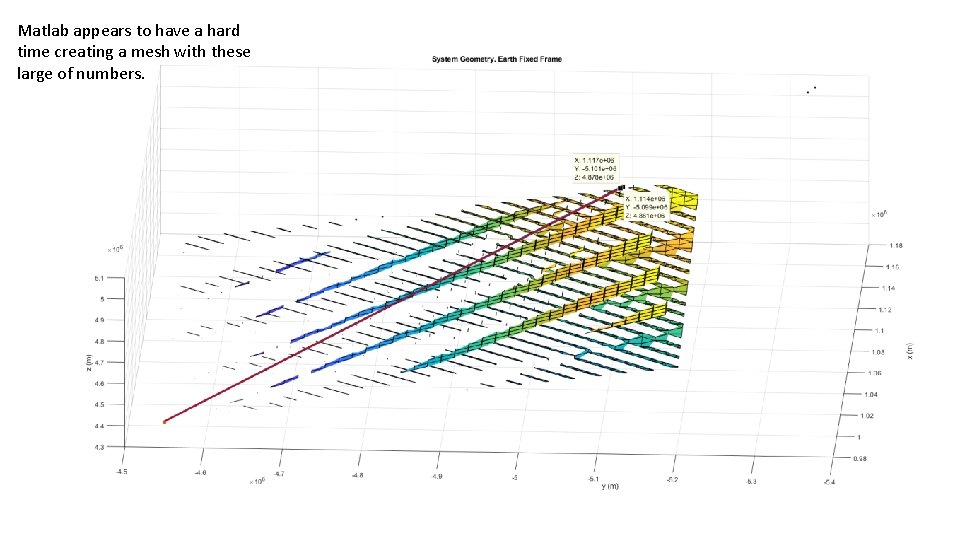
Matlab appears to have a hard time creating a mesh with these large of numbers. Real Example with Satellite

Hyperboloids look like planes out this far. Real Example with Satellite
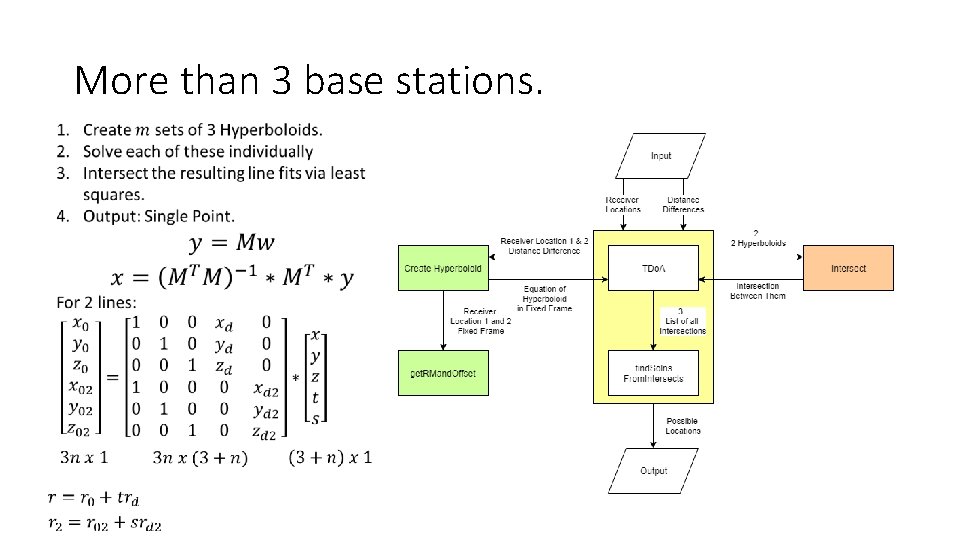
More than 3 base stations.

Preliminary Sensitivity Analysis Progress Report 10/29

More than 3 base stations with small errors. 1. Poorly Constructed problem. 2. Slopes of each line are too similar – near parallel. 3. Slight deviations result in huge errors. No error Position Err. (m) 625 0. 001% Location Err. 256, 000 2% Time Error 16, 000

3 Base Stations with small errors. • Satellite is over Sentinel still. Stations are located on Ellingson, The Hill, and RIT Inn. • Time error is 300 picoseconds Resulting Errors from Time Sync. One at a Time. Receiver A B C Error (rad)
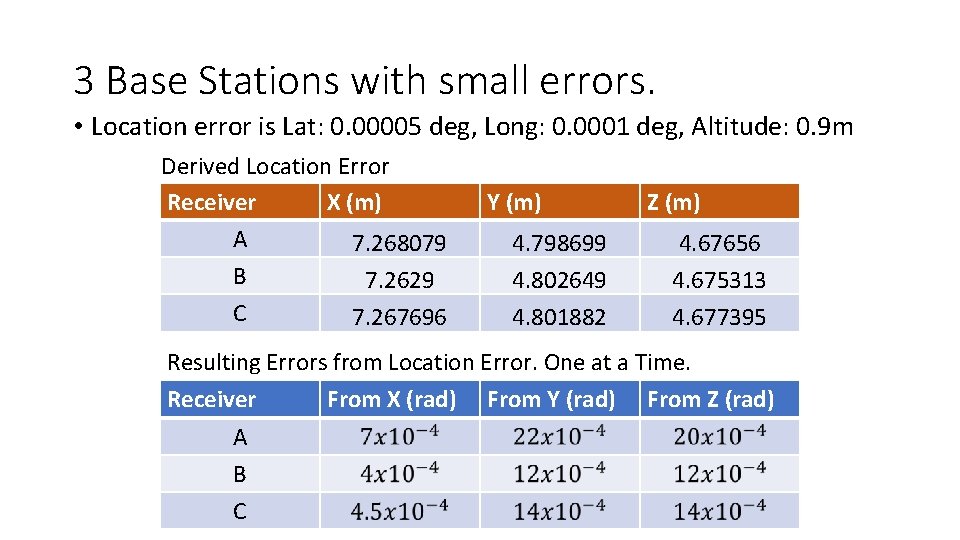
3 Base Stations with small errors. • Location error is Lat: 0. 00005 deg, Long: 0. 0001 deg, Altitude: 0. 9 m Derived Location Error Receiver X (m) A 7. 268079 B 7. 2629 C 7. 267696 Y (m) 4. 798699 4. 802649 4. 801882 Z (m) 4. 67656 4. 675313 4. 677395 Resulting Errors from Location Error. One at a Time. Receiver A B C From X (rad) From Y (rad) From Z (rad)
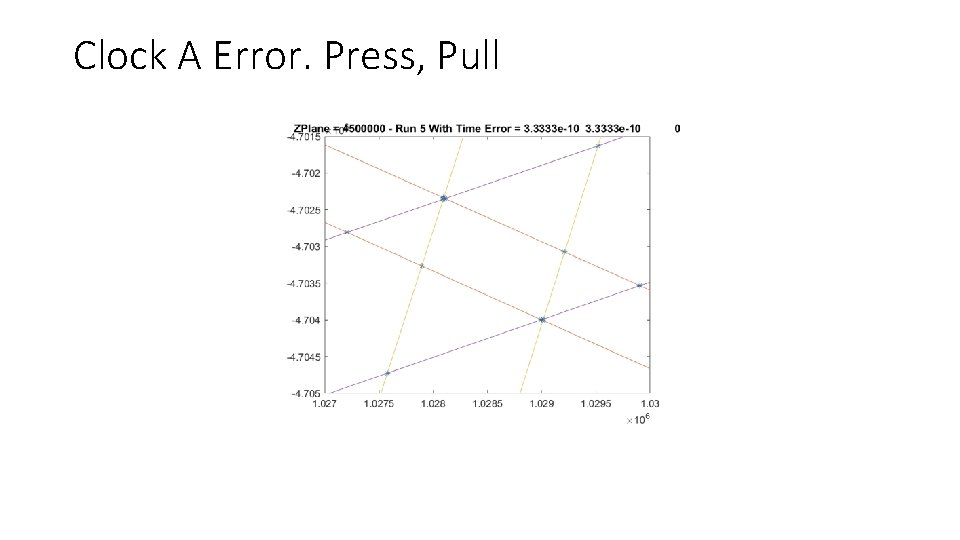
Clock A Error. Press, Pull
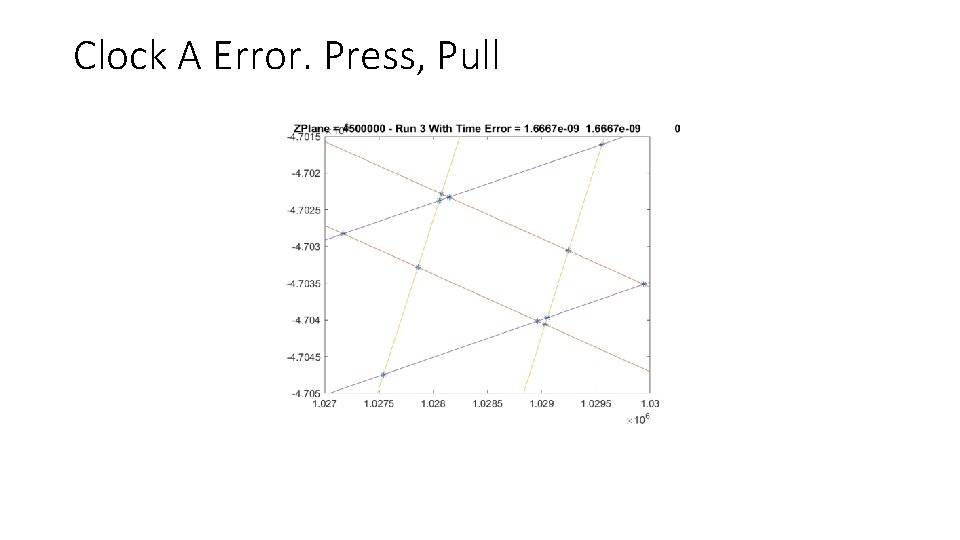
Clock A Error. Press, Pull
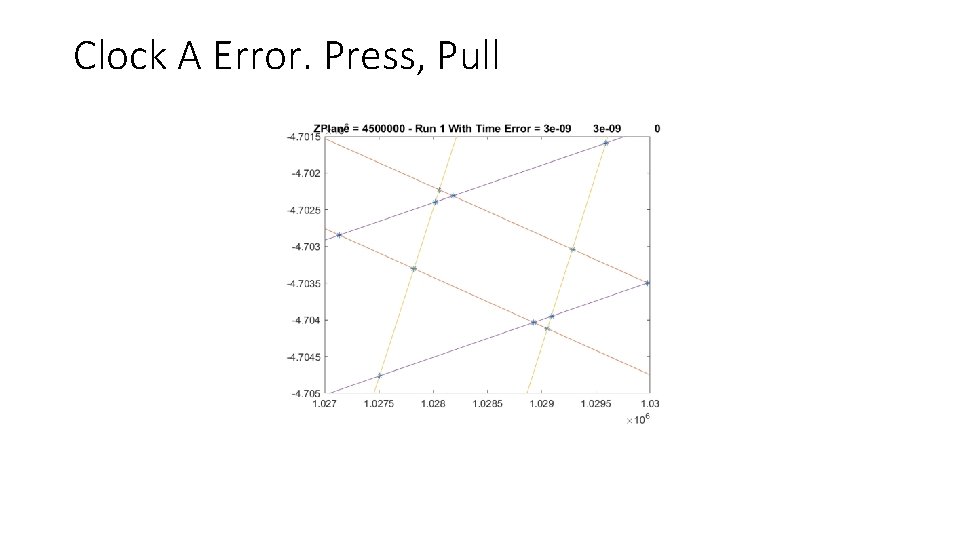
Clock A Error. Press, Pull
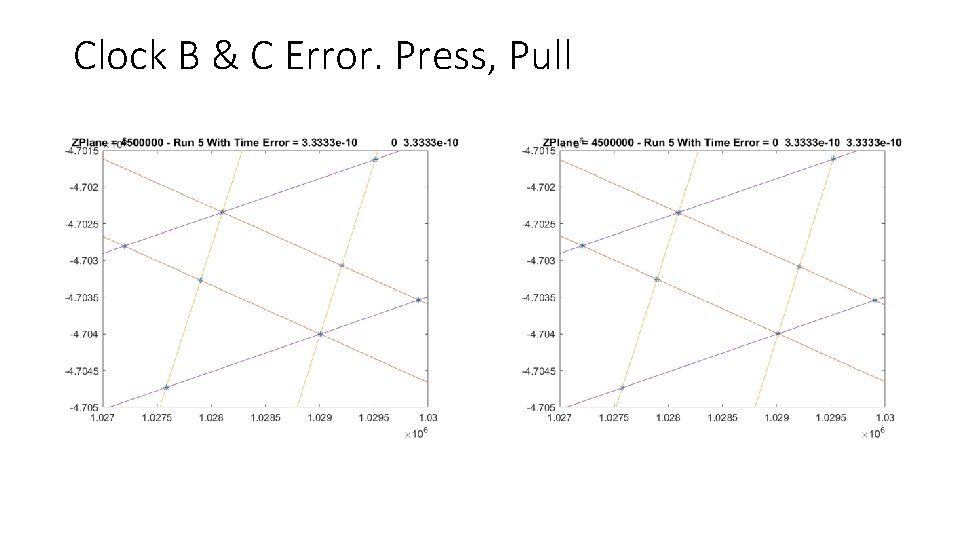
Clock B & C Error. Press, Pull
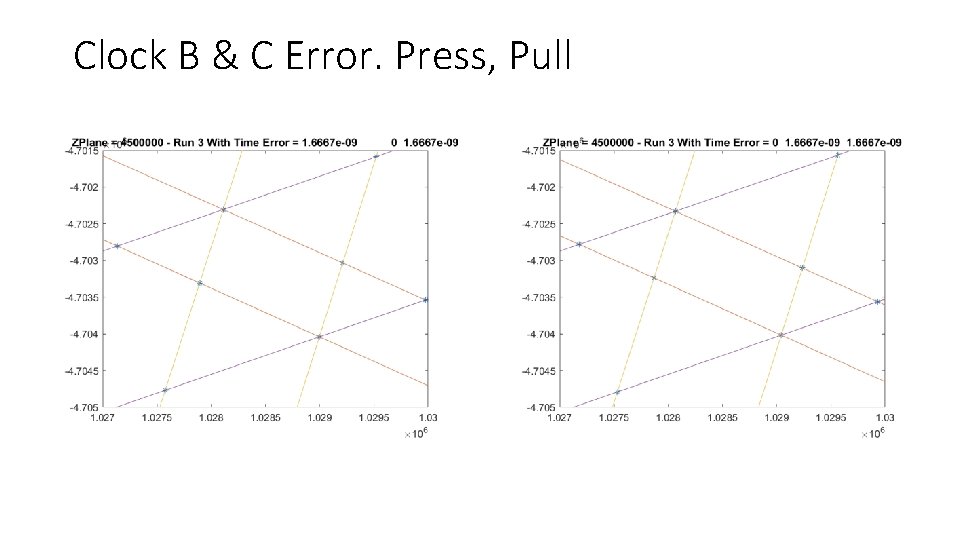
Clock B & C Error. Press, Pull
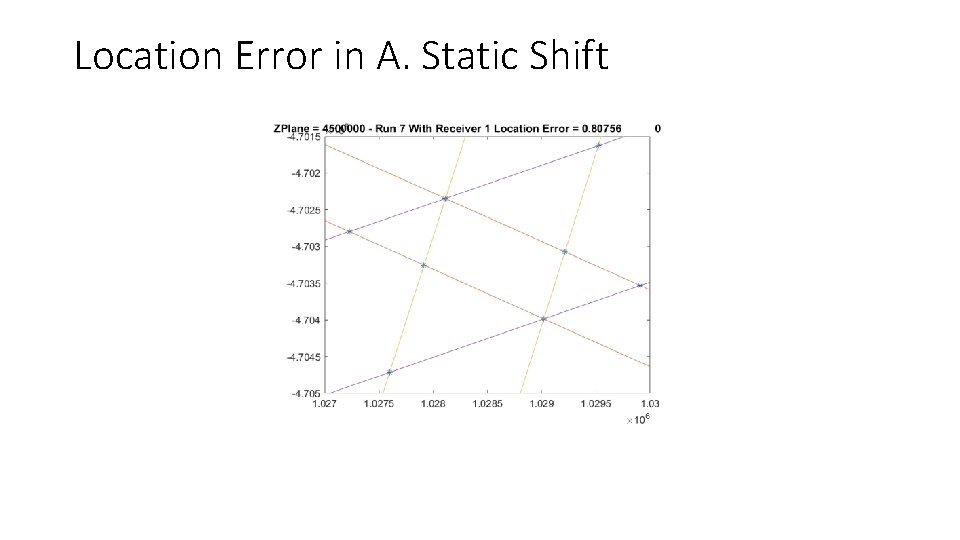
Location Error in A. Static Shift
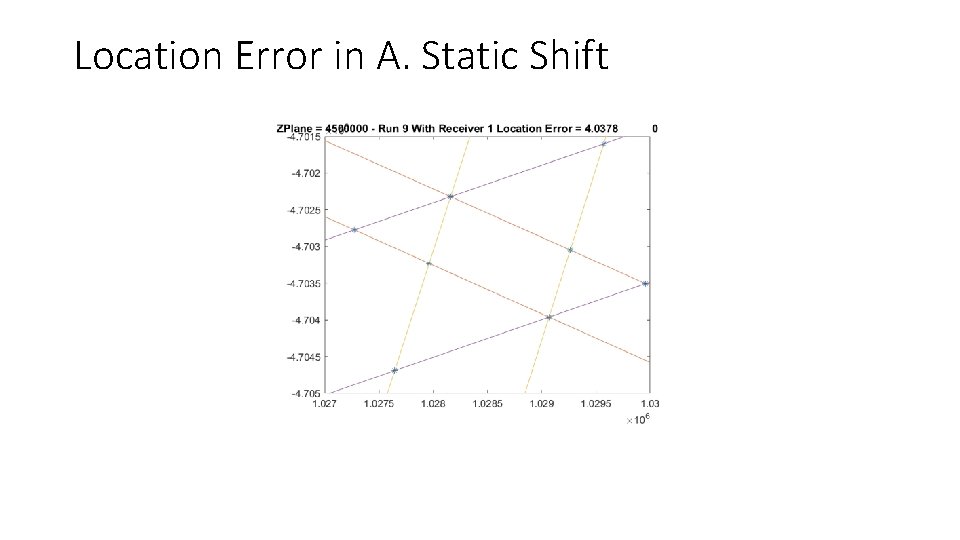
Location Error in A. Static Shift
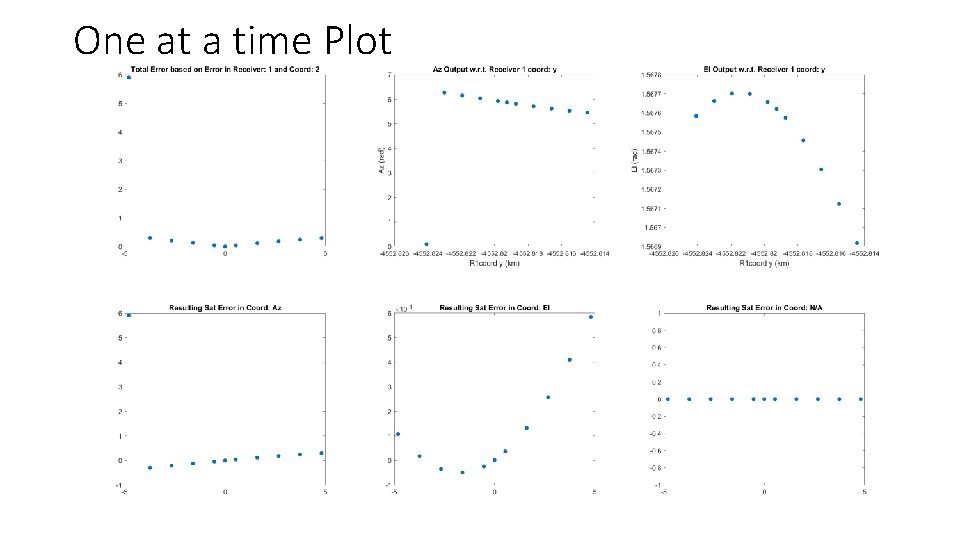
One at a time Plot
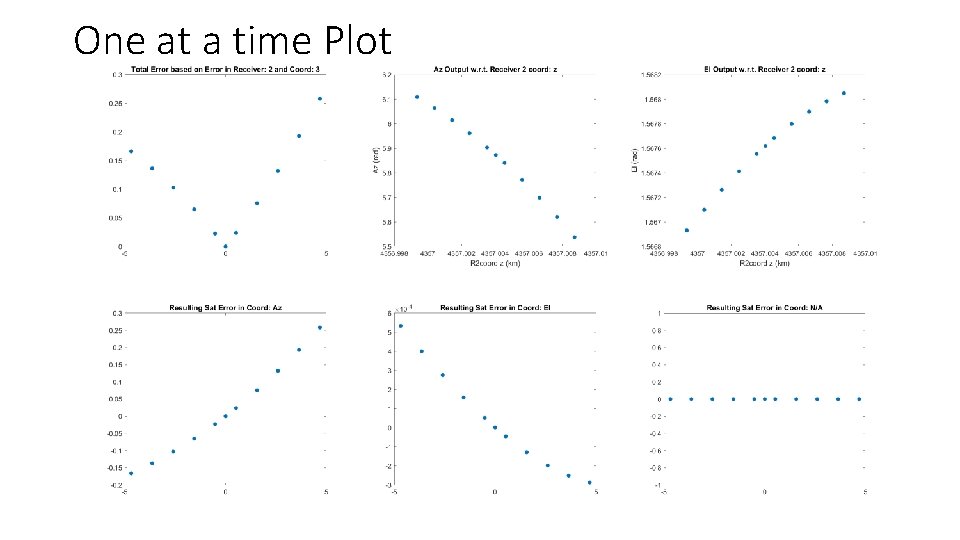
One at a time Plot
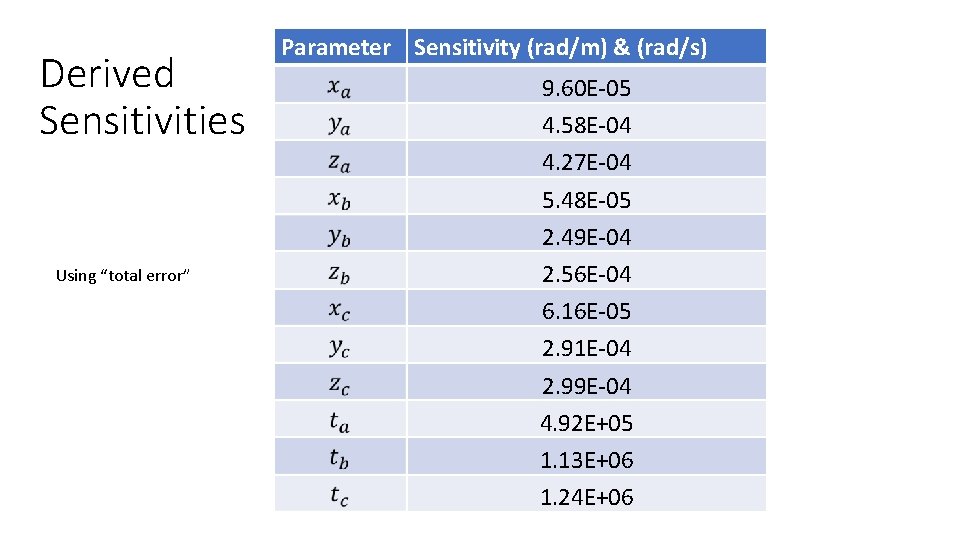
Derived Sensitivities Using “total error” Parameter Sensitivity (rad/m) & (rad/s) 9. 60 E-05 4. 58 E-04 4. 27 E-04 5. 48 E-05 2. 49 E-04 2. 56 E-04 6. 16 E-05 2. 91 E-04 2. 99 E-04 4. 92 E+05 1. 13 E+06 1. 24 E+06
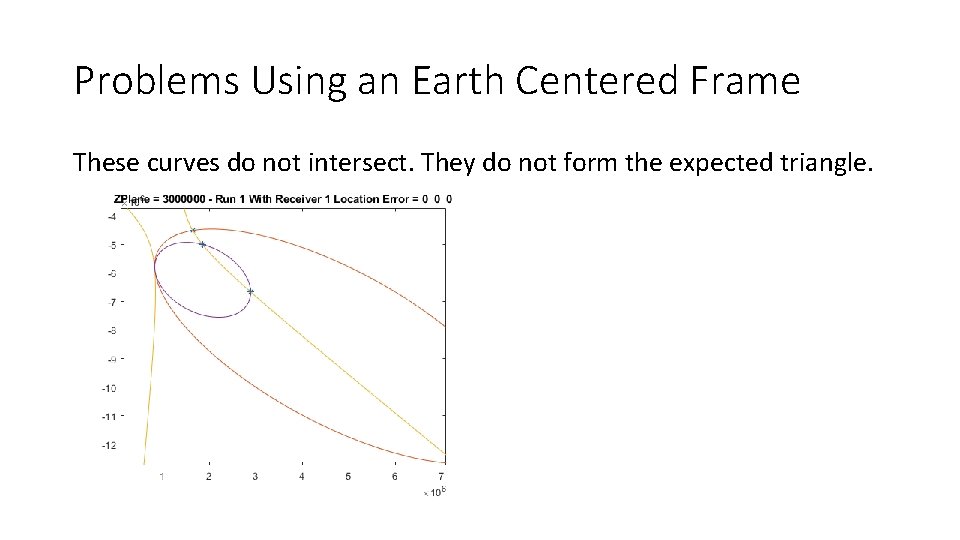
Problems Using an Earth Centered Frame These curves do not intersect. They do not form the expected triangle.
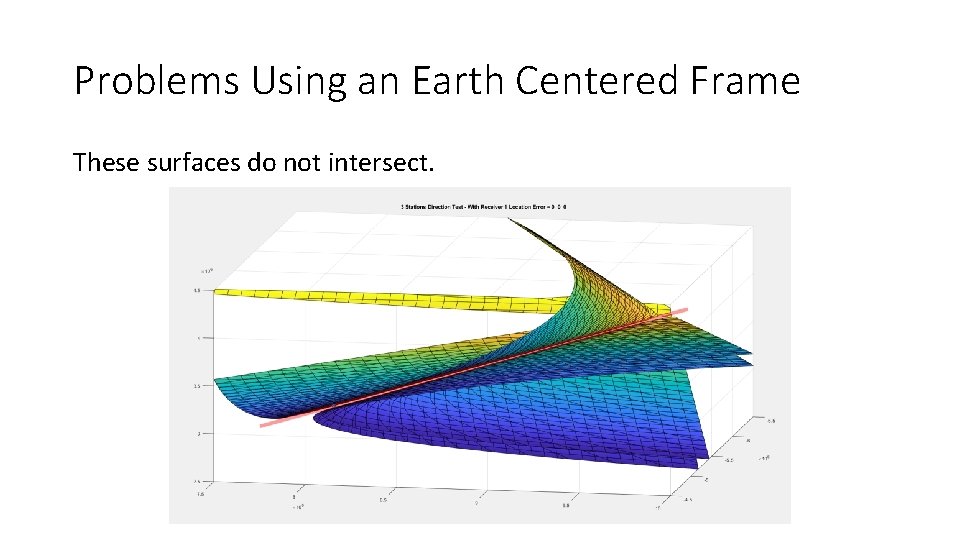
Problems Using an Earth Centered Frame These surfaces do not intersect.

Problems Using an Earth Centered Frame Are ellipses possible in 2 D slices?
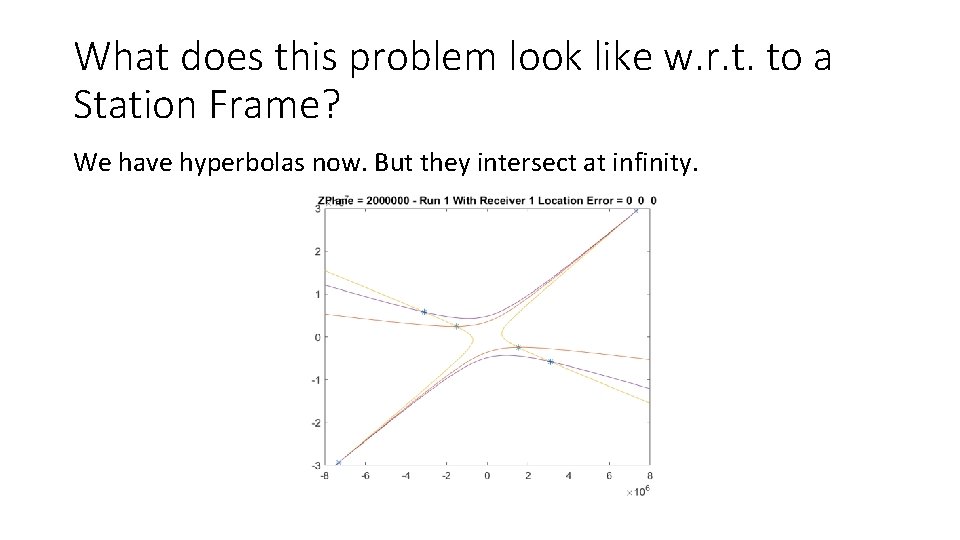
What does this problem look like w. r. t. to a Station Frame? We have hyperbolas now. But they intersect at infinity.

What does this problem look like w. r. t. to a Station Frame? Why? Poorly Constructed problem. Same input parameters, but use Receivers located at XYZ instead of Institute, Ellingson, and RIT Inn
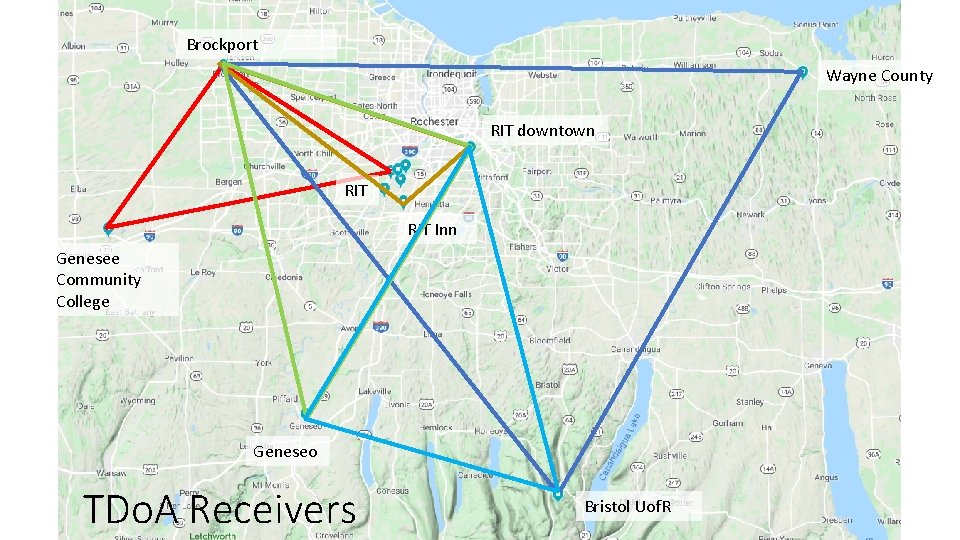
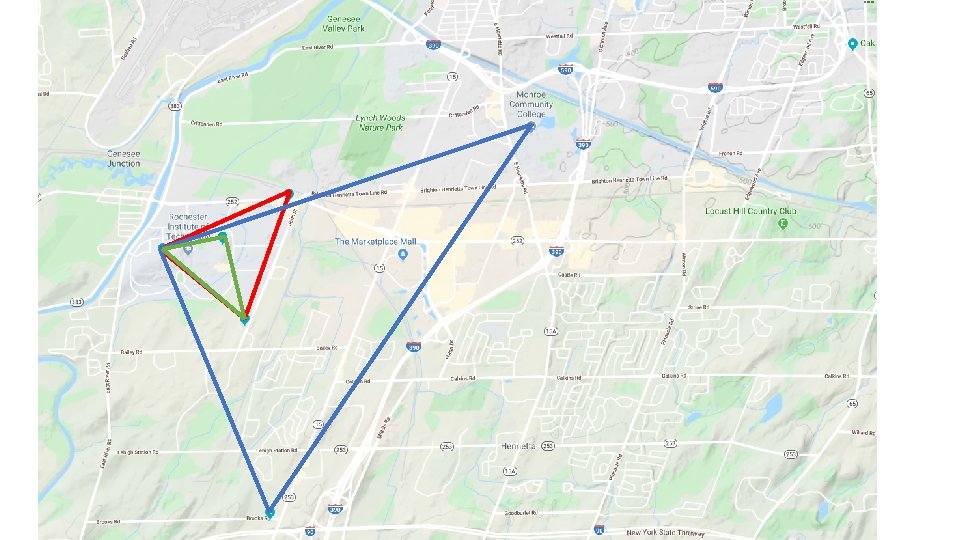
Brockport Wayne County RIT downtown RIT Inn Genesee Community College Geneseo TDo. A Receivers Bristol Uof. R

Different Models of the Earth Spherical Model Analytical (Lat, Long) -> (x, y, z) WGS 84 Model Matlab and Orekit Built-in functions available, not sure how they compute (x, y, z) http: //support. virtual-surveyor. com/en/support/solutions/articles/1000261351 -what-is-wgs 84 -

Next Steps For Thursday: • Input a ground track into the simulator. • Estimate the sensitivities at each point in the ground track Needed Inputs: • Ground Track from Orekit • Conservative uncertainties for Location Err. And Time Sync Error.

Next Steps Coming down the pipe: • Using 4 stations to yield an average direction. • Montecarlo. Allow all uncertainties to vary simultaneously • Updates to logic in TDo. A when finding points. Way in the future • Reexamine solving for a point via 4 stations. • Train a convolutional neural network to solve for the location of the satellite • (my Machine Intelligence Term project)

1 sided vs. 2 sided Hyperbolas Progress Report 11/12
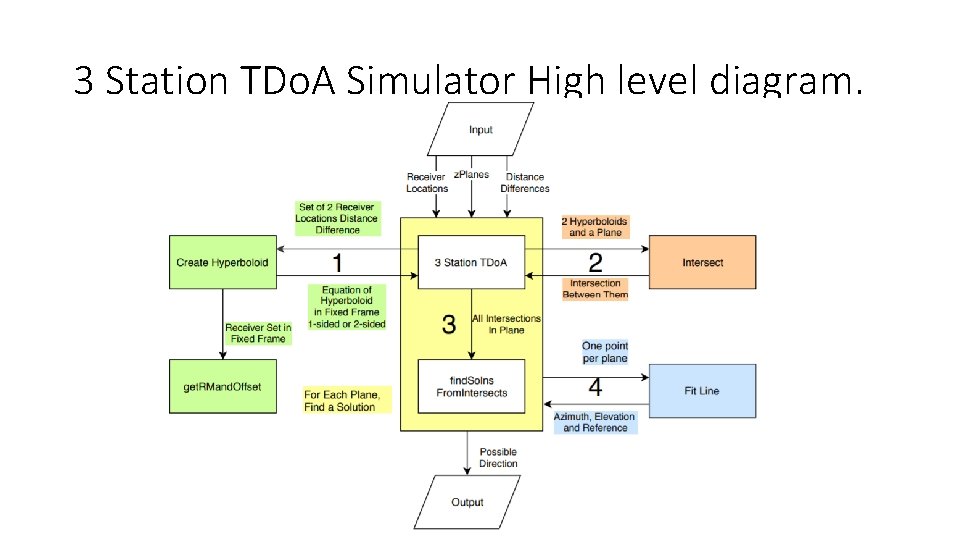
3 Station TDo. A Simulator High level diagram.

Changing to a 1 sided Hyperbola •
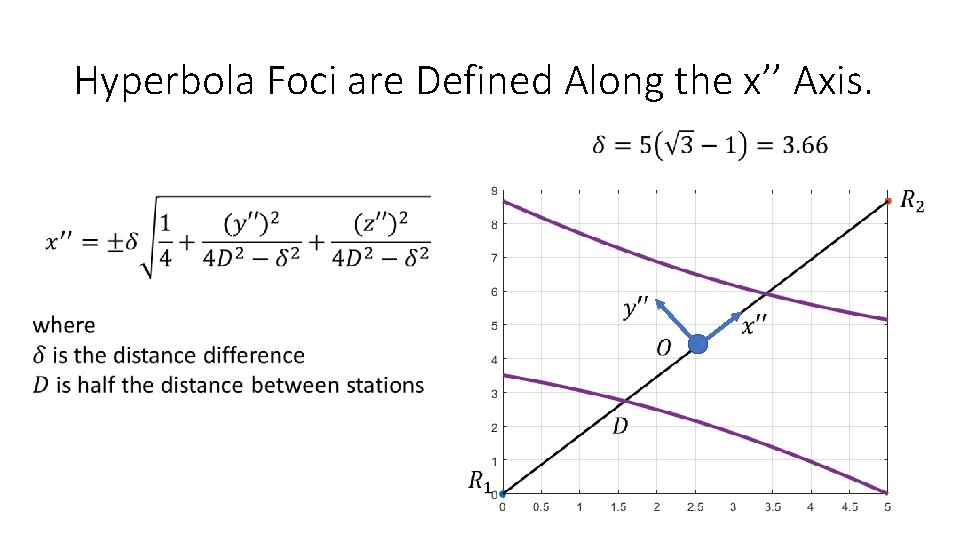
Hyperbola Foci are Defined Along the x’’ Axis.
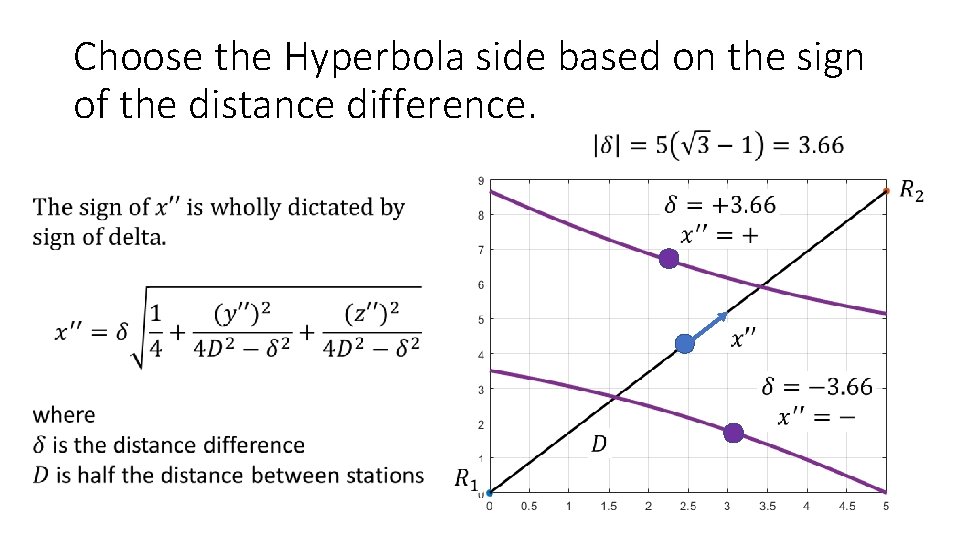
Choose the Hyperbola side based on the sign of the distance difference.
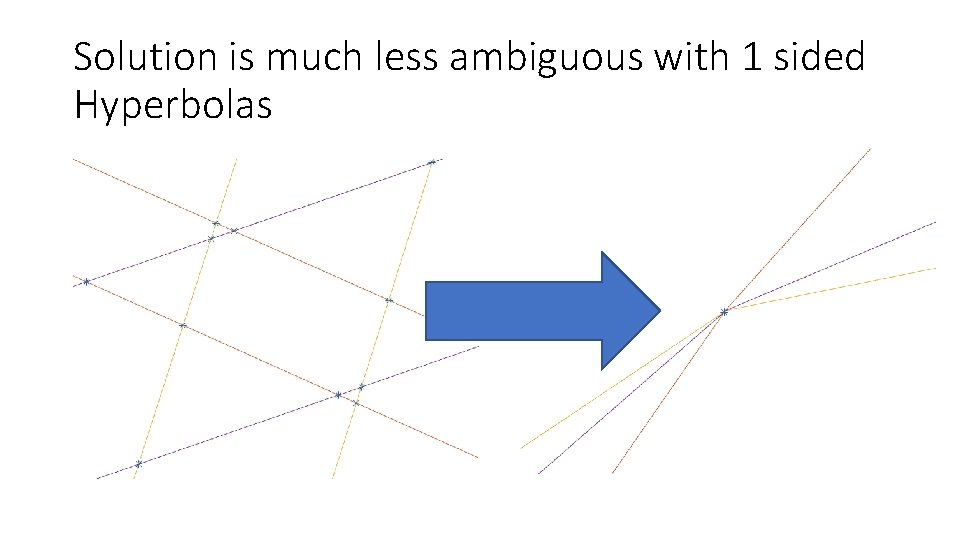
Solution is much less ambiguous with 1 sided Hyperbolas
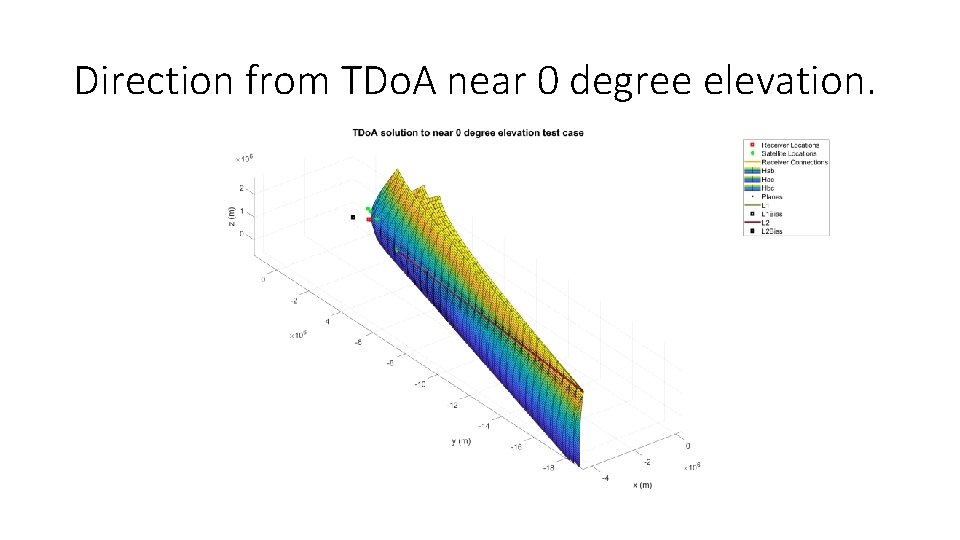
Direction from TDo. A near 0 degree elevation.
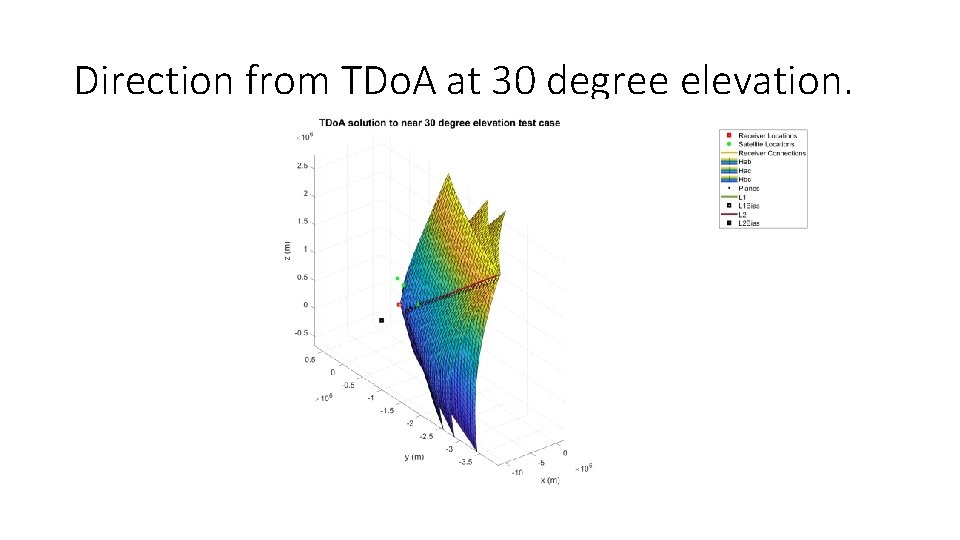
Direction from TDo. A at 30 degree elevation.

- Slides: 69