Generating Equivalent Expressions 7 EE A 1 Apply

  • Slides: 14
Download presentation
Generating Equivalent Expressions 7. EE. A. 1 Apply properties of operations as strategies to

Generating Equivalent Expressions 7. EE. A. 1 Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.

Objective: I can generate equivalent expressions.

Objective: I can generate equivalent expressions.

PART A: Let t represent the number of triangles and q represent the number

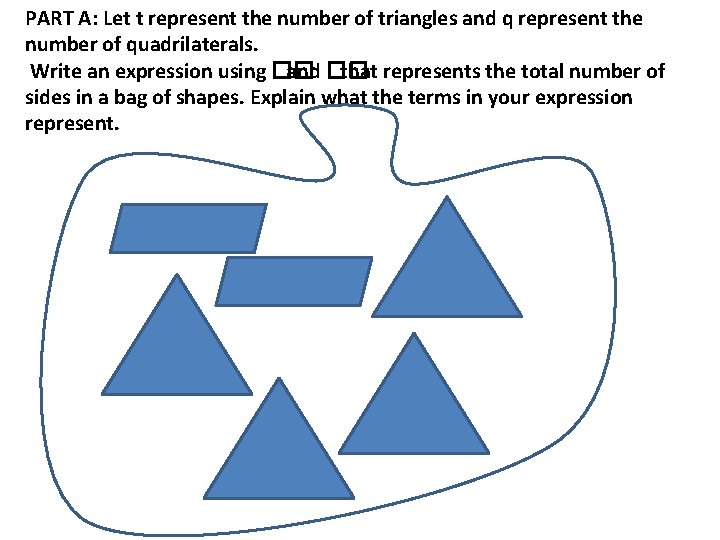
PART A: Let t represent the number of triangles and q represent the number of quadrilaterals. Write an expression using �� and �� that represents the total number of sides in a bag of shapes. Explain what the terms in your expression represent.

PART B: Mrs. Gray and Ms. King has the same number of triangles and

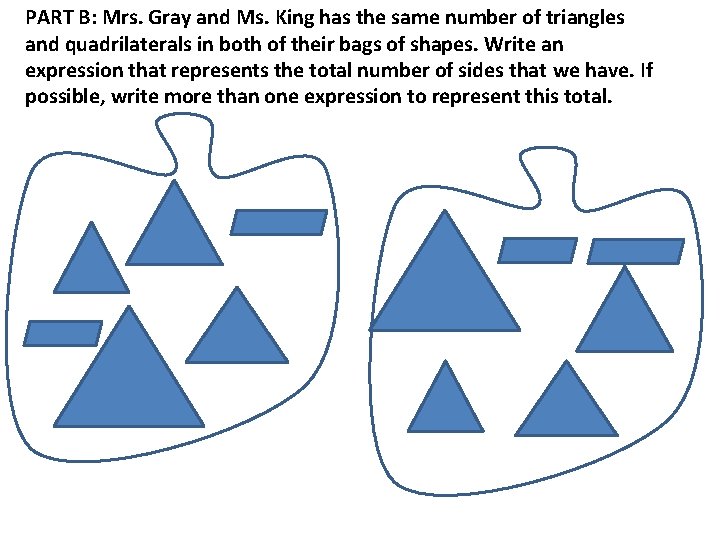
PART B: Mrs. Gray and Ms. King has the same number of triangles and quadrilaterals in both of their bags of shapes. Write an expression that represents the total number of sides that we have. If possible, write more than one expression to represent this total.

PART C: Each student in this class has a bag of shapes. Write an

PART C: Each student in this class has a bag of shapes. Write an expression that represents the total number of sides that are in every students bag of shapes in the room.

How many triangles and quadrilaterals are in one bag of shapes?

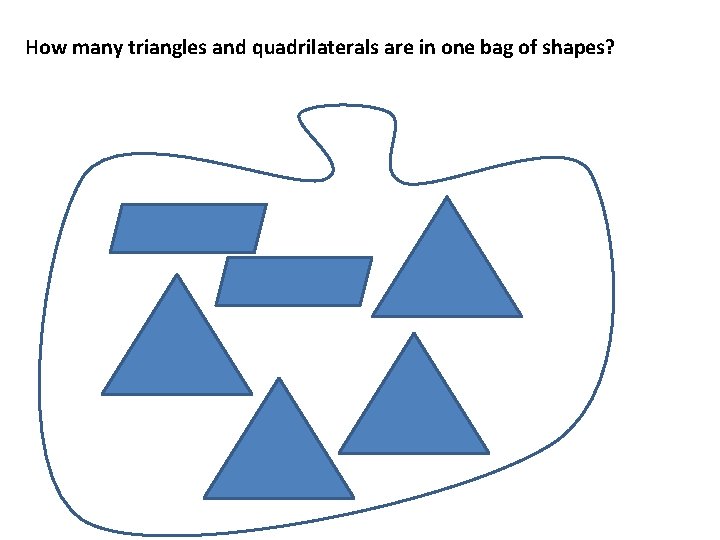
How many triangles and quadrilaterals are in one bag of shapes?

PART D: Use the given values of �� and your expression from part A

PART D: Use the given values of �� and your expression from part A to determine the number of sides that should be found in your bag. PART E: Use the same values for �� and your expression from part B to determine the number of sides that should be contained in your bag and one of your classmates bag combined. PART F: Use the same values for �� and your expression from part C to determine the number of sides that should be contained in all of the bags in the classroom combined. PART G: What do you notice about the various expressions in parts E and F?

Example 1: Any Order, Any Grouping Property with Addition a. Rewrite ���� + ����

Example 1: Any Order, Any Grouping Property with Addition a. Rewrite ���� + ���� and ���� −���� by combining like terms. Write the original expressions and expand each term using addition. What are the new expressions equivalent to?

Example 1: Any Order, Any Grouping Property with Addition b. Find the sum of

Example 1: Any Order, Any Grouping Property with Addition b. Find the sum of ���� + �� and ����.

Example 1: Any Order, Any Grouping Property with Addition c. Find the sum of

Example 1: Any Order, Any Grouping Property with Addition c. Find the sum of −���� + �� and ���� −��.

Example 2: Any Order, Any Grouping with Multiplication Find the product of ���� and

Example 2: Any Order, Any Grouping with Multiplication Find the product of ���� and ��.

Example 3: Any Order, Any Grouping in Expressions with Addition and Multiplication a. ��

Example 3: Any Order, Any Grouping in Expressions with Addition and Multiplication a. �� (���� ) b. �� y(�� ) c. �� ∙�� d. �� (2�� ) + �� y(�� ) e. �� (���� ) + �� y(�� ) + �� ∙�� f. Alexander says that ���� + �� y is equivalent to (�� ) + �� y because of any order, any grouping. Is he correct? Why or why not?

PRACTICE MAKES PERFECT

PRACTICE MAKES PERFECT

EXIT TICKET 1. Write an equivalent expression to 2�� + 3+5�� + 6 by

EXIT TICKET 1. Write an equivalent expression to 2�� + 3+5�� + 6 by combining like terms. 2. Find the sum of (8�� + 2�� − 4) and (3�� − 5). 3. Write the expression in standard form: 4(2�� ) + 7(− 4�� ) + (3 ∙ �� ∙ 5)