Generating and harnessing photonic entanglement Quantum Technology Lab

Generating and harnessing photonic entanglement Quantum Technology Lab Rohan Dalton Michael Harvey Nathan Langford Till Weinhold Jeremy O’Brien Geoff Pryde Andrew White Theory Colleagues Funding: Stephen Bartlett Aggie Branczyk Michael Bremner Jen Dodd Andrew Doherty Alexei Gilchrist Gerard Milburn Michael Nielsen Tim Ralph www. quantinfo. org Geoff Pryde

Agatha Brancyzk Rohan Dalton Stephen Bartlett Alexei Gilchrist Andrew White Nathan Langford Michael Harvey Till Weinhold Jeremy O’Brien Geoff Pryde www. quantinfo. org Gerard Milburn Tim Ralph


Generating and harnessing photonic entanglement Talk outline 1. Qubits • CNOT gate • Quantum process tomography • Generalized quantum measurements with photons 2. Qutrits and Qudits • Gaussian spatial modes • Constructing and measuring qutrits • Use in quantum bit commitment www. quantinfo. org
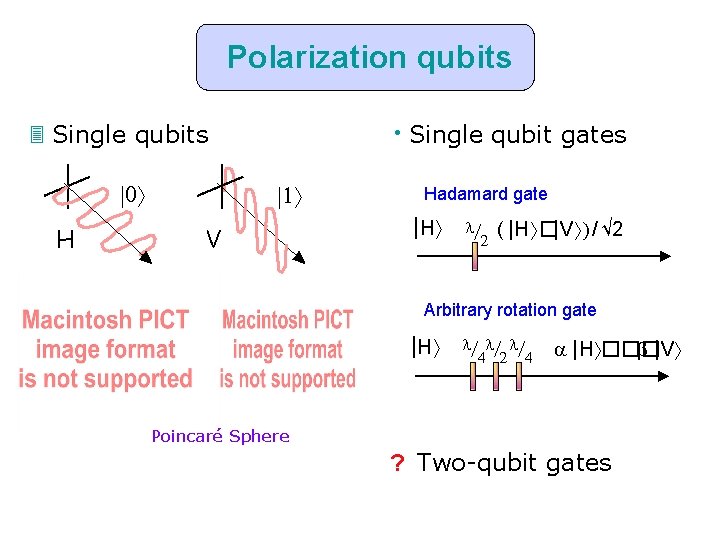
Polarization qubits 3 • Single qubit gates 3 Single qubits |0 H |1 V Hadamard gate | H / 2 ( |H � |V ) / √ 2 Arbitrary rotation gate | H / / / 2 |H ��� |V Poincaré Sphere ? Two-qubit gates
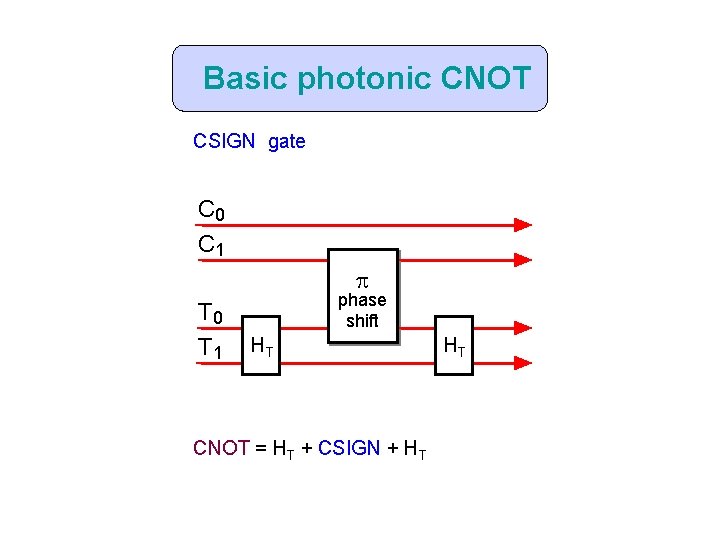
Basic photonic CNOT CSIGN gate C 0 C 1 p T 0 T 1 phase shift HT CNOT = HT + CSIGN + HT HT

2 -photon CNOT operation CSIGN gate -1/ 3 Ralph, Langford, Bell & White, PRA 65, 062324 (2002) Hofmann & Takeuchi, PRA 66, 024308 (2002)

2 -photon CNOT operation CSIGN gate -1/ 3 both reflected transmitted Ralph, Langford, Bell & White, PRA 65, 062324 (2002) Hofmann & Takeuchi, PRA 66, 024308 (2002)

2 -photon CNOT operation CSIGN gate -1/ 3 Ralph, Langford, Bell & White, PRA 65, 062324 (2002) Hofmann & Takeuchi, PRA 66, 024308 (2002)

Polarization 2 -photon CNOT gate -1/ 3 Control out Control in 1/ 3 Target out Target in 1/ 3 Ralph, Langford, Bell & White, PRA 65, 062324 (2002) Hofmann & Takeuchi, PRA 66, 024308 (2002)
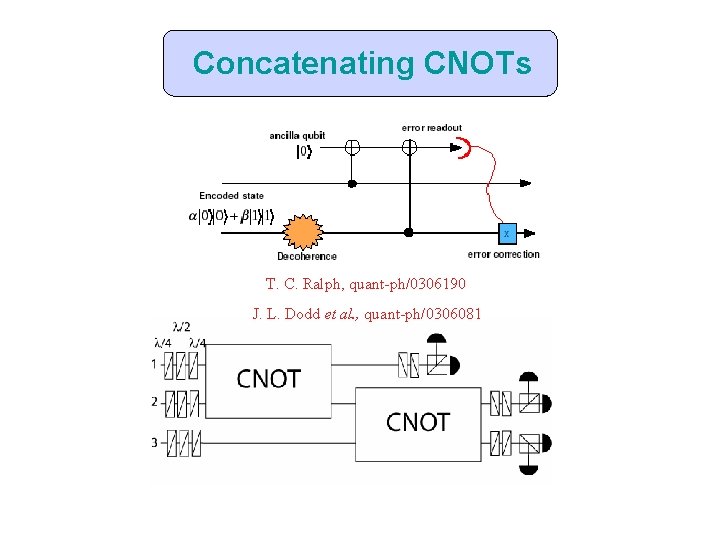
Concatenating CNOTs T. C. Ralph, quant-ph/0306190 J. L. Dodd et al. , quant-ph/0306081

2 -photon CNOT in the context of scalable QC LOQC = “Linear Optics Quantum Computing” Knill, Laflamme and Milburn, Nature 409, 46 (2001)

2 -photon CNOT circuit Non-classical interference Very stable: insensitive to x-y-z translation J. L. O’Brien, G. J. Pryde, et al. , Nature 426, 264 (2003)
![Truth table Ideal Measured Average logical fidelity = Tr [Mideal Mmeas]/4 = 94 ± Truth table Ideal Measured Average logical fidelity = Tr [Mideal Mmeas]/4 = 94 ±](http://slidetodoc.com/presentation_image_h/321f19867e12d76bfdbee4de23822967/image-14.jpg)
Truth table Ideal Measured Average logical fidelity = Tr [Mideal Mmeas]/4 = 94 ± 2 % O’Brien, Pryde, et al. , Nature 426, 264 (2003) O’Brien, Pryde, et al. , PRL 93, 080502 (2004)
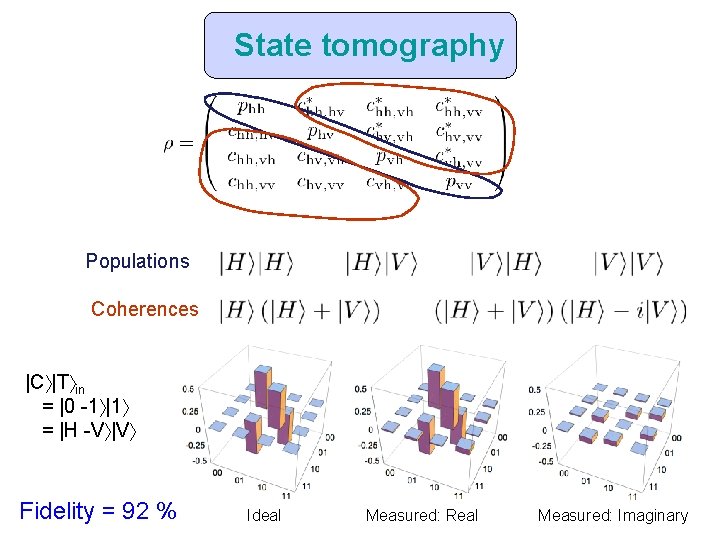
State tomography Populations Coherences |C |T in = |0 -1 |1 = |H -V |V Fidelity = 92 % Ideal Measured: Real Measured: Imaginary
Characterizing the gate itself ? Decompose into “basis” operations, e. g. rotations

Quantum process tomography Any physical process can be written as a completely positive map: For a CNOT: +0. 34 Ideal Measured (Re)
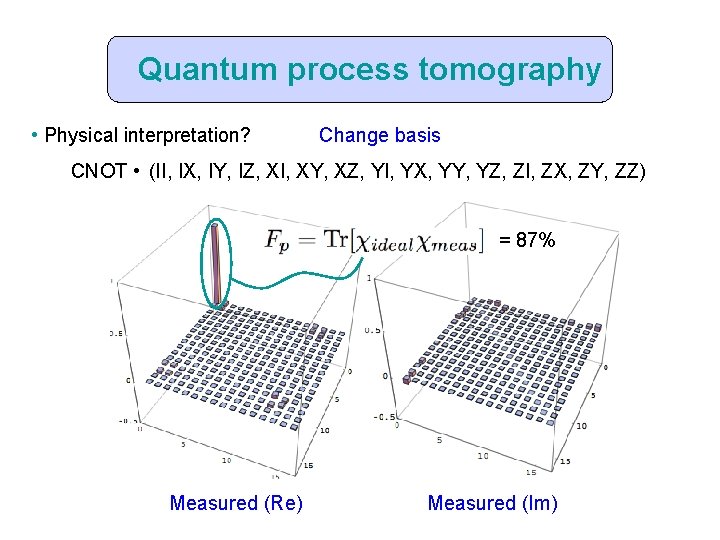
Quantum process tomography • Physical interpretation? Change basis CNOT • (II, IX, IY, IZ, XI, XY, XZ, YI, YX, YY, YZ, ZI, ZX, ZY, ZZ) = 87% Measured (Re) Measured (Im)

Gate measures • Direct measurement of process fidelity 71 measurements 93 ± 1% 95 ± 1% • Average gate fidelity where d is the Hilbert space dimension • Average error rate ≤ C 2 = 1 -Fp where C is process “closeness” 7 ± 1% • Chief source of non-ideal gate operation Gilchrist, Langford, and Nielsen, quant-ph/0408063 O’Brien, Pryde, et al. , PRL 93, 080502 (2004)

QND and Generalized Measurement 1. Measurement outcome is correlated with the signal input 2. The measurement does not alter the value of the measured obsevable 3. Repeated measurement yields the same result - quantum state preparation (QSP) Grangier et al. Nature 396, 537
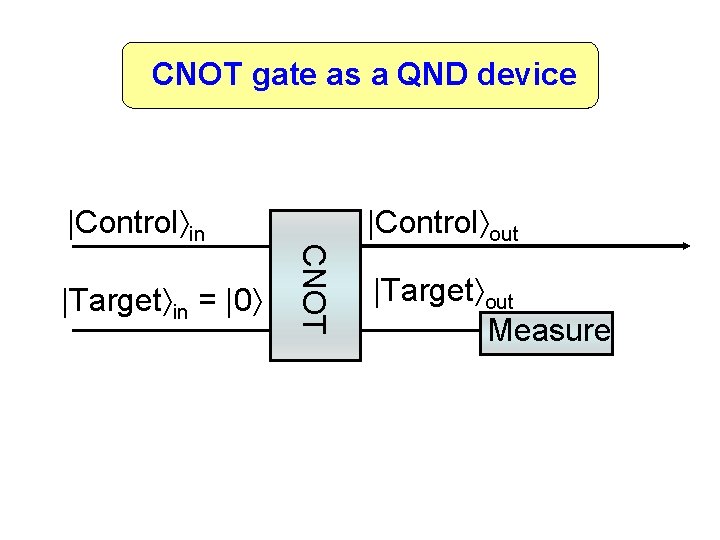
CNOT gate as a QND device |Target in = |0 CNOT |Control in |Control out |Target out Measure
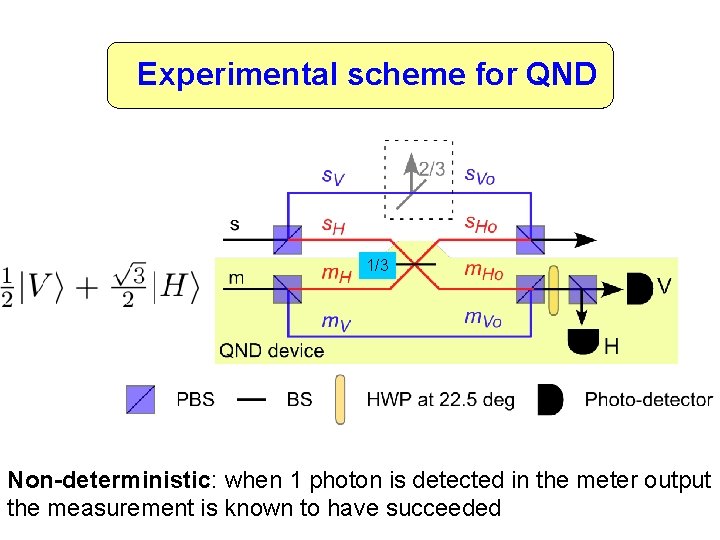
Experimental scheme for QND 1/3 Non-deterministic: when 1 photon is detected in the meter output the measurement is known to have succeeded
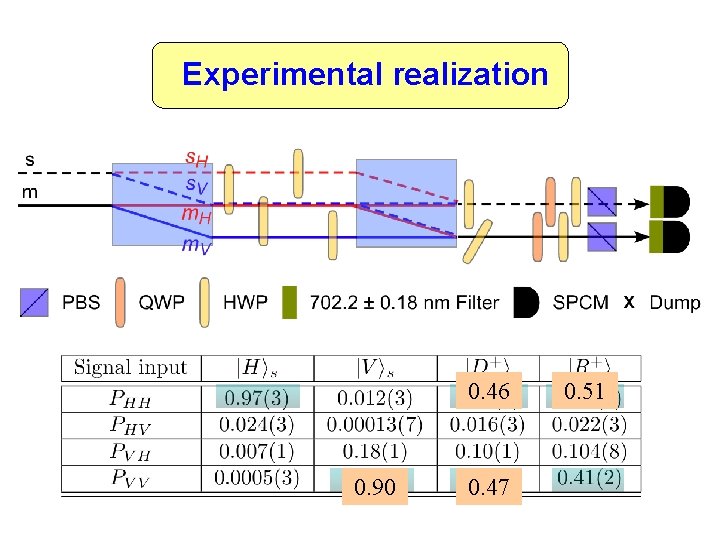
Experimental realization 0. 46 0. 90 0. 47 0. 51
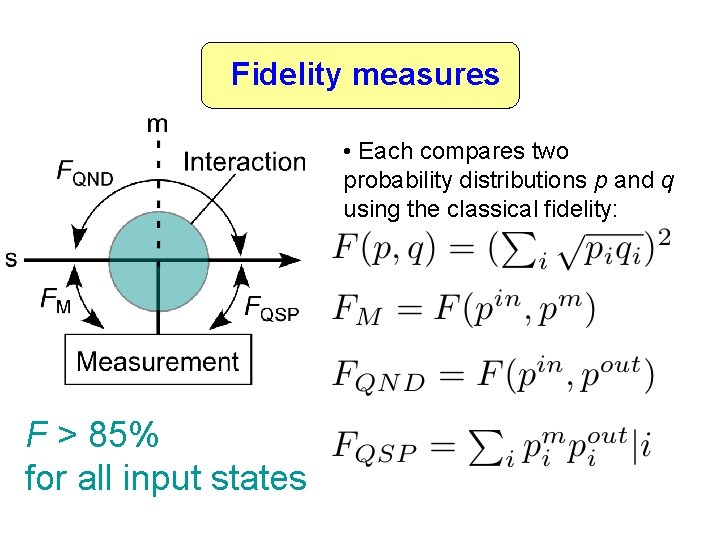
Fidelity measures • Each compares two probability distributions p and q using the classical fidelity: F > 85% for all input states
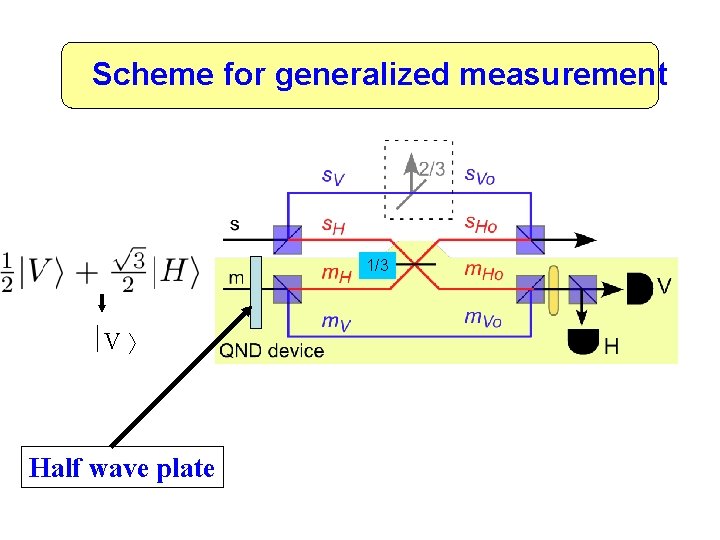
Scheme for generalized measurement 1/3 V Half wave plate

Complementarity Most advanced general measurement of a qubit: non-destructive; arbitrary strength; any basis; BUT non-deterministic Pryde, O’Brien, White, Bartlett & Ralph PRL 92, 190402 (2004)

Z-measurement error correction a (|HH> + |VV>) + b |VH> + |HV>) “V” a |V> + b |H> Teleported gates fail by making a Z-measurement LOQC cluster states Syndrome measured Knill, La. Flamme and Milburn, but not Nature 409, 46 (2001) corrected Pittman, Jacobs and Franson, Average PRA, 64, 062311 (2001) Fidelity 96 ± 3 PRL, % 93, 040503 (04) Nielsen, Browne O’Brien, Pryde& Rudolph, quant-ph/0405157 White and Ralph, quant-ph/0408064

QUTRITS

Encoding information in single photons Polarisation qubits: What if we want to create photonic qudits? Gaussian spatial modes: • Infinite dimensional • Discrete • Orthogonal • Can describe any paraxial beam
Gaussian spatial modes Gaussian optical mode: What about other spot shapes? … for paraxial beams
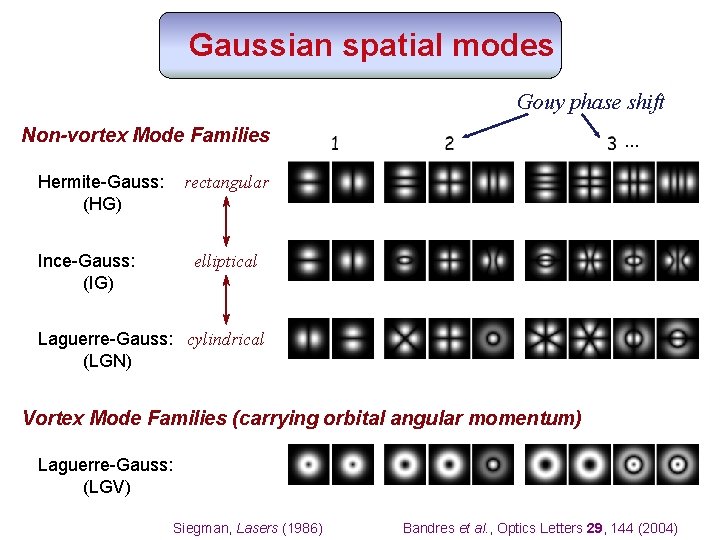
Gaussian spatial modes Gouy phase shift … Non-vortex Mode Families Hermite-Gauss: (HG) rectangular Ince-Gauss: (IG) elliptical Laguerre-Gauss: cylindrical (LGN) Vortex Mode Families (carrying orbital angular momentum) Laguerre-Gauss: (LGV) Siegman, Lasers (1986) Bandres et al. , Optics Letters 29, 144 (2004)
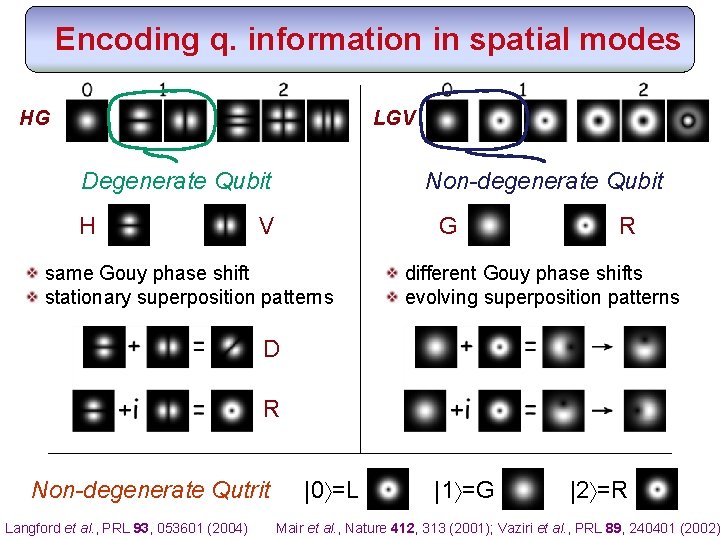
Encoding q. information in spatial modes HG LGV Degenerate Qubit H Non-degenerate Qubit V G same Gouy phase shift stationary superposition patterns R different Gouy phase shifts evolving superposition patterns D R Non-degenerate Qutrit |0 =L |1 =G |2 =R Langford et al. , PRL 93, 053601 (2004) Mair et al. , Nature 412, 313 (2001); Vaziri et al. , PRL 89, 240401 (2002)
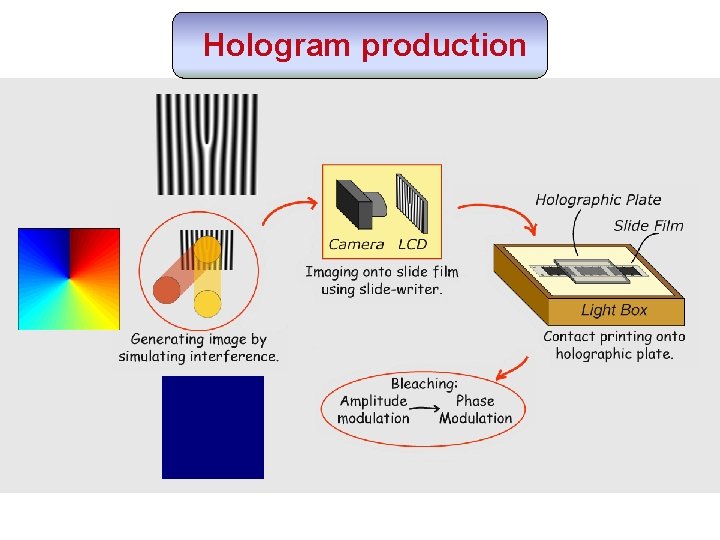
Hologram production
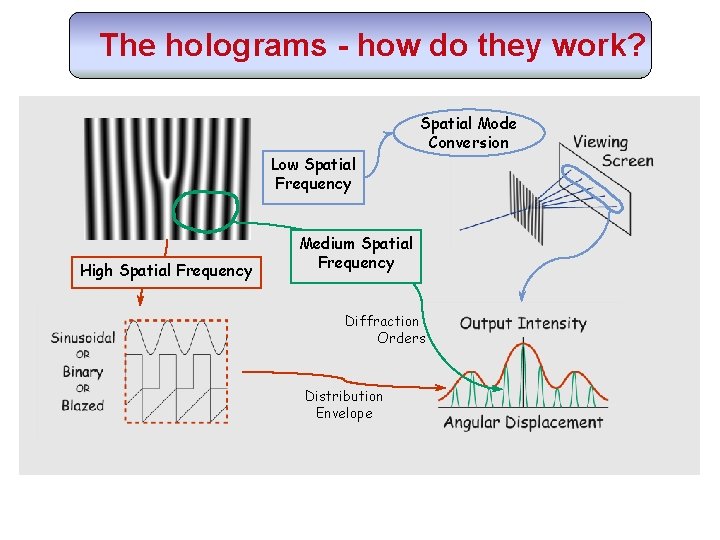
The holograms - how do they work? Low Spatial Frequency High Spatial Frequency Spatial Mode Conversion Medium Spatial Frequency Diffraction Orders Distribution Envelope
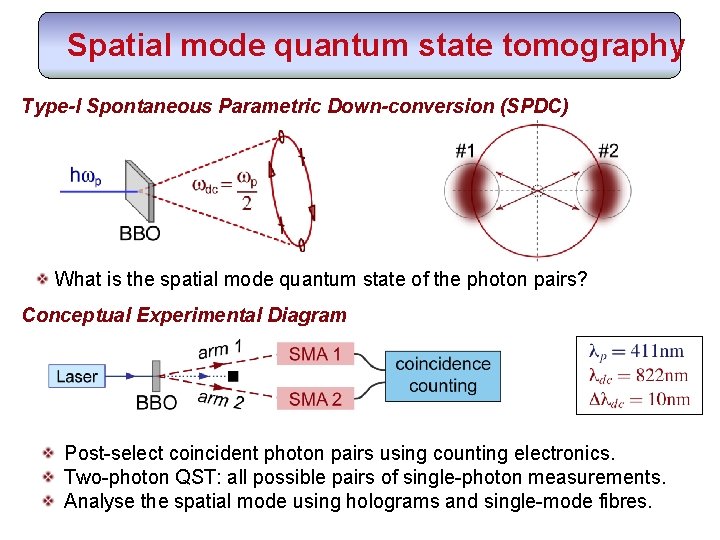
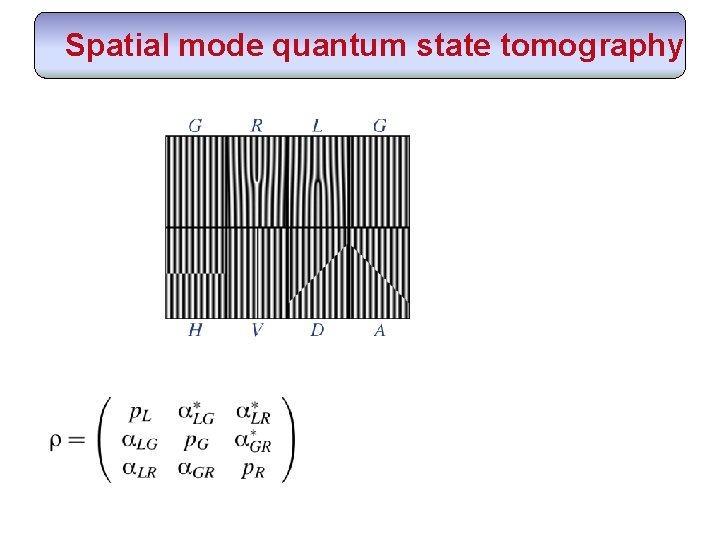
Spatial mode quantum state tomography Type-I Spontaneous Parametric Down-conversion (SPDC) What is the spatial mode quantum state of the photon pairs? Conceptual Experimental Diagram Post-select coincident photon pairs using counting electronics. Two-photon QST: all possible pairs of single-photon measurements. Analyse the spatial mode using holograms and single-mode fibres.
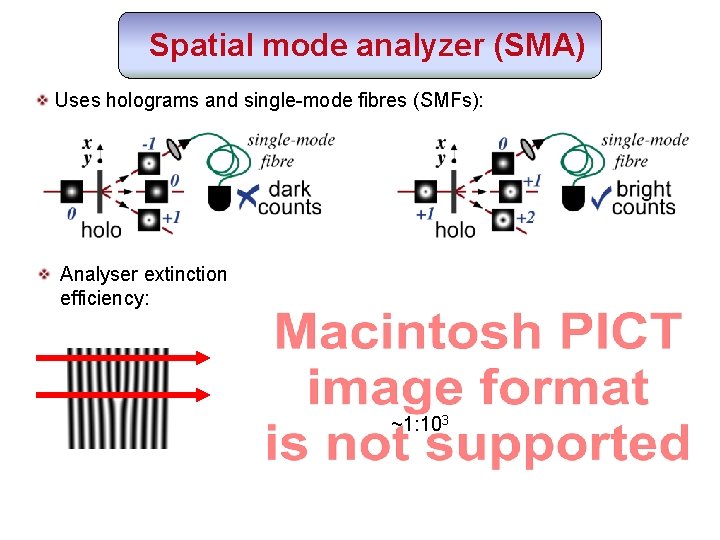
Spatial mode analyzer (SMA) Uses holograms and single-mode fibres (SMFs): Analyser extinction efficiency: ~1: 103
Spatial mode quantum state tomography
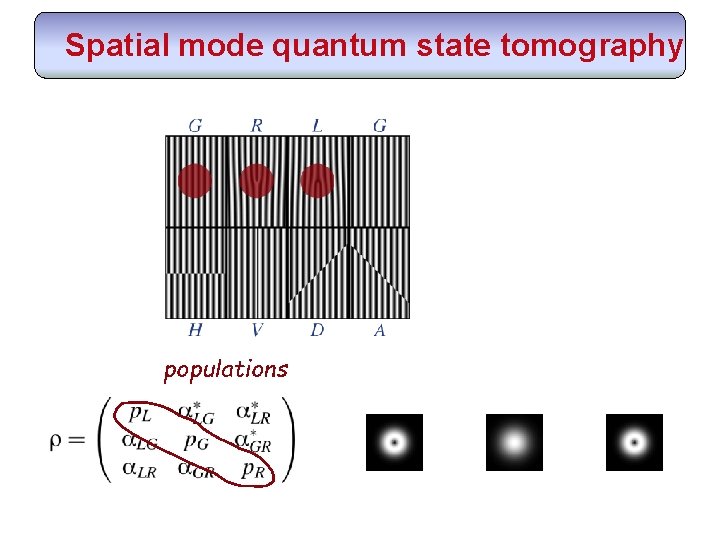
Spatial mode quantum state tomography populations
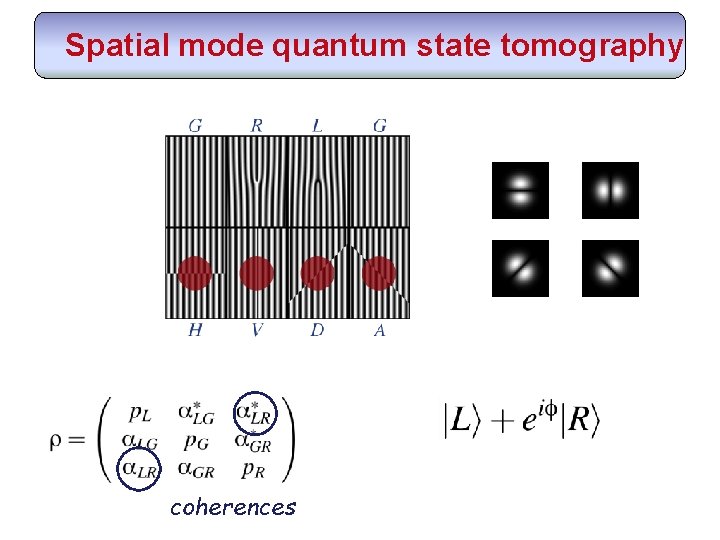
Spatial mode quantum state tomography coherences
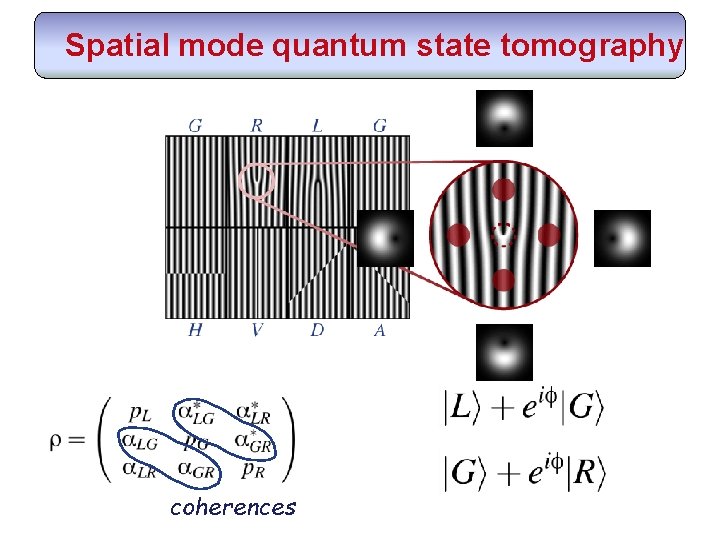
Spatial mode quantum state tomography coherences
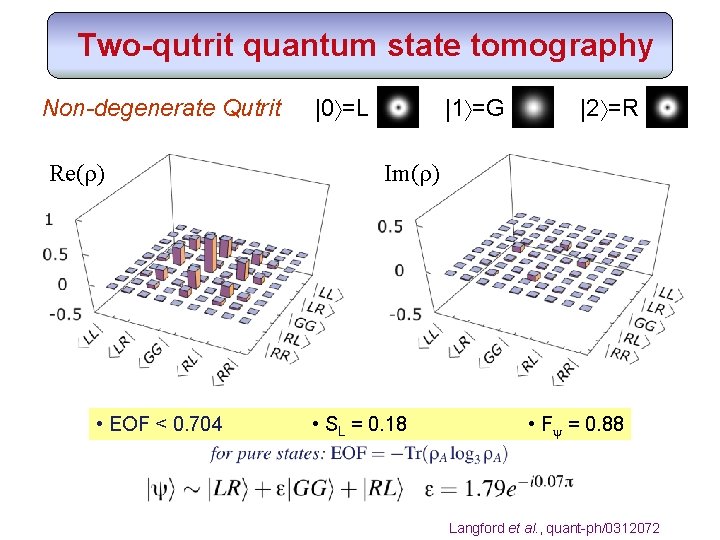
Two-qutrit quantum state tomography Non-degenerate Qutrit Re(r) • EOF < 0. 704 |0 =L |1 =G |2 =R Im(r) • SL = 0. 18 • Fy = 0. 88 Langford et al. , quant-ph/0312072
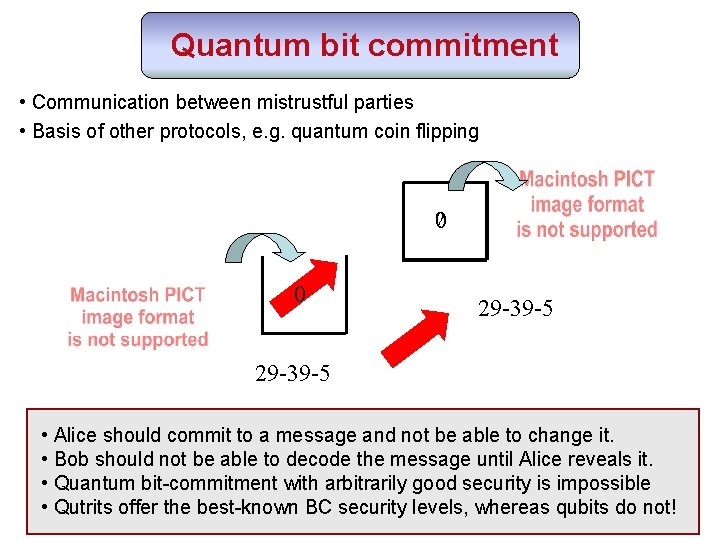
Quantum bit commitment • Communication between mistrustful parties • Basis of other protocols, e. g. quantum coin flipping 0? 0 29 -39 -5 • Alice should commit to a message and not be able to change it. • Bob should not be able to decode the message until Alice reveals it. • Quantum bit-commitment with arbitrarily good security is impossible • Qutrits offer the best-known BC security levels, whereas qubits do not!
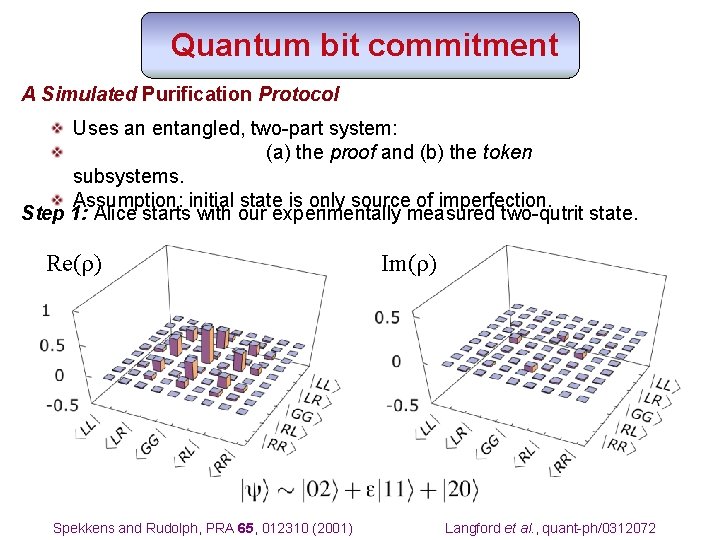
Quantum bit commitment A Simulated Purification Protocol Uses an entangled, two-part system: (a) the proof and (b) the token subsystems. Assumption: initial state is only source of imperfection. Step 1: Alice starts with our experimentally measured two-qutrit state. Re(r) Spekkens and Rudolph, PRA 65, 012310 (2001) Im(r) Langford et al. , quant-ph/0312072
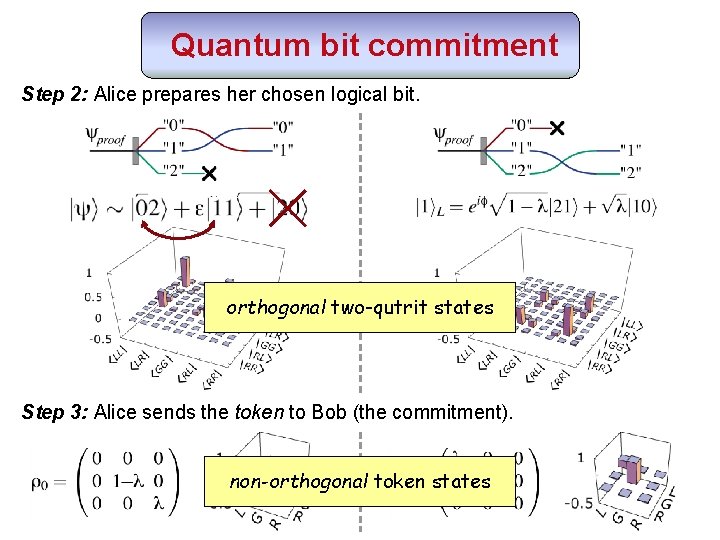
Quantum bit commitment Step 2: Alice prepares her chosen logical bit. orthogonal two-qutrit states Step 3: Alice sends the token to Bob (the commitment). non-orthogonal token states

Quantum bit commitment Step 4: Alice sends the proof subsystem to Bob to complete the BC protocol. He decodes the message with a two-qutrit projective measurement: Distinguishability of token states limits Alice’s control (trace-distance): Non-orthogonal token states limit Bob’s possible knowledge gain (fidelity):
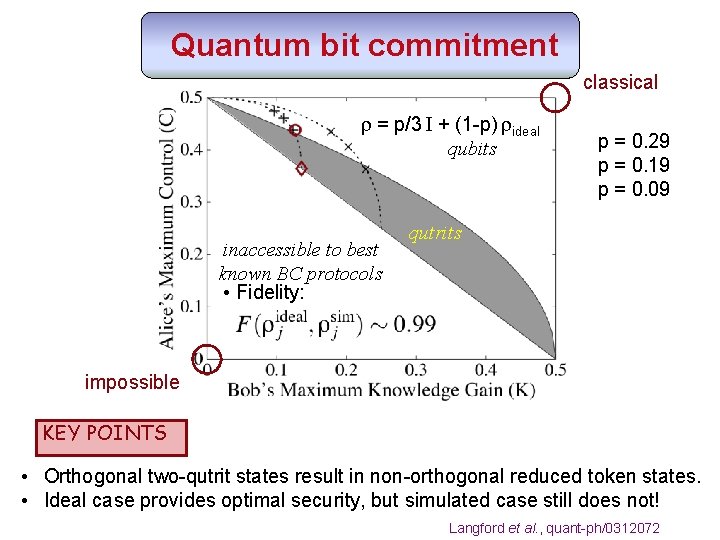
Quantum bit commitment classical achievable r = p/3 rideal I + (1 -p) with qubits inaccessible to best known BC protocols • Fidelity: p = 0. 29 p = 0. 19 p = 0. 09 qutrits impossible KEY POINTS • Orthogonal two-qutrit states result in non-orthogonal reduced token states. • Ideal case provides optimal security, but simulated case still does not! Langford et al. , quant-ph/0312072

Conclusions • Quantum process tomography of CNOT – fully characterize the process in the 2 -qubit space – high fidelity operation useful for q. info and q. physics tests • Generalized measurement and QND – non-destructive; arbitrary strength; any basis • Qutrit entanglement – measured, characterized for use in communications protocols
- Slides: 47