Generalizing Plans to New Environments in Multiagent Relational

Generalizing Plans to New Environments in Multiagent Relational MDPs Carlos Guestrin Daphne Koller Stanford University

Multiagent Coordination Examples n n n Search and rescue Factory management Supply chain Firefighting Network routing Air traffic control n n Multiple, simultaneous decisions Exponentially-large spaces Limited observability Limited communication

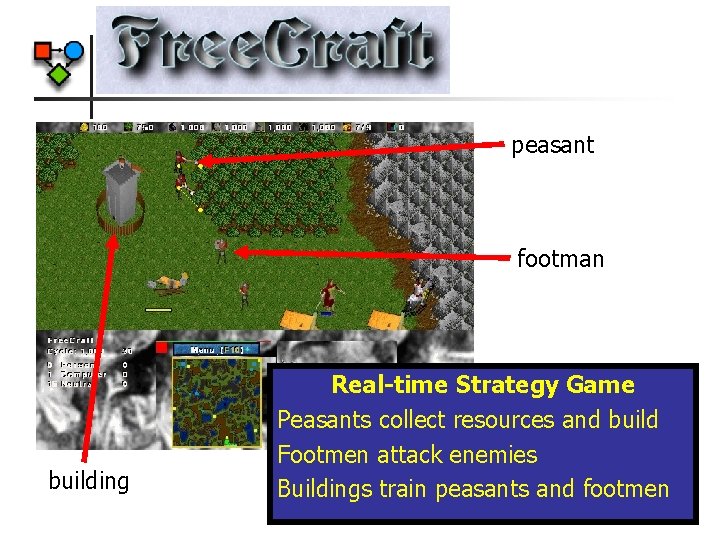
peasant footman building Real-time Strategy Game Peasants collect resources and build Footmen attack enemies Buildings train peasants and footmen

Scaling up by Generalization n n Exploit similarities between world elements Generalize plans: n n n From a set of worlds to a new, unseen world Avoid need to replan Tackle larger problems Formalize notion of “similar” elements Compute generalizable plans

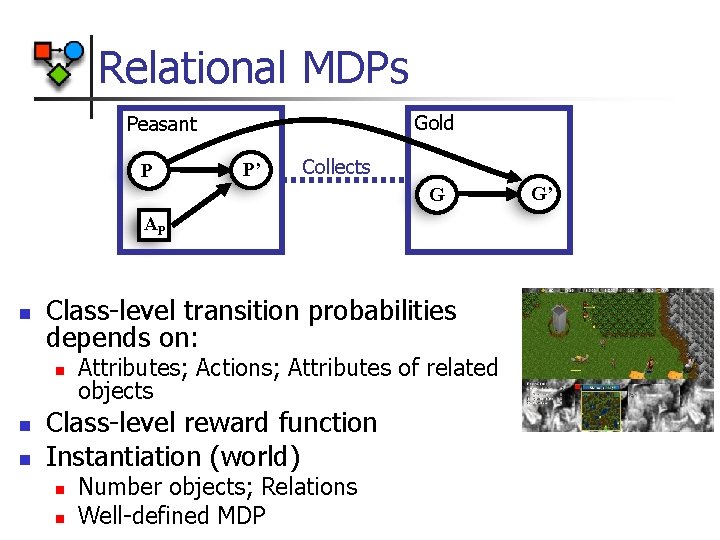
Relational Models and MDPs n Classes: n n Relations n n Peasant 1, Peasant 2, Footman 1, Enemy 1… Value functions in class level n n Collects, Builds, Trains, Attacks… Instances n n Peasant, Gold, Wood, Barracks, Footman, Enemy… Objects of the same class have same contribution to value function Factored MDP equivalents of PRMs [Koller, Pfeffer ‘ 98]

Relational MDPs Gold Peasant P P’ Collects G AP n Class-level transition probabilities depends on: n n n Attributes; Actions; Attributes of related objects Class-level reward function Instantiation (world) n n Number objects; Relations Well-defined MDP G’

Planning in a World n Long-term planning by solving MDP n n # states exponential in number of objects # actions exponential Efficient approximation by exploiting structure! RMDP world is a factored MDP

Roadmap to Generalization n Solve 1 world n Compute generalizable value function n Tackle a new world

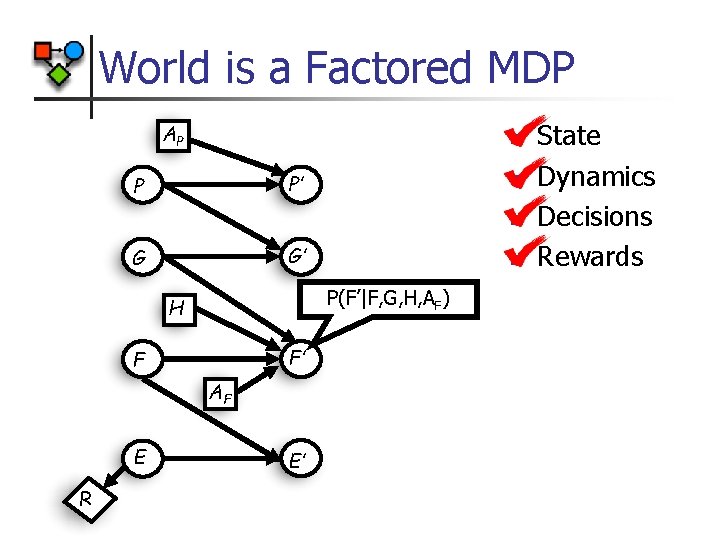
World is a Factored MDP AP n P’ P n n G’ G P(F’|F, G, H, AF) H F’ F AF E R n E’ State Dynamics Decisions Rewards

Long-term Utility = Value of MDP n n Value computed by linear programming: [Manne `60] One variable V (x) for each state One constraint for each state x and action a Number of states and actions exponential!

Approximate Value Functions Linear combination of restricted domain functions [Bellman et al. `63] [Tsitsiklis & Van Roy `96] [Koller & Parr `99, `00] [Guestrin et al. `01] n Each Vo depends on state of object and related objects: n n n State of footman Status of barracks Must find Vo giving good approximate value function

Single LP Solution for Factored MDPs [Schweitzer and Seidmann ‘ 85] n Variables for each Vo , for each object n n One constraint for every state and action n n Polynomially many LP variables Exponentially many LP constraints Vo , Qo depend on small sets of variables/actions n Exploit structure as in variable elimination [Guestrin, Koller, Parr `01]

Representing Exponentially Many Constraints Exponentially many linear = one nonlinear constraint

Variable Elimination n Can use variable elimination to maximize over state space: [Bertele & Brioschi ‘ 72] max f 1 ( A, B) + f 2 ( A, C ) + f 3 (C , D) + f 4 ( B, D) A A, B , C , D = max f 1 ( A, B) + f 2 ( A, C ) + max[f 3 (C , D) + f 4 ( B, D) ] A, B , C D = max f 1 ( A, B) + f 2 ( A, C ) + g 1 ( B, C ) B C A, B , C D Here we need only 23, instead of 63 sum operations n As in Bayes nets, maximization is exponential in tree-width

Representing the Constraints n Functions are factored, use Variable Elimination to represent constraints: Number of constraints exponentially smaller

Roadmap to Generalization n Solve 1 world n Compute generalizable value function n Tackle a new world

Generalization n Sample a set of worlds n Solve a linear program for these worlds: n n Obtain class value functions When faced with new problem: n n Use class value function No re-planning needed

Worlds and RMDPs n Meta-level MDP: n Meta-level LP:

Class-level Value Functions n n Approximate solution to meta-level MDP Linear approximation Value function defined in the class level All instances use same local value function

Class-level LP n n n Constraints for each world represented by factored LP Number of worlds exponential or infinite Sample worlds from P( )

Theorem Exponentially (infinitely) many worlds ! need exponentially many samples? NO! samples Value function within , with prob. at least 1 -. Rmax is the maximum class reward Proof method related to [de Farias, Van Roy ‘ 02]

LP with sampled worlds n n Solve LP for sampled worlds Use Factored LP for each world Obtain class-level value function New world: instantiate value function and act

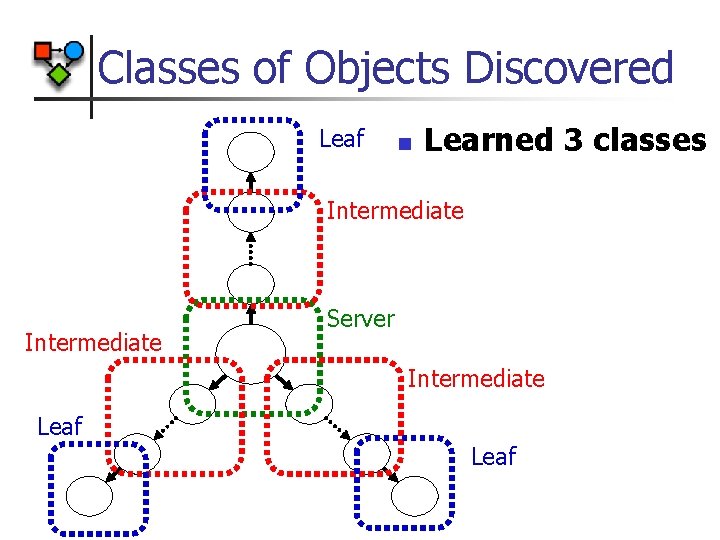
Learning Classes of Objects n Which classes of objects have same value function? n Plan for sampled worlds individually Use value function as “training data” Find objects with similar values Include features of world n Used decision tree regression in experiments n n n

Summary of Generalization Algorithm 1. Model domain as Relational MDPs 2. Pick local object value functions Vo 3. Learn classes by solving some instances 4. Sample set of worlds 5. Factored LP computes class-level value function

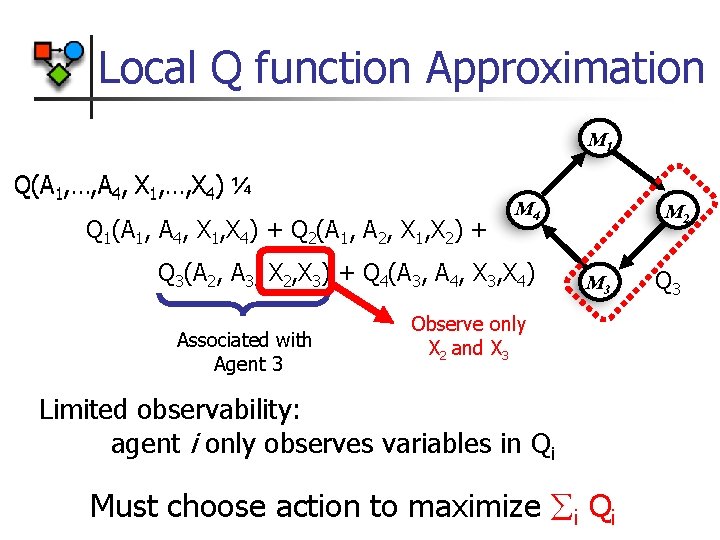
A New World n When faced with a new world , value function is: n Q function becomes: n n n At each state, choose action maximizing Q(x, a) Number of actions is exponential! Each QC depends only on a few objects!!!

Local Q function Approximation M 1 Q(A 1, …, A 4, X 1, …, X 4) ¼ Q 1(A 1, A 4, X 1, X 4) + Q 2(A 1, A 2, X 1, X 2) + M 4 Q 3(A 2, A 3, X 2, X 3) + Q 4(A 3, A 4, X 3, X 4) Associated with Agent 3 M 2 M 3 Observe only X 2 and X 3 Limited observability: agent i only observes variables in Qi Must choose action to maximize åi Qi Q 3

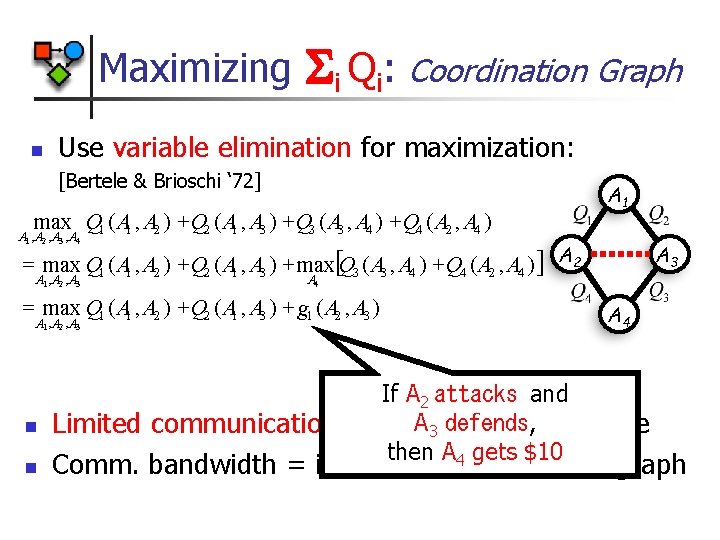
Maximizing n i Qi: Coordination Graph Use variable elimination for maximization: [Bertele & Brioschi ‘ 72] max Q 1 ( A 1 , A 2 ) + Q 2 ( A 1 , A 3 ) + Q 3 ( A 3 , A 4 ) + Q 4 ( A 2 , A 4 ) A 1 , A 2 , A 3 , A 4 = max Q 1 ( A 1 , A 2 ) + Q 2 ( A 1 , A 3 ) + max[Q 3 ( A 3 , A 4 ) + Q 4 ( A 2 , A 4 ) ] A 2 A 1 , A 2 , A 3 A 4 = max Q 1 ( A 1 , A 2 ) + Q 2 ( A 1 , A 3 ) + g 1 ( A 2 , A 3 ) A 1 , A 2 , A 3 n n A 3 A 4 If A 2 attacks and A 3 defends, Limited communication for optimal action choice then A 4 gets $10 Comm. bandwidth = induced width of coord. graph

Summary of Algorithm 1. Model domain as Relational MDPs 2. Factored LP computes class-level value function 3. Reuse class-level value function in new world

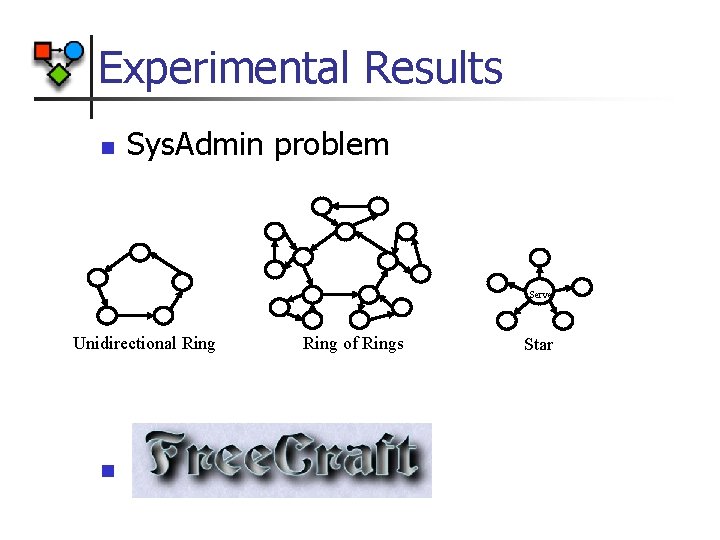
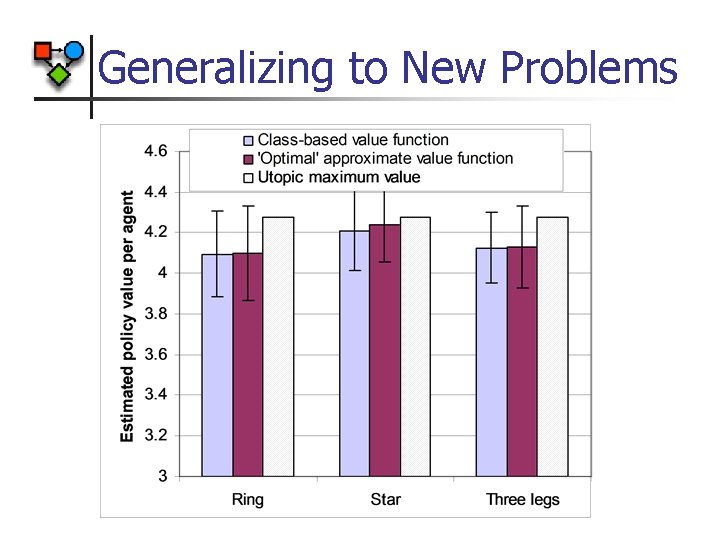
Experimental Results n Sys. Admin problem Server Unidirectional Ring n Ring of Rings Star

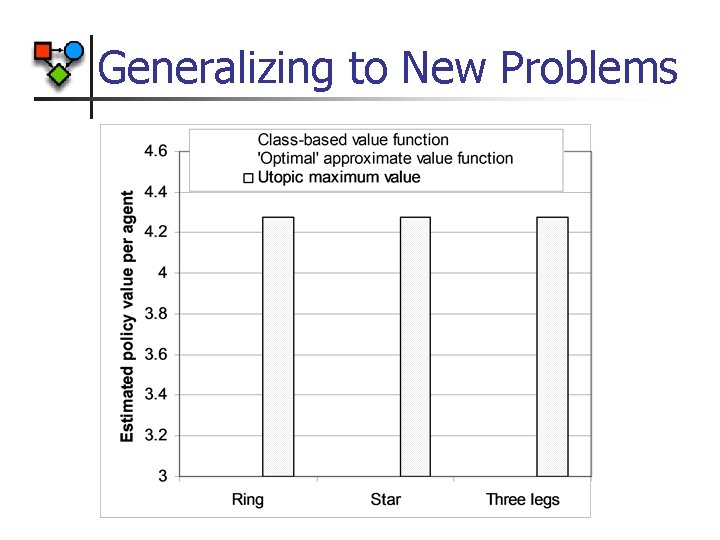
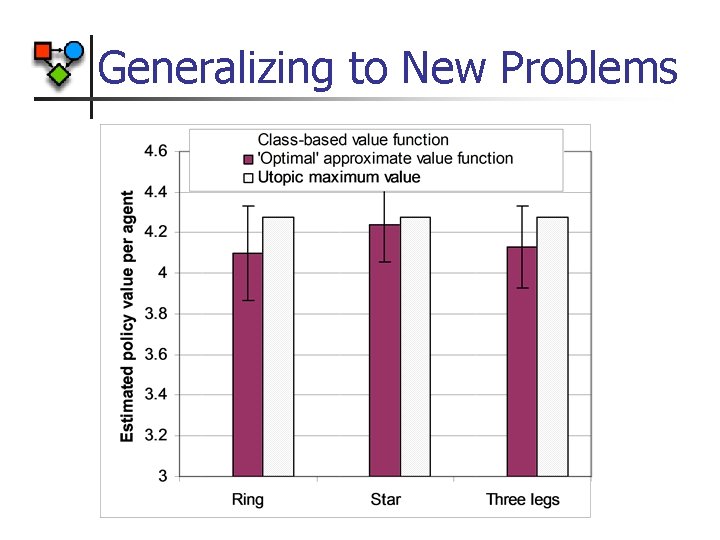
Generalizing to New Problems

Generalizing to New Problems

Generalizing to New Problems

Classes of Objects Discovered Leaf n Learned 3 classes Intermediate Server Intermediate Leaf

Learning Classes of Objects

Learning Classes of Objects

Results n 2 Peasants, Gold, Wood, Barracks, 2 Footman, Enemy [with Gearhart and Kanodia] n Reward for dead enemy n About 1 million of state/action pairs n Solve with Factored LP n Some factors are exponential n Coordination graph for action selection

Generalization n 9 Peasants, Gold, Wood, Barracks, 3 Footman, Enemy n Reward for dead enemy n About 3 trillion of state/action pairs n Instantiate generalizable value function n At run-time, factors are polynomial n Coordination graph for action selection

The 3 aspects of this talk n Scaling up collaborative multiagent planning n n n Factored representation and algorithms n n Exploiting structure Generalization Relational MDP, Factored LP, coordination graph Freecraft as a benchmark domain

Conclusions n RMDP n Compact representation for set of similar planning problems n Solve single instance with factored MDP algorithms Tackle sets of problems with class-level value functions Efficient sampling of worlds Learn classes of value functions n Generalization to new domains n n n Avoid replanning Solve larger, more complex MDPs